浅谈数学分析中极限的求法

马金玲 (吉林师范大学，吉林 长春 130000)

在数学分析的学习中，我们发现数列和函数极限的形式很复杂，因此,求解极限的方法也多种多样，当然，对于不同的方法有其各自的优势及适用范围.本文通过对典型例题的探究求解，归纳总结出一些常用的求解方法，以探究数学中的技巧性，提升学生对数学知识体系的梳理能力.另外，本文旨在通过应用无穷小量、重要极限、洛必达法则等方法，在求解极限的过程中体会数学思维的转化，感受数学知识的紧密联系，构建条理清晰、逻辑严谨的数学知识框架.

一、极限的定义

数列极限的ε—N定义设{an}为数列，a为定数.若对任给的正数ε，总存在正整数N，使得当n>N时有

|an-a|<ε，

则称数列{an}收敛于a，定数a称为数列{an}的极限，并记作

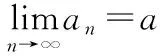
函数极限的ε—δ定义设函数f在点x0的某个空心邻域U°(x0；δ′)内有定义，A为定数.若对任给的ε>0，存在正数δ(<δ′)，使得当0<|x-x0|<δ时有

|f(x)-A|<ε，

则称函数f当x趋于x0时以A为极限，记作

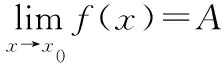
二、极限的求解

1.单调有界定理

定理1在实数域中，若数列{an}单调且有界，则数列{an}一定存在极限.

注(1)在应用单调有界定理求解极限时，首先要满足数列{an}是单调数列，即满足an≤an+1(或an≥an+1)，其次要保证数列{an}有界.

(2)证{an}的单调性：

① 考察an+1-an的符号；

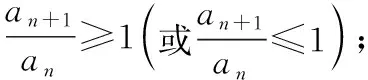
③ 若得到一个一元可导函数的递推公式an+1=f(an)，则可求导，然后根据f′(x)的符号来确定其单调性.

证{an}的有界性常利用数学归纳法或已知不等式推证.

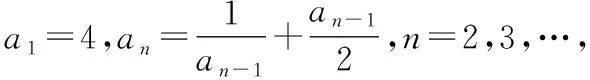
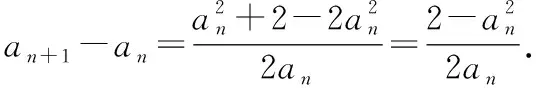
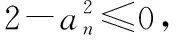
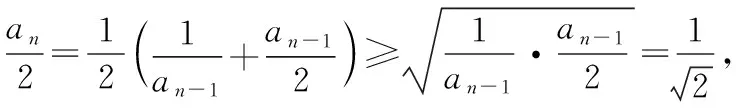
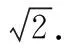
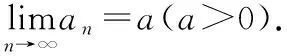
归纳小结在应用单调有界定理求解数列极限时，首先要证明的是数列存在极限，也就要证明数列满足单调性和有界性.证明单调性的过程考查了学生对初等数学中数列知识的掌握，其证明方法的选用要根据具体问题而定；而在证明有界性时常应用数学归纳法.在证明极限存在时应分两步走，且将高等数学的问题转化为初等数学的知识，让难题迎刃而解，最后依据极限的唯一性求出极限值.值得注意的是，单调有界定理只适用于满足条件的数列求解极限问题.

2.迫敛性

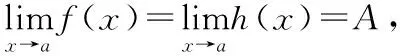
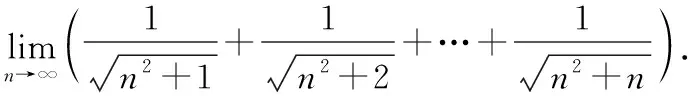
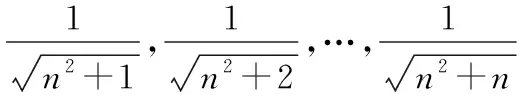
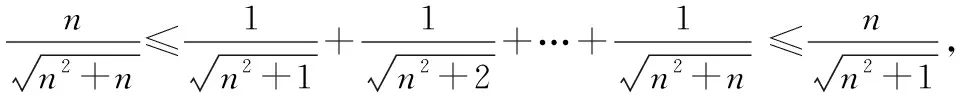
所以，由迫敛性得

归纳小结在应用迫敛性求解数列或函数极限时，可将对极限的直接求解转化为先对极限变量进行放缩，再找出易求得极限的上下界，从而间接求得原极限.值得注意的是，在遇到极限变量可以进行放缩的求解极限问题时可以优先考虑迫敛性.

3.两个重要极限

注在应用重要极限求解极限时，首先要进行初等变形.这里的初等变形是指用初等数学的方法将数列或函数转化成上述两个重要极限的形式.

解将原式中的函数凑成如下形式，

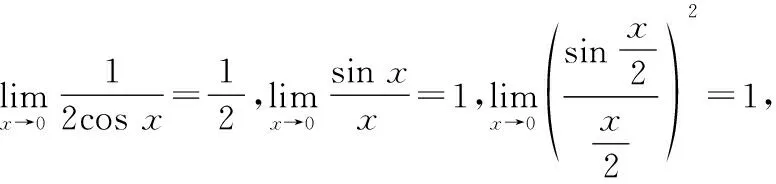
于是有

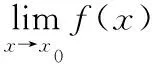
注归结原则在数列(离散变量)极限与函数(连续变量)极限之间建立起了桥梁，使二者在一定条件下可以相互转化，这对处理极限问题起到了重要的作用.

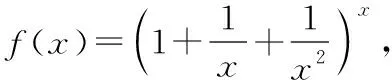
由归结原则，得

归纳小结在应用两个重要极限求解极限问题时，首先要应用初等数学的方法将数列或函数化成两个重要极限的形式之一，再进行求解.应用该方法的关键就在于将原极限形式“凑成”上述两个重要极限.值得注意的是，在遇到三角函数形式和“1∞”形式的极限问题时要优先考虑应用两个重要极限.另外，在求解“1∞”形式的数列极限时，要结合归结原则将数列问题转化成函数问题，再进行求解.

4.洛必达法则

洛必达法则是求不定式极限的重要方法，它将两函数之比的极限求解问题转化为两函数导数之比的极限求解问题.其几何意义是：两曲线上的点的纵坐标之比的极限可转化为两曲线上的点的切线斜率之比的极限.

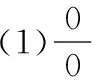
定理3若函数f(x)与g(x)满足条件：

(ⅱ)在点x0的某空心邻域U°(x0)上，f(x)与g(x)都可导，且g′(x)≠0；

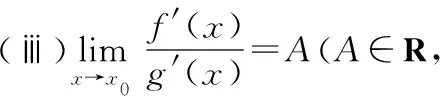
则

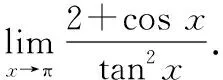
故由洛必达法则求得

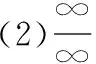
定理4若函数f(x)与g(x)满足条件：

(ⅰ)在U°+(x0)上二者皆可导，且g′(x)≠0；

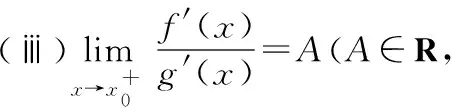
则

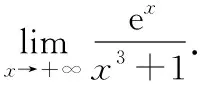
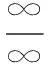
归纳小结应用洛必达法则求解极限问题，其实质在于将求解两个函数之比的极限转化为两函数导数之比的极限，使得复杂函数的求极限问题转化为简单函数的求极限问题.但在应用洛必达法则时有些需要注意的问题：

(1)不是所有比式极限都可以应用洛必达法则求解，一方面必须注意它是不是不定式极限，另一方面要看是否满足洛必达法则的应用条件；

(2)在求解极限的过程中，有时可能需要对f′(x)与g′(x)再应用洛必达法则，甚至有时需要对f(x)与g(x)的高阶导数反复使用洛必达法则.

5.定积分

利用定积分求极限，通常有两种类型：一种是应用定积分的定义求解数列极限，另一种是应用变限积分和洛必达法则求解极限.

(1)用定积分定义求解数列极限

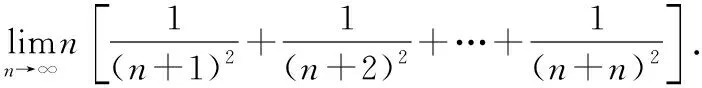
解做如下变形：

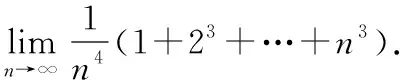
解做如下变形:

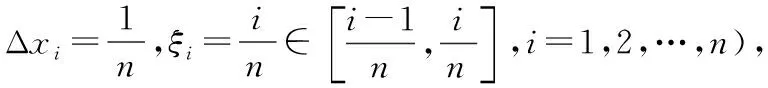
(2)应用变限积分求解极限

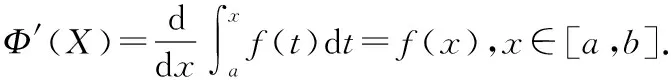
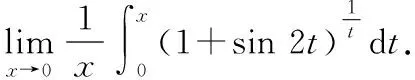
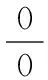
恒等变换后有

于是有

归纳小结应用变限积分求解极限的过程中，主要是将原函数存在定理与洛必达法则相结合，进而求得原极限.

三、结 语

本文主要介绍了求解极限的多种方法.在极限理论中，求解极限问题占据着重要地位，由于极限的类型复杂繁多，我们根据对典型例题的探究，归纳总结了求解极限不同方法的适用条件及其中所蕴含的转化思想.因此，在面对极限求解问题时，我们首先要判断所求极限的类型，再选取合适的方法进行求解.当然，在选择方法时，要注意其适用条件，这一过程是非常重要的，否则会得出错误的结论.另外，在求解极限的过程中，数学思维的多样转化也让我们体会到了数学知识之间的紧密联系，从而建立了逻辑清晰的数学知识体系.