箱梁截面测点实测温度分析及相关温度场构建
■陈 标
(福建省交通科研院有限公司,福州 350004)
1 工程概况
该现浇箱梁为全预应力混凝土结构,桥面净宽15.75 m,单箱双室截面。 墩顶0 号梁段长14.0 m,连续刚构主墩对应的2 个“T 构”的悬臂各分为20 对梁段,其梁段数及梁段长度从根部至跨中各为:13×3 m、7×4 m, 累计悬臂总长73 m。 跨中合拢段为2 m, 边跨现浇梁段长7.88 m。 主墩墩顶处箱梁高9.2 m,跨中梁高3.5 m,箱梁高度按1.8 次抛物线变化;箱梁顶板厚为28 cm;主墩墩顶箱梁底板厚为105 cm, 跨中箱梁底板厚32 cm, 箱梁底板厚按1.8 次抛物线变化;腹板厚度:主墩墩顶0 号梁段及1~13 号梁段为75 cm,14 号梁段由75 cm 线性变化至50 cm,15~20 梁段及边跨现浇段为50 cm。
《机·智》一书的第一作者朱铎先认为,尽管现在设备通信协议的走向是趋于标准化,但是在利益格局的羁绊下,各大巨头之间尚未达成一致。总体上,德国的工业设备集成,偏向采用OPC UA协议,而北美和日本则更偏爱MTConnect协议。无论如何,不弄懂弄通这5000多种设备通信协议,设备互联就会受到极大的限制。
2 箱梁测点布置
如图1、2 所示, 本次试验中布置1# 截面与2#截面传感器, 分别埋设在预应力混凝土箱梁的顶板、腹板、底板,并将传感器与自动化网络综合测量采集箱连接。 其中,本文主要分析1# 截面测点,其温度测点布置如图3 所示。

图1 1#、2# 测点截面顺桥向示意图
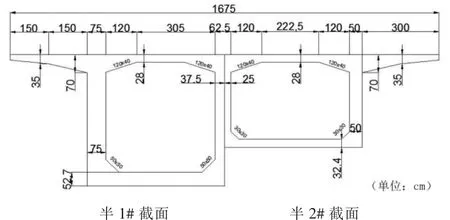
图2 1#、2# 箱梁截面构造图

图3 1# 截面温度测点布置图
3 梁截面测点实测温度分析及温度场构建
一般情况下,当太阳辐射较大时会使得混凝土箱梁出现最不利温度梯度分布,故本节选取了6 月28 日至7 月1 日共计4 天的温度数据展开研究。
2年区试与生产试验结果采用DPS数据统计软件[4],对黔糯优11的全生育期、有效穗、株高、穗长、穗粒数、实粒数、结实率、千粒重主要农艺性状和产量构成因素与产量进行相关性分析。
3.1 箱梁顶板测点实测温度分析
3.4.1 T0求值过程
3.4.2 指数a 计算
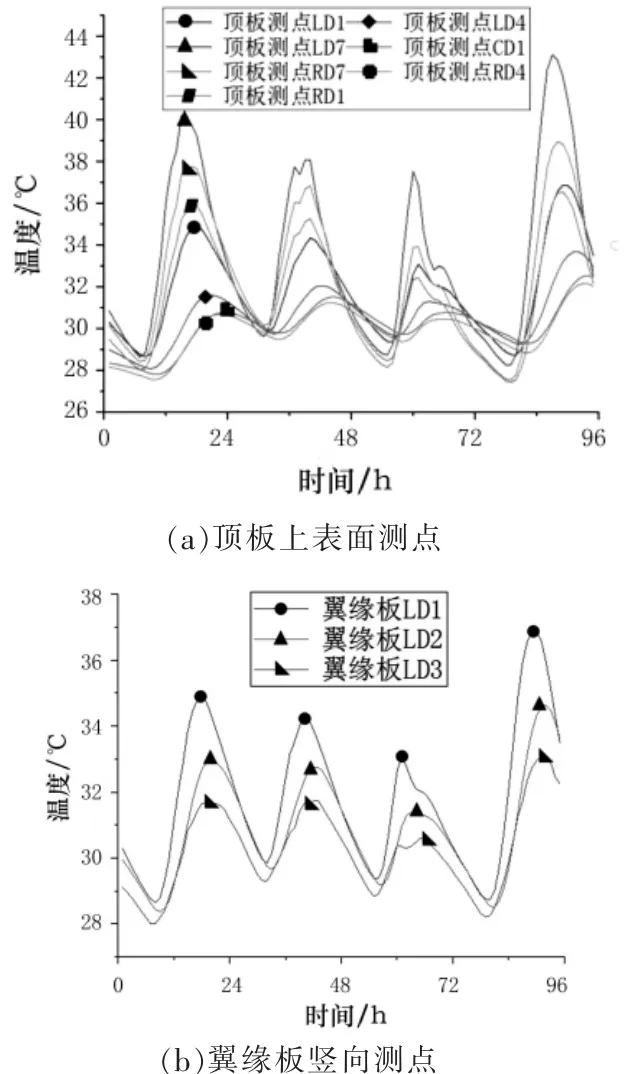
图4 箱梁顶板不同部位测点温度时程图
3.2 箱梁腹板测点实测温度分析
根据式(2),把T0当作独立的随机变量,以50年作为温度作用的重现期,根据计算的广义极值分布函数,得到日最大温差的极值为16.91℃。 但实际上T0不是独立的随机变量,进而考虑T0的相关性,即考虑极值指标θ=0.24,可得极值分布下的极限值为11.70℃。

图5 箱梁腹板不同部位测点温度时程图
3.3 箱梁底板测点实测温度分析
从图6 中可以看出:(1)底板下表面测点温度时程曲线呈现周期性变化,周期为24 h;(2)测点RB1 的温度在0-6 时下降明显,随后温度以较快的速率上升,受到的太阳辐射越大,其温度越高;测点CB1 由于位于截面中间位置,不受太阳辐射作用的直接影响,因此温度变化平缓,温度较低;测点LB1温度变化和RB1 相似, 但其温度峰值较RB1 测点小;(3)底板测点的横向温度差较小,最大处也仅为4℃左右,这是由于底板受太阳辐射作用影响小,主要影响其测点温度变化的因素为箱梁周围的大气温度变化及箱梁混凝土的导热作用,但相较于太阳辐射的直接作用,该影响效果十分有限。

图6 箱梁底板测点实测温度时程图
3.4 混凝土箱梁温度梯度的统计分析
通过在现场布置温度测点,自动采集系统经过采集、保存、传输等过程获得大量连续的箱梁实测温度数据,经过处理得到所有采集日期内每日温度梯度的最大温差值,如表1 所示。 将其结果绘制在一张散点图上,得到图7。

通过分析,由图4(a)可知:(1)箱梁顶板上表面测点温度变化具有周期性;(2)腹板顶面3 个测点(LD4、CD1、RD4)温度变化规律几乎一致;2 个箱室顶部测点(LD7、RD7)和两侧翼缘板顶面测点(LD1、RD1)温度变化规律几乎相同,其中两侧翼缘板顶面测点温度较高, 且以LD7 测点的温度为最高,其原因一方面是由于翼缘板处测点埋置深度较浅,另一方面是受太阳辐射角度的影响;(3)两箱室顶部测点及翼缘板顶面测点基本在相同时间到达一天内温度极大值, 即在16∶00-18∶00 间达到温度极大值,在06∶00-07∶00 间达到温度极小值;而腹板顶面测点达到极值时间相对滞后2 h。 由图4(b)可知:(1)翼缘板竖向测点温度变化具有周期性;(2)测点LD1 在测试期间温度变化相对较大,每日温度波动达到5℃左右, 这是因为其所处位置受太阳辐射作用显著;而其余两测点(LD2、LD3)由于太阳辐射角较小,温度变化相对平缓。
本文以某桥6-7 月份高温季节每天最大温度梯度为分析对象,根据极值统计理论,通过对实测数据的研究,得到较为准确的箱梁最不利温度梯度的表达式。 方志等[1]提出的指数曲线能对温度梯度进行较好的拟合,因此本文予以借鉴,采用式(1)的温度梯度曲线进行后续研究。

表1 最大温差统计数据汇总

图7 最大温差随时间的分布图
由图7 可知,在统计天数内,分析箱梁温度梯度的日最大温差值可知,其值在某一温度范围内发生随机波动,因此认为整组分析数据的概率分布满足随机变量的分布条件要求,进一步将该组随机样本数据按照一定的温度分布区间进行统计计算,求出各温度区间的概率分布情况,结果如图8所示。

图8 日最大温差分布直方图
为了更准确地确定指数a 的数值,选取更有参考价值的日最大温度差大于7℃的曲线作为样本数据,将其作为样本进行数据拟合,使用概率统计的方法求解指数a 的数值,统计分布结果如图11所示。
我国的畜牧兽医行业已经发展到了一个至关重要的时期,上级部门、基层部门、一线从业人员,都应该强化自己的责任意识。只有把责任放在心里,才能在工作中注意细节,注意质量。加强行业的执法监测力度,把畜牧产品的卫生、产品质量放到第一位,让安全成为畜牧兽医这行业的代名词。责任贵在落实,只有心中有责任,手上有落实,才能真正的为行业的创新改革保驾护航。

通过对求得的极值分布函数进行统计分析描述可以进一步验证该求得的分布函数的合理性,求得该分布的P-P 图和Q-Q 图(图9、10),可知所有点都在同一条直线周围以较小幅度变化,表明使用该极值分布统计方法来求出的极值分布函数,用以计算箱梁日最大温差是合理的。
通过分析,由图5(a)可知:(1)腹板测点LW4在一天内波动最为明显,且各点温度波动具有明显的周期性,周期为24 h;(2)测点RW4 温度波动规律与LW4 相同,但其温度波动幅值较小,且到达温度峰值的时间较晚;(3)考虑到测点CW2 布置于箱梁中间腹板上,其温度变化主要受混凝土导热作用影响,又由于混凝土箱室空间封闭,加之混凝土保温隔热作用的影响,因此导致该测点温度较为稳定且没有呈现出明显的周期性变化规律。 由图5(b)可知:腹板顶面测点LD4 温度最高,可接近34℃,而其他下部测点温差不明显,温差在1℃以内。因此腹板上部存在竖向温差,而中部温差较小。

图10 T0 的Q-Q 图
现代化高效的交通管理,亟需打破部门数据孤岛,整合交通大数据,综合制定智能化交通解决方案,建设统一的跨部门、跨系统的交通大数据共享平台,实现数据共享与交换,并对数据进行深度挖掘分析,拓展交通应用,唯有这样才能发挥出通州作为城市副中心的作用,真正实现中心区与副中心的资源共享.
基于极值统计方法对最大温差数据进行参数估计, 通过计算得到箱梁竖向温度梯度最大温差的各个参数值,进而求得其极值分布函数如式(2)所示。
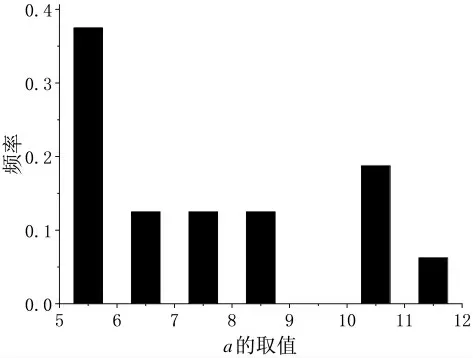
图11 a 的取值分布
由图11 可得, 指数a 取值主要分布在5~7 的区间范围,为了进一步简化求解最不利温度梯度曲线的表达式,忽略指数a 动态变化对求解的结果的影响, 本文在出现频率较大的分布范围基础上,选取其较大概率分布区间的中位数作为箱梁竖向最不利温度梯度曲线表达式的指数,即取指数为6。综上所述,由该桥温度实测数据得到,该桥的最不利温度梯度曲线如式(3)所示。

3.4.3 温度曲线对比
将计算曲线与既有研究结果及现行桥梁设计规范进行对比,考虑到实际的箱梁温度梯度分布形式为非线性分布,目前研究中主要参考铁路桥涵规范对箱梁温度梯度进行选取。
根据前文研究分析,得到了本桥的温度分布曲线函数为T=11.7e-6y。为了研究不同地区温度梯度曲线的差异, 选取了其他学者的箱梁温度梯度曲线的结果:如刘海弯[2]对陕西地区一座桥梁进行一年的观测,通过统计分析得到的温度梯度曲线T=20.43e-6y;陶翀[3]对位于浙江淳安县的一座大桥进行为期两年的观测, 获得其温度梯度曲线为T=17.83e-3y;按照《铁路桥涵设计规范》[4]的规定,可得箱梁温度梯度曲线为T=20e-5y。 各温度梯度曲线如图12 所示。
记录两种诊断方式的检查结果,并与最终手术治疗结果进行对比,统计两种方式的误诊、漏诊人数,以此计算各诊断方式的诊断准确率;记录两种诊断方式检查得出的突出征象,并与最终手术治疗结果进行对比,统计具体病因诊断的准确率。

图12 相关文献中的温度梯度曲线对比
由图12 可知, 各个地区的温度曲线均与规范中规定的温度曲线存在差异,并且各个不同地区之间温度梯度曲线也不尽相同,因此规范中对温度梯度曲线的规定不能完全符合各个地区的实际情况,应根据对箱梁的实测数据分析,求得准确的温度梯度曲线。 本文研究为建立该地区的箱梁温度梯度曲线提供了大量实测数据和有价值的经验,研究得出的温度梯度曲线为我国建立更加全面、有效的箱梁温度梯度曲线提供了参考。
于是我们发现了自己的窘境:现在常常忧虑的不是知道得太少,而是知道得太多。各种信息太多了,什么网络小报广播电视杂志书籍——连风里都是各种各样的声音。我们的视听已经被严重堵塞,五官负担大大超载。这一切已经影响到我们的思考和判断,因为各种参照实在太多了。
4 结语
本文通过自动化云监测系统,建立智慧桥梁监测系统,对大桥进行长达数月的温度监测,获得了大量有效的实测数据。 利用极值统计的方法得到了箱梁截面竖向温度梯度曲线。 本文主要得到以下研究结论:(1)日照作用对箱梁温度场影响显著。 向阳侧腹板温度明显较背阳侧高。 腹板横向温度曲线近似呈现对称分布。 中间腹板由于混凝土保温隔热作用,温度变化较小。 腹板厚度方向尺寸对腹板横向温度曲线有一定影响,随着腹板厚度减小,温度差出现降低。 (2)通过极值统计分析方法对现场实测所得箱梁温度数据进行分析,确定了该桥温度梯度曲线表达式为T=11.7e-6y,经验证,该方法计算所得结果能较好地反应实测温度的统计特性。 通过对比不同地区的温度梯度曲线可知,温度梯度曲线的区域性差异较明显,规范中对温度梯度曲线的规定不能完全适用于各个地区,不同地区应考虑根据现场情况开展箱梁温度场的实测数据分析,求得准确的温度梯度曲线。

