商品条码实验室能力验证统计方法应用分析
郝元 张龄羽 胡敏/文
能力验证是通过实验室间比对,对参加者的能力进行评价的一种方式。周期性的开展检测能力验证,是维护与提升条码检测能力,掌握各检测机构条码检测能力、水平和环境的重要手段;同时也是评价条码检测结果的一致性,发现参加实验室中条码检测存在的问题,提高检测水平,确保实验室条码检测能力符合要求的有效方法;最后还是提高实验室检测数据的可信度,为不同实验室提供外部质量控制的有效手段。
能力验证评定与统计方法
选择不同的统计方法对能力验证的结果起至关重要的作用。能力验证数据统计的方法有很多种,目前比较常用的方法有中位值与标准化四分位距法和传统标准差法,本文针对这两种方法进行介绍,并且对其进行相互对比及分析。分析结果表明对于不同的能力验证项目以及不同的数据分布,需要考虑相关的标准和要求,选择合适的能力验证处理方法,否则会造成结果不准确、将“满意”结果误判成“不满意”等问题。
能力验证能力评定方法
常用的能力验证统计方法为Z比分数法,本文采用此方法对不同数据进行分析,其目的是依据能力评定准则将数据的偏离进行定量分析,且此统计方法不需要做任何处理与变换。Z比分数定量结果计算如下:
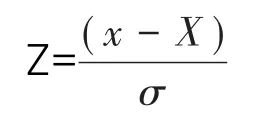
式中:Z为Z比分数值;x为参加能力验证实验室结果;X为数据指定值;σ为能力评定标准差。
使用Z比分数对参加实验室进行能力评定时,评定准则如下:
2<|Z|<3时,结果表明为“有问题”,产生警戒信号;
能力验证数据统计与分析方法
能力验证对数据的处理与分析提出了很大的挑战,虽然大多数数据分布都是近似于对称的单峰值数据,甚至近似于正态分布,但是能力验证数据大多都包含一定比例的偏离数据,造成此数据的原因有很多,例如在条码检测中,人员经验、设备长期未校准、设备校准方法错误、测试环境恶劣等都会造成数据偏移。所以选择可靠的统计方法将其剔除显得尤为重要。
中位值与标准化四分位距法
中位值与标准化四分位距法为稳健统计方法的一种简单算法,此方法中需要计算出数据的中位值与上下四分位值。中位值的物理意义表示为数据分布中间位置的一个估计,即一半数据高于它,一半数据低于它,并且在Z比分数计算时,中位值即为指定值。下四分位值Q1表示有四分之三数据高于它,四分之一数据低于它。上四分位值Q3表示有四分之一数据高于它,四分之三数据低于它。具体计算方法如下:
从某次检测中得到p个检测数据,将其按照递增的形式进行排列,表示为:X1,X2,X3,…Xi…Xp。计算其中位值,如下:

式中:med(x)为中位值。
此时计算四分位距(IQR)和标准化四分位距(NIQR),公式如下:
IQR=Q3-Q1
NIQR=0.7413×IQR
式中:Q1为下四分位值;Q3为上四分位值;
其中因数0.7413是从标准正态分布中计算得出。
传统标准差统计法
传统标准差统计法适用于接近于正态分布的数据分布,所以此方法对离群值较为敏感,如果不剔除离群值,将会对整体数据造成过大影响,所以在对数据处理之前需要用格拉布斯(Grubbs)检验法,检验与剔除明显离群值后,再进行数据分析。
因为离群值会对于平均值、标准偏差等参数造成过大的影响,所以在计算过程中需要首先判断数据是否离群,格拉布斯检验法如下所示:
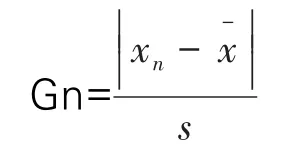
式中:xn为被验证数值;为样本平均值;s为样本标准差。
对于给定的显著性水平a和测出的数据数n,通过查看格拉布斯检验法临界值表得到临界值Ga,n,如果Gn>Ga,n,则此验证数值为离群值。
此时剔除离群值后的数据认为接近于正态分布数据,采用传统标准差统计法进行分析。此时在Z比分数计算中,样本平均值为指定值,样本的标准差为能力评定标准差。传统标准差具体计算方法如下:
从某次检测中得到p个检测数据,将其按照递增的形式进行排列,表示为:x1,x2,x3,…xi…xp。

以上两种方法均为比较简单直接的统计方法,两种方法的选择主要区别在于被处理数据的分布情况,例如中位值与标准化四分位距法中,因为计算中重要的数据为中位值和高低四分位值,离群值对其影响较小,所以此方法最明显的特点就是对离群值不敏感。而在传统标准差法中,计算中的重要数据为平均值、标准差,受离群值影响较大,所以在采用此方法时一般需要先剔除离群值后再计算。
综上,当数据分布接近正态分布的时候,两种方法都可以较为准确的处理数据;当数据分布非正态分布,并且分布过于集中时,则需要剔除离群值后选择传统标准差法。
应用实例
应用实例一
数据为A年条码检测能力验证中的可译码度数据,可译码度(decodability)为条码检测中条码符号与标准译码算法有关的各个单元或单元组合尺寸的可用容差中,未被印制偏差占用的部分与该单元或单元组合尺寸的可用容差之比的最小值,本文不做过多描述。
本次参加实验室数目为46个,参加本次能力验证的可译码度的数据与Z比分数,见表1,并且已进行由低到高排序处理,数据计算中的几个重要参数,见表2(下页)。
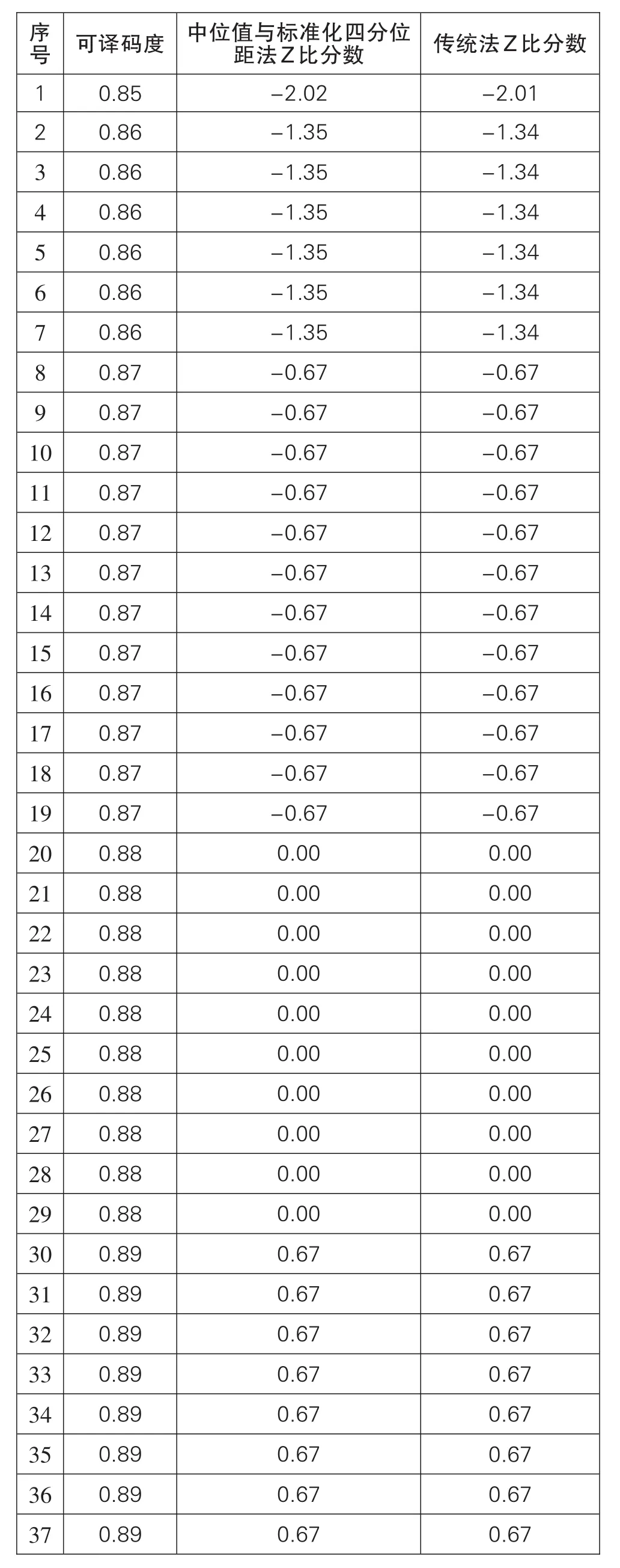
表1
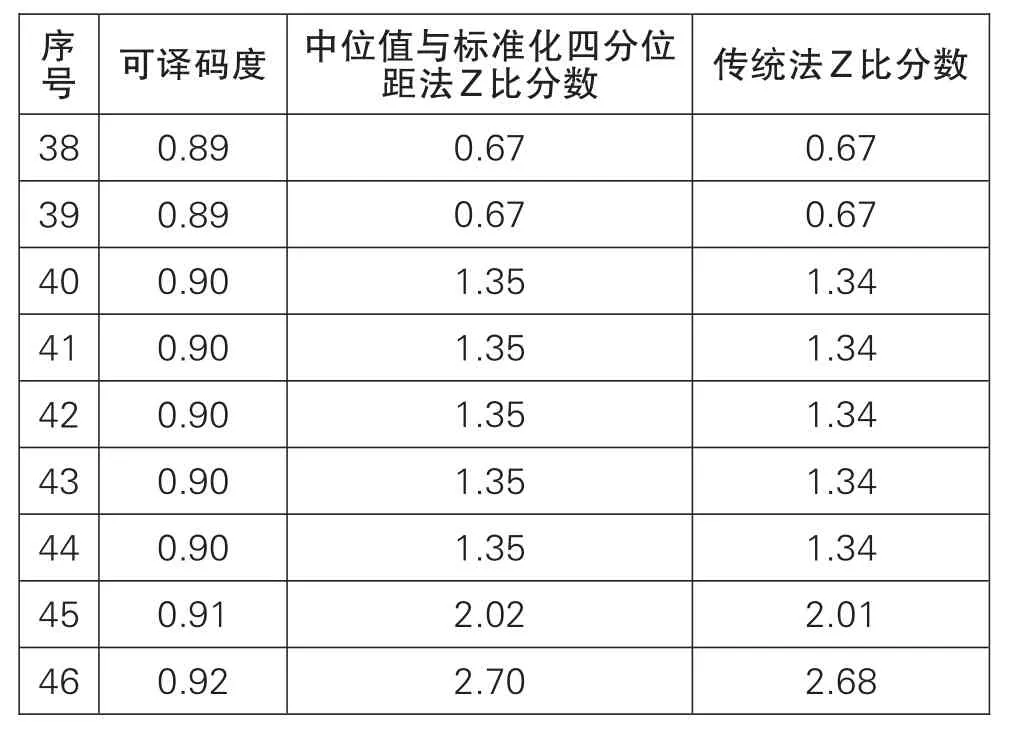
续
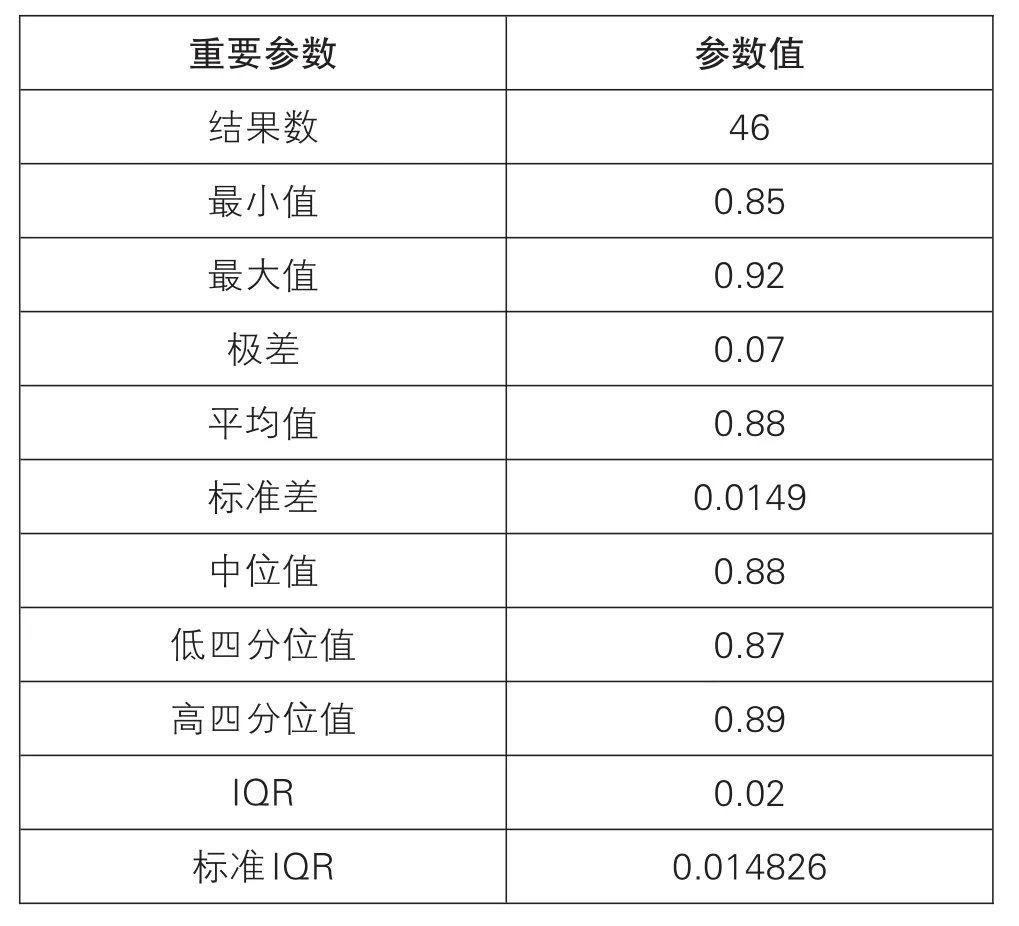
表2
数据分布为单个波峰的钟形曲线,并且从曲线图中观察无明显离群值,具体还需要通过离群值计算来判断是否存在离群值,如图1所示。由于数据总量不大,虽与正态分布曲线有所不同,但是总体分布曲线仍可近似于正态分布。
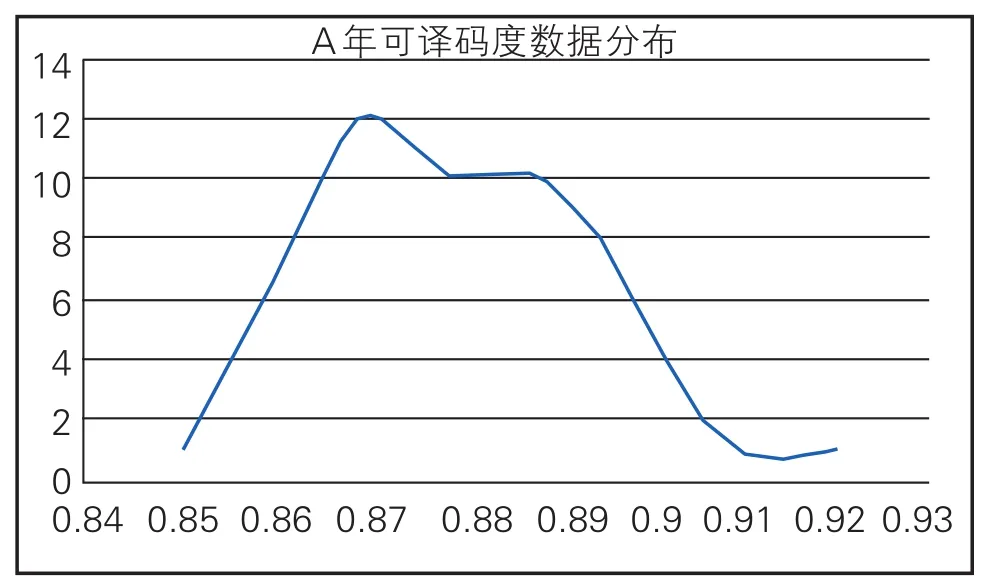
图1 A年可译码度数据分布
通过格拉布斯检验法可判断表1中数据无离群值,直接进行传统法进行数据处理。表1数据整体近似于正态分布,通过中位值与标准化四分位距法和传统标准差法计算出的Z比分数结果相近,数据中无“不满意”结果,序号为1、45、46的结果为“有问题”;最满意的结果为0.88,且0.88恰好为总数据的中位值,同时也为平均值;满意结果为2号到44号,结果值区间为0.86-0.90,满意结果区间相差0.04。此时无论选择中位值与标准化四分位距法还是传统标准差法均可以相对准确的计算出最满意结果值与不满意结果值。
应用实例二
数据为B年条码检测能力验证中的可译码度数据,见表3。本次参加实验室数目为47个,数据同时显示参加本次能力验证的可译码度的数据与Z比分数,并且已进行由低到高排序处理;数据计算中的几个重要参数,见表4(下页)。其中平均值与标准差均为剔除离群值后的结果。

表3
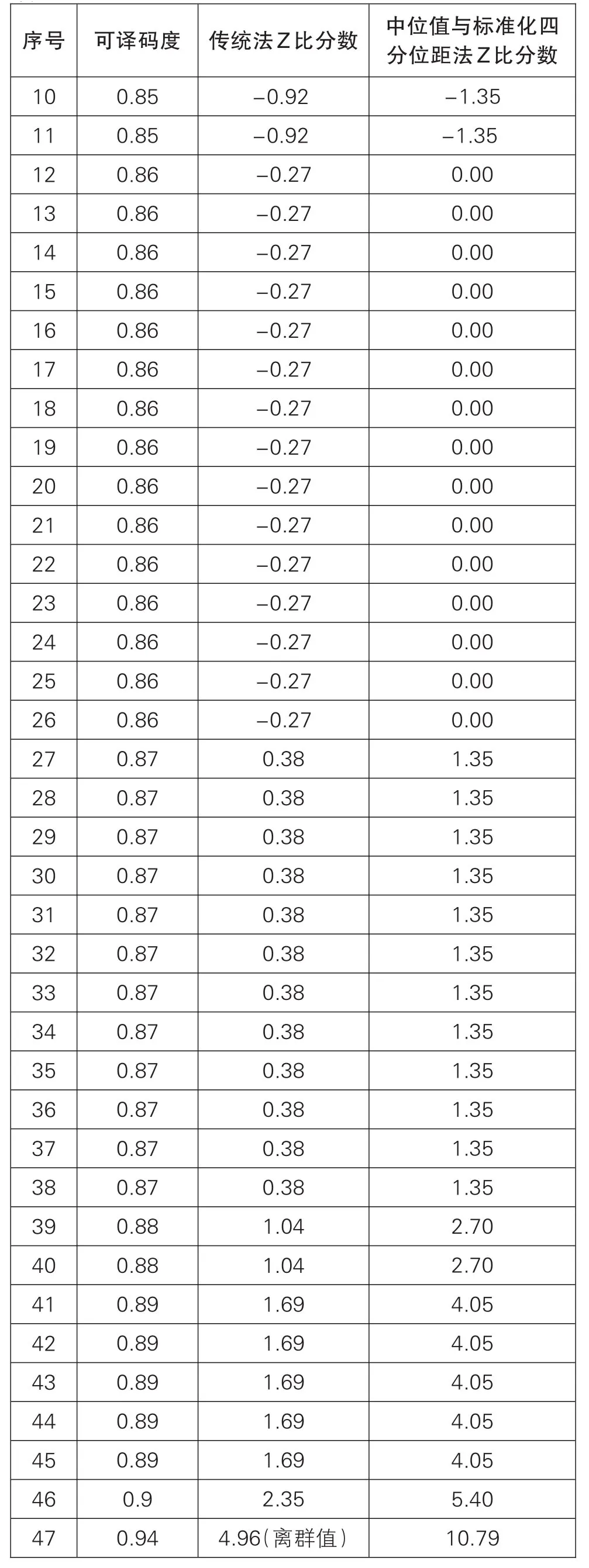
续

表4
数据分布为多个波峰的钟形曲线,且为0.86的数据过于集中,从曲线图中可观察到存在明显离群值,如图2所示。总体分布曲线与正态分布不符,所以在使用传统标准差法进行数据处理时,需要先通过计算剔除离群值。
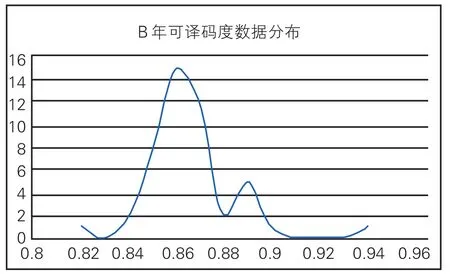
图2 B年可译码度数据分布
通过格拉布斯检验法计算表3中数据,可以计算出序号为47的数据为离群值,所以在进行数据处理时将其剔除,为了验证其是否剔除的合理,可以将47号数据带入Z比分数计算公式中,计算出其Z比分数值为4.96,远大于不满意结果值,所以将其剔除是合理的。此时从传统标准差法Z比分数可以看出,从序号2-45为满意结果,满意结果区间为0.84-0.89,满意结果区间相差0.05,与表1中结果对比接近。
周期性的开展检测能力验证,是维护与提升条码检测能力,掌握各检测机构条码检测能力、水平和环境的重要手段。
当使用中位值与标准化四分位距法计算Z比分数时,计算此组数据的中位值、高低四分位值,可以看出中位值和低四分位值相同,高四分位值和低四分位值相差较小,说明数据分布过于集中。假设此组数据用中位值与标准化四分位距法进行计算,表3中Z比分数只有序号4-38为满意结果,满意结果区间为0.85-0.87,满意结果区间相差0.02。然而根据条码检测设备的相关标准GB/T 26228.1-2010《信息技术 自动识别与数据采集技术条码检测仪一致性规范第1部分:一维条码》中对可译码度参数项的允许误差的要求,表3中数据使用中位值与标准化四分位距法计算出的满意结果范围对实际应用中的要求过于严苛,例如表3中可译码度值为0.88和0.89的数据同样出现了很多组,考虑在实际应用中的误差要求,当此组数据剔除离群值后的平均值作为标准参考值时,0.88和0.89应该被认同为满意结果。所以此次能力验证应根据实际应用要求情况,选择传统标准差法进行数据处理。
应用实例一中的数据接近于标准的正态分布,传统标准差法和中位值与标准化四分位距法均可作为数据处理的方法。而应用实例二中的分布非正态分布类型,其数据中有多个数据集中的地方,即分布图中有多个波峰,并且还存在个别离群值,需要根据实际应用场景选择合适的方法进行能力验证统计。
所以在计算Z比分数时,当数据分布接近标准正态分布,采用中位值与标准化四分位距法和传统标准差法的结果相近;而当数据分布较为复杂时,需要根据数据的应用需求来进行测试。

