车车通信环境下智能车辆安全自主换道
季亚平 张健 吴坤润 李青扬
1. 江苏省城市智能交通重点实验室(东南大学)江苏 南京210096 2. 现代城市交通技术江苏高校协同创新中心 江苏 南京210096 3. 江苏省物联网技术与应用协同创新中心江苏南京210096
在道路上,车辆的驾驶行为包括跟驰、换道和超车, 其中, 换道行为是在车辆跟驰状态之后, 是超车行为研究的基础和前提. 车辆的换道目的是实现主动避撞、更换至高速车道和安全超车[1]. 车辆的换道行为会对交通安全和效率产生重大的影响. 不安全的换道行为可能会引起周围车辆采取紧急制动的措施,从而导致交通事故和局部的交通拥堵[2]. 根据调查表明[3],由于换道产生的交通事故占所有交通事故的4%~10%,且导致的道路交通延误约占总延误的10%. 75%的换道事故发生的原因是驾驶员对周围车辆的信息感知不足[4]. 换道行为失败的主要原因是换道车辆与周围车辆之间缺乏信息交互. 随着信息技术的快速发展, 车联网已成为智能交通系统发展的重点和热点研究技术之一. 在车车通信的环境下, 智能车辆通过自身传感器获得车辆的运动状态信息(如GPS、加速度传感器等获得车辆的位置、速度、加速度等), 车辆之间通过无线通信技术进行全方位的动态实时信息交互[5],时刻掌握车辆彼此间的驾驶需求,实现智能车辆的自主性安全换道,进而形成安全和高效的道路交通环境.
换道车辆产生换道意图, 需要清楚地掌握当前周围车辆的运动状态信息和道路环境的信息, 以在合适的时间作出恰当的驾驶行为. 在车车通信的环境下,换道车辆与周围车辆实现实时信息交互,建立换道决策模型, 提高换道行为的安全性和高效性[6].针对智能车辆换道决策, 目前的研究建立的模型考虑了两车的安全距离、相对速度和避免碰撞时间作为制定换道决策规则[7]. 文献[8]提出了一种网联汽车分散式协同变道决策的框架,该框架由状态预测、候选决策生成和协同3 个模块组成. 为了保证智能车辆换道决策的安全高效性,文献[9]研究了一种基于驾驶员自身满意度的换道决策方法, 根据驾驶员的速度期望和安全距离期望建立了驾驶员的不满意度累积模型,保证换道过程的高效性和安全性. 车辆的换道决策符合博弈行为, 目前一些学者通过引入博弈论分别研究不完全信息和完全信息下车辆的换道行为特征. 文献[10]提出一种基于博弈论的车辆换道决策模型, 测试结果表明该博弈模型能够很好地模仿驾驶员的换道行为方式. 文献[11]针对智能网联汽车, 基于博弈论建立车辆协同机制的换道模型, 该模型在换道决策前后考虑换道车辆和周围车辆的驾驶风格和速度收益情况对换道决策的影响.
智能车辆基于换道决策模型, 在恰当时间下采取的换道驾驶行为需要保证换道过程的安全性和可靠性. 目前对智能车辆换道控制的研究, 传统的控制方法有比例积分微分(Proportional-Integral-Derivative,PID)控制、滑膜控制和模糊控制.由于智能车辆的动力学模型是非线性模型, 这些传统的方法在控制车辆的换道过程的准确性和安全性方面存在不足. 为了提高换道的安全性和鲁棒性,文献[12]基于安全距离模型和模糊控制理论建立了车辆纵向制动模型,实现对侧向换道路径的跟踪和控制.文献[13]提出一种基于神经网络与滑膜控制结合的神经滑膜轨迹跟踪控制器, 比传统滑膜控制器的鲁棒性好.为提高智能车辆自主转向的精确性和稳定性,文献[14]针对涉及自动驾驶和人工驾驶车辆的混合交通, 提出了一种基于模型预测控制的自动驾驶车辆避撞的控制策略. 文献[15] 基于场景模型预测控制的最新成果, 提出了一种用于高速公路车道变更辅助和自动驾驶的控制算法, 实验结果证明了场景模型预测控制算法的有效性和优化路径的快速性.
智能车辆安全换道过程主要包括换道决策和换道轨迹跟踪控制. 目前对智能车辆换道过程的换道决策和换道控制是单独分开研究的, 缺乏对智能车辆自主安全换道过程的整体研究.因此,主要内容是车车通信环境下智能车辆的自主安全换道过程. 实现智能车辆的整个安全换道过程的研究是极具意义的, 可以提高智能车辆在换道过程中的安全性和高效性,改善乘客体验感的舒适性,为智能网联汽车自动驾驶提供技术解决方案.
整个安全换道过程是在车车通信的环境下, 当换道车辆产生换道意图, 结合周围车辆的运动状态信息建立安全换道的博弈论决策模型, 分析获得的换道收益矩阵; 换道车辆接受到允许换道的指令后,进入换道轨迹跟踪控制器, 实现对规划的安全换道轨迹侧向位移函数的准确跟踪;借助仿真平台,联合仿真验证智能车辆整个安全换道过程. 在本文中,使用相当于SAE J3016(2018年6月修订版)标准中L3级别的自动驾驶车辆, 这种自动驾驶车辆仅需要驾驶员少量操作,而且整个换道过程的通信状态理想,不存在信息缺失、中断干扰现象,无延迟丢包.
1 智能车辆的换道过程
1.1 换道场景
车辆的换道行为可分为选择性换道和强制性换道[16], 侧重于车辆的自主性换道. 在实际的道路上,智能车辆的换道过程中需要考虑人、车、路、环境等影响因素, 鉴于智能车辆安全换道过程的研究主要是涉及同车道的前后两车之间的运动状态信息的交互,建立了一个简单局部的道路换道环境,换道场景的假设: 1)同道前车保持正常行驶不会妨碍后车换道; 2)换道车辆的目标车道有足够的空间且不会妨碍后车换道通行;3)整个换道过程中的通信理想,不存在信息缺失、中断干扰的现象.
简化的智能车辆的换道场景如图1 所示, Car 2表示同车道的后车,即是产生换道需求的车辆,Car 1表示同车道的前车;VX-1、VX-2分别表示前车和后车的纵向车速;V2表示后车的速度.
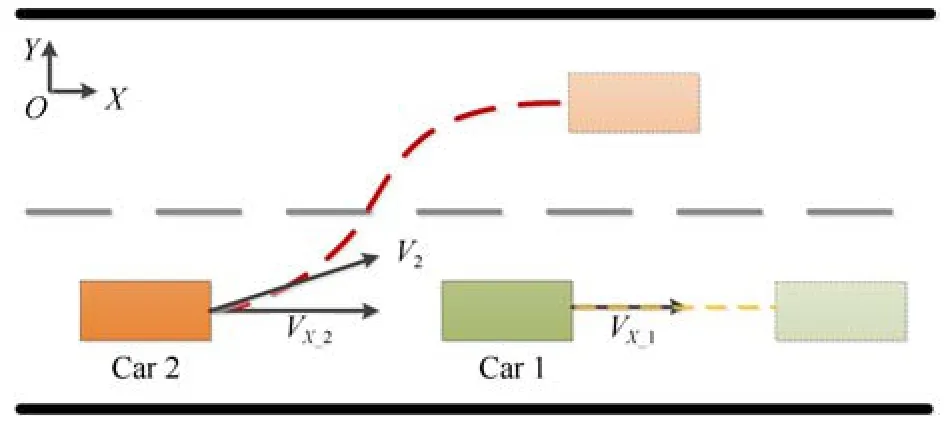
图1 智能车辆的自主性换道场景Fig.1 Autonomous lane-changing scenario of intelligent vehicle
1.2 智能车辆的换道过程
根据上面建立的简单局部换道场景, 智能车辆安全自主换道研究的系统流程图如图2 所示. 当换道车辆产生换道意图, 通过直接通信和周围车辆进行当前信息交流,建立安全换道的博弈决策模型,分析博弈换道收益矩阵, 判断当前是否允许后车采取换道措施;换道车辆接受到允许换道的指令后,进入模型预测换道轨迹跟踪控制器, 实现对规划的安全换道轨迹侧向位移的准确跟踪; 联合仿真验证智能车辆整个安全换道过程.
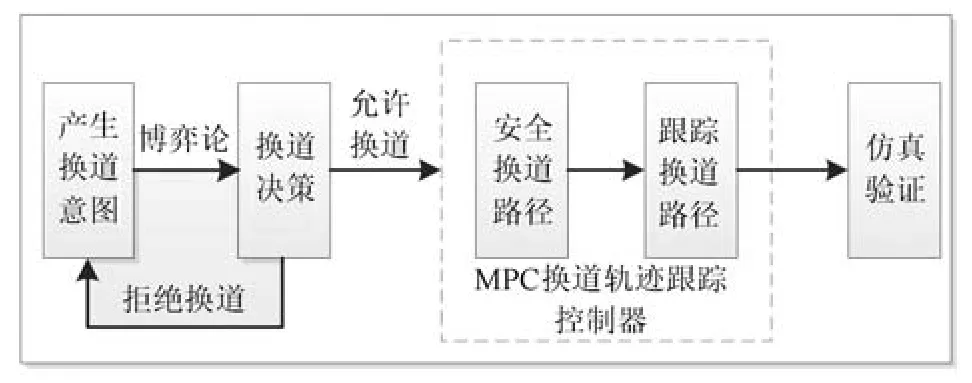
图2 智能车辆安全换道过程的系统流程图Fig.2 System fl w chart of intelligent vehicle safe lane-changing process
2 智能车辆的安全换道决策模型
2.1 完全信息下的博弈换道决策模型
智能车辆的换道过程中需要结合车辆自身的传感器, 车车通信技术获取得到全方位的实时路况和车况信息,换道车辆产生换道意图,将换道需求信息传至周围车辆, 与换道车辆处于同一车道的周围车辆接受到其换道需求后, 两车之间经过直接通信后交互当前的交通状态信息,采取双方共赢的策略.
完全信息下的博弈论换道决策, 能够反映两车在后方车辆产生换道需求的情况下, 两车各自选择的驾驶行为会形成博弈换道决策组合, 由此可以得到在不同的决策组合下,二者各自的博弈收益.提供给换道车辆采取的策略组合为{跟驰,换道},换道车辆的前方车辆可以采取的策略组合为{允许换道,拒绝换道}. 两车之间的博弈换道决策满足纯策略纳什均衡.
2.2 博弈换道决策函数的收益
博弈换道过程中, 换道车辆基于通信技术得到运动信息,采取恰当的驾驶行为决策,侧重于不同需求或期望的因素会导致决策后不同的驾驶行为[17].侧重于选择两车的相对速度和相对安全车距对博弈换道收益的影响. 博弈换道决策函数主要由两大部分组成, 分别是安全车距的收益函数和速度的收益函数,如式(1)所示.

其中,D表示安全车距的收益函数,S表示速度收益函数. α 和β 分别是安全车距和速度收益函数对应的权重系数,权重系数的选取范围如式(2)所示.

权重系数值的选取视安全车距和速度对博弈决策换道对博弈参与方的影响因素的要求来决定[18].例如, 依据政策, 消防、医护、公交等特种车辆具有更高的优先权,在博弈方具有相对优势.
2.2.1 前后两车的安全车距收益
在建立好的换道场景下, 前后车之间的安全车距是博弈换道决策过程中两车权衡利弊的重点. 为保障后车换道过程中与前车保持一定的安全车距避免发生碰撞, 这里主要考虑的是两车之间的纵向安全车距, 安全车距的收益函数需要基于最小纵向安全车距模型, 为当前两车的相对车距和最小安全车距的差值同最小安全纵向车距的比值.
安全车距收益函数如式(3),最小安全纵向车距如式(4)所示.

其中,H为前后两车的相对车距,DS为两车的最小纵向安全车距.

其中,VX-1、VX-2分别为前车和后车的纵向速度,aX-1、aX-2分别为前后车的纵向加速度,t表示后车制动滞后的时间.
2.2.2 前后两车的速度收益
两车初始状态为跟驰模型, 处于同车道的前后车的换道决策, 需要考虑采取不同的策略下各自的速度变化带来的收益情况.
两车的策略组合分为4 种情况. 第1, 换道车辆的前方车辆采取{拒绝}策略, 即保持原来的速度状态信息,速度收益为0; 换道车辆在接受到前方拒绝换道请求后,选择{跟驰}策略,速度收益为两车之间的相对速度. 第2, 换道车辆的前方车辆采取{拒绝}策略,速度收益为0;换道车辆在接受到前方拒绝换道请求后,坚持选择{换道}策略,速度收益为换道车辆采取该策略需要保持安全距离下的期望速度与当前速度的差值.第3,换道车辆的前方车辆采取{允许}策略,速度收益为需要通过加速或保持速度来达到安全车距下的期望速度与当前速度的差值; 换道车辆在接受到前方拒绝换道请求后, 选择{跟驰}策略, 速度收益为前方车辆的期望速度与换道车辆当前速度的差值. 第4, 换道车辆的前方车辆采取{允许}策略,速度收益为需要通过加速或保持速度来达到安全车距下的期望速度与当前速度的差值; 换道车辆在接受到前方拒绝换道请求后, 选择{换道}策略, 速度收益为换道过程中与前车保持安全车距的期望速度与当前速度的差值. 具体的速度收益矩阵如表1 所示.

表1 速度收益矩阵Table 1 Gain matrix based on speed
其中, 括号内的第1 项数据和第2 项数据分别为换道车辆的前方车辆和换道车辆的速度收益值. {拒绝}和{允许}是前车采取的策略组合, {跟驰}和{换道}是换道车辆采取的策略组合;E1、E2 分别为两车在当前策略下期望达到的车速,V1、V2 分别为两车的车速.
3 智能车辆的换道控制
3.1 车辆的动力学建模
在对智能车辆进行换道控制的过程中, 由于换道行为的实际情况复杂, 建立车辆的动力学模型可以满足多个状态变量, 控制变量和道路情况的约束条件, 因此, 能够满足换道轨迹跟踪控制器的需求.车辆动力学模型是一种非线性模型,如图3 所示. 对图3 中动力学模型的主要变量解释如下:
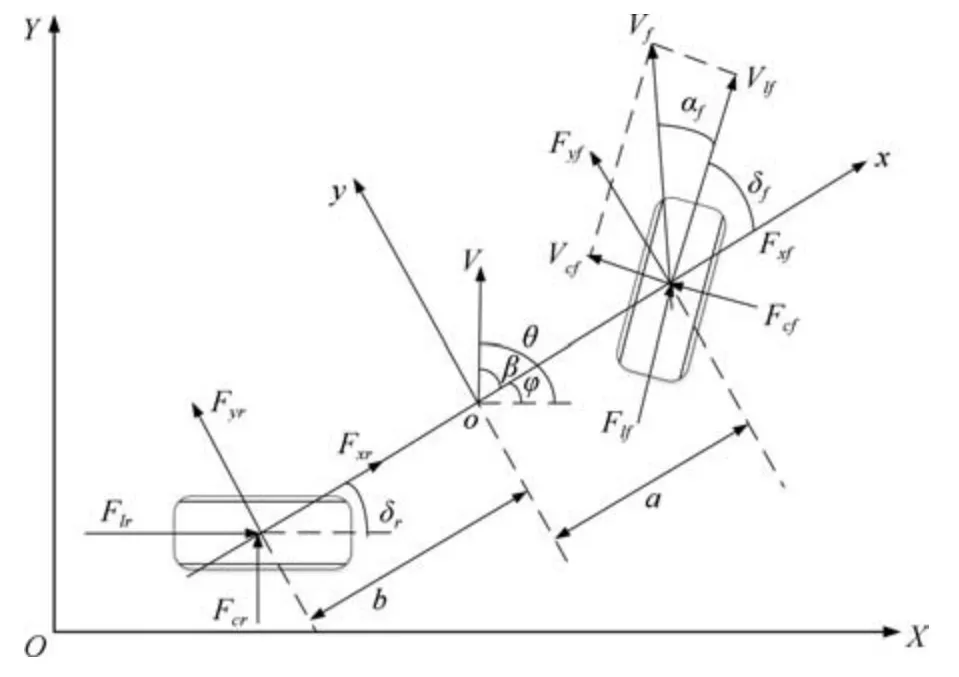
图3 车辆动力学模型Fig.3 Vehicle dynamical model
图中,Flf、Flr为车辆前轮、后轮纵向力;Fcf、Fcr为车辆前轮、后轮横向力;Fx f、Fxr为车辆前轮、后轮x方向的力;Fyf、Fyr为车辆前轮、后轮y方向的力;α 为侧偏角;β 为质心侧偏角;φ 为横摆角;θ 为航向角; δ 为轮胎的转向角; 上述变量的下标f表示前轮,r表示后轮.
3.2 MPC 轨迹跟踪控制器的设计
模型预测控制(Model Predictive Control, MPC)属于负反馈控制,相较于传统的PID 控制,不仅利用当前和过去的偏差值, 还建立预测模型来预测未来时刻的偏差值. 文献[19] 指出模型预测控制相较于其他的控制方法, 优势在于能够实现一个优先的预测时域来预测未来的一段时间,滚动优化,反馈校正.将模型预测控制理论运用到对车辆换道轨迹的跟踪,能够更加准确地捕捉到换道过程中的运动状态信息,实现良好的横向跟踪控制.
因此, 在后方车辆接受到允许换道命令的时候,选用基于模型预测控制理论来设计换道车辆的轨迹跟踪控制器, 实现换道车辆在期望的换道路径下的跟踪控制.MPC 轨迹跟踪控制器的设计包含3 个方面: 线性误差模型、目标函数和约束条件.
3.2.1 线性误差模型
在此换道轨迹跟踪控制器, 系统的输入状态变量分别为质心侧偏角、横摆角速度、侧向位移、航向角、纵向位移和速度.控制器通过控制车辆的方向盘转向角来实现与期望的换道路径的跟踪. 基于3.1 部分搭建好的动力学模型, 车辆的动力学模型表达式如式(5)设计系统的状态量和控制变量的表达式,分别如式(6)、式(7)所示.

则可以得到系统的线性时变方程如式(8)所示.再将系统的线性时变方程进行离散得到误差模型如式(8)、式(9)所示. 式(8)、式(9)中的III表示全为1的矩阵,TTT为时间矩阵.
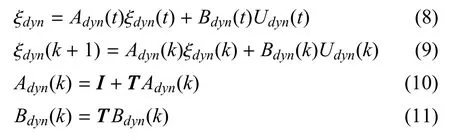
3.2.2 目标函数
换道轨迹跟踪控制器的目的函数主要包括两部分内容, 分别为实际输出的侧向位移和期望的侧向位移换道轨迹之间的偏差, 以及作为控制变量的方向盘转向角在每一个采样周期内的增量. 参照文献[20],采用软约束使运行的速度会更快,因此,目标函数的设计如式(12).

其中,Np为预测时域,Nc为控制时域,ρε2为添加的松弛因子,η 为轨迹离散点,下标ref表示参考轨迹,下标dyn表示动力学模型.
3.2.3 约束条件
换道轨迹跟踪控制器是通过控制车辆的方向盘转向角来控制车辆的侧向位移变化. 为使控制器的预测效果更好, 选择对方向盘的转向角的变化量在每一个控制时域内设置约束条件(i= 0,1,··· ,Nc−1),具体约束条件如式(13).

其中, Δumin(k+i)表示控制变量增量的最小值,Δumax(k+i)表示控制变量增量的最大值.
4 仿真结果分析
4.1 Matlab/Simulink 系统建模
借助Matlab/Simulink 和CarSim 两个仿真平台搭建简单的两车道两车的换道场景, 实现智能车辆整个换道过程, 包括换道决策和换道轨迹跟踪控制.具体搭建的Simulink 系统模型如图4 所示. 图4 主要模块是lane-changing decision 和MPC controller,分别为博弈换道决策模型和模型预测控制轨迹跟踪器.
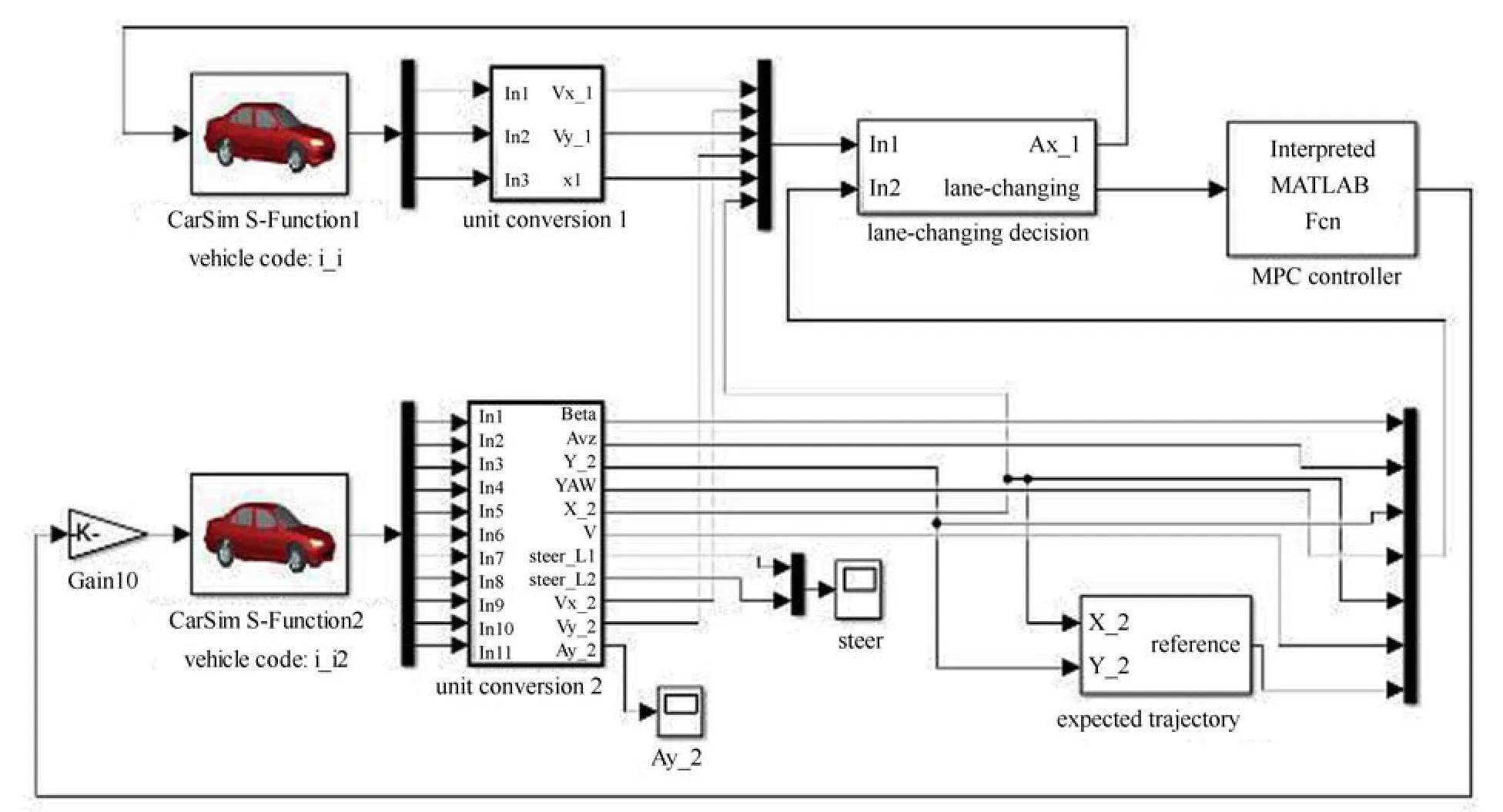
图4 Matlab/Simulink 仿真平台建模Fig.4 Matlab/Simulink simulation modeling
4.2 仿真结果验证
为了验证博弈决策模型和模型预测换道控制模型在智能车辆自主安全换道的安全性和精确性, 选用了模糊控制理论对智能车辆进行换道控制. 车辆动力学模型是非线性模型, 模糊控制是模拟驾驶员的驾驶思想, 借助自身较好的鲁棒性解决非线性的问题[21]. 对比实验中设计的模糊换道控制器基于模糊控制理论, 输入变量为两车的相对速度和相对距离,控制换道车辆的方向盘转向角,以实现对车辆的换道控制.
选取两车在换道过程中的相对距离和换道车辆的侧向速度值,作为定量分析换道安全性的指标.
4.2.1 仿真结果
在仿真实验中, 设置初始状态, 换道车辆的前方车辆的车速为V1=60.00 km/h, 换道车辆的车速为V2=40.00 km/h,在设定的换道场景,两车位于同一车道内,初始的纵向相对车距为30 m.
进入建立好的博弈换道决策模型. 考虑目的是实现换道车辆的整个安全换道, 在换道决策过程中倾向于安全车距的收益. 因此, 在实验中, 将2.2 提到的博弈换道收益函数式(1)中的权重系数设置为α = 0.7 和β = 0.3;仿真运行的结果得到如表2 的收益矩阵,满足纯策略纳什均衡得到的决策组合是{允许,换道},也就是{前车允许换道,后车换道}.

表2 博弈决策收益矩阵Table 2 Gain matrix based on game theory
经过博弈决策换道模型得到允许后车换道的命令之后,后车进入换道轨迹跟踪控制器. 联合仿真得到MPC 换道轨迹跟踪器的效果如图5、图6 所示.在图5 中,换道车辆的实际输出侧向位移同期望的侧向位移几乎重合,可以验证MPC 换道轨迹跟踪控制器的跟踪效果良好.由图6 换道车辆的实际侧向位移和期望换道路径的侧向位移偏差控制在0.1 m,表明MPC 控制器能够保证智能车辆自主换道的精确性,进一步实现安全换道. 在换道过程中,换道车辆的方向盘转向角的输入情况如图7 所示.

图5 MPC 控制器下换道车辆的期望和实际输出的侧向位移对比曲线Fig.5 Comparison curve of the expected and actual output lateral displacement of the lane-changing vehicle under the MPC controller

图6 MPC 控制器下换道车辆的期望和实际输出的侧向位移的偏差值曲线Fig.6 The deviation curve of the expected and actual lateral displacement of the lane-changing vehicle under the MPC controller

图7 MPC 控制器下换道车辆的转向角情况Fig.7 Change of steering angle of lane-changing vehicle under MPC controller
4.2.2 对比研究仿真结果
为验证采用模型预测控制器跟踪车辆的换道轨迹的准确性和安全性, 在目前已研究的换道控制方法中,选用模糊控制原理设计了模糊换道控制器,仿真实验中换道场景和工况设置与本文方法一致.
智能车辆的自主换道需要保障安全性, 换道车辆的侧向速度和侧向加速度在换道过程中都需要满足安全避撞条件. 此外, 从空间角度, 选用换道过程中两车的相对位移作为分析换道安全性的指标.
MPC 控制器下, 车辆的侧向速度和侧向加速度分别如图8 和图9 所示;两车在换道过程中的相对位移如图10 所示. 对比研究设计的模糊控制器下, 换道车辆的侧向速度和侧向加速度在换道过程中变化值分别如图11 和图12 所示;两车在换道过程中的相对位移如图13 所示.

图8 MPC 控制器下换道车辆的侧向速度变化曲线Fig.8 The lateral speed curve of the lane-changing vehicle under the MPC controller
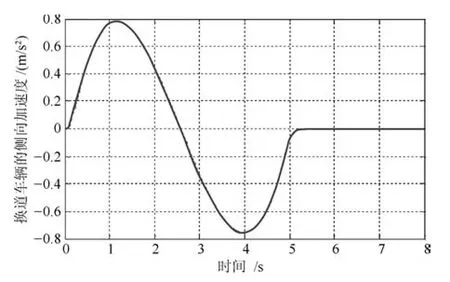
图9 MPC 控制器下换道车辆的侧向加速度变化曲线Fig.9 The lateral acceleration curve of the lane-changing vehicle under MPC controller
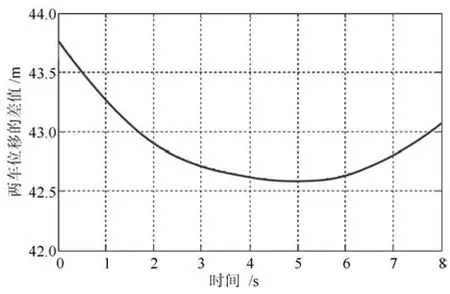
图10 MPC 控制器下两车的相对位移变化曲线Fig.10 The relative displacement curve of the two vehicles under the MPC controller

图11 模糊控制器下换道车辆的侧向速度变化曲线Fig.11 The lateral speed change curve of lane-changing vehicles under fuzzy controller
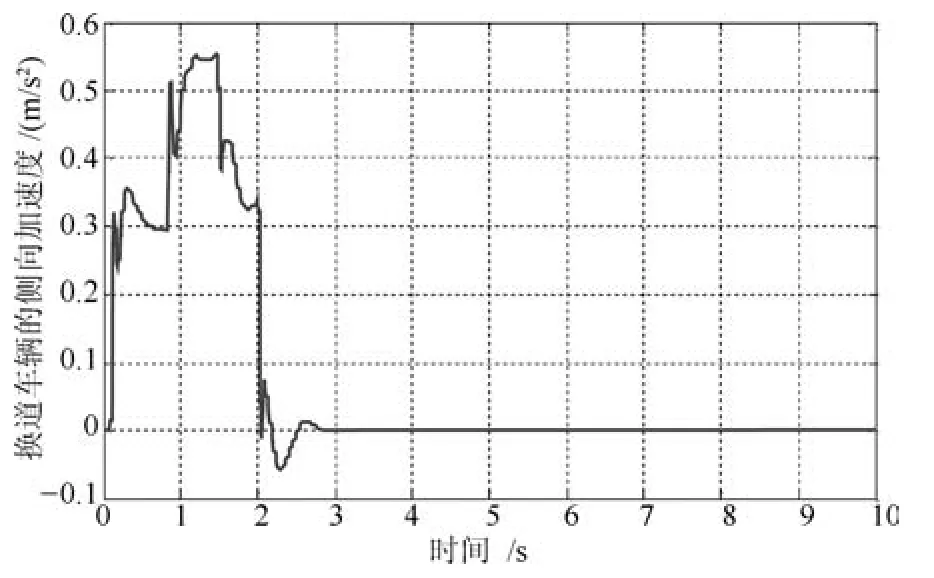
图12 MPC 控制器下换道车辆的侧向加速度变化曲线Fig.12 The lateral acceleration curve of the lane-changing vehicle under the MPC controller
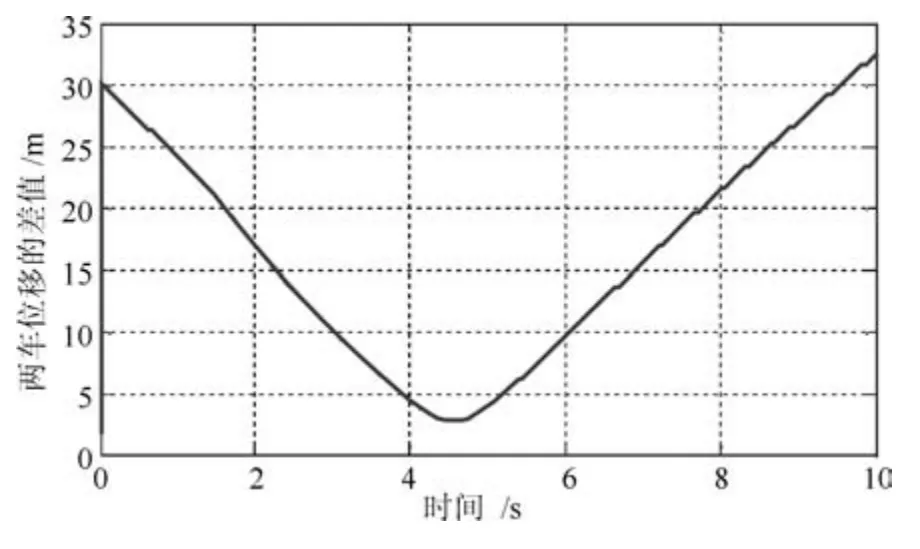
图13 模糊控制器下两车的相对位移变化曲线Fig.13 The relative displacement curve of the two vehicles under the MPC controller
由图8 和图11 对比,模糊控制器下换道车辆的侧向速度的最大值小于0.09 m/s,满足车辆自主安全换道避撞条件. MPC 控制器下, 换道车辆的侧向速度的最大值小于0.04 m/s, 相较于模糊控制器, MPC轨迹跟踪器下换道车辆的侧向速度最大值下降了55.6%.
由图9 和图12 对比,模糊控制器下换道车辆的侧向加速度的最大值小于0.8 m/s2, MPC 控制器下,换道车辆的侧向加速度的最大值小于0.6 m/s2. 二者控制下的侧向加速度都满足车辆自主安全换道避撞条件.
由图10 和图13 对比,模糊控制器下,两车在换道过程中相对距离的最小值大于3.0 m,MPC 控制器下, 两车相对距离的最小值大于42.5 m. 显然, 在同一工况下,相较于模糊控制器,MPC 轨迹跟踪器下两车的相对距离更大. 这表明换道过程中两车的距离满足安全避撞.
因此, 仿真结果表明基于模型预测控制设计的换道轨迹跟踪控制器, 能够实现智能车辆更安全的自主换道.
5 结论
基于车车通信技术, 智能车辆在简单的两车道换道场景,实现了整个安全换道过程,建立了换道决策模型, 通过博弈决策换道模型获得当前时刻最佳的策略,当后车获得允许换道的策略,再通过基于模型预测控制原理设计的控制器, 对期望的换道路径进行安全且准确的横向追踪. 最后,通过与已研究的方法进行仿真对比,验证博弈换道决策模型和MPC轨迹跟踪控制模型能够实现智能车辆自主安全换道.
不足之处在于: 1)整个换道流程的场景可以扩展至多车道; 2)考虑换道车辆相邻车道的周围车辆的影响因素,博弈论换道决策模型也有待深入研究;3)进一步考虑换道过程时间演化的问题;4)接下来考虑使用SUMO 或PreScan 等其他仿真软件, 进一步研究通信问题对智能车辆换道控制带来的影响.上述问题也作为今后研究展望.

