基于Fisher信息矩阵的多目标最优传感器配置

王琦少 王青云 段志生

1．北京航空航天大学航空科学与工程学院北京100191 2. 北京大学工学院北京100871

态势感知[1−3]是复杂战场情况下实现指挥与控制的基础之一,目标感知问题[4−5]是战场态势感知问题的一个重要分支,在潜水艇、船舶以及防御监视系统对目标的定位问题中扮演了重要的角色. 对敌我双方实现精确的目标感知, 是对战场态势感知的基础, 传感器与感知目标之间的相对位置对感知精度有着较大影响, 良好的传感器部署可以实现对敌我双方态势更精准的把握. 为了解决传感器的最优部署问题,学者们已经提出了许多有效的算法[6−7]. 在此基础上,文献[8−9]指出对于多传感器非线性观测模型, 传感器与目标的相对几何构型对目标定位算法的表现有着显著的影响.因此,在何种条件下目标定位算法可以实现更好的性能是一个有意义的研究课题. 本文主要研究了如何基于FIM 和克拉美- 罗下界(Cramer-Rao Lower Bound, CRLB)来设计最优传感器- 目标相对几何构型的问题, 此问题也称为传感器部署问题. CRLB 和FIM 通常用来评估状态估计算法的性能[9]. FIM 与传感器部署位置,即传感器-目标的相对几何构型有关, 可以看作一个以传感器-目标几何构型为自变量的矩阵函数. CRLB 是FIM 的逆矩阵, 用于估计协方差矩阵可以到达的下界,即无论状态估计算法如何设计,估计误差协方差矩阵不可能小于CRLB. 值得一提的是, CRLB 受传感器- 目标的几何构型影响, 与滤波算法的选取无关.许多研究表明,CRLB 最小化的几何构型更有可能达到精确的目标定位效果.

目前衡量最优传感器-目标相对几何构型的性能指标主要有两种: A 类最优标准与D 类最优标准.其中, A 类最优标准要求最优的几何构型能够最小化CRLB 的迹, 而D 类最优标准则要求最优的几何构型能够最小化CRLB 的行列式或最大化FIM 的行列式.

基于A 类最优标准与D 类最优标准的单目标定位问题已经有许多优秀的研究成果[10−23]. 其中,文献[12−13] 研究了异构多传感器在二维空间中的最优部署问题,分别给出了基于A 类最优标准以及D 类最优标准的解析形式的最优构型. 文献[13]对二维情形不同种类传感器的最优构型做出了综合性的讨论.在此基础上, 文献[14−15]分别讨论了二维情形下含区域约束的多传感器最优构型, 以及二维情形下以最优构型跟踪移动目标的问题.基于D 类和A类最优标准,文献[16,18]分别给出了二维情形下携带不同类型传感器的无人机最优路径规划策略. 文献[17]给出了一种确定异构多测角传感器在三维空间中所有最优几何构型的方法. 文献[21]进一步建立了三维空间中基于A 类最优标准的多接收信号强度传感器的最优几何构型条件.

在关于多传感器最优观测构型的文献中, 讨论的重点主要集中在比较简易的二维情形下多传感器最优构型问题. 对于更贴近实际的三维情形下多传感器的最优构型问题, 由于三维CRLB 的行列式难以计算, 所以研究得较少. 此外, 现有研究内容大多基于单目标的多传感器最优构型问题, 对于多目标多传感器最优构型问题的研究尚不充分.

文献[24] 指出, 在设计多传感器最优观测几何构型和轨迹优化时, D 类最优标准的连续性优于A类最优标准.同时,信号强度传感器在三维空间目标定位问题中已经得到了广泛的应用. 因此,本文研究了三维空间中, 基于D 类最优标准的多目标多信号强度传感器最优观测几何构型问题. 通过正定矩阵不等式放缩方法, 给出了针对单个目标的多传感器最优观测构型, 并在此基础上对多目标问题的优化指标进行了合理的修改, 实现了多传感器在多目标情形下的最优观测构型求解.

1 预备知识

1.1 基本概念

为了表征传感器几何配置对观测性能的影响,引入基于CRLB 的协方差矩阵表达式如下:

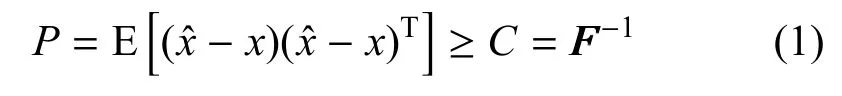
其中,x∈Rn为待估计向量,若考虑三维空间情形下的目标位置信息,则有n= 3；是x的估计值；P表示估计误差的协方差矩阵；C为CRLB,即正定二次型意义下协方差矩阵的下界；FFF为FIM,其表达式为

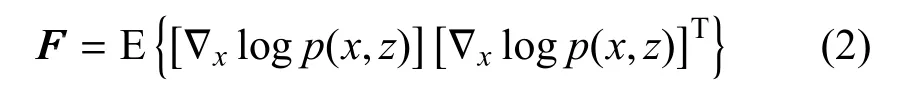
其中,p(x,z)为似然函数.

1.2 重要引理

在给出本文主要结果前, 先介绍几个重要的引理. 这些引理对于文章主要结果的导出起到了关键的作用.

引理1.对于一个大于等于三的整数α = 0,下式成立

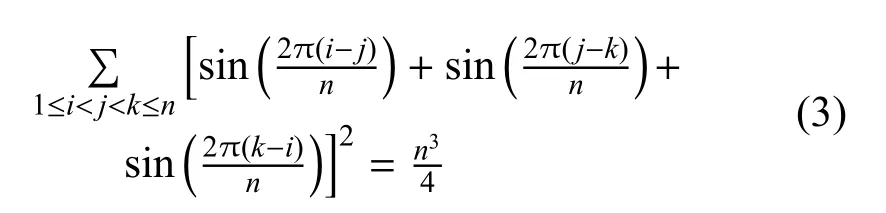
引理2.对于一个n×n的正定阵A,有

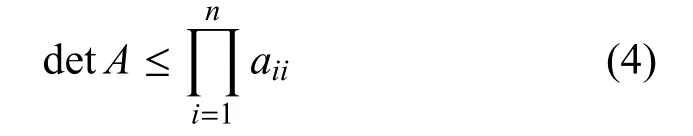
其中,aii是A的第i个对角元素,当且仅当A的非对角元全为0 时,等式成立.

证明.正定矩阵A可以写为

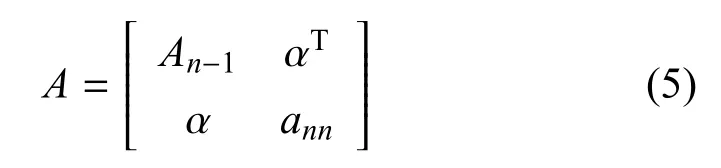
经过初等行变换,以下不等式成立

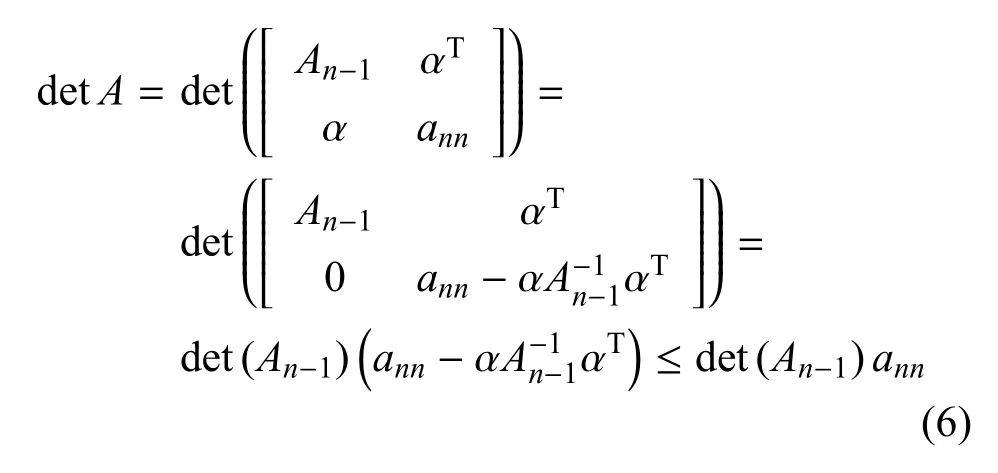
等式成立当且仅当α=0,由数学归纳法,引理得证.

2 传感器最优配置方法

2.1 传感器模型描述

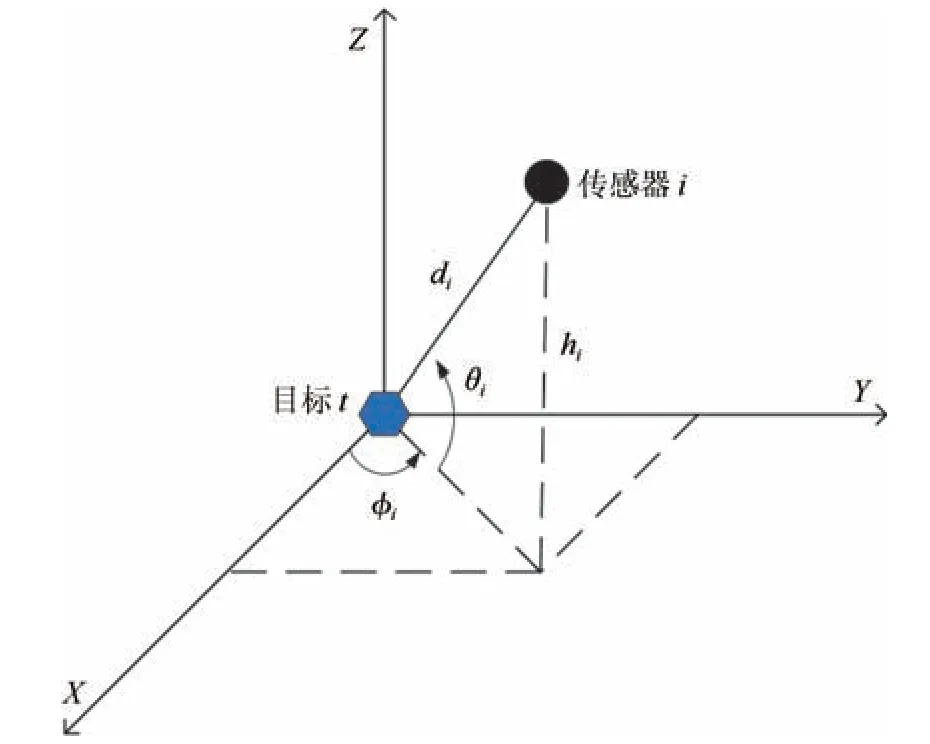
图1 传感器与目标相对空间位置示意Fig.1 The relative geometry between target and sensor

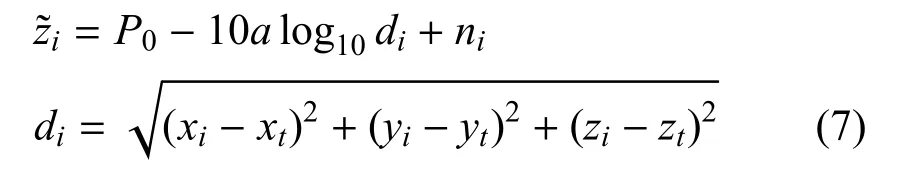
其中,P0是目标初始的信号强度；a是与环境相关的路径损失参数；di是传感器与目标之间的距离以及是加性的高斯白噪声,服从正态分布

2.2 多信号接收强度传感器下Fisher 信息矩阵

假设各传感器的噪声互不相关, 并且具有相同的方差,即σ1=σ2=···=σN=σ. FIM 的计算公式如下:

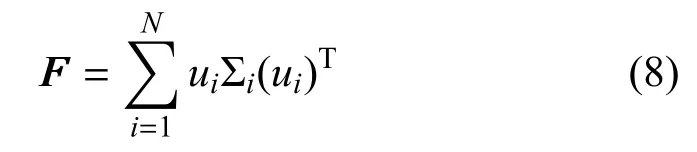
其中,

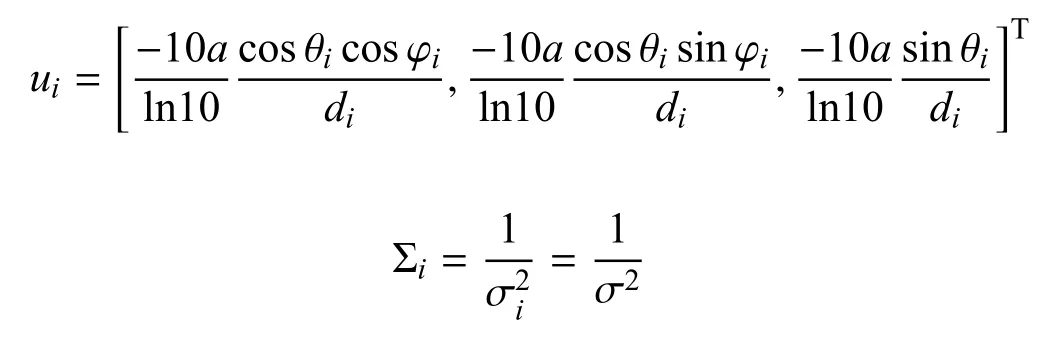
由上式可知,Fisher 信息矩阵可以表示为N个秩为1 的矩阵之和,将其表示为如下紧凑的形式

后面将讨论与FIM 相关的优化指标,并给出最优构型的表达形式.

2.3 D-优性能指标下最优构型的表达形式

基于FIM 的优化指标包括D-优,A-优,E-优等,其中, D- 优代表CRLB 的行列式, A- 优代表CRLB的迹,E-优代表CRLB 的最小特征值.这3 种优化指标的物理意义分别为误差椭球的体积、半轴长的和以及最短半轴长.

文献[24] 通过数值实例验证了D- 优指标相对于A-优和E-优而言具有更好的连续性,因而具有更好优化效果.本文采用D-优指标来求解最优观测构型. 由于Fisher 信息矩阵与CRLB 是互逆的关系,可以通过最大化Fisher 信息矩阵的行列式值来求解最优观测构型. 经过一定的计算,将Fisher 信息矩阵的行列式表达为下述的形式

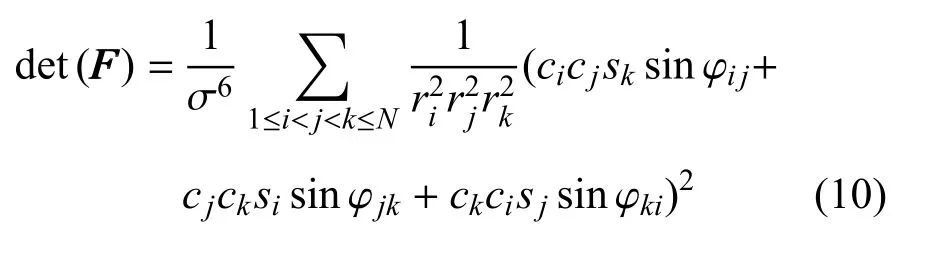
其中,ci=cos θiφi j=φi−φj.

本文考虑文献[23]提出的海平面单目标多传感器最优构型配置问题, 即在海平面上配置一系列传感器来观测水下目标, 已知目标与海平面的距离h.基于上述的分析,容易得到下述关系式

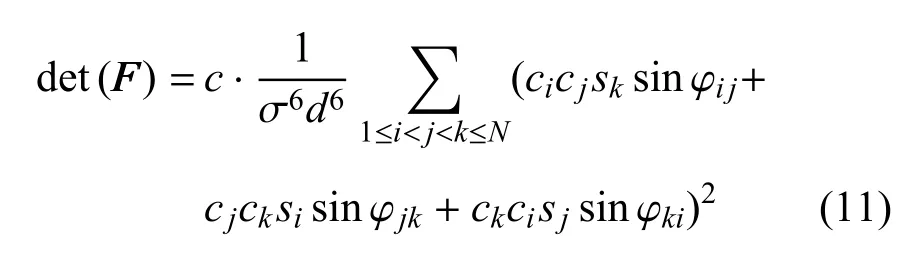
考虑几何对称的情形,即s1=s2= ··· =sN, 可以得到表达式

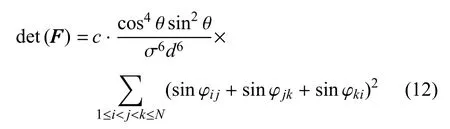
由引理3,可以得知FIM 的行列式值不会超过其对角线元素的乘积,即

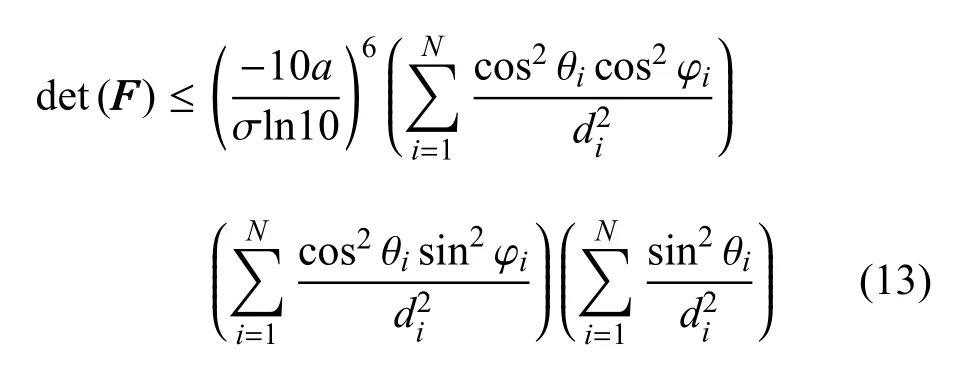
注意到上式中间两项具有如下的关系

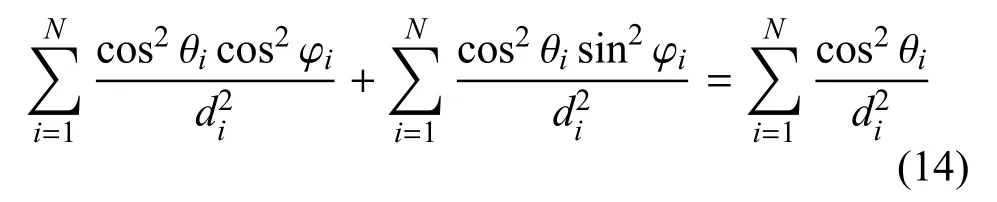
因此,可以将FIM 的上界进一步放缩为

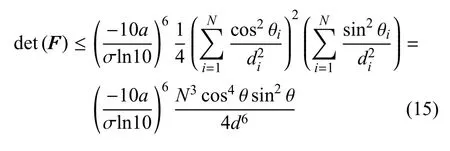
不难发现,当偏航角满足关系

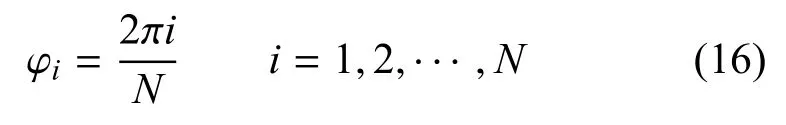
时,FIM 中的非对角元素均为0,即

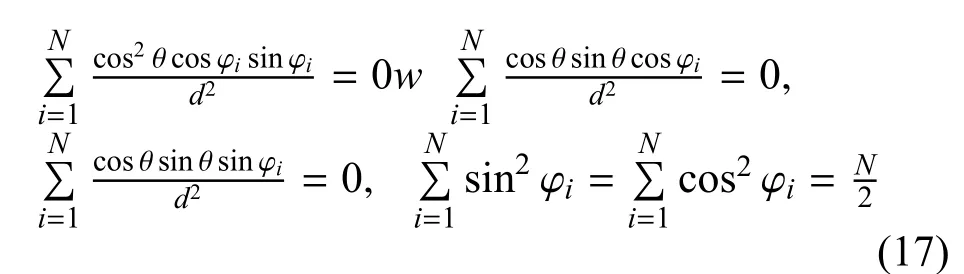
因此, 对于任意确定的θ, 取φi=即可使FIM 的行列式值达到上界,后续只需优化这一上界即可.将代入FIM 的上界表达式中,可以得到

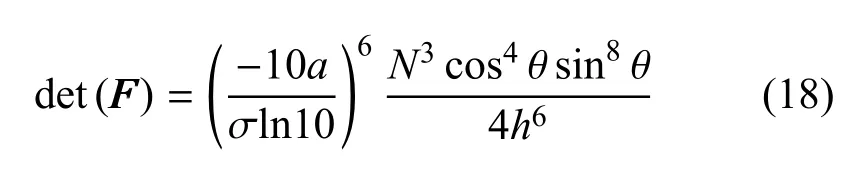
令x=sin2θ,容易发现上述表达式的最大值在x=即θ = arcsin处取到. 综上所述,最优传感器观测构型对应的俯仰角和偏航角为

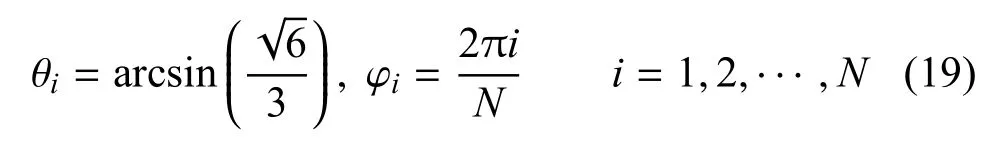
相应的最优Fisher 信息矩阵行列式值为

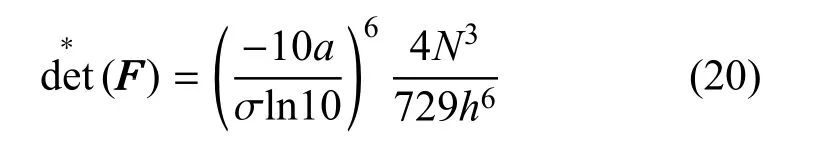
这一结果与引理1 中的内容相吻合.

由式(20)可以看出,对于最优观测构型而言,其所对应的FIM 行列式的值仅与传感器个数以及传感器与目标的距离有关. 这一结论为后续设计多目标最优观测构型提供了理论基础. 与文献[17, 21]仅讨论A 类标准的最优构型相比,本文利用正定矩阵的放缩方法给出了D 类标准下的最优观测构型. 单个目标传感器个数分别为4 和6 对应的最优观测构型示意如图2 所示.

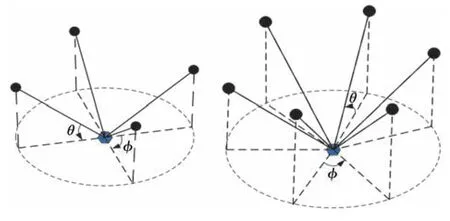
图2 单个目标最优几何构型示意Fig.2 Illustrative example for single target optimal observation geometry

2.4 多目标最优构型的表达形式

基于上一节的分析, 可以得到对于一个目标而言, 在指定了传感器的个数以及目标传感器之间的距离后, 其最优观测构型和对应的FIM 的行列式值都可以解析表出. 本节将针对多个目标的协同观测问题, 设计相应的优化指标来实现多传感器对多目标的最优观测配置.记

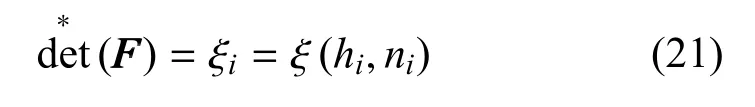
其中,hi是指定的高度,ni是指定的传感器个数,ξi表示第i个目标对应的最优Fisher 矩阵行列式值,满足

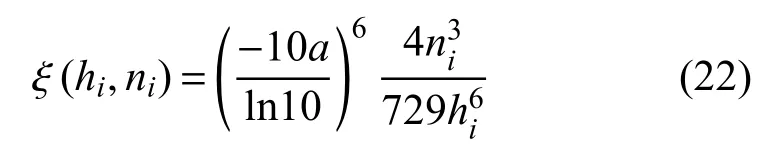
借鉴文献[19] 的处理方式, 将多目标传感器个数分配问题写为如下的优化问题

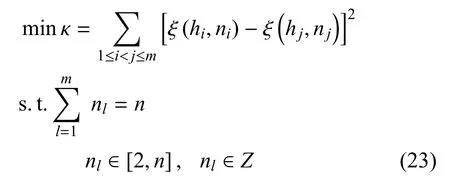
该优化问题的目标是使每一个目标对应的FIM行列式值尽可能地接近.在实际应用中,FIM 的行列式值是相对于深度h和数量N的高阶量, 这会导致优化问题的求解偏向于边界取值.因此,对优化指标进行修改,得到如下优化问题,其物理意义使每一个目标观测误差椭球的半长轴的几何均值尽可能接近.

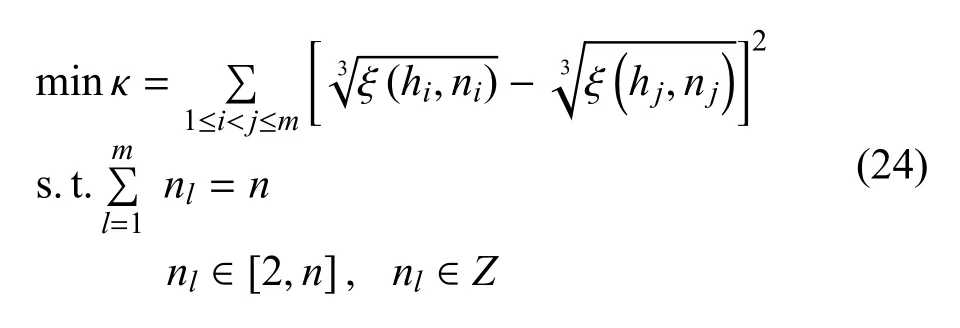
通过求解上述优化问题, 可以获得多目标传感器的最优配置构型.

从优化指标中可以看出, 如果传感器距离目标越远, 那么优化问题的解就会倾向于给该目标分配更多的传感器以实现观测效果的平衡. 与文献[19]相比, 本文将多传感器对多目标的最优观测构型求取方法推广到了三维情形, 并对优化指标进行修改从而优化了解的性质. 因此,本文所讨论的内容更加贴近实际应用.

3 数值验证

本节将通过一组数值实例来阐述优化问题的求解过程以及最优观测构型相较于普通观测构型的优势.

考虑的场景是我方在海平面上方有14 个携带信号强度传感器的侦察无人机,已知在水下有3 个待感知的敌方目标,其坐标、深度分别如表1 所示. 每一个侦察无人机可以观测一个目标, 为了实现对敌方3 个目标的最优感知, 需要求解式(24)所示的优化问题以获得最优的观测构型配置. 其基本步骤是得到每一个目标的传感器个数配置后, 针对每个目标配置最优的观测构型,以实现最优观测效果.

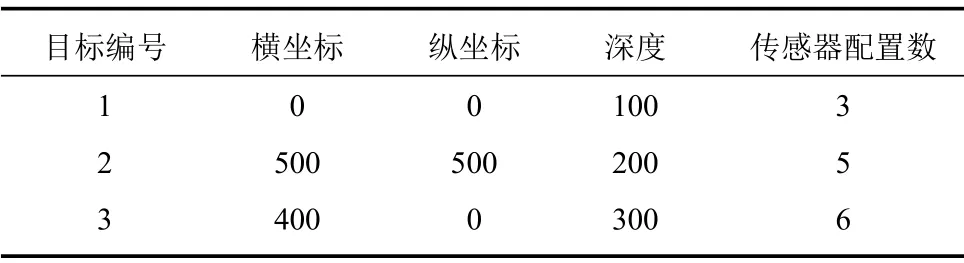
表1 目标参数以及最优传感器配置数Table 1 Parameters of targets and optimal allocation of sensors

图3 和图4 展示了最优传感器配置结果,黑色圆点代表我方侦察无人机, 蓝色三角形代表敌方水下目标, 两图分别展示了我方侦察无人机为实现对敌方目标最优感知所形成的三维几何部署和几何部署俯视图.

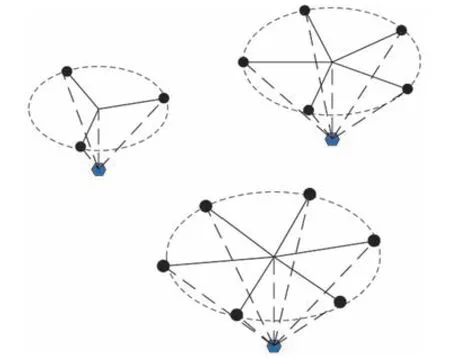
图3 最优传感器构型配置空间情形Fig.3 3D case optimal observation geometry for multiple sensors

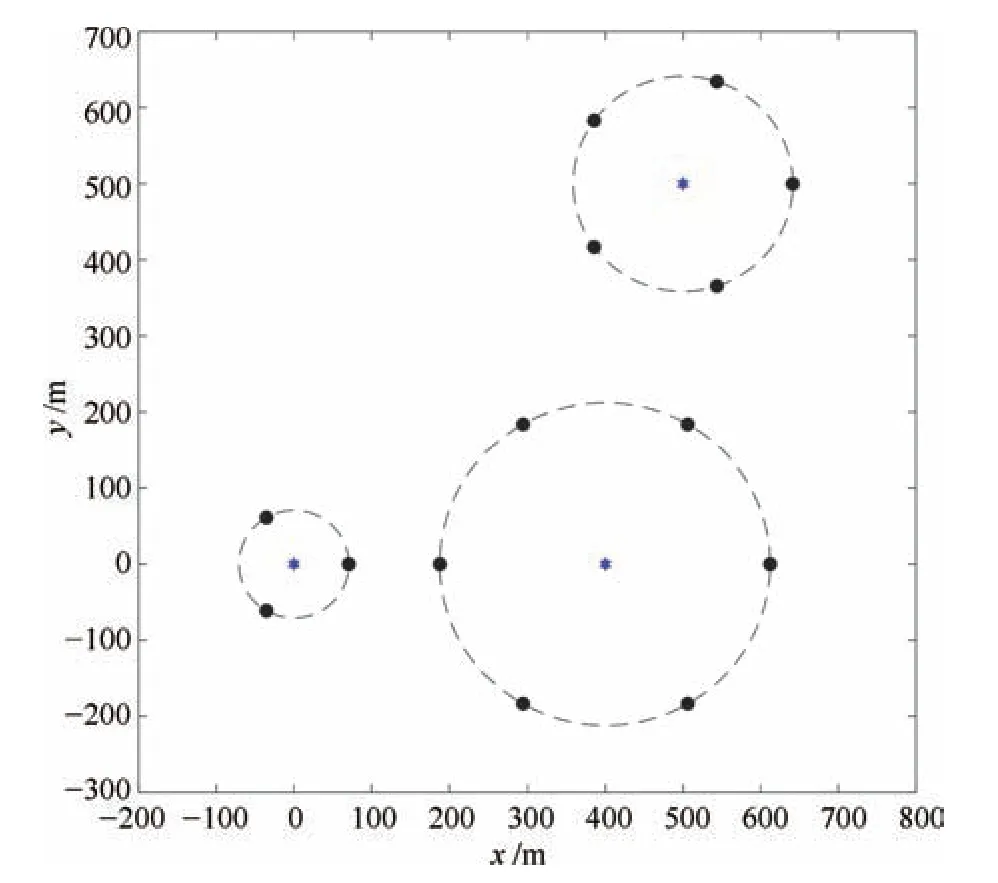
图4 最优传感器构型配置俯视图Fig.4 Top view of optimal observation geometry

图5 给出了最优构型与普通构型的观测性能对比结果. 仿真中, 不同的θ 代表不同的观测构型, 并采用扩展Kalman 滤波的算法进行观测, 记录方差项P的迭代值,记录不同观测构型下方差项P的迹trace(P)随时间的变化趋势. 可以看出, 最优构型下P的收敛速度和精度明显优于非最优构型下的情形,因此,最优观测构型的有效性得到了验证.

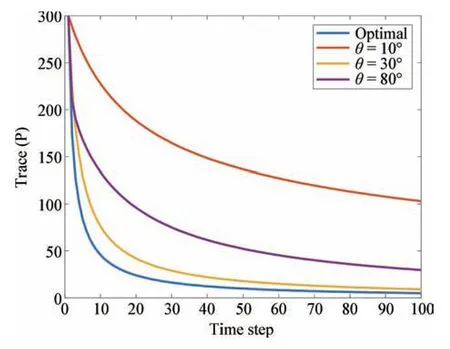
图5 不同观测构型下的trace(P)对比Fig.5 Comparison of trace(P)for different observation geometry

4 结论

本文考虑了战场态势感知中, 采用多传感器实现多目标感知的最优几何部署.通过优化FIM 的行列式值,得到了针对单个目标的最优观测构型. 对于多目标的情形, 将优化问题分解为传感器个数分配问题和单目标最优观测构型问题, 最终达到更好地观测效果.