基于双树复小波包及SVM的齿轮故障诊断
钱昭勇 曹裕华 张雷 秦海峰
1. 航天工程大学研究生院北京101416 2. 国防大学联合勤务学院北京100858 3. 西安卫星测控中心陕西西安710043
我军卫星的在役考核与美军对卫星后续作战试验鉴定类似, 主要立足部队实际, 结合平时成建制、成体系的训练、演练,全时空、全领域、全要素地跟踪掌握卫星使用、保障和维修情况,既考核卫星适用性和服役期的经济性, 又检测部分在性能试验和作战试验阶段难以考核的指标. 在役考核核心目的在于确保装备“好用”, 所以卫星系统在役考核的核心目的也应是解决“好用”的问题,而“好用”的基本前提就是确保卫星系统的性能可靠. 齿轮是卫星传动与控制系统的重要组成部件之一, 在机械动力及运动的传递中起着极其重要的作用. 由于在轨卫星本就处于复杂的电磁环境中,齿轮高速、重载地持续工作,导致齿轮故障问题概率大大增加,这些故障轻则影响系统分系统或整星性能, 重则使卫星驱动结构瘫痪, 不能转动太阳能电池板, 卫星将失去供电, 甚至成为太空垃圾[1−2]. 因此,在卫星的在役考核中,采取科学有效的算法,建立可信准确的数据模型,对齿轮故障进行及时诊断和准确分类是检验和确保在役卫星可靠性的有效途径,具有重要的现实意义.关于齿轮故障诊断的研究目前已经取得一定的成果, 但是卫星系统的齿轮故障诊断尤其要求更加准确的精度,需要进一步探索更加有效的诊断算法模型,能精确发现故障模式并给出合理解决方案, 避免造成事故和经济损失[3−4].
目前国内外针对齿轮的故障检测方法有很多种,一般可归纳为基于信号、基于模型和基于数据驱动等3 种类型. 基于信号的检测方法是根据信号参数,利用小波变换、频谱分析等技术得到信号的属性特征, 通过对比分析实现故障检测. 例如:冯志鹏等提出的自适应多尺度线性调频小波分解方法, 有效识别出了行星齿轮箱故障特征频率[5]; 吴英建等采用多尺度模糊熵(multiscale fuzzy entropy,MFE)的特征提取算法,不需要齿轮箱的先验知识,能从强背景噪声中提取故障信息[6]; 刘林密等通过对齿轮振动信号进行经验模态分解(empirical mode decomposition,EMD)得到多个不同分量,再应用经验调幅-调频分解及傅里叶变换得到纯调频信号差分包络谱, 进而对断齿的振动信号实现了有效检测[7]. 基于模型的故障检测方法根据专家经验或者相关统计学知识,建立对应故障数理模型, 从而得出故障检测的各种规则和模式. 例如: 杨秀芳等釆用隐马尔科夫模型分析齿轮箱振动信号, 提取信号在时域、频域和时频域的统计特征, 训练了一组全特征- 隐马尔科夫模型库, 结果对齿轮正常、断齿的识别准确率高达97.9%[8]; Badihi 等引入模糊模型技术, 采用自动信号校正算法, 在风湍流、测量噪声和实际故障情况下进行不同的仿真, 实现了对风电场的故障检测[9];Harirchi 等提出一种基于时变参数不确定性隐式切换仿射模型的故障检测方法,引入了T-可检测性和弱可检测性概念, 使得模型失效算法可以在不影响检测结果的情况下以一种后退的方式实现[10]. 基于数据驱动的故障检测方法依托海量数据, 采用人工智能的各种算法, 在满足特定任务需求上挖掘探索故障的内在规律与联系.例如,刘剑生等、吴春志等提出了一种基于深度学习的强抗噪性故障诊断模型,先将齿轮箱训练集正常状态下样本的频谱信号进行排列和置零处理, 然后输入到由多种移动步长卷积核组合的多尺度卷积神经网络中进行训练, 实验取得了精确率和召回率的调和平均值为98.6%的良好效果[11−12]; 张阳阳等利用概率神经网络对齿轮箱进行故障诊断,在识别典型故障上比BP 神经网络拥有更高的准确率和诊断速度[13];鲁炯等提出一种将BP神经网络与D-S 证据理论相结合的风电轴承故障诊断方法,指出随着融合信号维度的增加,最终诊断结果的准确率也逐步提高[14]; 陈仁祥等提出一种深度置信网络迁移学习的齿轮故障诊断方法, 克服了神经网络需要大量训练样本的缺点,并取得92.82%的故障识别准确率[15].
由此可见,基于信号的检测方法简单快捷,易于实现,但无法挖掘深层次故障信息,无法识别潜在故障;基于模型的方法可以挖掘故障本质,使故障检测更具解释性,但难以建立完整、精确的数理模型,模型可移植性往往不佳; 基于数据驱动的方法无需检测对象的数学模型, 从数据出发, 让数据“说话”, 能挖掘得到数据背后的有价值知识[16], 专家系统、神经网络和模糊理论等人工智能算法在一定条件下能够获得较好效果, 但也都有各自的缺陷, 如专家系统推理效率低、缺乏有效的诊断知识, 神经网络对训练样本的需求较高, 模糊理论需要先验知识等.为此, 采用单一的故障检测技术常会出现结果精度不高、泛化能力弱等不足, 当前故障检测方法已经从过去单一信号分析、模型分析或深度学习向混合智能故障检测方向发展. 潘礼正等提出了基于小波包(wavelet packet,WP)与独立成分分析(independent component correlation algorithm, ICA)相融合的特征提取及SVM(支持向量机)相适配的故障诊断方法,相较于决策树和神经网络等其他方法, 其具有更高的分类准确率[17]; 章翔峰等利用S 变换处理原始信号并按照能力分布进行特征提取,结合SVM 实现对齿轮的故障诊断, 所提方法可以有效地降低噪声的影响[18]; 何雷等提出了一种将噪声辅助分析法、局部均值分解(local mean decomposition,LMD)及BP神经网络相结合的齿轮故障诊断方法, 诊断准确率为92.5%[19].
综上所述, 由于齿轮的振动信号存在非线性及非平稳性的特点, 因此, 对齿轮故障诊断的关键是如何提取其振动信号的特征. 常用的信号处理方法是傅里叶变换及小波变换, 小波变换虽能揭示非平稳信号的局部特性, 但在高频部分的分辨率较差. 小波包变换虽然弥补了小波变换的缺陷, 但在信号的分解及重构过程中存在较为严重的频率混叠问题[20]. 双树复小波包(dual-tree complex wavelet packet transform,DT-CWPT)是对小波变换及小波包变换的延伸,它具有近似平移不变性、完全重构性以及频率混叠小的优点[21]. 双树复小波包变换已被应用在轴承的故障诊断上[22],因此,基于双树复小波包分解的良好性能, 提出利用双树复小波包对齿轮故障信号进行分解,再对其进行特征提取.
支持向量机是一种以统计学为理论基础的机器学习算法, 其具有良好的推广能力及强大的非线性处理能力. 相比于人工神经网络,支持向量机克服了需要大量数据样本或者经验知识的缺点. 在工程实际中,获得大量的故障数据也较为困难,尤其是对卫星系统的在役考核,故障数据的获取更是相对不易.而支持向量机是基于结构风险最小化的机器学习算法,适合处理小样本数据,而且被广泛地应用于故障诊断当中[23]. 卫星系统在役考核过程中,针对卫星工作电磁环境非常复杂, 齿轮故障检测必须满足精准高效这一要求,因此,提出了能全面分解提取和保留齿轮信号特征的双树复小波包与对样本量需求相对较小的支持向量机算法相融合的检测模型, 并在公开数据集上进行实验和效果对比验证.
1 相关理论
1.1 双树复小波包变换原理
传统离散小波包变换在对原始信号进行分解时,采用下抽样的方式, 每次信号分解后的采样率降为原来的1/2,时间分辨率也降为原来的1/2. 分解层数确定后,频带的分辨率也随之确定,但时间分辨率却降低. 下抽样没有平移不变性的特性,并且会导致较为严重的频率混叠,对信号的奇异点也较为敏感.
针对传统小波包变换的不足,Bayram 等提出了双树复小波包变换, 双树复小波包变换是基于双树复小波对其进行的改进[24]. 双树复小波包变换在对信号进行分解与重构时,采用的是两组平行的低、高通滤波器的离散小波包构成的, 可视为实部树与虚部树, 这样在信号的分解与重构过程中可使信息互补. 双树复小波包变换的两层分解及重构过程示意图如图1 所示.
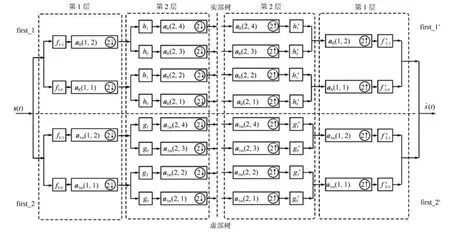
图1 双树复小波包两层分解及重构示意图Fig.1 Schematic diagram of two-layer decomposition and reconstruction of dual-tree complex wavelet packet
图中,s(t)代表原始信号, ˆs(t)代表重构后的信号,firs −1 代表实部树的滤波器组,f1−0代表低通滤波器,f1−1代表高通滤波器; firs −2 代表虚部树的滤波器组,f2−0代表低通滤波器,f2−1代表高通滤波器.当分解层数大于2 时, 为保证两树在当前层及所有前层的延迟差总和相对于原始信号为一个采样周期,实树部交替采用Q_shift 滤波组h, 虚数部交替采用Qshift 滤波组g.aR表示实树部的各层分量,aIm代表虚树部的各层分量. 每层的分解中,使用系数二分的方式,可以提高分解效率.信号的重构中,带“”的量代表重构过程采用的滤波器, 重构过程是分解过程的逆过程.
1.2 支持向量机
二分类支持向量机的主要思想可以简单表示为图2 所示的分类示意图,正方形表示第1 类样本,三角形表示第2 类样本.H代表分类线,H12分别表示与H平行的直线,与此同时H12也要经过两类样本离分类线最近的样本,H12之间的距离为分类间隔.其中的分类线可以把两类样本正确地分开, 使分类间隔最大的分类线称为最优分类线.
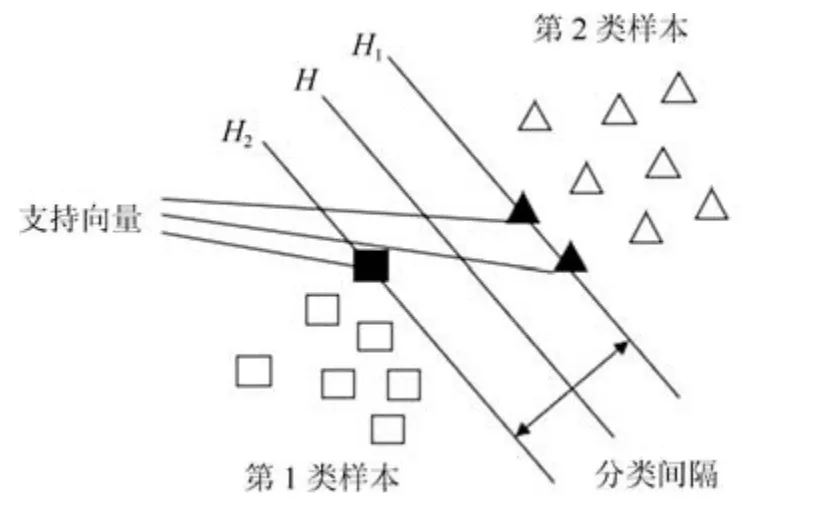
图2 二分类示意图Fig.2 Schematic diagram of two categories
设分类线平面方程如下:

设线性可分的样本集(xi,yi)(i=1,2,···,n),其中,x∈Rd,y∈{−1,1};满足下述条件:
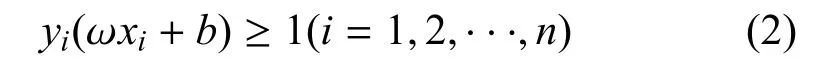
针对齿轮的故障类型识别是一个多分类问题[25−26], 故而可以把一个多分类问题转化为二分类的问题.训练时将其中的某一个类视为一个类别,其余的视为另一个类别, 形式上与二分树结构图类似,多分类示意图如图3 所示.
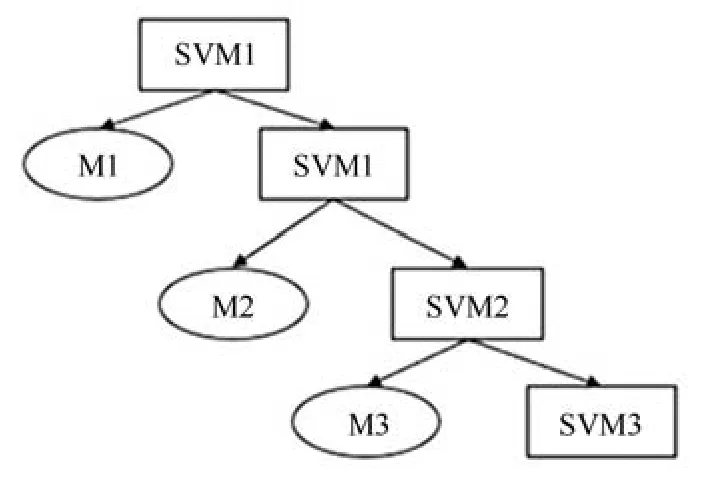
图3 多分类示意图Fig.3 Schematic diagram of multiple classificatio
1.3 主成分分析
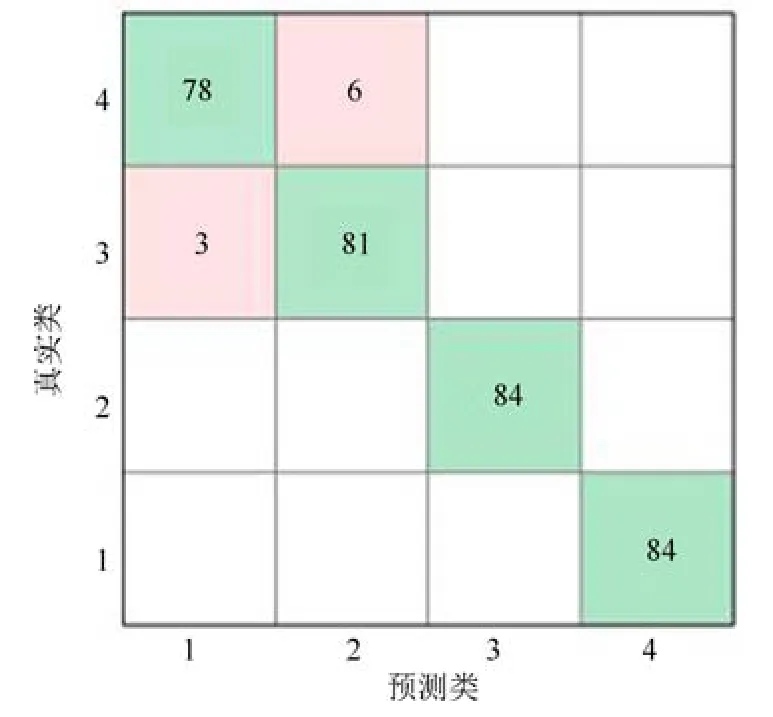
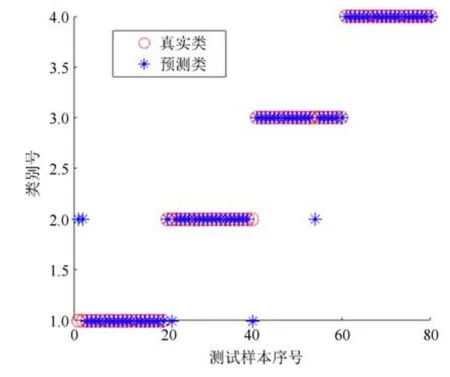
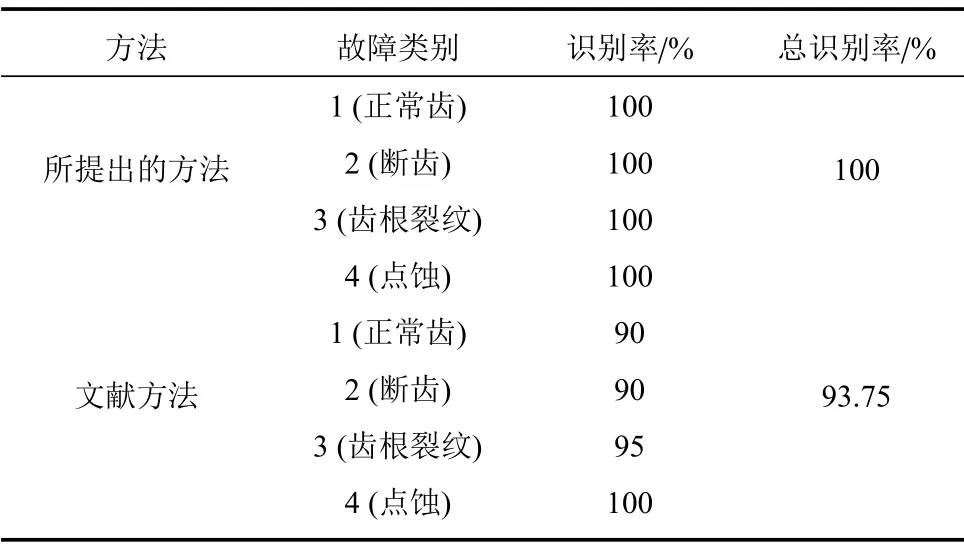
主成分分析[27](principal component analysis,PCA)的核心思想是在原始数据的n维向量中找到k(k PCA 算法主要步骤如下: 假设有m个n维样本,要将其降为k维数据. 1)把原始数据做成一m×n矩阵XXX; 2)计算X每列的均值,每列元素减掉该列的均值,得到新矩阵XXXc,其转置矩阵为 4)计算CCC的特征值及相应特征向量; 5)依据特征值大小, 按从大到小的顺序排列对应的特征向量,并取前k列构成矩阵PPP; 6)计算Y=XXXcPPP,则Y即为降维后的数据. 原始信号经过双树复小波包变换后得到一系列子信号,然后对子信号进行特征提取. 利用主成分分析对特征向量进行降维. 最后将降维后的特征集作为输入, 输入到SVM 中进行齿轮故障诊断. 所提齿轮故障诊断方法的流程图如图4 所示,步骤如下: 图4 齿轮故障识别流程图Fig.4 Flow chart of gear fault identificatio 1)对原始信号进行DT-CWPT 分解,设定分解层数为m,则子信号个数为2m; 2)对子信号进行特征提取; 3)用主成分分析特征向量进行降维; 4)将降维后的特征集分为训练集和测试集, 把训练集输入到SVM 中进行训练; 5)将测试集输入到训练好的模型中进行测试,计算故障识别率. 使用数据样本取自康涅狄格大学机械工程学院的PEI CAO 等收集的齿轮箱故障数据集. 取正常齿及3 种典型故障(断齿、齿根裂纹、点蚀)的数据进行研究,每类故障(包括正常齿)有104 个样本,每个样本包括3 600 个数据点. 4 类故障的原始数据如图5 所示. 图5 原始数据Fig.5 Raw data 设xi为时域信号的幅值,其常用时域特征如表1所示. 表1 信号时域特征Table 1 Signal time domain characteristics 实际应用中常用的小波基函数包括dbN 和symN 系列, 结合齿轮信号去噪与光滑等需求的特点,实验中采用db3 小波基函数. 原始信号经过3 层DT-CWPT 分解后得到8 个子信号,1 个子信号可以提取7 个特征,8 个子信号共56 个特征,将每个子信号特征依次排成一行,这样便构成一个行向量,即样本的特征向量. 4 类样本的特征如图6 所示. 由图6 可知,4 类样本之间的特征幅值相差较大,尤其是齿根裂纹,其次是点蚀. 从齿根裂纹和点蚀这两种故障模式本身的数据特征上看, 由于不同样本齿根裂纹和点蚀的损伤程度本不一致, 例如齿根裂纹长短和裂隙深浅必定存在着较大差异, 点蚀的蚀孔直径大小和深度(点蚀系数)必定也客观存在较大差异, 故而表现出其特征相应的数据取值存在着较大的幅值差异.若不对数据进行归一化,分类特征将很不明显,归一化之前的特征如图7 所示. 图6 4 类样本特征图Fig.6 Four types of sample feature map 图7 未采用归一化降维局部放大Fig.7 Features without normalization dimension reduction 为消除特征之间的差异带给最后诊断的影响,因此,需要对特征进行归一化,归一化处理后的特征如图8 所示. 图8 归一化后的特征Fig.8 Features after normalization 归一化后的数据, 每个样本仍然包含56 个特征. 为避免带来“维度灾难”,需要对数据进行降维处理. PCA 是一种常用的线性降维方法, 它能够尽可能多地保留原数据的信息. 通常选择累计贡献率大于等于85%的前K个主成分进行分析.通过实验发现, 经PCA 降维后的前面11 个主成分累计贡献率为85.48%. 其贡献率依次分别为: [49.29%, 9.92%,5.73%,3.88%,3.46%,3.27%,2.66%,2.30%,2.03%,1.77%, 1.36%]. 选取前2 个主成分(累计贡献率为59.21%)和前11 个主成分的特征指标分别作为SVM 的输入,发现故障识别率均为100%. 故选择前两个主成分指标,并将数据进行可视化,经PCA 降维后的数据如图9 所示. 图9 PCA 降维后的时域特征Fig.9 Time domain characteristics after PCA 由图9 可知,4 类数据不存在相互交叉的数据点,能够被较好地区分. 但是同时发现, 点蚀与齿根裂纹、断齿与正常齿之间的类间距较小,为了增大其类间距,考虑尝试将信号的频域特性作为分类特征,包括常用的平均频率、重心频率、频率均方根以及频率标准差4 个频域特征,如表2 所示. 同样地,将原始信号经过DT-CWPT 分解为8 个子信号,每个子信号提取4 个特征,这样一个样本的特征向量就有32 维.经PCA 降维后前3 个主成分累计贡献率为90.34%,分别为[59.83%, 23.54%, 6.98%]. 选取前2 个主成分(累计贡献率为83.37%)和前3 个主成分的特征指标分别作为SVM 的输入,发现故障识别率也均为100%. 故选择前两个主成分指标, 并将数据进行可视化,经过PCA 降维后的数据如图10 所示. 表2 信号频域特征Table 2 Signal frequency domain characteristics 由图10 可知,点蚀与齿根裂纹的类间距明显增大,且内部聚集度也高于时域特征. 为进一步分析不同特征选取的效果, 再将时域特征及频域特征组合起来进行分析. 时域特征与频域特征共11 个特征,同样经DT-CWPT 分解后,一个样本的特征向量就有88 维, 经PCA 降维后的前面9 个主成分累计贡献率为86.07%,依次分别为:[54.42%,16.37%,6.46%,1.86%, 1.73%, 1.57%, 1.34%, 1.19%, 1.12%]. 选取前2 个主成分(累计贡献率为70.79%)和前9 个主成分的特征指标分别作为SVM 的输入,发现故障识别率仍然都为100%. 故选择前两个主成分指标,并将数据进行可视化,经PCA 降维后的数据如图11所示. 图10 PCA 降维后的频域特征Fig.10 Frequency domain characteristics after PCA 图11 PCA 降维后的时频组合特征Fig.11 Time-frequency combination after PCA 对比图10 与图11 可知,4 类样本的类间距变化不大,图11 中正常齿的内间聚集度明显变得分散.因此,选用频域特征进行后续分析. 将降维后的数据进行标记(正常齿标记为1、断齿标记为2、齿根裂纹标记为3、点蚀标记为4), 并将标记后的数据分为两个训练集, 随机抽取每类中的80%(84 个样本)作为训练集,剩余的20%(20 个样本)作为测试集. 为保证模型具有较好的泛化性能,将训练集输入到SVM 进行训练时采用5 折交叉验证法[28−29]. 核函数选择径向基函数(RBF),利用网格搜索法进行参数寻优, 得到惩罚系数C为0.021 66,σ 为5.645 2. 模型在训练集上的混淆矩阵如图12 所示,将测试集输入到训练好的模型中,预测结果如图13 所示. 为对比所提方法的优越性,采用文献[30]中的方法对数据进行处理, 模型在训练集上的混淆矩阵如图14 所示,预测结果如图15 所示. 图12 该方法混淆矩阵Fig.12 Confusion matrix of our method 图13 该方法预测结果Fig.13 The prediction results of our method 由图12 可知所提出的方法在训练集上没有被错分的类别,由图13 可知所提出的方法在测试集上的识别率为100%; 由图14 可知文献方法在训练集上有被错分的样本,图15 可知文献方法在测试集上第1, 2, 3 类均有识别错误的样本. 两种方法识别结果汇总如表3 所示. 图14 文献方法混淆矩阵Fig.14 Confusion matrix of literature method 图15 文献方法预测结果Fig.15 Forecast results of literature method 表3 2 种方法故障识别结果Table 3 Fault identificatio results of 2 method 由表3 可知,文献方法在第1,2,3 类及总识别率均没有所提出方法高. 针对卫星系统在役考核中的齿轮故障诊断问题,提出建立一种集合双树复小波包、主成分分析及支持向量机的综合算法模型, 充分利用双树复小波包分解良好的方向选择性及近似平移不变性等优点,采用该方法对原始信号进行分解更利于特征的提取;将信号特征提取的3 种方式(时域、频域、时频域结合)进行了实验对比分析,利用3 种特征提取方式的主成分综合指标,选取不同的维度分别作为SVM 的输入,发现其故障识别率均为100%. 由此可知,故障识别效果受PCA 降维之后的维度选择影响较小,充分说明采用的特征提取方法合理有效;因此,最终采用信号频域指标进行特征提取的特征向量维度最少,类间距清楚明显,内聚度也更高;通过公开数据集上的实验结果对比表明, 所提方法在准确率上拥有明显优势, 对故障的总识别率达100%, 为齿轮故障的精准识别提供了一种有效的新方法. 下步将研究如何实现在轨卫星在役考核中齿轮等组件的远程监测诊断和故障预测, 以及如何进一步改进优化当前模型,以提高故障诊断的效率.2 故障诊断步骤
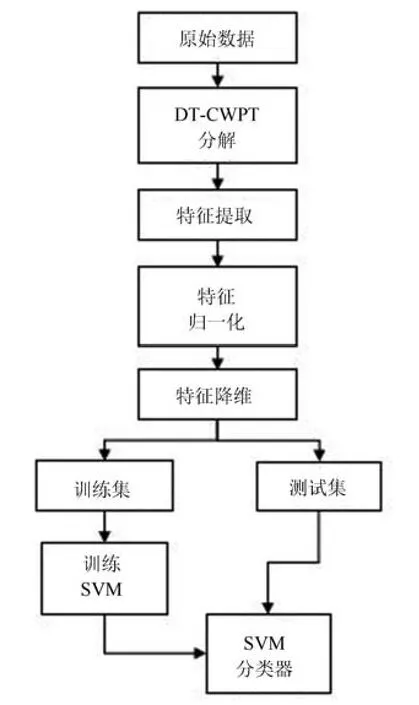
3 试验分析
3.1 样本陈述
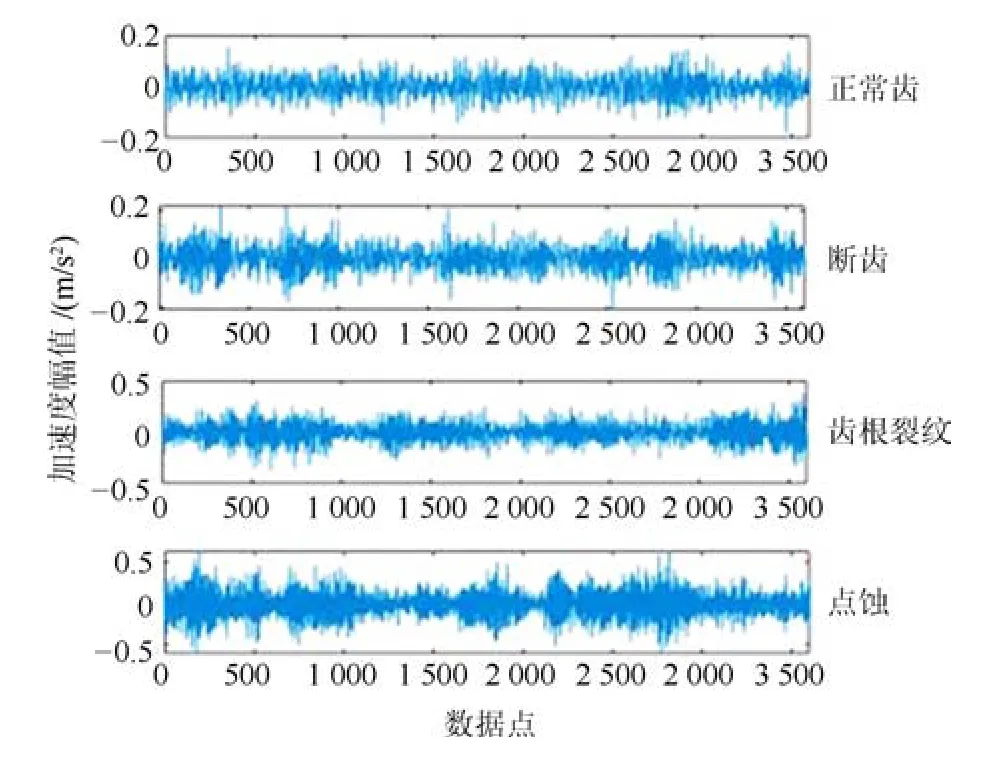
3.2 特征提取
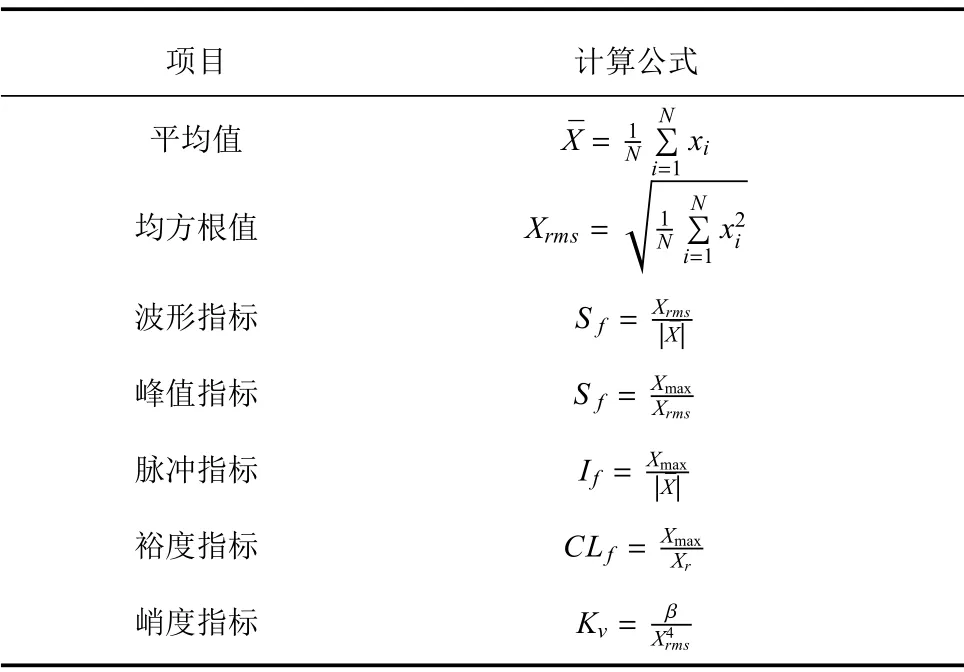
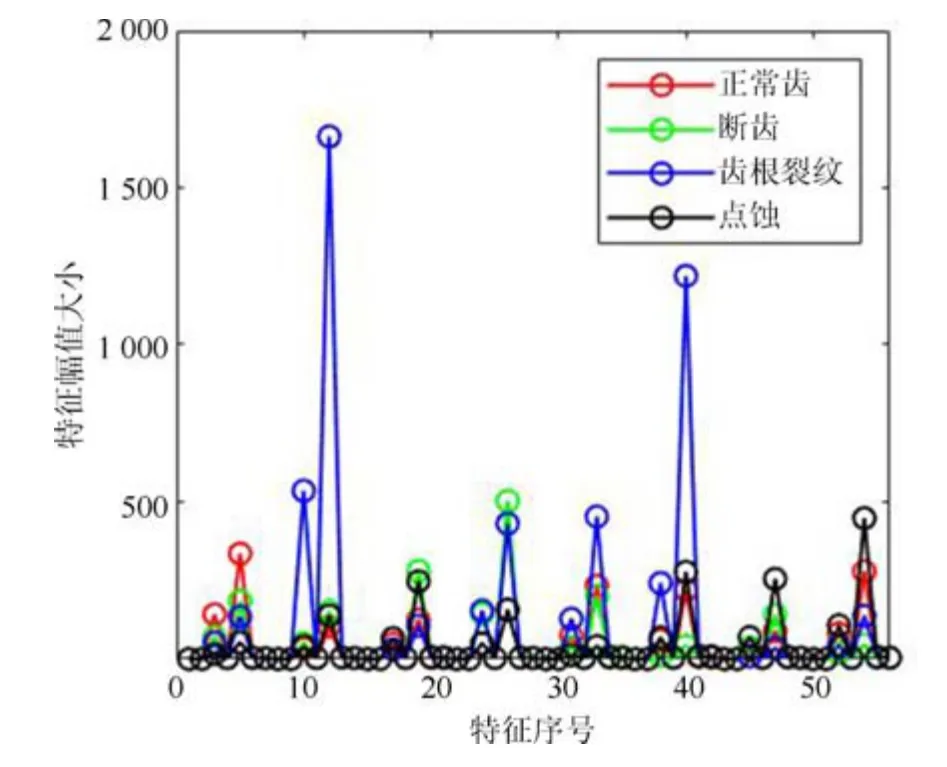
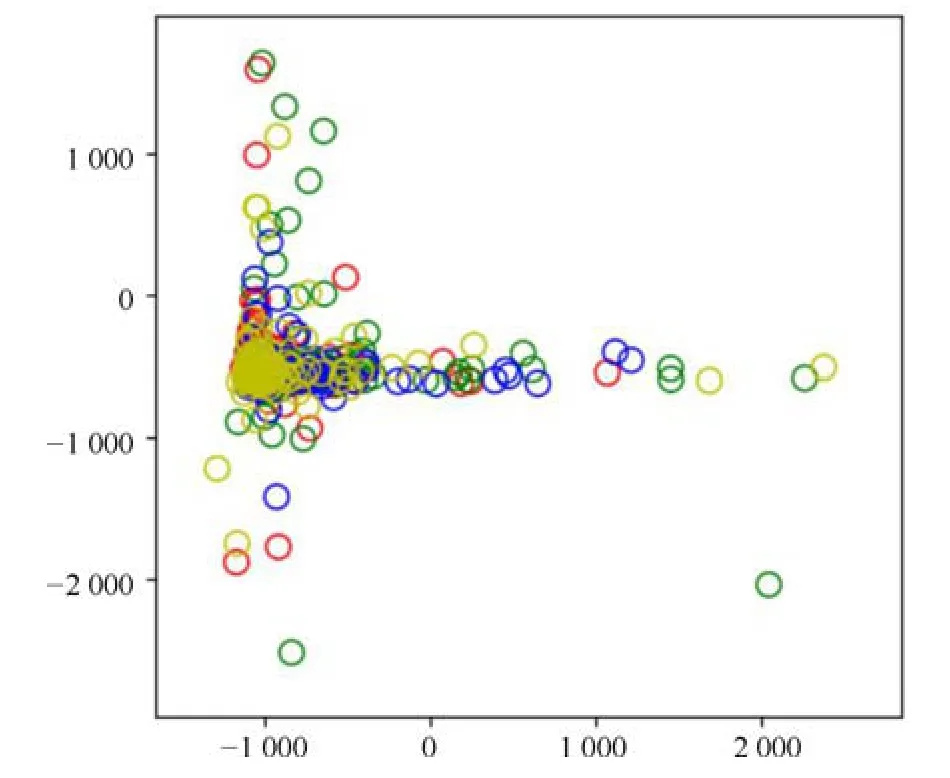
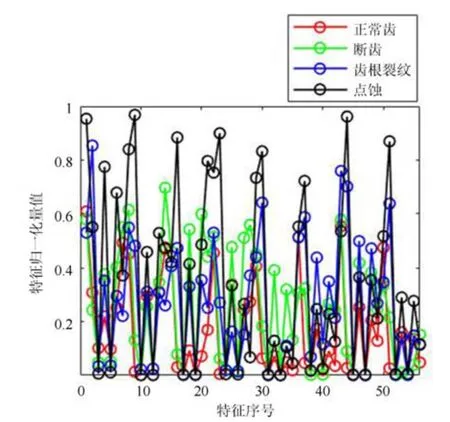
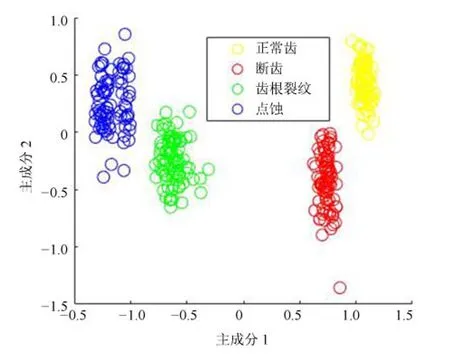
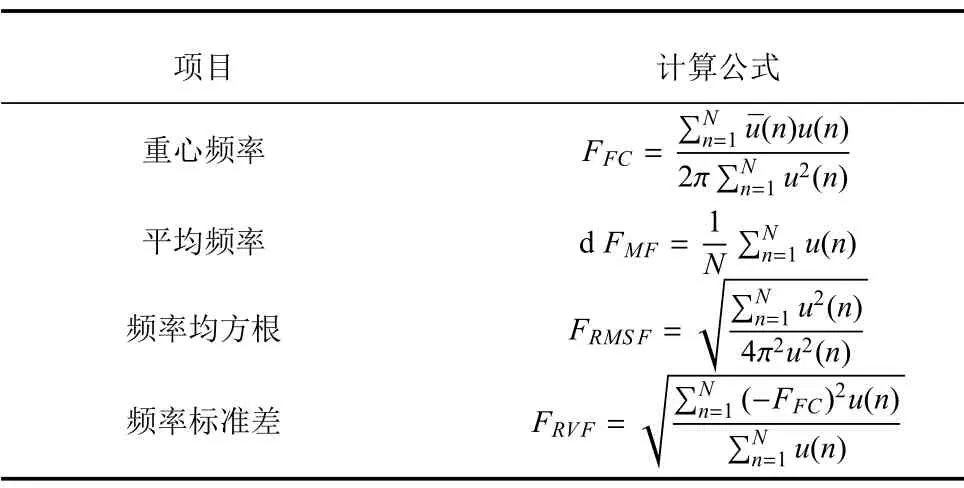
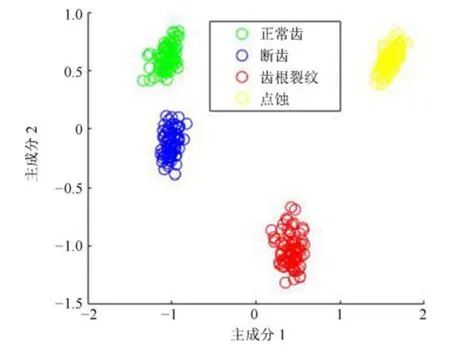
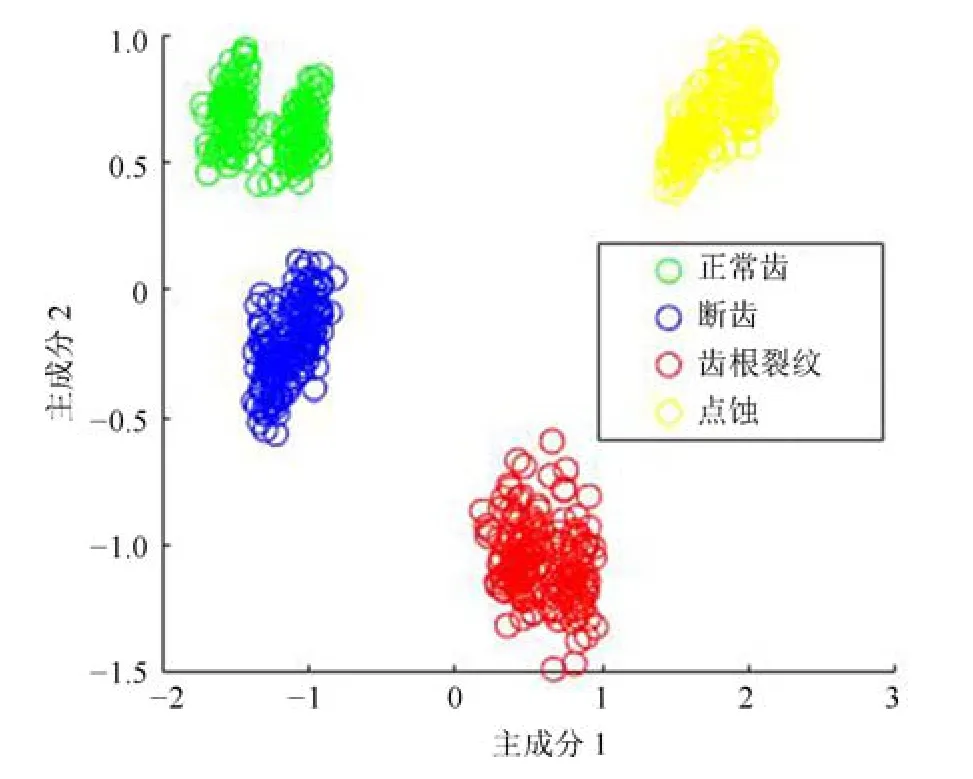
3.3 支持向量机分类
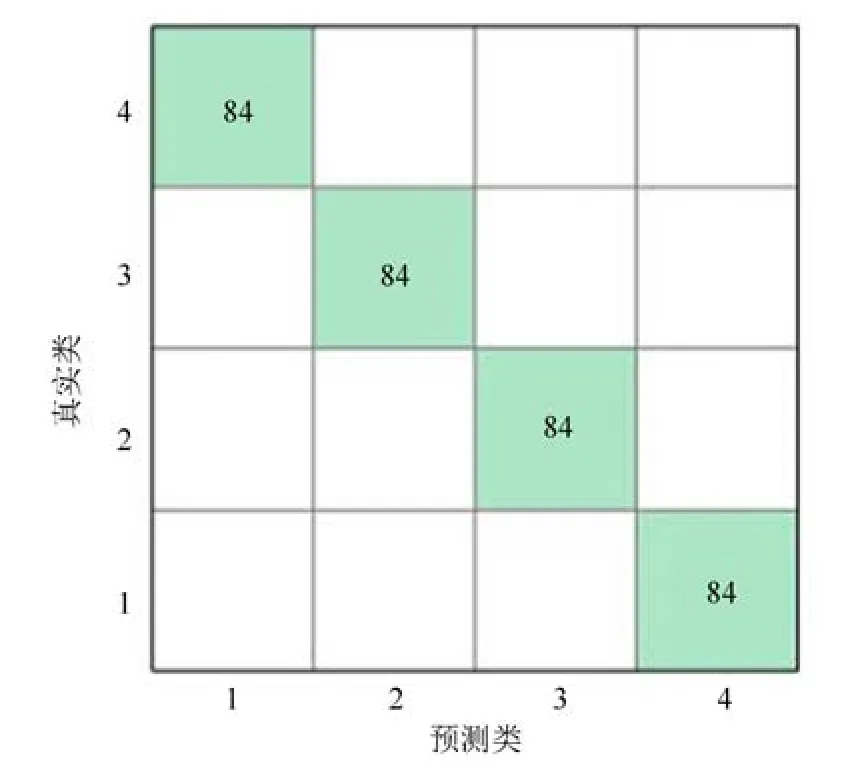
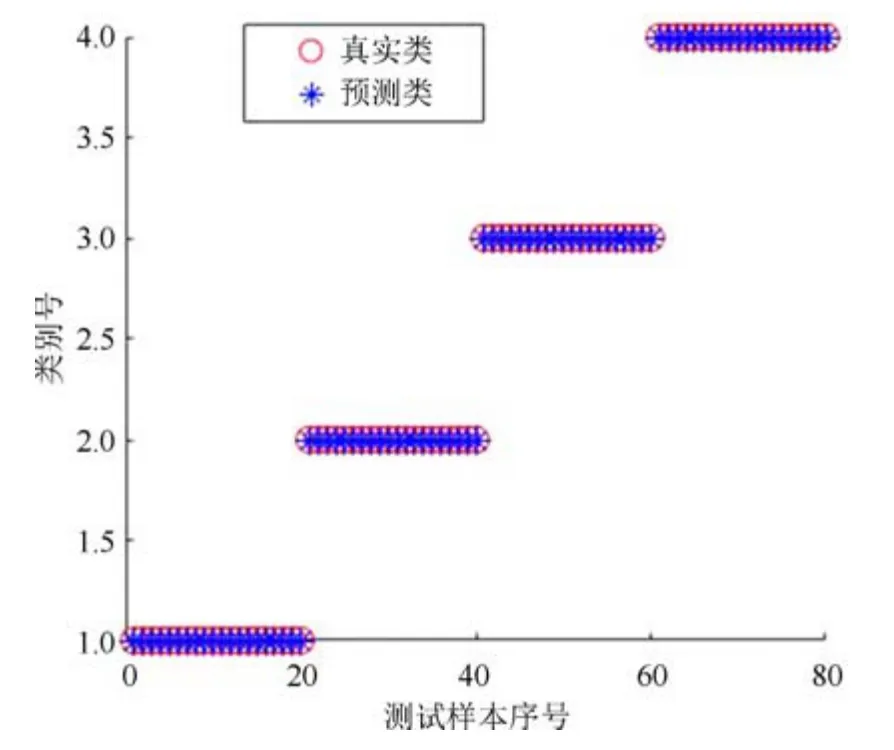
4 结论

