如何用“项目教学法”引导学生学习线性规划知识

刘佳婕

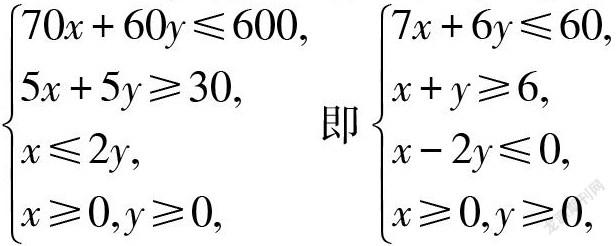
线性规划作为一种重要的数学模型，在经济、农 业、工业、交通等领域中有着广泛地应用.由于线性规划中涵盖的知识范围广，教学课时较少，如果采用常规的教学模式，学生很难在短时间内掌握其精髓，所以教师需调整教学方案，将项目教学法应用到线性规划教学中，让学生通过自主探索、动手实践和合作交流，掌握知识，提高解决问题的能力和实践能力.

一、设置项目任务

在教学线性规划时，教师要首先根据教学内容设置一个或几个项目任务，可从学生的生活实际入手，设置一些难度适宜的项目任务，也可以和他们一起讨论，确定项目的目标和任务.这样有利于调动学生的积极性，激发其学习兴趣.

例如，在教学“简单的线性规划问题”时，笔者设置了如下的项目任务：现电视台播放甲、乙两套连续剧，每次播放连续剧时，需要播放广告.已知每次播放甲、乙两套连续剧时，连续剧播放时长、广告播放时长、收视人次如下表所示：

已知电视台每周安排的甲、乙连续剧的总播放时间不多于 600 分钟，广告的总播放时间不少于 30 分 钟，且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.那么电视台每周播出甲、乙两套连续剧各多少次，才能使总收视人次最多？

该项目任务与学生的生活实际比较贴近，能快速调动他们的学习积极性，使其主动参与到项目研究中.

二、引导学生合作探究，制定项目方案

在布置好项目任务后，教师可按照学生的实际情况，将他们分为几个小组，组织他们以小组为单位进行合作探究，确定操作步骤和程序，制定出合理的项目方案.在整个教学过程中，需以学生为主体，以教师为主导，以便让学生通过研究项目掌握知识、锻炼能力.

仍以教學“简单的线性规划问题”为例，在布置项目任务后，笔者将学生分成3～4人一组的学习小组，在每个小组中选取一名学生作为小组组长，让其负责小组团队的组织与协调工作.学生根据所掌握的资料及已有知识经验制定项目实施方案，并讨论方案的可行性与合理性.其中一个小组讨论的情况如下.

生 1：若用 x，y 表示每周计划播出的甲、乙两套连续剧的次数，那么总收视人次为 60x+25y ，所以问题就是求“求 x，y 分别为多少时，60x+25y 的最大值”

生2：x，y满足的数学关系式为

我们可以将问题转化为关于 x 和 y 的二元一次不等式方程组问题.

生3：那我们该怎么求最大值呢？

生2：我认为可以用数形结合的方法，首先将不等式组的解集转化为平面区域内的点的集合.

生1：类似 z = 2x + 3y 的方程在平面直角坐标系中可以转化为一组斜率相等的平行直线.

生 3：那么这组平行直线中的 z 就表示直线的纵截距.

在讨论的过程中，学生首先根据项目任务想到了用数形结合法和转化思想来解决问题，将求最值的问题转化为在平面区域内，求一组斜率相等的平行直线的纵截距的最大值问题.这样学生通过深入探索，找到了解答线性规划问题的思路和方法，锻炼了思考和分析问题的能力.

三、展示项目成果

成果展示和评价是项目教学的最后一个环节，也是至关重要的环节.教师可以让学生以小组团队口头汇报、黑板演示或多媒体演示等多种形式展示团队的学习成果，分享学习经验，最后由教师对学生的学习成果进行评价.

在学生完成上述项目任务后，笔者让其中一个小组展示了他们的学习成果：

学生在分享的过程中能发现问题、提出新问题，进行深度学习，从而真正理解了线性规划问题的本质，同时在解决实际问题的过程中学会运用线性规划知识和数学建模思想来分析与解决问题.

综上所述，在线性规划教学中实施项目教学法，有利于帮助学生快速掌握解答线性规划问题的方法和思路，并使其学会运用数形结合思想和转化思想将不等式组问题转化为解析几何问题进行分析，这对于培养学生的综合运用线性规划知识和解决实际问题的能力具有十分重要的意义.

（作者单位：江苏联合职业技术学院徐州经贸分院）