尾矿坝振动实验数据样本容量的优化研究
刘振广, 徐正华, 廖茂新, 刘宏亮
(南华大学 数理学院,湖南 衡阳 421001)
0 引 言
尾矿是矿石经矿场筛选后剩余的砂状废弃物,尾矿逐渐堆积形成尾矿坝[1]。振动造成的尾矿坝结构变化是造成溃坝事故的重要原因之一。国内外对振动条件下尾矿坝稳定性进行了多方向的探索,有研究地震条件下尾矿坝事故的,有通过室内振动实验研究尾矿坝模型变化的,其中,KULALI[2]通过实验分析了不同土壤对氡析出的影响。蔡嗣经、张栋等[3]通过实验室振动实验研究了尾矿砂的动力特性。柳厚祥、廖雪等[4]研究了地震对尾矿坝裂缝水压变化的影响。陈存礼、何军芳[5]等研究了三轴实验中饱和尾矿砂动孔压变化规律。A.D.K.Tareen[6]等人通过运用箱线图对氡逸出率实时数据异常变化的检测,实现了基于氡析出率变化的地震预测方法。C.Bilibio[7]与S.Cockenpot[8]研究了温度对氡析出率的影响,得到氡析出率随温度升高而增加的规律。马宇艇[1]通过振动台系统研究了尾矿坝振动动力响应,得到尾矿坝变形破坏的基本趋势。
本文根据振动实验设计的需要,研究数据样本容量的优化度量方法。在实验数据总体统计特征已知的条件下样本容量可以根据统计学公式来确定[9];在实验数据特征未知的条件下,样本容量通常根据以往经验或相似实验来确定。振动实验中逸出氡累积浓度数据的特征具有未知性,按相似实验经验确定样本容量将造成实验数据失真或实验成本过高等问题。
本文在两种振动实验条件上,对实验数据集进行数据还原后抽样获得数据子集,对数据子集进行曲线拟合得到拟合方程,度量拟合方程对还原后数据集的代表能力,在满足实验精度要求的前提下得到实验较优优样本容量。
1 实验介绍与样本容量优化度量算法设计
1.1 实验数据采集与还原
尾矿坝振动模拟实验主要包括测氡仪、双向激振系统、逸出集氡模型试验箱、信号采集处理系统四部分组成。其中测氡仪用来测量氡浓度,激振系统用来对模型施加激振力,逸出氡模型实验箱用来收集逸出气氡,信号采集处理系统用来接收并显示振动与氡密度信号。在设定电压、电流及振动频率的条件下,通过对气氡浓度数据进行等距采样,设定采样间距为5 min,得到实验数据样本集B={(ti,yi)|i=1,2,…,36},其中,ti表示时间点,yi表示时间点对应的逸出氡累积浓度。
振动条件下微塑模型中,由于尾砂量有限,累积逸出氡累积浓度变化遵循气体扩散效应,初始阶段累积氡浓度大致呈线性趋势匀速增长,然后累积氡浓度增长速度递减而渐趋平稳。
实验条件的限制导致振动实验时间不够长,采集到的样本数据量较小,数据基本分布在逸出效应曲线的中前段。本文首先在实验样本数据与逸出效应规律的基础上,通过函数构造法对实际数据进行反演还原。本文选取偏向角均值递减方法对两种振动条件下的实验数据集进行还原,得到振动条件下累积氡浓度数据集D={(ti,yi)|i=1,2,…,n}。
本文构造了偏向角均值递减的数据还原方法,利用数据集B中数据偏向角的变化规律,通过计算偏向角均值并使偏向角按均值递减,推导还原出实验未能得到的逸出氡累积浓度值。
设
(1)
即θi表示数据集B中的倾斜角[10]。
令
(2)

设还原数据偏向角按照均值递减,可得
(3)
由偏向角均值递减可推导得到
yi=yi-1+(ti-ti-1)tanθi-1,i=37,38,…,n。
(4)
对还原后实验数据集绘制散点图,如图1和图2所示,图1中电压为3 V、电流为1 A、振动频率为10 Hz的条件下逸出氡累积浓度随时间变化趋势散点图;图2中电压为3 V、电流为2 A、振动频率为30 Hz的条件下逸出氡累积浓度随时间变化趋势散点图。
1.2 确定最小样本容量


图1 振动条件为3 V-1 A-10 Hz时氡累积浓度变化散点图Fig.1 Scatter plot of the cumulative density of radon when the vibration is 3 V-1 A-10 Hz
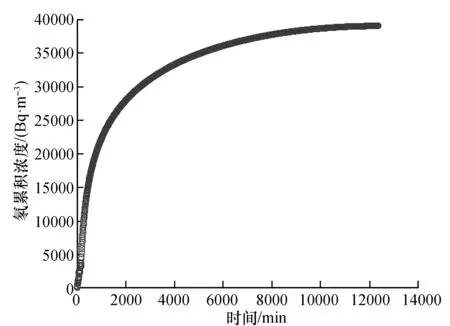
图2 振动条件为3 V-2 A-30 Hz氡累积浓度变化散点图Fig.2 Scatter plot of the cumulative density of radon when the vibration is 3 V-2 A-30 Hz
1.2.1 随机起点等距抽样
等距抽样又称为系统抽样,是将总体平均按一定顺序分为若干部分,随机确定起点后分别从各部分中抽取数据形成样本子集S。等距抽样适用于总体数据具有一定稳定变化趋势的情况,可以保证所抽取的样本代表性较好[11]。本文应用随机起点等距抽样方法对还原后实验数据集D进行抽样,在不同采样间距下得到样本子集S={(xj,cj)|j=1,2,…,m}。
设l为采样间距,其中l=5,10,…,5k,k∈Z,则样本容量m为
(5)

算法1.1 随机起点等距抽样算法
步骤1输入还原后数据集D={(ti,yi)|i=1,2,…,n}和采样间距l,(l=5,10,…,60);
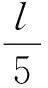
步骤3顺序抽出数据集D编号为i1,i1+l/5,…,i1+(m-1)l/5的元素,则样本子集S中元素(xj,cj)=(ti1+(j-1)l/5,ci1+(j-1)l/5),1≤i1≤l/5,j=1,2,…,m;
步骤4输出样本子集S={(xj,cj)|i=1,2,…,m}。
在不同采样间距下抽取出不同样本容量的数据样本,下面给出不同样本最小二乘拟合与拟合效果评价的方法。
1.2.2 反正切型函数最小二乘估计
在还原后数据集图像中,图像先线性上升然后上升速度渐缓最终比较平稳,实际数据分布如图1和图2所示。
由图1和图2图像可以观察到数据集D与反正切型函数图像相似,因此本文采用反正切型函数模型对抽取出的样本子集S进行拟合,得到不同样本子集对应的拟合方程。
设反正切型函数回归方程为
y=a+b×atan(c×x),
(6)
式中a,b,c为待定参数,待定参数需要通过样本数据估计得到。

(7)
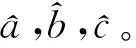
曲线拟合优度通常使用决定系数R2来表示[13],即
(8)

(9)
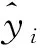
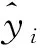
1.3 样本容量优化度量算法设计

算法1.2 样本容量优化度量算法
步骤1输入还原后数据集D={(ti,yi)|i=1,2,…,n};
步骤2绘制数据集D散点图,匹配反正切型函数拟合模型y=a+b×atan(c×x);
步骤3从数据集D中采集元素组成数据样本子集S;
步骤3.1 调用算法1.1;
步骤3.2 输出样本子集S={(xj,cj)|j=1,2,…,m}。



2 数据分析



表1 振动条件为3 V-1 A-10 Hz时不同样本容量的Table for different sample sizes when the vibration is 3 V-1 A-10 Hz

表2 振动条件为3 V-2A-30 Hz时不同样本容量的样本判定系数Table for different sample sizes when the vibration is 3 V-2 A-30 Hz
3 结果与讨论



