基于模型参考自适应的球形机器人运动控制①

余晨雨 章 政 郭庆瑞 张舰栋 金 震

(*武汉科技大学机器人与智能系统研究院 武汉430081)

(**武汉科技大学冶金自动化与检测技术教育部工程研究中心 武汉430081)

(***武汉科技大学信息科学与工程学院 武汉430081)

0 引言

球形机器人是一种具有封闭球形外壳、一体化机械结构的移动机器人,其驱动方式主要有质心偏移驱动、动量轮驱动和电机直接驱动等方式。相比于传统的轮式、履带式移动机器人,球形机器人具有全封闭、运动灵活、平衡能力及自我恢复能力强等特点,在星球探索、危险环境探测等领域具有显著优势和广泛的应用前景[1]。

球形机器人是一个典型的欠驱动、非链式、强耦合和非线性的复杂系统,由于其独特的机械结构和行走方式,导致球形机器人的机理模型存在结构复杂、参数不确定等问题,因此运动控制一直是球形机器人领域研究重点之一。文献[2]在非完整约束的条件下,分别建立球形机器人的运动学和动力学模型,通过输入变换将动力学模型变换为一个两输入的二阶系统,并基于非线性滑模控制方法分别设计了横向姿态控制器和纵向速度控制器,保证被控系统的运动状态收敛到期望的邻域。文献[3]基于动力学模型设计了一个状态反馈控制器,利用李雅普诺夫定理验证了控制率的稳定性,并通过外壳跟踪预期角速度函数来使机器人完成预期运动。文献[4]研究了球形机器人在坡面上的建模和运动控制问题,利用拉格朗日方程建立了系统的动力学模型并通过比例积分微分(proportional-integral-derivative,PID)控制器实现了球形机器人在坡面上的稳定控制。上述控制方式在一定程度上保证球形机器人稳定控制。然而,由于球形机器人环境感知能力不足,易受外部和内部的不确定性因素影响,导致球形机器人的运动参数变化大。因此,依赖准确性模型进行控制系统设计的方法存在一定的局限性,特别是当系统受到较大的干扰时,系统的控制效果将大大降低。

模型参考自适应控制(model reference adaptive control,MRAC)能够有效解决系统模型参数变化导致控制效果下降的问题,使系统获得较好的控制性能[5]。本文以自主搭建的球形机器人为被控对象,设计并实现了一种基于MRAC 的球形机器人运动控制系统。首先,采用拉格朗日方程建立球形机器人的动力学模型;然后,根据球形机器人的性能参数和运动过程信息,设计了模型参考自适应控制系统,按照李雅普诺夫稳定性理论设计自适应控制率,使系统的控制效果得到优化;最后,实验验证了本文所设计的基于MRAC 的球形机器人系统的可行性和有效性。

1 球形机器人的动力学模型

1.1 球形机器人结构设计

本文搭建的球形机器人实验平台由球形外壳、驱动平台和全向轮组成,外观和驱动平台结构如图1所示。

图1 球形机器人

图1 中,球壳为亚克力透明球,球壳内部是由三个互成120 °分布的全向轮和控制全向轮转动的驱动平台组成;全向轮采用直角电机驱动,其额定电压为12 V,转速为120 r/min;主控芯片采用的是RT1064;基于捷联惯性测量单元(intertial measurement unit,IMU)设计了姿态检测传感器,其中磁力计采用IST8310 传感器,加速度计和陀螺仪为MPU6050 整合性六轴姿态传感器。

球形机器人主要硬件参数数据如表1 所示。

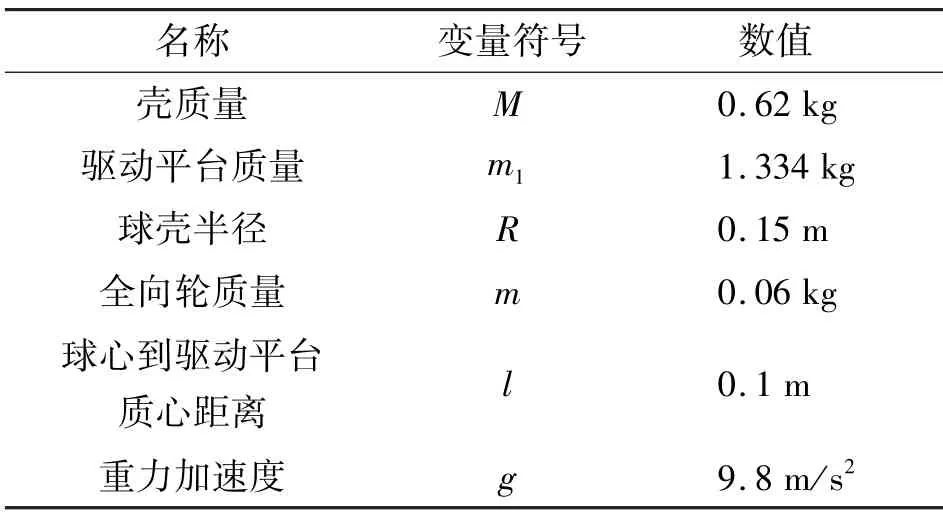
表1 主要硬件参数

1.2 系统建模

为了便于进行动力学分析,本文对球形机器人进行如下简化和假设。

(1) 由于球形机器人为轴对称结构且全向轮与球壳内壁相切,在进行直线运动时,将3 个全向轮直接等效为1 个驱动轮,驱动轮质量m2与全向轮质量m的关系为m2=3m。

(2) 考虑到驱动平台质量主要集中在电机和电池部分,在实际安装过程中,电机和电池主要集中在全向轮中心附近,因此将驱动轮半径等效为(R -l)。

(3) 球形机器人所有运动部件均为刚体。球形机器人在运动中无滑动摩擦,球壳与地面的滚动摩擦可以忽略不计。

(4) 球形机器人外壳等效为一个半径为R、质量为M的薄壁球壳。

当球形机器人沿直线运动时,其简化模型如图2所示。图2 中,OXY为固连于球形机器人初始位置地面的正交坐标系。设x为球形机器人球心位移,θ为内部驱动平台摆角,τ为驱动电机输出力矩。

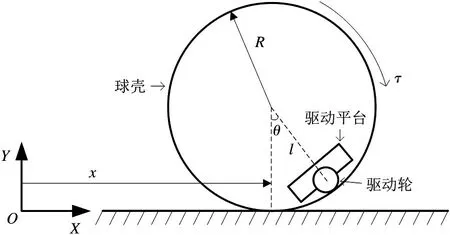
图2 球形机器人简化模型

由于球形机器人球心位移x和内部驱动平台摆角θ唯一确定,因此选取广义坐标变量为

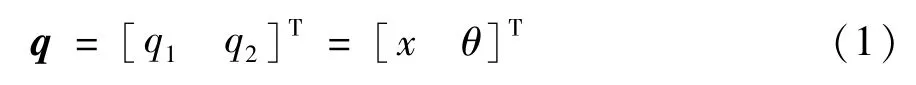
球形机器人球壳、驱动平台和全向轮产生的动能分别为

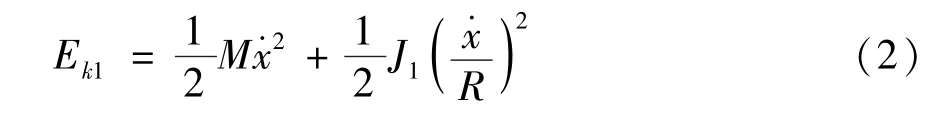
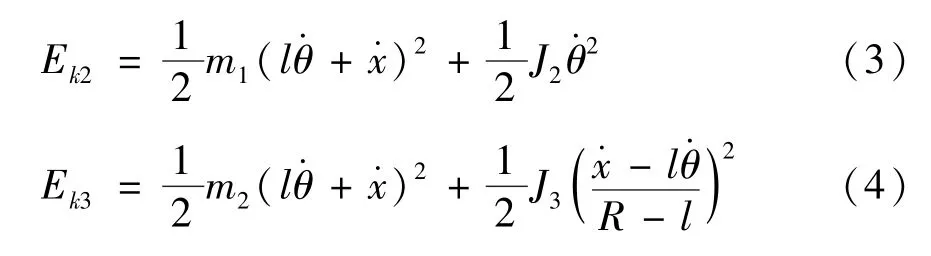
式中,J1为球壳转动惯量,;J2为驱动平台转动惯量,J2=ml2;J3为驱动轮转动惯量,J3。

选取地面为零势能点,球壳、驱动平台和全向轮产生的势能分别为

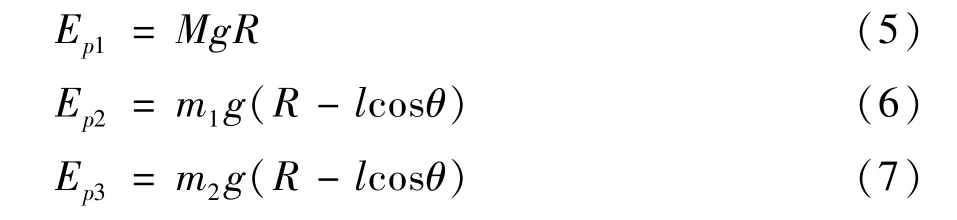
因此,球形机器人系统的拉格朗日函数L为

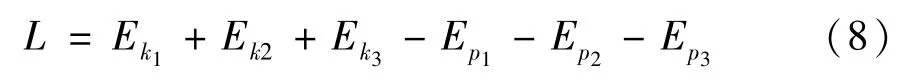
根据虚功原理,可得球形机器人系统所受的广义力Q为

拉格朗日方程的一般形式为

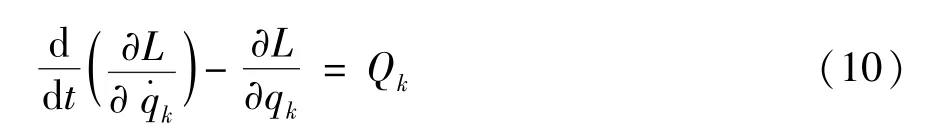
式中,qk为广义坐标q的第k个分量,Qk表示广义力Q的第k个分量。

将式(5)～式(9)代入式(10)得到球形机器人系统的动力学方程:

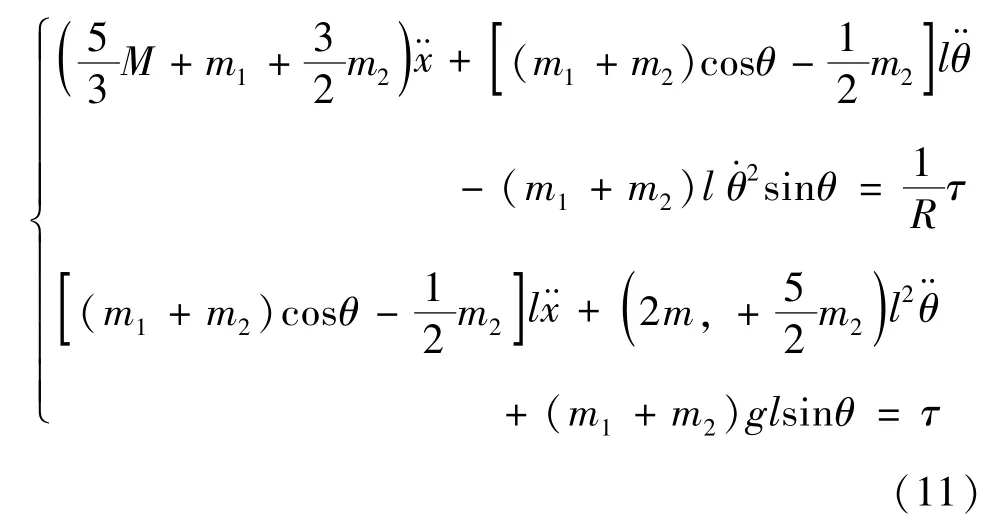
当球形机器人稳定运行时,球形机器人运动加速度和驱动平台摆角变化均很小,即都很小,此时内部驱动平台摆角θ满足:

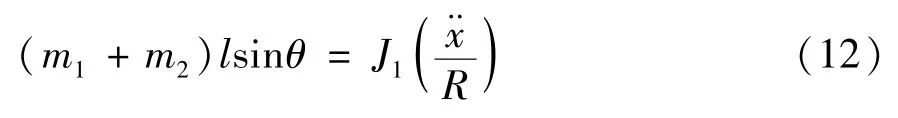
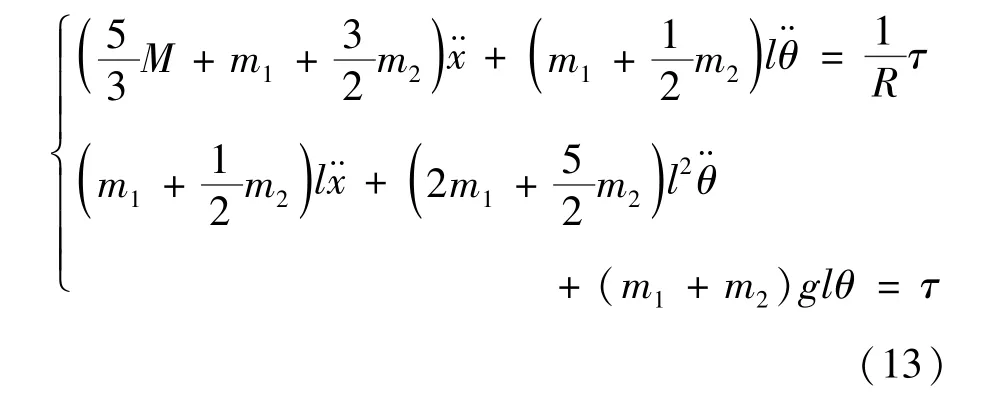
将式(13)表示为关于广义坐标q的二元二阶方程形式,则球形机器人动力学方程为

式中:

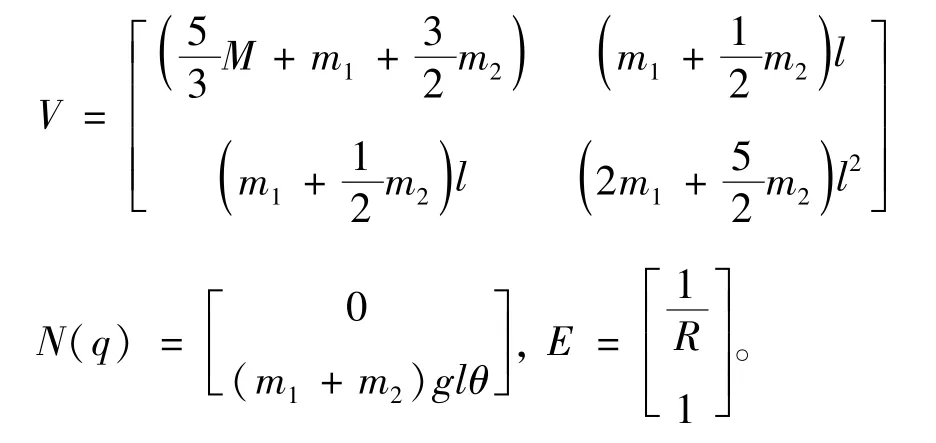
式中,A为系统矩阵,,B为输入矩阵,B=[0b10b2]T,C为输出矩阵,C=,[g1g2]T=-V-1N(q),[b1b2]T=V-1E。

2 模型参考自适应控制系统设计

由于球形机器人系统较为复杂,不能精确建立其系统模型,且在球形机器人运动过程中,系统模型参数可能发生变化,常规依赖于被控对象模型的控制算法将会产生误差,控制效果不能达到预期[6-12]。因此本文采用模型参考自适应控制算法对球形机器人系统进行运动控制,以取得较好的控制效果[13-15]。

本文搭建的基于MRAC 的球形机器人控制系统框图如图3 所示。图中,为参考模型,G和F分别为被控系统的前馈增益矩阵和反馈增益矩阵。当球形机器人模型参数发生变化时,系统输出y与参考模型输出ym之间会产生误差e,自适应机构将利用误差来对G和F进行动态调整,从而使被控系统能够实时跟随参考模型。

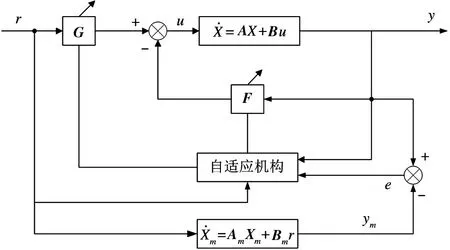
图3 基于MRAC 的球形机器人控制系统框图

2.1 参考模型选取

参考模型是系统期望的输出响应,因此参考模型的选取影响着系统的动态性能,本文采用极点配置的方式设计球形机器人的参考模型。根据式(15)所示的球形机器人状态空间模型,设期望的极点为s1、s2、s3和s4,对应系统模型的反馈向量为K,则球形机器人的参考模型为

2.2 自适应机构设计

在模型参考自适应控制中,利用李雅普诺夫方法设计自适应机构能够保证系统具有全局渐进稳定性,且该方法已经得到广泛使用[16]。本文基于李雅普诺夫方法设计球形机器人的自适应机构。

由图3 可知,引入前馈增益G和反馈增益F后,球形机器人的状态方程为

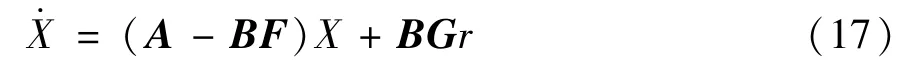
根据式(16)可知,被控系统和参考模型输出矩阵为单位向量,因此:

那么广义误差的状态方程为

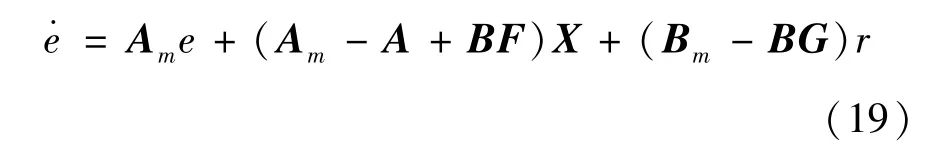
设G和F的理想值分别为,则当和时,满足:

则由式(19)可得:

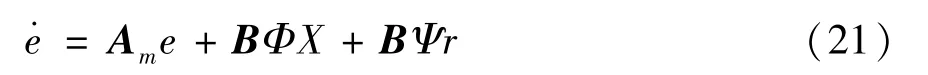
在以广义误差e与可调参数误差Φ和Ψ组成的增广状态空间中,定义李雅普诺夫函数为

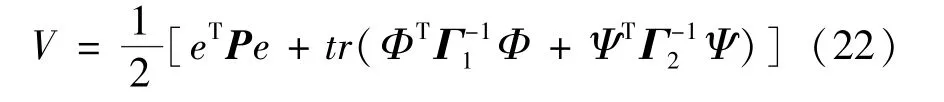
式中,P、Γ1和Γ2均为正定矩阵。

由于:

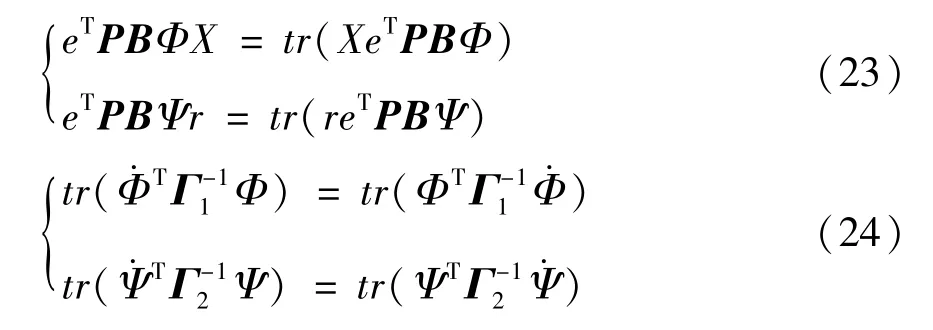
则由式(22)可得:

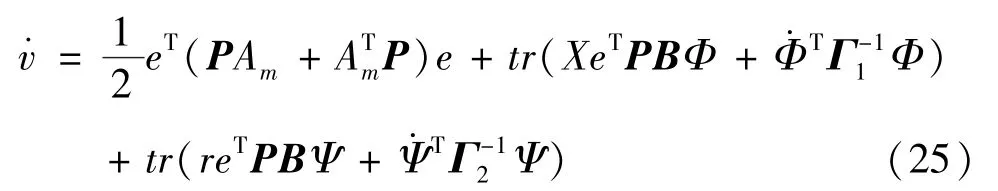
因为Am为稳定矩阵,为了可以选定对称矩阵Q使得对任意e成立,式(25)右侧第2 项和第3 项必须恒为零,因此选

当A和B为常值或变化缓慢时:

由此可得:

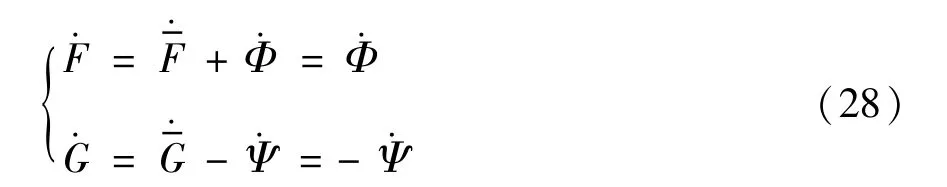
由式(26)～式(28)可得,前馈增益G和反馈增益F的自适应律为

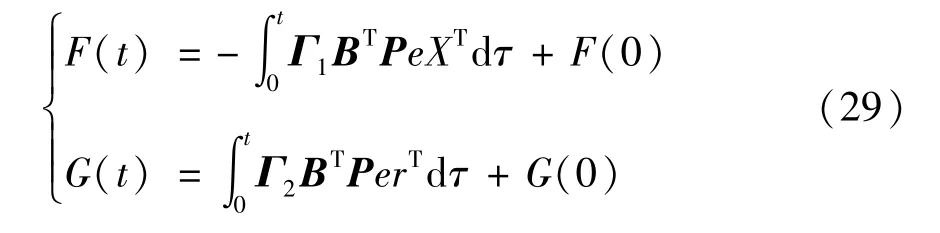
式(29)确定的自适应律就可以保证李雅普诺夫函数V正定和负定,此时对于任意分段连续输入向量函数r都能够保证模型参考自适应控制系统是全局渐进稳定的,即limt→∞e(t)=0。

3 仿真与实测实验

将表1 中的数值代入式(15)中,可得球形机器人系统的动力学模型参数为

选取球形机器人系统的期望极点为-10,-10,,则其参考模型参数为,Bm=B。

由式(22)可知,式(29)中P、Γ1和Γ2均为正定矩阵。在实际应用中,一般Γ1和Γ2取单位矩阵,P矩阵需要根据广义误差状态方程取合适的矩阵,本文经过反复仿真实验,当对称矩阵,此时广义误差收敛效果最好,其响应曲线图如图4所示,图中e1、e2、e3和e4为广义误差向量e的4 个状态分量。

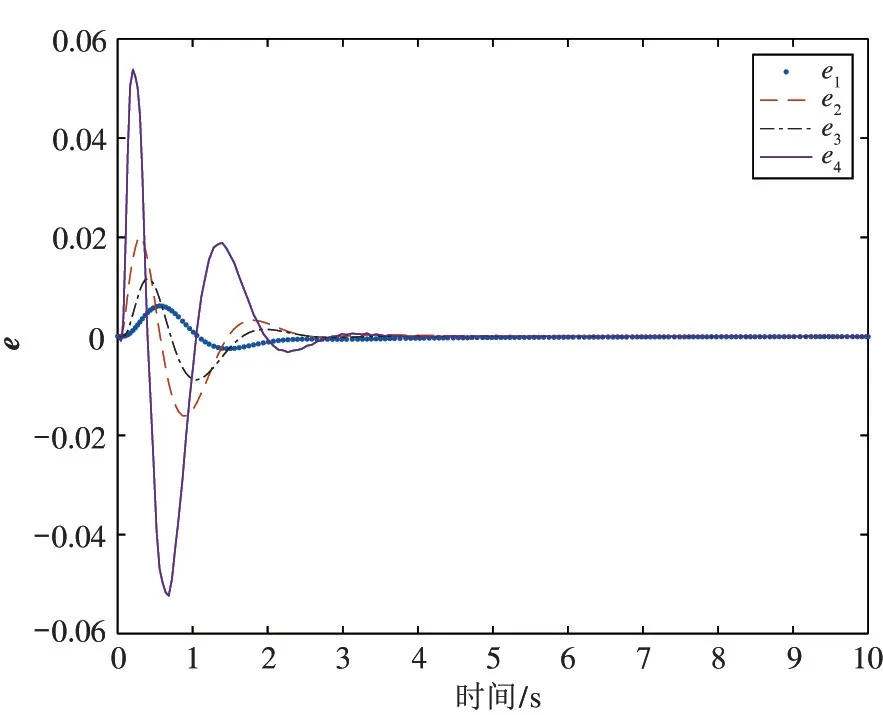
图4 广义误差

为验证控制器性能,将本文所设计的基于MRAC 的球形机器人控制系统与基于状态反馈控制的球形机器人控制系统进行对比。其中,状态反馈控制器的期望极点与MRAC 控制器中参考模型期望极点相同。

3.1 控制性能验证

图5 和图6 分别为球形机器人在阶跃响应下球心位置x和驱动平台摆角θ的变化曲线。

由图5 和图6 可知,本文算法与状态反馈控制输出基本相同,都能够在3 s 左右快速达到指定位置并稳定下来。由于状态反馈控制的期望极点与MRAC 控制器中参考模型期望极点相同,且在MRAC 控制器中,系统输出是利用参考模型与系统模型输出之间的误差,调节反馈增益和前馈增益,使系统模型能够跟随参考模型,因此该实验结果表明本文搭建的模型参考自适应控制系统中系统模型输出能够很好地跟踪参考模型输出,具有较好的控制效果。

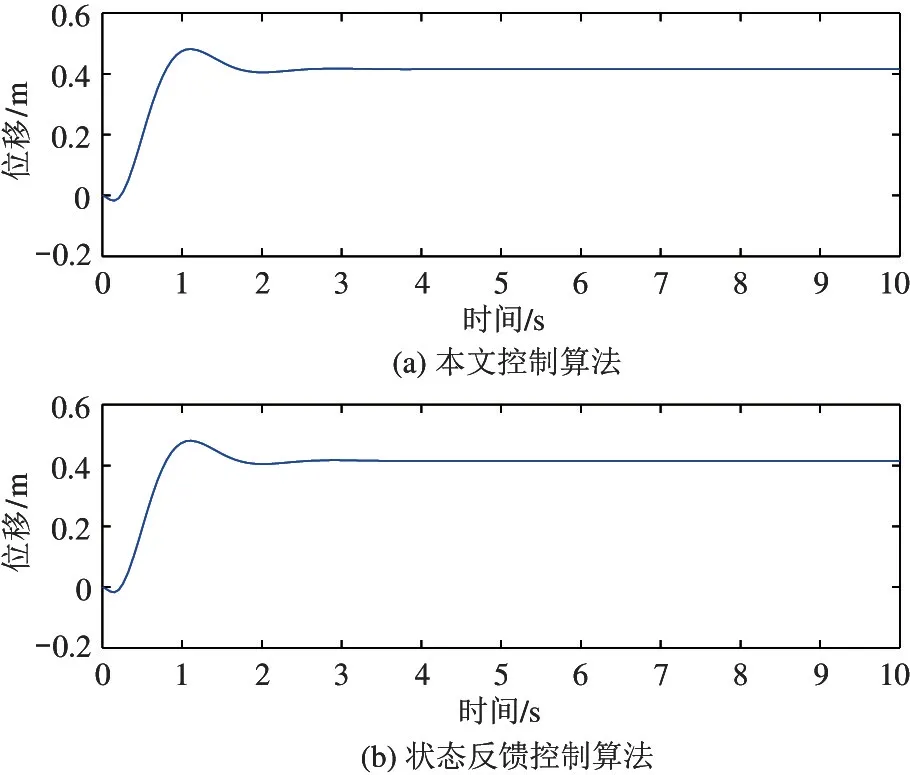
图5 球心位移变化

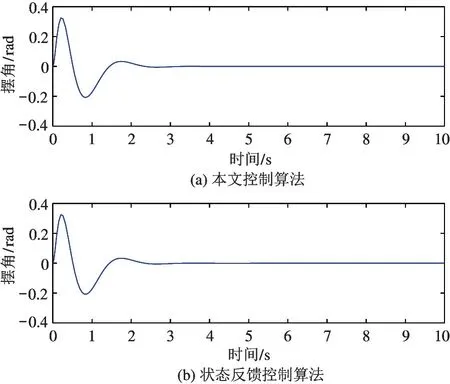
图6 驱动平台摆角变化

同时,通过球形机器人球心位移曲线和驱动平台摆角曲线可知,在球形机器人运动过程中,驱动平台首先快速向前运动到最大摆角位置,使球形机器人重心前移,并开始加速向前运动;当即将到达给定位置时,驱动平台摆角开始反向增大,使球形机器人开始减速,最终,通过内部驱动平台的几次调整,球形机器人速度为0,并达到给定位置。这与球形机器人实际运动情况相符合,也说明了本文建立的动力学模型的正确性。

3.2 抗扰动验证

为测试系统的抗扰动能力,本文在仿真中第3 s时加入冲激信号。图7 和图8 分别为在有扰动情况下球心位置x和驱动平台摆角θ的变化曲线。

由图7 和图8 可知,当在第3 s 产生扰动时,虽然内部驱动平台开始出现一定程度的摆动,但球形机器人几乎没有产生位移,并在经过大约2 s 后,球形机器人系统就能够完全恢复稳定。由此可以得出,模型参考自适应算法在扰动作用下也能够快速跟踪参考模型,有效对抗扰动,在短时间内就能恢复系统稳定,具有与状态反馈控制器相当的抗干扰能力。

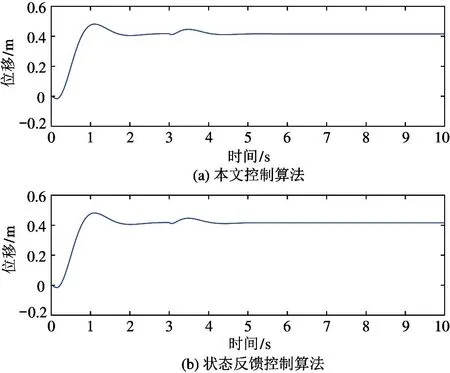
图7 球心位移抗扰动实验

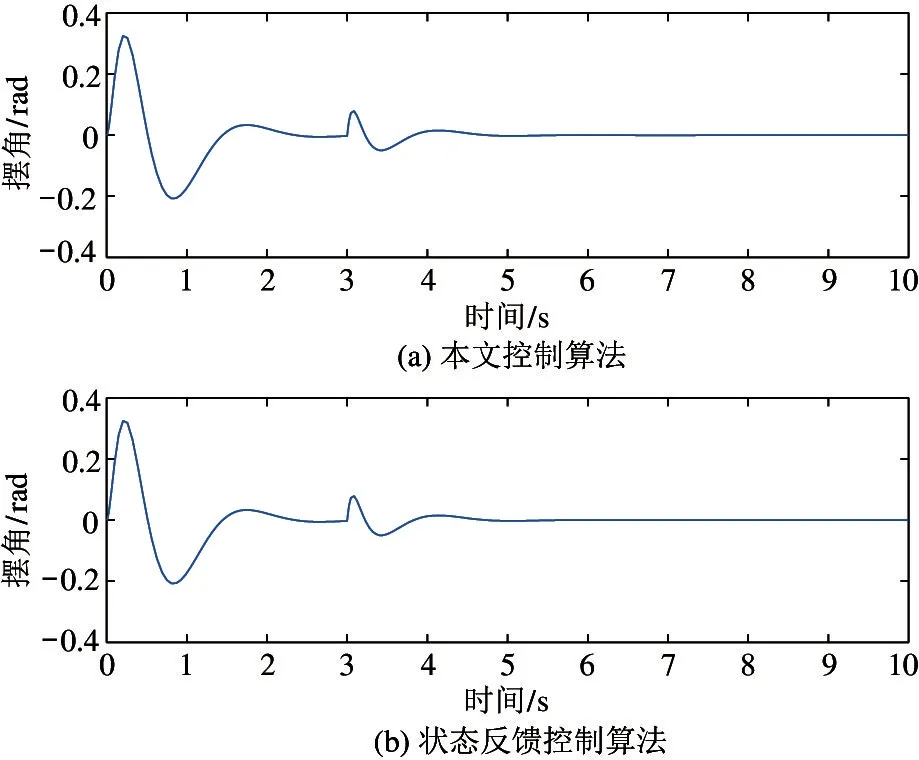
图8 驱动平台摆角抗扰动实验

3.3 鲁棒性验证

考虑到在球形机器人运动过程中,系统参数可能产生变化,为模拟系统参数发生20%的变化情况,本文将表1 中各参数数值扩大1.2 倍,控制器参数和结构不变。图9 和图10 分别为参数不确定情况下使用本文算法和状态反馈控制方法,球心位移和驱动平台摆角变化情况。

由图9 和图10 可以看出,当系统受到一定程度的不确定参数的影响时,模型参考自适应控制算法仍然能够具有较好的控制效果,球心位移和内部驱动平台摆角虽然相对于参考模型产生了一定的误差,但是仍然能够大致跟踪参考模型的输出,并且能够在3 s 左右恢复稳定,并收敛至与参考模型相同的位置。但是状态反馈控制在参数发生20%的变化时已经开始产生震荡,系统的稳定性大大降低。因此,实验结果可以证明本文所设计的MRAC 控制器对于系统参数不确定性具有很强的鲁棒性。

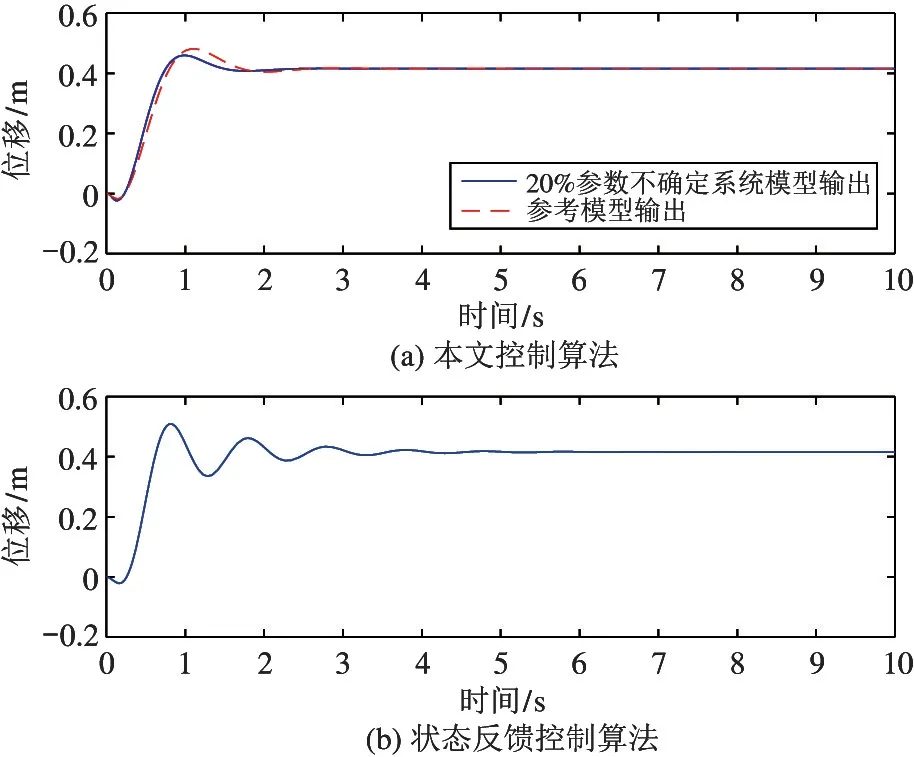
图9 参数不确定下球心位移

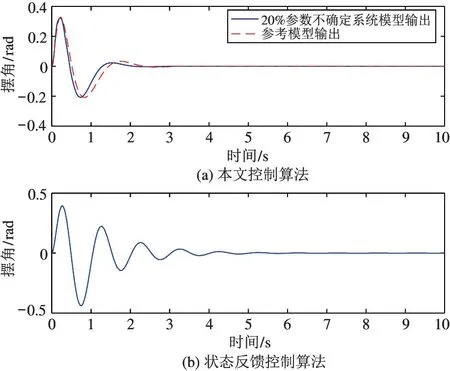
图10 参数不确定下驱动平台摆角

3.4 实际运行验证

基于图1 所搭建的球形机器人,本文分别进行了直线轨迹跟踪运动和圆形轨迹跟踪运动实验,并通过离线方式将运动曲线记录下来,验证所设计MRAC 的球形机器人控制系统的运行效果。

图11 和图12 为球形机器人直线运动实验,直线轨迹长度为240 cm,球形机器人运行时间为6 s。球形机器人的直线轨迹跟踪结果如图11 所示,图中实线为预期轨迹、虚线为球形机器人的实际运动轨迹。图12 为4 个不同时刻球形机器人的位置。由图11和图12 可以看出,在球形机器人启动时,虽然由于滑动摩擦以及自身惯性等影响产生了较小偏差,但是能够较快调节到期望位置,在整个运动过程中,球形机器人能够较为精确地按照预定轨迹滚动。

图11 直线运动轨迹

图12 不同时刻球体位置

图13 为球形机器人在圆周运行轨迹,图14 是在圆周运动中不同时刻相应位置。图中,圆环半径为75 cm,实线为预期轨迹、虚线为球形机器人的实际运动轨迹,球形机器人整体运行时间为30 s。在圆形轨迹运动过程中,由于轨迹较为复杂,内部全向轮与球壳之间存在滑动摩擦,因此在运动过程中出现了一定偏差,但是总体仍能够按照预定轨迹运行。因此,根据实验可知,模型参考自适应控制算法能够有效地应用于球形机器人实际系统中。

图13 圆形运动轨迹

图14 圆周运动不同时刻位置

4 结论

本文针对全向轮驱动的球形机器人系统,建立了其拉格朗日动力学模型,并利用模型参考自适应控制算法,设计了运动控制系统。实验表明,本文所采用的模型参考自适应控制能够有效应用于球形机器人控制系统,在有干扰的情况下能够快速恢复稳定,特别在球形机器人系统参数不确定的情况下,模型参考自适应控制算法仍然能够很好地对球形机器人进行控制,达到了预期的效果。