信源数量估计的可视化线性聚类方法①

何选森 何 帆 孟凡臣 徐 丽

(*广州商学院信息技术与工程学院 广州511363)

(**湖南大学信息科学与工程学院 长沙410082)

(***北京理工大学管理与经济学院 北京100081)

0 引言

在信号处理中,充分利用信源本身具有的稀疏性对数据分析具有重要的作用[1-2]。然而,在实际的工程中,信源一般是无法直接获得的,而是要通过传感器采集来得到相应的观测数据,采集的过程就相当于通信系统的传输信道[3]。当信源充分稀疏时,观测数据呈现出明显的线性聚类特性[4]。根据观测数据点形成的直线数量可以得到不可观测的信源的数量[5],而直线的方向则反映出信道所具有的特性[4]。因此,稀疏表示[6-7]和联合稀疏表示[8-9]就成为对信号模拟的有效工具。对于稀疏信号,聚类分析[10-11]已经成为信号处理和数据分析的基本方法。另外,在音频、图像信号处理和观测数据分析中,估计信源(聚类)的数量[12-13]具有十分重要的作用,准确估计信源数量是盲信号处理与数据分析的基础。

在信号处理和数据分析中,首要的任务是对信号进行表示[14]。最简单、最直接的表示方法是采用线性变换法。设时域中的信源向量s(t) ∈Rm为m维,观测数据向量x(t) ∈Rn为n维,对应的变换矩阵为A∈Rn×m。当m=n,即信源向量与观测数据向量的维数相同时,矩阵A是一个方阵,其变换称为正交变换。在实际应用中,由于信源是未知的,采集所用的传感器数量一般是与信源数量是不相同的,即m≠n。考虑到采集设备的成本,实际上希望传感器的数量应尽可能得少,即n ＜m。在这种情况下,矩阵A对应于超完备变换,而在稀疏表示中,把该矩阵A称为超完备字典[15-16]。所谓的稀疏表示就是在超完备字典中用少量的基向量来表示观测数据[7]。

在对稀疏信号的聚类分析中,K-均值算法[17]起着非常重要的作用,因而成为经典的聚类算法。然而,K-均值需要事先知道聚类(信源)的数量[18],这就限制了它的应用。为此,通过对观测数据的聚类分析,估计出信源的数量将扩展K-均值算法的应用范围。另外,信号在时域中的稀疏性表现得并不理想,通常是把时域信号转换到变换域中以增强信号的稀疏性[3]并进行聚类分析。例如,音频信号的稀疏特性和聚类特性在频域中能得到充分地体现。

正是基于这种考虑,本文提出一种在频域中估计信源数量的可视化聚类分析方法。利用信号频谱实部与虚部之间夹角的阈值,构造单源点(singlesource-point,SSP)检测技术,去除观测数据中的多源点和离群点(野值),以突出稀疏信源本身所具有的线性聚类特性,使得观测数据点聚类形成明确的直线。用直线的数量直观地估计信源的数量,而直线的方向向量则表示信道矩阵。

1 信号的稀疏表示

设时域中的信源向量为s(t)=[s1(t),s2(t),…,sm(t)]T,观测数据向量为x(t)=[x1(t),x2(t),…,xn(t)]T,从信源到观测数据的变换矩阵为A∈Rn×m,则观测数据表示为线性瞬时模型

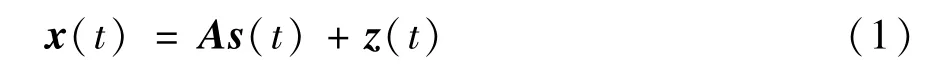
其中z(t)=[z1(t),z2(t),…,zn(t)]T为噪声向量。在获取观测数据的过程中,如果不考虑其他的外界环境干扰噪声,仅考虑采集信道的特性,可以把时域中观测数据的线性模型简化为

矩阵A体现了信道的全部特性。在通信系统中,信道一般为加性高斯白噪声(additive white Gaussian noise,AWGN)信道。将时域中观测数据模型式(2)表示为矩阵形式

其中,矩阵A中的元素{aij,i=1,2,…,n,j=1,2,…,m} 为常数。为了便于对数据进行分析,把信道矩阵A分解成它的列向量

其中向量ai=[a1i,a2i,…,ani]T(i=1,2,…,m)。于是,观测数据为

稀疏信号是指它的绝大多数样本点的幅度为零值或非常接近于零值,而仅有少量样本点的幅度远离零值(即非零值)[4-5]。若信源向量中所有信号都是充分稀疏的,则在任一个时域样本点t,仅仅只有一个信源si(t) 是非零的,其余的信源均为零值[5]。在满足充分稀疏条件下,观测数据的表示式(5) 就具有更简洁的形式

显然,式(7) 的几何意义是通过原点的一条直线。该直线的方向向量ai=[a1i,a2i,…,ani]T就是信道矩阵A的第i个列向量,即每个信源确定出一条这样的直线,这就是稀疏信号的线性聚类特性。通过对观测数据x(t)的线性聚类分析就可以估计出信源s(t)的数量。

为了使信号的稀疏特性得到充分体现,把时域的观测数据x(t)转变成频域中的频谱X(k),其中k为离散频率点。对于音频信号,常用的变换为快速傅里叶变换(fast Fourier transform,FFT)和短时傅里叶变换(short time Fourier transform,STFT)等。实际上STFT 就是有限时间长度的FFT,本文采用STFT。对时域观测数据的模型式(2),在等式两边分别取STFT,得到频域表示式为

其中X(k)=[X1(k),X2(k),…,Xn(k)]T和S(k)=[S1(k),S2(k),…,Sm(k)]T分别为x(t) 和s(t)在频率点k的STFT 系数(频谱)。

当信号充分稀疏时,频域中的数据点将在平面(或空间) 上聚类形成若干条经过原点的直线。然而,在实际应用中,信号在频域中仍表现为具有一定的稀疏性,而并非是充分的稀疏[2]。在一些频率点上可能会有2 个或2 个以上的信源同时都具有不可忽略的能量(非零的幅度),导致在这些频率点上的观测数据不再聚类在一条直线上,而是在直线旁边还分布很多干扰的数据点。这就造成观测数据的线性聚类特性下降,使估计信源数量变得困难。因此,需要对观测数据进一步处理以凸显稀疏信源的线性聚类特性。

2 单源点检测

由式(6) 和式(7) 可以看出,对于充分稀疏的信号,在某个频率点上,信源向量中仅有一个分量的幅值为非零,而其他分量的幅值都为零,这样的频率点就称为单源点(SSP)[19-20]。换句话说,所谓的单源点是指这样的频率点,在该频点上只有一个主导信源的能量具有较大的幅值,而其余信源的能量很小以至可被忽略。

对于式(8) 给出的频域观测信号X(k),假设在某个频率点k0上只有一个信源Si(k0) (i=1,2,…,m) 具有较大的能量值,而其余的信源Sj(k0) (j≠i)的能量均为零值,则该频率点k0为单源点(SSP),即

对于不满足SSP 条件的频率点,则称为多源点(multi source points,MSP)。造成稀疏信源线性聚类特性下降的原因,就是在观测数据中存在这些多源点。因此,为了凸显信号的线性聚类特性,需要去除MSP 而仅保留SSP,这就是单源点检测[20]。

频域中观测信号的频谱X(k) 是复数,它可以用极坐标形式表示为幅度与相位,也可以用直角坐标形似表示为实部和虚部。

对单源点的式(9) 两边取相位角(设i=1,即在频率点k0处,只有信源S1具有非零幅度值,其他信源均为零幅度值),可得

这表明,观测信号X(k0) 中每一个分量的相位角与信源S1(k0) 的相位角是一致的。同样地,把式(10)用实部和虚部表示为

即观测数据X(k0)中每一个分量的虚部与实部的比值与信源S1(k0) 的相应比值是一样的。这就是单源点的频谱所具有的特性。

如果在某个频率点k1处,有2 个信源S1(k1) 和S2(k1) 具有非零的幅度值,其余信源为零幅度值,则由式(8) 可知

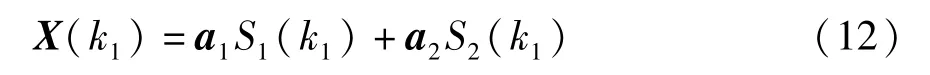
对式(12) 两边分别取实部分量和虚部分量,则有

因此可得X(k1) 的相位角为

如果观测数据X(k1)的每一个分量的相位角是相同的,即每个分量的实部与虚部的比值是相同的,则向量a1和a2的关系为

这表明,只有当向量a1和a2具有严格的比例关系,观测数据X(k1) 的每个分量的相位角才是相同的,即其实部与虚部的方向相同。根据稀疏信号的线性聚类特性,观测数据方向的列向量依赖于信道矩阵A的列向量。因此,在1≤i,j≤m并且当i≠j时,要求I[Xi(k)]/R[Xi(k)]=I[Xj(k)]/R[Xj(k)],这样才能确定单源点。然而,在实际中由于测量误差的存在使得式(16) 是很难满足的。于是,考虑到实际的应用环境,可采用一个误差参数ε∈(0,1) 来放松限制条件,即

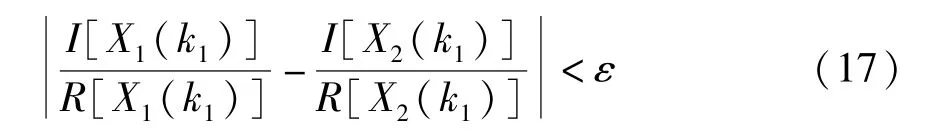
满足这些条件的频率点k1也称为单源点(SSP)。

推广到一般情况,对于任意频率点k,由n个传感器采集m个信源的频域模型,由式(8) 可得观测数据的实部和虚部分量分别为

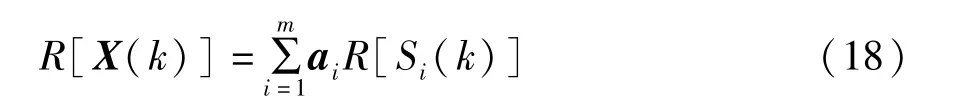
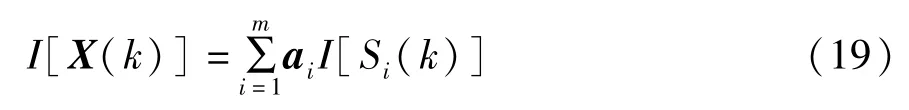
并定义实部分量与虚部分量之间的夹角[1]

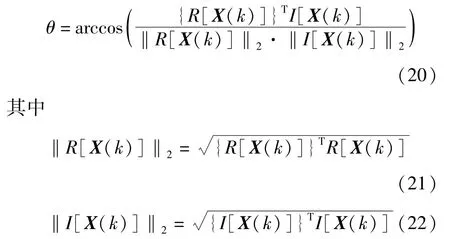
分别为频谱X(k) 的实部R[X(k)]与虚部I[X(k)]的l2范数[2]。当夹角θ=0 时,观测数据实部R[X(k)]与虚部I[X(k)]的方向是相同的,即

另外,当夹角θ=π(180°) 时,R[X(k)]与I[X(k)]的方向是相反的。综合以上2 种情况,当夹角为0 或π 时,统称R[X(k)]与I[X(k)]的绝对方向是相同的。满足该条件的频率点也称为单源点(SSP)。

然而,在实际应用中,由于误差和干扰的存在,利用观测数据频谱的实部与虚部分量的绝对方向相同(即θ=0 或θ=π)的条件来判断单源点是相当苛刻的。为此,将SSP 的判断条件进一步放宽为

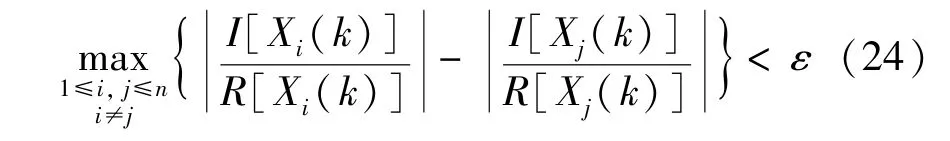
其中ε为误差容限,| g|表示g的绝对值。这是用不同观测数据频谱的虚部分量与实部分量的比值关系来判断单源点。

类似地,也可以通过指定一个夹角θ的门限值(阈值)Δθ,当观测数据频谱实部分量与虚部分量的夹角小于该门限,即

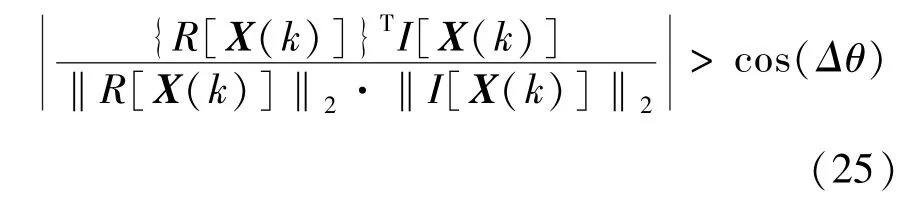
时,其对应的频率点为单源点。

式(24)和式(25)就是本文提出的单源点检测的条件,在实际应用中,采用式(25)更为方便。对于观测数据X(k)中不满足条件式(25)的多源点,直接予以删除;而仅保留满足条件式(25)的SSP 数据点,形成了经过SSP 检测后的观测数据集合Xssp。显然,数据Xssp的稀疏性得到了充分体现,Xssp的数据点在平面(或空间)上线性聚类产生的直线的数量与方向性变得更加清晰。因此,利用Xssp就可以从观测数据的聚类结果中直观地估计出信源的数量。在实际应用中,式(24)中的误差容限ε还需要根据信源类型来具体确定。

3 实验及结果分析

为了验证本文方法的有效性,利用3 个传感器对不同数量的音频信源进行采集,通过仿真实验分析线性聚类的结果。

实验的PC 机硬件配置为Intel(R) Celeron(R)1007U-1.5 GHz 的CPU,4 GB 内存,操作系统为Windows 10,所有的仿真实验都是在Matlab 9(R2016a)上运行。用于测试的信源为SixFlutes(长笛演奏音乐信号) 数据集[21],信号采样频率为44.1 kHz,信号样本长度为216=65 536。六路信源向量为s(t)=[s1(t),s2(t),s3(t),s4(t),s5(t),s6(t)]T。在时域中,信源的波形如图1 所示。

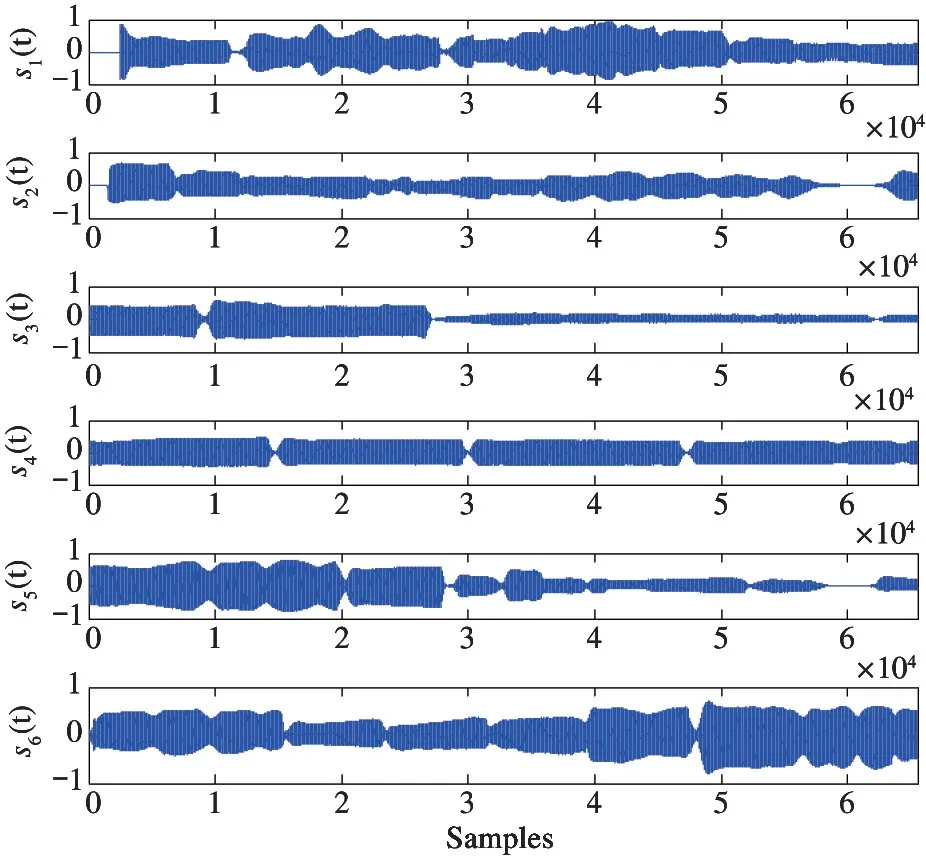
图1 六路音乐音频源信号的时域波形

在进行聚类分析时,数据的散点图是一种直观的表示方法。所谓散点图是指数据点在直角坐标系上的分布图,它表示了不同分量之间变化的大致趋势。对于稀疏信号,其散点图在平面或空间上形成数据点的直线,反映了数据的线性聚类特性。

3.1 三个传感器采集四路信源

四路信源为s(t)=[s1(t),s4(t),s5(t),s6(t)]T,利用3 个传感器对该信源进行采集,即变换(采集信道) 矩阵为A∈R3×4。信道矩阵服从白噪声分布,矩阵A是由Matlab 命令A=rand(3,4) 随机地生成。然后由x(t)=As(t)=[x1(t),x2(t),x3(t)]T形成时域的观测数据,这三路观测信号的数据点构成的时域三维散点图如图2 所示。

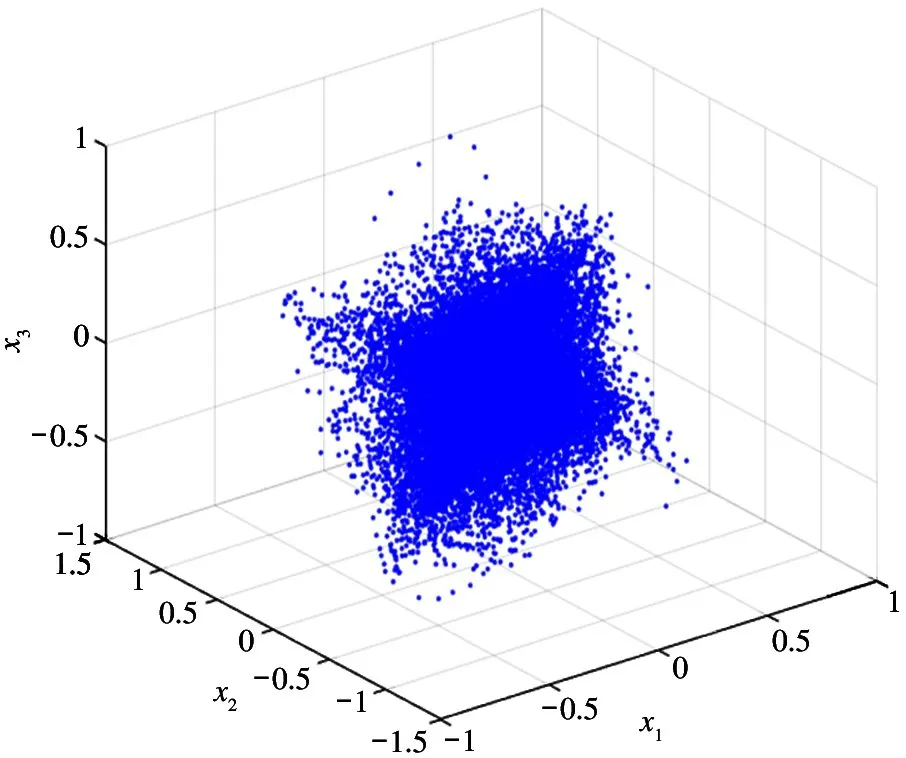
图2 四路信源生成三路观测数据的时域散点图

从图2 可以看出,时域中三路观测信号的数据点基本都集中在直角坐标的原点附近,越靠近原点其数据点越浓密。显然,数据的时域散点图没有呈现出信源的稀疏特性,无法进行聚类分析。

对时域的观测数据进行STFT,得到信号在频域的离散频谱X(k)=[X1(k),X2(k),X3(k)]T,其对应的频域散点图如图3 所示。

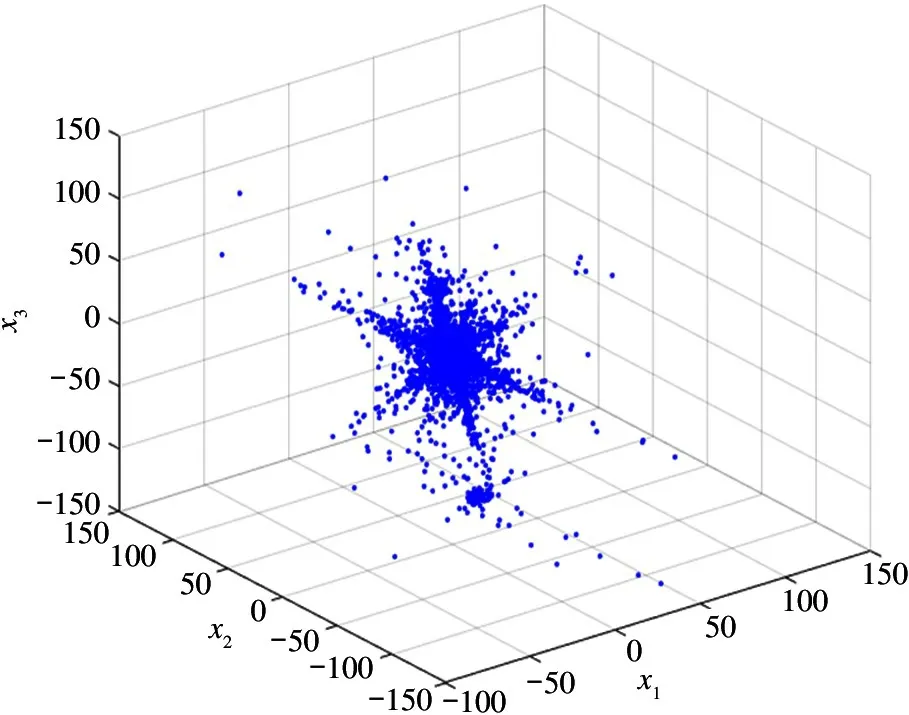
图3 四路信源生成三路观测数据的频域散点图

从图3 可看出,三路观测信号的数据点基本呈现出四路稀疏信源的线性聚类特性,但直线呈现的并不明显,因为在数据点形成的直线之间,仍然分布着许多数据点(MSP),造成线性聚类的直线数量和直线方向都不明确。换句话说,稀疏源的线性聚类特性在频域中并没有得到充分体现,还需要对观测数据进一步处理。

对频域数据X(k)执行SSP 检测,其中的角度阈值是根据信号的类型来选取的。对音频音乐信号,常用经验公式Δθ≈45.84×π/180 ≈0.8 ° 来计算。SSP 检测一方面把靠近直线的数据点聚类到对应的直线上,另一方面把远离直线的离群点作为MSP 删除,形成了经过SSP 检测的数据XSSP,其对应的散点图如图4 所示。

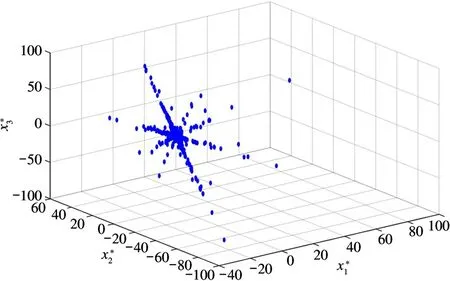
图4 SSP 检测后三路观测数据的散点图

从图4 可以看出,信号XSSP数据点的线性聚类特性得到了充分的体现,数据点在三维空间形成了明确的4 条直线。从散点图可直观地估计出信源的数目为4 个,且直线的方向也是确定的。

3.2 三个传感器采集六路信源

该仿真实验与上一个实验的过程基本相同。

采用3 个传感器对图1 所示的六路信源s(t)进行采集,信道矩阵由Matlab 命令A=rand(3,6) 随机地生成。由此获得的观测信号x(t)=As(t)=[x1(t),x2(t),x3(t)]T在时域中的散点图如图5所示。

图5 六路信源生成三路观测数据的时域散点图

从图5 可看出,x(t)在时域中的数据点形成了一个以坐标原点为中心的范围较大的接近于椭球形的数据点簇。由于数据点密集地重叠在一起,从图5 的散点图无法分辨出数据的属性,即哪些是单源点(或多源点)。这说明在时域中信源的稀疏特性没有得到体现,也就无法进行聚类分析。为此,利用STFT 把数据x(t)变换成频谱X(k)=[X1(k),X2(k),X3(k)]T。X(k)的频域散点图如图6 所示。

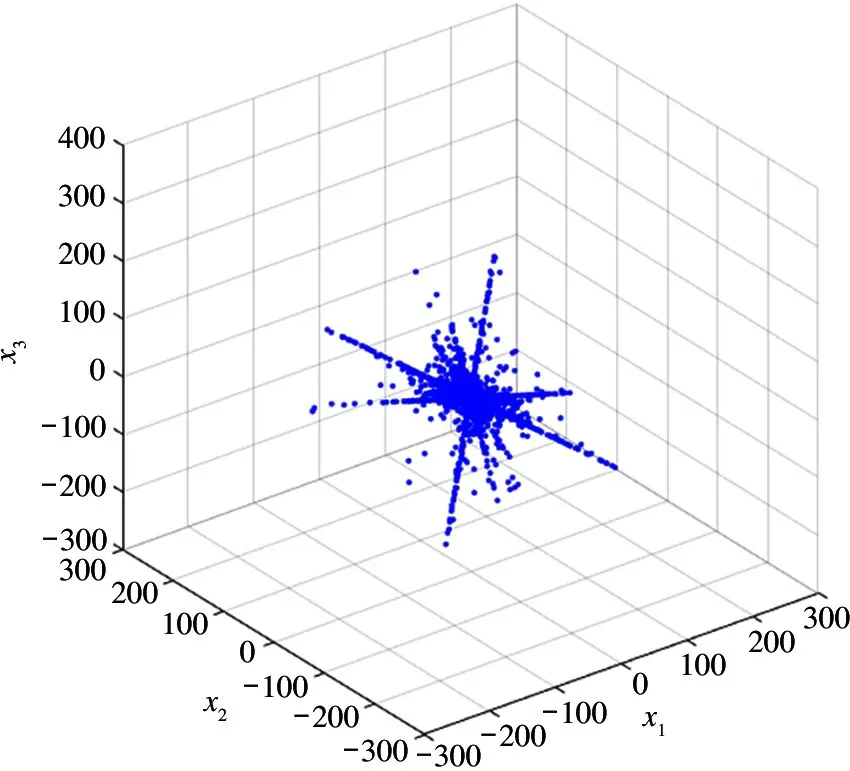
图6 六路信源生成三路观测数据的频域散点图

从图6 可知,在频域中信源的线性聚类特性得到一定体现,基本可观察出数据点形成的直线。尽管如此,在几条直线之间仍然分布着很多数据点(MSP),这些点干扰了稀疏源的线性聚类特性,使得直线的数量和方向都具有不确定性。

对频谱X(k)采用单源点检测,其中角度阈值仍取Δθ=0.8 °。经过SSP 检测后的数据XSSP的散点图如图7 所示。

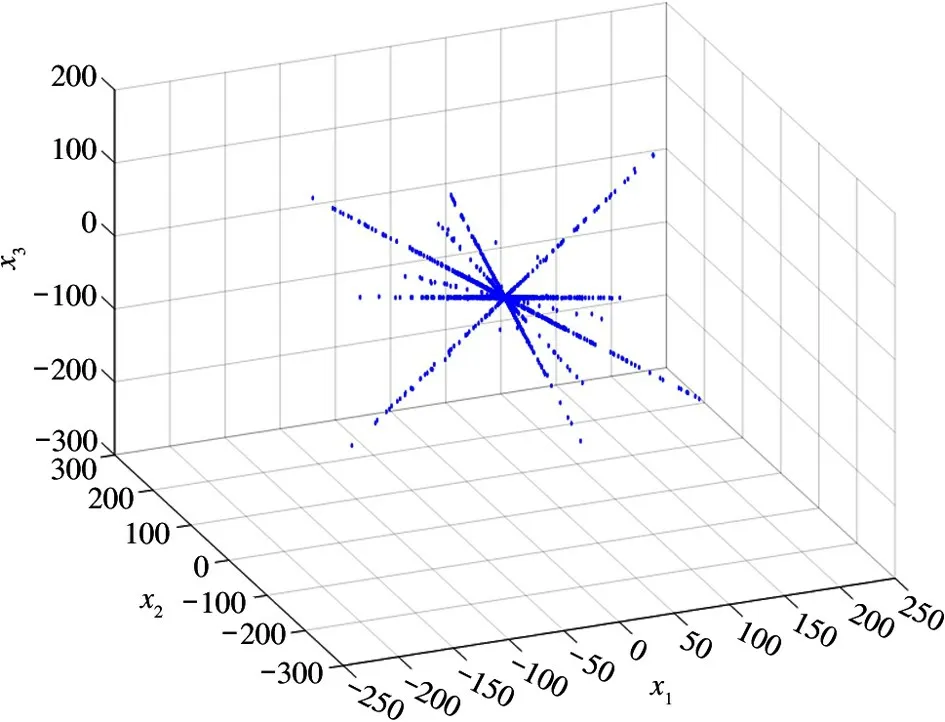
图7 SSP 检测后六路信源生成三路观测数据的散点图

从图7 可以看出,XSSP的数据点形成了明确的6条直线,即估计出信源数量为6 个,而且直线的方向也非常清晰。

从以上2 个仿真的实验结果可知,在时域中信号的稀疏性得不到体现。因此,聚类分析一般是在频域中进行的。将时域信号变换到频域中能够增强信源的稀疏性。然而,在频域中,稀疏信源的线性聚类特性只是在一定程度上得到反映,并没有得到充分的体现,即观测数据形成的直线数量和直线方向都不明确。为了直观地估计信源的数量,利用单源点检测可以使稀疏源的线性聚类特性得到充分的体现,使得观测数据通过线性聚类形成的直线数量和直线的方向都非常明确,以便于对数据做进一步的处理。

观察以上2 个经过SSP 检测的数据散点图可知,与图4 相比较,图7 中数据形成直线的方向性更加明确和清晰。这说明,随着信源数量的增加,采用单源点检测的线性聚类效果更为突出。

4 结论

实际应用中,信源一般是不可观察的隐变量,只能通过传感器采集而获得对应的观测数据。在信号处理与数据分析中,对信源数量的估计将具有非常重要的意义。本文致力于在变换域中对稀疏信源进行聚类分析。为了增强信源的稀疏性,采用单源点检测剔除观测数据中的多源点,以凸显信源的线性聚类特性。在考虑采集信道噪声的影响下,提出了一种频域中观测信号实部与虚部夹角的阈值,利用该阈值构成了单源点检测的条件。本文提出的增强稀疏信源线性聚类特性的方法,可作为解决欠定盲源分离问题的预处理技术,同时对于其他数据分析应用也具有重要的意义。