全海深ROV 非金属铠装脐带缆动力学性能研究①

王海龙 张奇峰 全伟才 崔雨晨* 闫兴亚

(*中国科学院沈阳自动化研究所机器人学国家重点实验室 沈阳110016)

(**中国科学院机器人与智能制造创新研究院 沈阳110169)

(***湖南科技大学海洋矿产资源探采装备与安全技术国家地方联合工程实验室 湘潭411201)

(****中国科学院大学 北京100049)

0 引言

遥控潜水器(remotely operated vehicle,ROV)是一种有缆遥控无人潜水器,通过脐带缆传输动力和信号,因其具有强大的水下作业能力,已成为海洋科学研究、海洋探查和资源开发等不可或缺的手段[1-3]。随着海洋装备研制能力和配套水平的提高,当前我国正在建设覆盖全海深的海洋探测作业体系,而全海深ROV 是该体系的重要组成部分[4]。

目前,制约全海深ROV 发展的首要瓶颈问题就是脐带缆,由于传统的ROV 采用金属铠装脐带缆,因受强度/重量比限制,其最大使用深度很难突破6000 m,更大深度的脐带缆的研制仍是一项国际技术难题。

世界海洋最深处是太平洋上的马里亚纳海沟,最深处达到11 034 m。由于受技术手段的限制,人类对该区域的研究甚少,目前仅日本和美国研制了相关无人潜水器开展了少量科学研究。其中,日本研制的最大工作深度11 000 m“海沟”号ROV 是国际上首套也是唯一一套全海深ROV。该ROV 系统采用中继器模式,母船与中继器之间通过主缆连接,中继器与ROV 之间通过次缆连接。而且仅有日本藤仓株式会社生产的非金属铠装脐带缆最大工作深度可达11 000 m,并成功应用于日本海洋科技中心研制的“海沟”号ROV。遗憾的是,2003 年6 月29日,“海沟”号ROV 在太平洋海域海底调查作业时由于次缆断裂导致丢失[5-8]。

根据我国深海科学技术发展战略规划,在国家重点研发计划支持下,中天科技海缆有限公司联合上海交通大学和沈阳自动化研究所等共同开展全海深ROV 非金属铠装脐带缆关键技术研究和试验,研制全海深ROV 非金属铠装脐带缆试验样品,完成光学、电气、动态力学、动力及信号传输等分析和试验,填补全海深ROV 非金属铠装脐带缆设计、制造、分析和测试技术空白。

目前,针对水下系泊系统、拖曳系统和ROV 铠缆系统等水下缆索动力学建模主要有3 种方法,即有限差分法、高阶有限元法和集中质量法。集中质量法忽略了节点间弯曲和扭转,仅考虑弹性因素的影响,属于低阶有限元法;有限差分法不适合处理低张力缆索问题,因为该算法在零张力时会出现数值奇点;高阶有限元法具有完整的物理意义和理论基础,能够很好地模拟缆索低张力动态特性[9-11]。

为了全面评估全海深ROV 非金属铠装脐带缆动力学性能,提高脐带缆在全海深ROV 系统应用的安全性和可靠性,本文针对不同海况,结合母船升沉运动状态,建立全海深ROV 非金属铠装脐带缆三维非线性动态力学模型,并对其在全海深应用环境下的扭转特性、在位运动等动态力学特性进行分析和研究,为全海深非金属铠装脐带缆的研制和安全使用提供理论支撑。

1 全海深脐带缆结构组成

根据全海深ROV 系统的设计需求,动力单元和控制单元供电相对独立,同时参照日本“海沟”号主缆结构形式,全海深脐带缆总体结构采用3 芯动力单元和2 芯控制单元共计5 芯结构,动力单元工作交流电压4160 V,末端输出功率不小于45 kW;控制单元工作交流电压3000 V,末端输出功率3～5 kW,结构示意图如图1 所示。脐带缆外径42 mm,空气中重量1.6 kg/m,水中重量0.5 kg/m,最小断裂强度400 kN,安全工作载荷66 kN,最小弯曲半径700 mm,最大使用水深11 000 m。

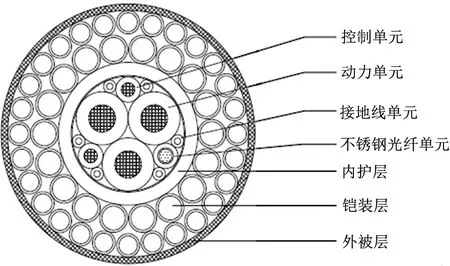
图1 全海深ROV 非金属铠装脐带缆结构示意图

2 脐带缆动力学建模

2.1 脐带缆动力学建模

为了分析方便,定义如图2 所示的运动坐标系,假设全海深ROV 非金属铠装脐带缆是连续的,初始形状直线,且截面圆形对称。其中,{Ei} 为惯性坐标系,在空间固定不动,空间坐标设为{E1,E2,E3}。{ei} 为材料坐标系,材料坐标设为{e1,e2,e3},其中e1与脐带缆初始中轴线相切,e2和e3位于脐带缆的初始横截面,为了分析方便,这里设ei≡Ei(i=1,2,3)。{ti} 则为运动坐标系,初始时刻与材料坐标系{ei} 重合。缆在初始状态的域称为初始构型,通常作为参考构型,变化后的构型称为当前构型。

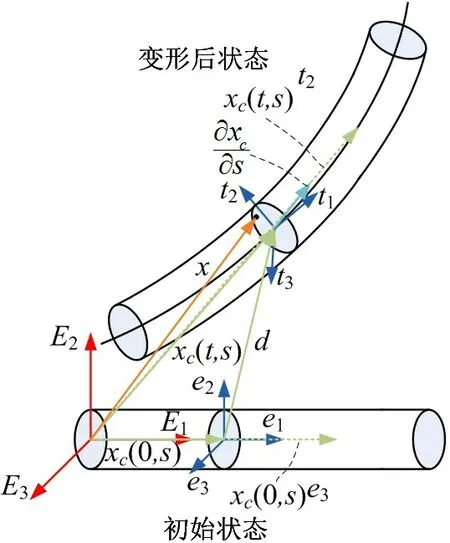
图2 全海深ROV 非金属铠装脐带缆运动坐标系

以上三坐标系基矢量间满足如下关系:

式中,t代表时间,s为参考弧长,ℜ0与ℜ 是正交张量算子,满足ℜℜT=I。其中ℜ0为初始转动张量算子,表征从固定空间坐标系{ei} 到材料坐标系{Ei} 的转换关系;ℜ 为当前转动张量算子,表征从材料坐标系{Ei} 到运动坐标系{ti} 的转换关系。

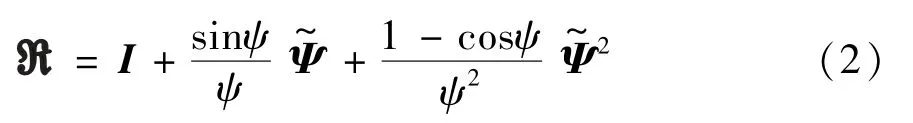
式中ψ=‖Ψ‖,即是脐带缆截面总转动矢量Ψ的长度,为矢量Ψ对应的反对称张量。脐带缆内任意材料点的运动学关系为

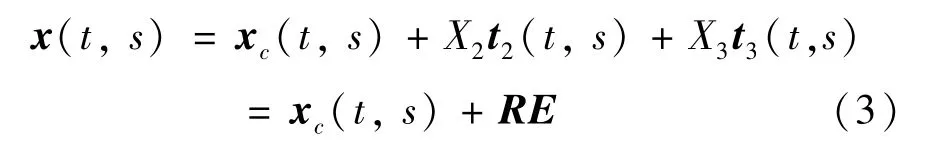
式中,E=X2E2+X3E3,xc(t,s) 是空间坐标系下的脐带缆中轴线位置矢量,其对应的空间虚位移为

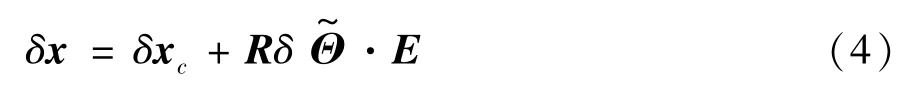
式中Θ称为转动矢量增量。对式(3)求二阶导数,可得:

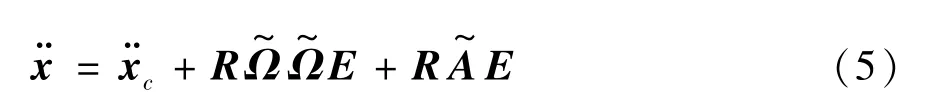
其中,,Ω为材料角速度矢量,A为材料角加速度矢量。

将Reissner-Timoshenko 运动学关系代入连续介质力学的线动量与角动量方程,应用分析力学范畴的虚功原理,得到脐带缆的非线性连续运动方程的等效弱形式,为后续的有限元模型的建立提供基础条件[12-13]。虚功原理可表述为

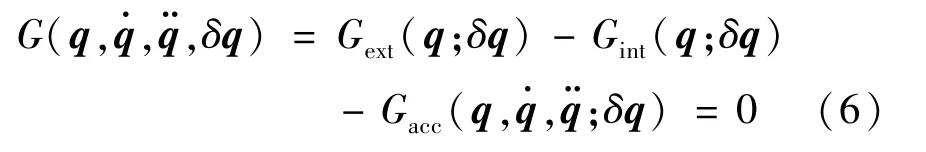
式中,q=(d,ψ) 为广义位置,Gext为外力作用虚功项,Gint为内力作用虚功项,Gacc为惯性力作用虚功项。

2.2 弱形式的完全拉格朗日列式

全海深ROV 非金属铠装脐带缆动力学方程的弱形式为高度非线性方程,很难得出直接的数学解析解,通常采用迭代校正的方法,来逐步逼近真实解,因此必须对完全拉格朗日列式进行线性化。通过对式(6)求导,可得整个虚功项的线性部分:

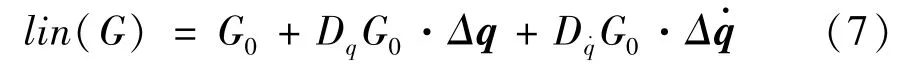
式中,下标0 表示在t=t0时刻的状态量,等号右边第1 项为给定状态下的残值,等号右边第2、3 项为相对于给定状态的线性增量。

2.3 完全拉格朗日列式的线性化

本节对弱形式的线性化表述采用有限单元进行离散,采用ne=2 节点线性插值等参单元,对广义位移矢量进行离散,得到:

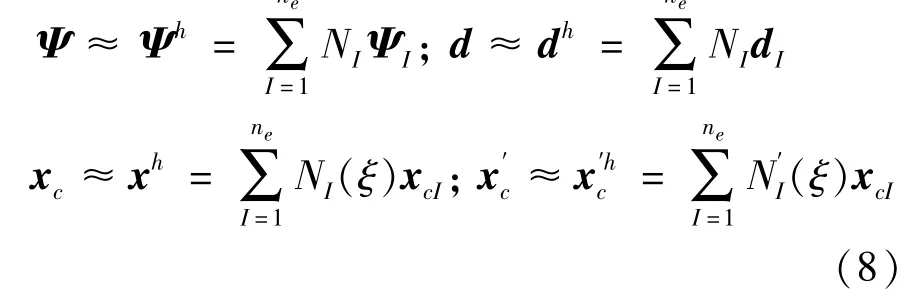
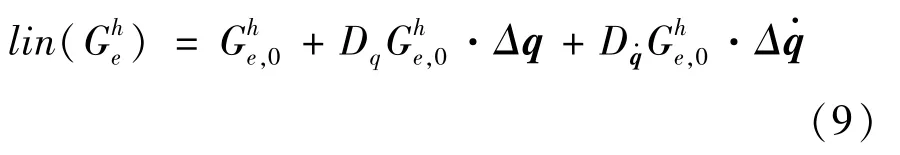
由式(7)可得对应的单元有限元方程为

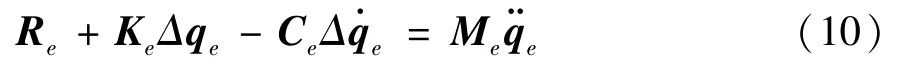
进而由单元有限元方程进行组装,方法与线性有限元中的组装方法是一样的,组装后得到的总体有限元方程,也即运动方程,记为

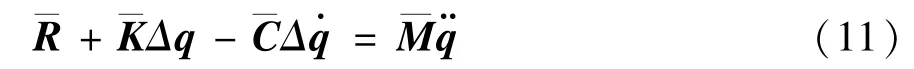
3 全海深脐带缆动力学性能分析

ROV 的作业环境较为复杂,影响其安全使用的因素较多,特别是恶劣海况下,脐带缆内部会出现高低张力波动的情况,可能达到缆索的破断强度,从而导致其断裂。ROV 在布放过程中,铠缆刚度也会随着ROV 下潜深度的增加逐渐降低,当脐带缆的固有频率逐渐进入母船升沉频率范围之内,将引发共振,影响ROV 收放的安全。

影响水下脐带缆安全工作的因素较多,主要包括:(1)支持母船的升沉运动;(2)铠缆自身参数变化;(3)海流流速变化等。由于各影响因素之间存在相互耦合,综合分析将很难发现影响规律,因此本文对单个因素影响规律进行研究,在此基础上,开展多因素耦合影响。

3.1 全海深脐带缆系统参数描述

全海深脐带缆截面材料基矢量E1、E2与惯性主轴平行,根据材料力学知识可得[14-16]:

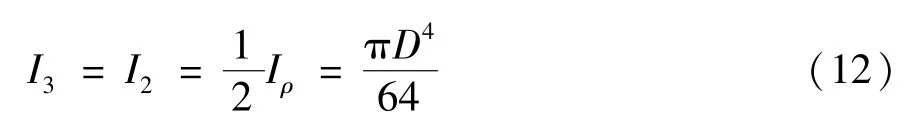
式中,I1、I2为截面的惯性矩,Iρ为极惯性矩。

假设全海深脐带缆模型截面各向是同性的,则弹性模量与剪切模量之间的关系为

其中,泊松比μ=0.1,其为脐带缆横向变形的弹性常数;将剪切模量G结合截面面积A与截面惯性矩Iρ就可分别得到剪切刚度GA与扭转强度GIρ。脐带缆界面的惯性张量分量可表示为

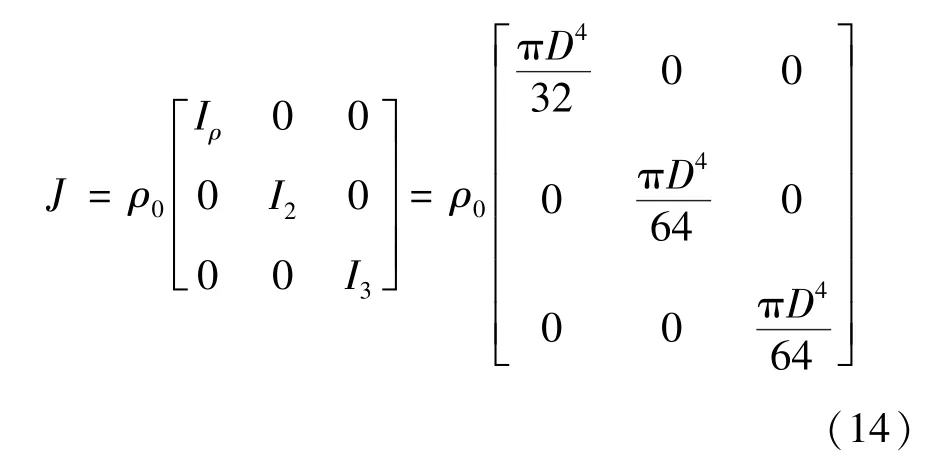
式中,参数D表示脐带缆截面直径。

若假设脐带缆材料模型是线弹性关系,则弹性张力用分量形式表示的矩阵为

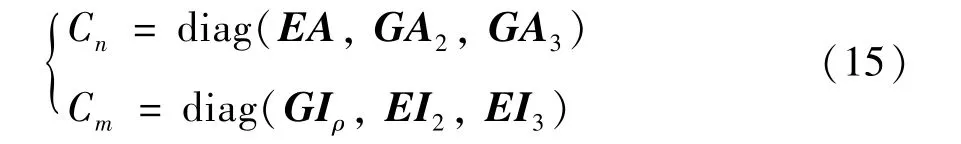
式中截面面积关系为

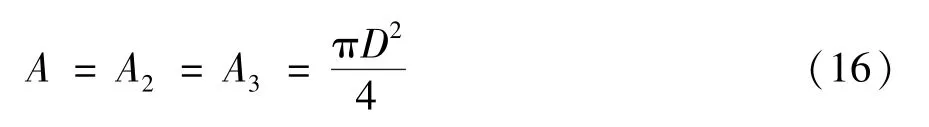
由式(12)～式(15),全海深ROV 非金属铠装脐带缆系统主要参数如表1 所示。

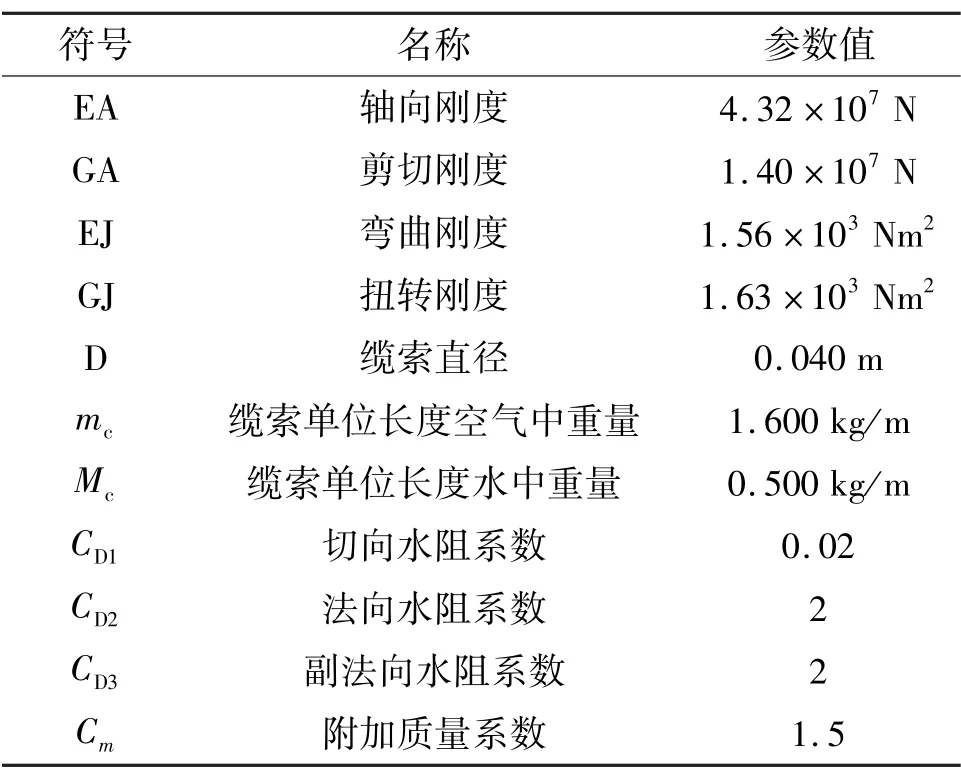
表1 全海深脐带缆主要机械性能参数

3.2 脐带缆动力学建模方法验证

为了验证所建立脐带缆动力学模型的正确性,结合加拿大深海ROV 系统ROPOS 进行实测数据验证。ROPOS 是带有中继器的ROV 系统,最大潜深5000 m,空气中重26 700 N,尺寸为2.6 m ×1.45 m×1.7 m。连接中继器与ROV 的是一段长约300 m的系缆,ROV 在回收时可以停靠在笼式中继器内。

以实测母船运动位移、速度和加速度数据为输入,计算脐带缆末端的中继器的位移、速度和加速度,并与实测的中继器运动数据进行对比,以此验证本文所建立的脐带缆模型、相应的算法和自编有限元程序的正确性。由图3 可知,计算值与实测值在100 s 内的时段内有相当好的吻合,初步验证了所建立脐带缆动力学模型的正确性。

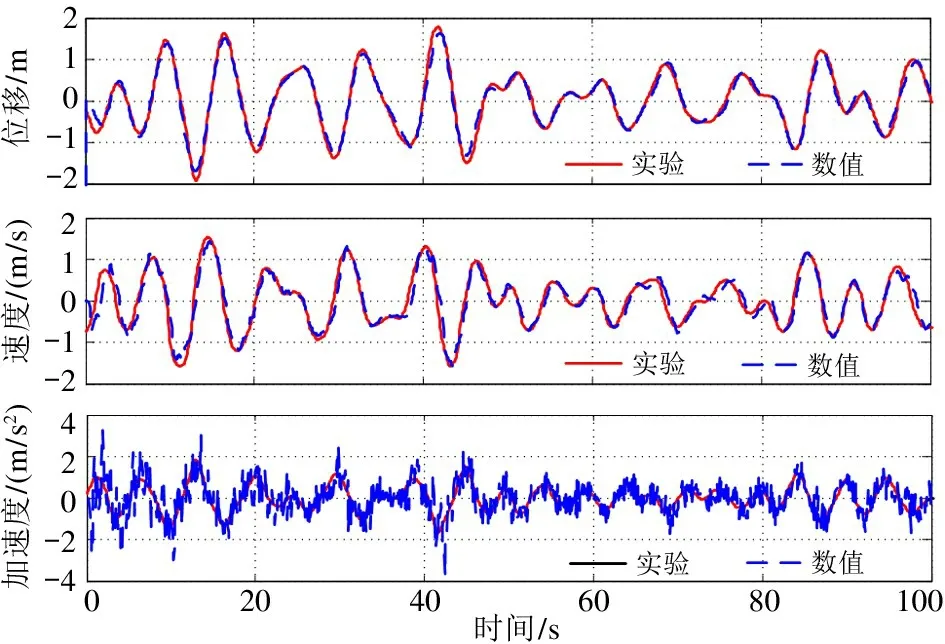
图3 有限元程序计算结果与实测数据的对比曲线

3.3 无母船升沉和无海流时的静态分析

为了获得全海深脐带缆系统动态力学性能分析的初始值,有必要对脐带缆系统进行静态分析。静态分析问题是分析在静态力和力偶作用下脐带缆的响应,与时间无关。脐带缆静态分析时的假设条件是母船静止,即母船升沉的位移、速度与加速度均为零,脐带缆由初始无拉伸状态释放,在外力作用下最终到达平衡状态。

在海平面上某点建立固定的空间坐标系Oxyz,对应的空间基矢量分别为e1、e2、e3,材料坐标系OXYZ与空间坐标系重合,对应的基矢量分别为E1、E2、E3。分析深度分别取2000、4000、6000、8000 和10 000 m,水下铠缆初始位于X轴上,初始缆索单元长度均为10 m,采用2 节点线性等参插值。仿真获得脐带缆三维空间位置和形状如图4 和图5 所示。

图4 静态条件下水下脐带缆的位置和形状

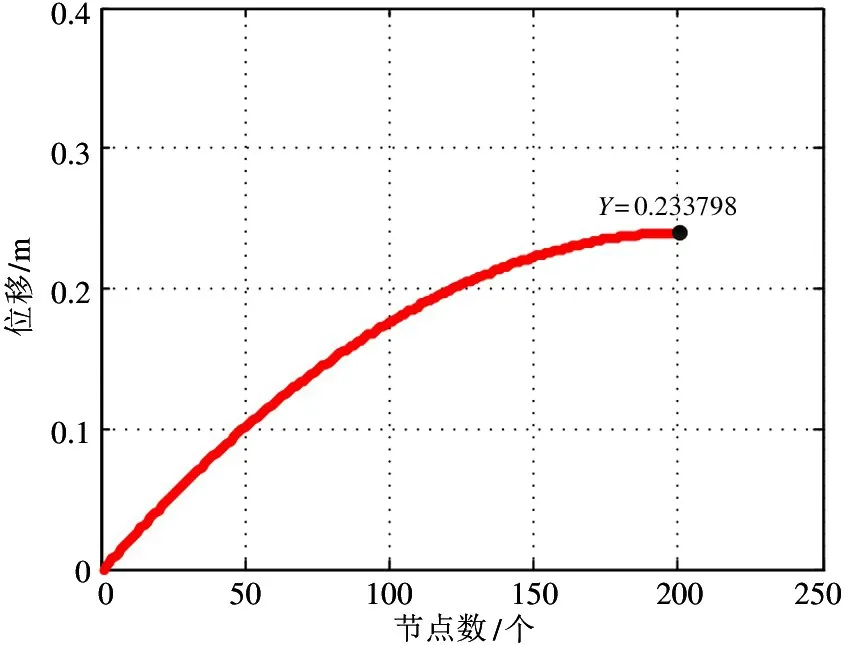
图5 静态条件下水下脐带缆的位置和形状

为了初步验证所建立有限元模型的正确性,下面给出静态条件下水下缆索的静态伸长量。若设浸没于水下的缆索长度L=2000 m,已知缆索的轴向刚度EA=4.32 ×107 N,则整个缆索的弹性刚度k=EA/L(N/m)。水下缆索力的平衡方程为

式中,FG表示水下缆索与ROV 的有效总重力,FB表示水下缆索与ROV 的有效总浮力,分别表示为

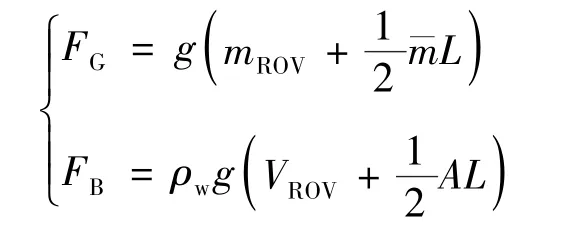
图6 是经有限元程序求解出的缆索末端4 个节点的位移值。由图可知缆索最末端节点的位移为0.240 637,与理论解析解0.240 74 非常接近,说明了有限元程序静态条件下分析的正确性。其他深度静态分析结果及与解析解的对比结果如表2 所示。 由图7可知,静态条件下水下缆索各节点的位移与对应的节点间的关系并不符合线性关系,由于缆索首端承受的重量最大而末端承受的重量最小,缆索上面越靠后的节点变形越小,对应着图上各曲线逐渐变小的斜率变化。由于缆索节点变形量是逐节点积累的,因此缆索末端的节点位移是最大的。

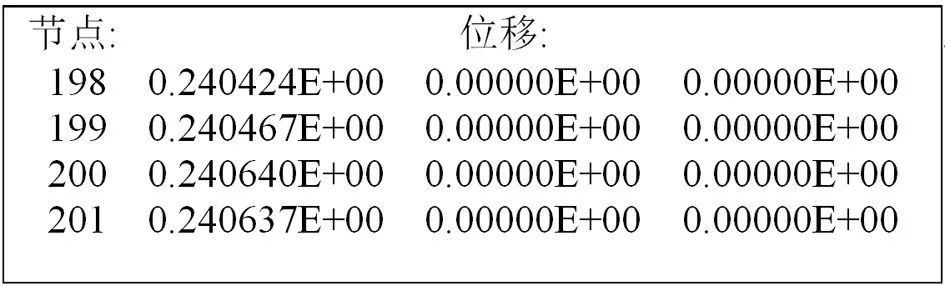
图6 有限元程序输出的缆索末端4 个节点的位移分量

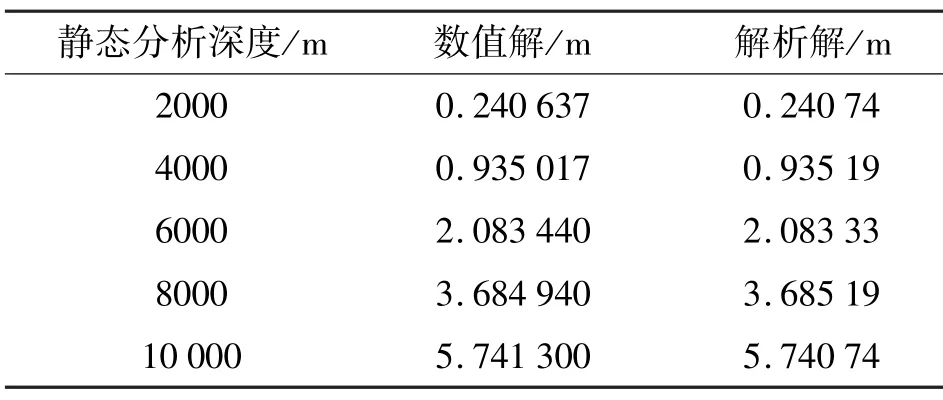
表2 有限元程序输出的缆索末端4 个节点的位移分量

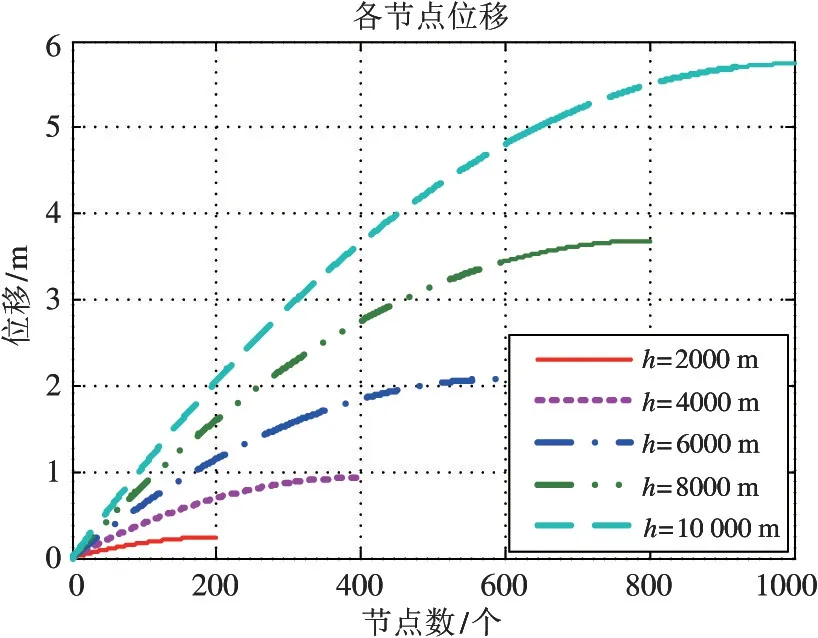
图7 不同深度下缆索各节点的竖向位移

3.4 无母船升沉和有恒定海流时的静态分析

海流对水下脐带缆系统的安全工作性能会产生不可忽视的影响。为获得海流对水下脐带缆的影响,将海流进行一定的简化,假定海流恒定,且从海面到海底逐渐减小,海底处为零。分析在不同深度和不同海流流速下的水下脐带缆的稳态构型。分析深度分别为4000、6000、8000 和10 000 m,在每个深度下的海流流速分别取为0.1、0.3、0.5 和0.7 m/s。图8 所示为下潜深度1000 m、海流速度0.1 m/s 时,脐带缆水下构型随时间的变化规律。由图可知,仿真初始阶段,脐带缆中上部(1000 m 深度)沿着海流方向发生水平偏移,末端位移较小;随着时间的推移,脐带缆末端位移逐渐增大,缆构型逐渐趋近稳定状态;当仿真时间达到1000 s 时,基本达到稳定状态;此时缆末端的竖直偏移量为10 m,水平位移约为52 m。与金属铠装脐带缆相比偏移量增大非常显著,可见海流对全海深ROV 非金属铠装脐带缆系统有较大影响。

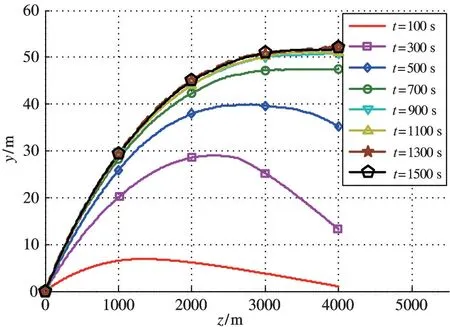
图8 铠缆水下构型随时间变化曲线(深度1000 m、海流速度0.1 m/s 时)

下潜深度4000 m 时脐带缆在不同海流影响下的稳态构型如图9(a)所示。当海流v0=0.1 m/s 时脐带缆末端的水平偏移只有52 m,竖直偏移量为3 m;v0=0.3 m/s 时脐带缆末端的水平位移为141 m;v0=0.5 m/s 时脐带缆末端的水平位移为264 m;当v0=0.7 m/s 时脐带缆末端的水平位移达到了384 m。到了6000 m 深度时,脐带缆末端的水平偏移量大于4000 m 时的情形,而8000 m 时相同海流作用下铠缆末端水平偏移量大于6000 m 情形,而10 000 m时相同海流作用下铠缆末端水平偏移量又要大于8000 m 情形,如图9(b)、9(c)和9(d)所示。其主要原因是水下脐带缆的重量会随着深度增加而增加,而海流对缆索作用力的增加幅度明显要大于脐带缆重量的增加幅度,所以铠缆的水平偏移量会随着深度的增加而增大。

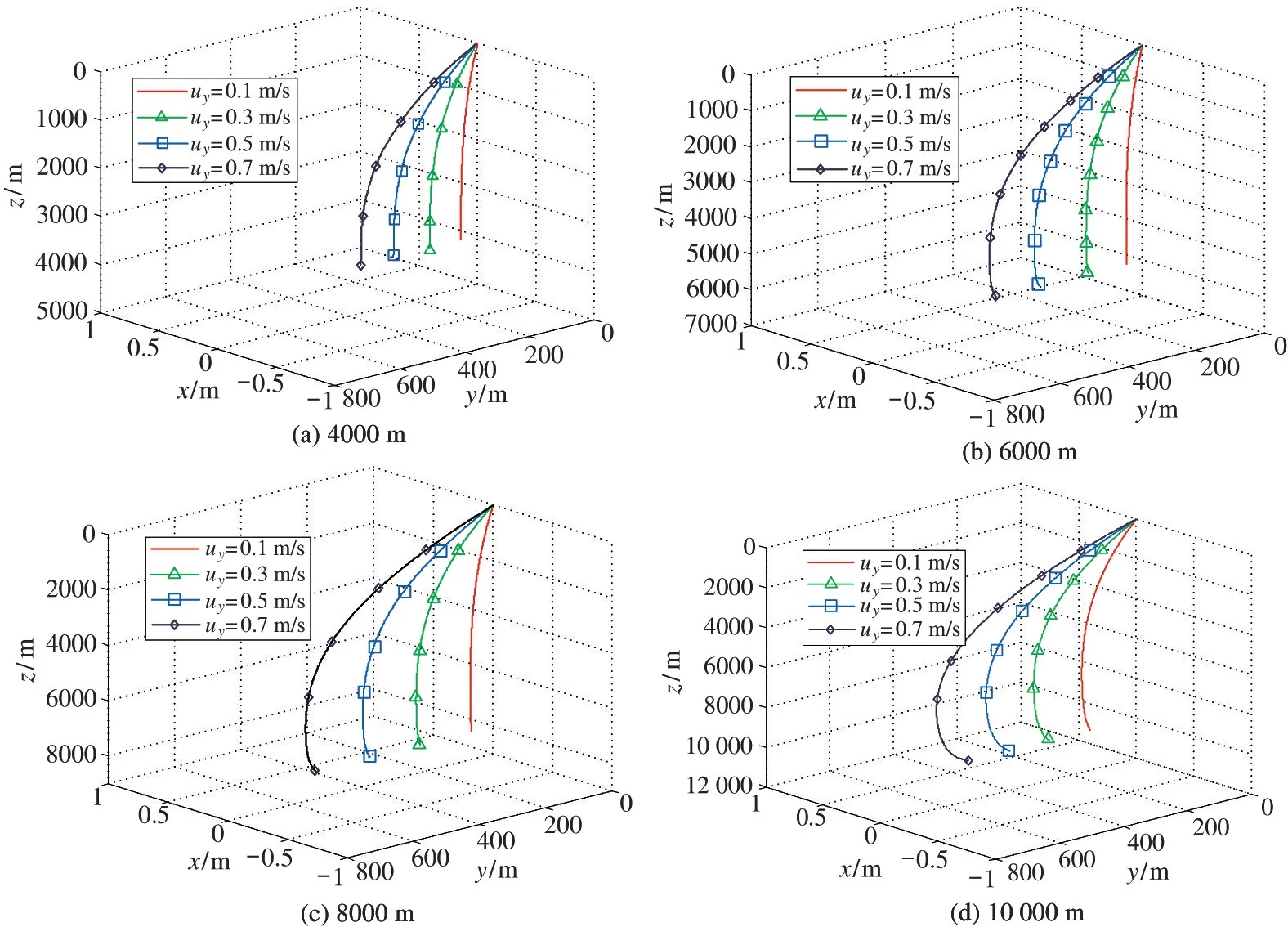
图9 铠缆水下构型随时间变化曲线

脐带缆在稳态海流和无母船升沉条件下的稳态分析是与时间无关的平衡问题,由于假设海流恒定,作用时间无限长,由此得出的脐带缆末端偏移量与实际动态结果相差较大,因而仅具有理论上的参考意义。

3.5 母船升沉激励时铠缆系统动态特性

前节对水下脐带缆系统进行了静态分析,得到的稳态平衡值可作为动态分析的初始值,包括水下缆索的初始长度和初始节点位移等。水下脐带缆是一个随时间不断变化的动态系统,受诸多内部和外部因素的影响,其动态特性非常复杂。本节分析全海深脐带缆在母船升沉激励下的动态响应。全海深脐带缆动态特性主要包括铠缆内部张力及铠缆两端的位移、速度及加速度随着时间的动态变化情况。

设母船仅做升沉运动,幅值为1 m,周期为8 s,忽略母船在海上的水平位移与转动。将母船的升沉位移、速度与加速度作为运动边界条件施加在缆索的首单元节点上。深度分别为1000、2000、4000、6000、8000、10 000 m。运行有限元程序,得到在四级海况下正弦母船升沉激励不同深度下的脐带缆动态响应,其中4000、6000 和10 000 m 仿真结果如图10、图11 和图12 所示。

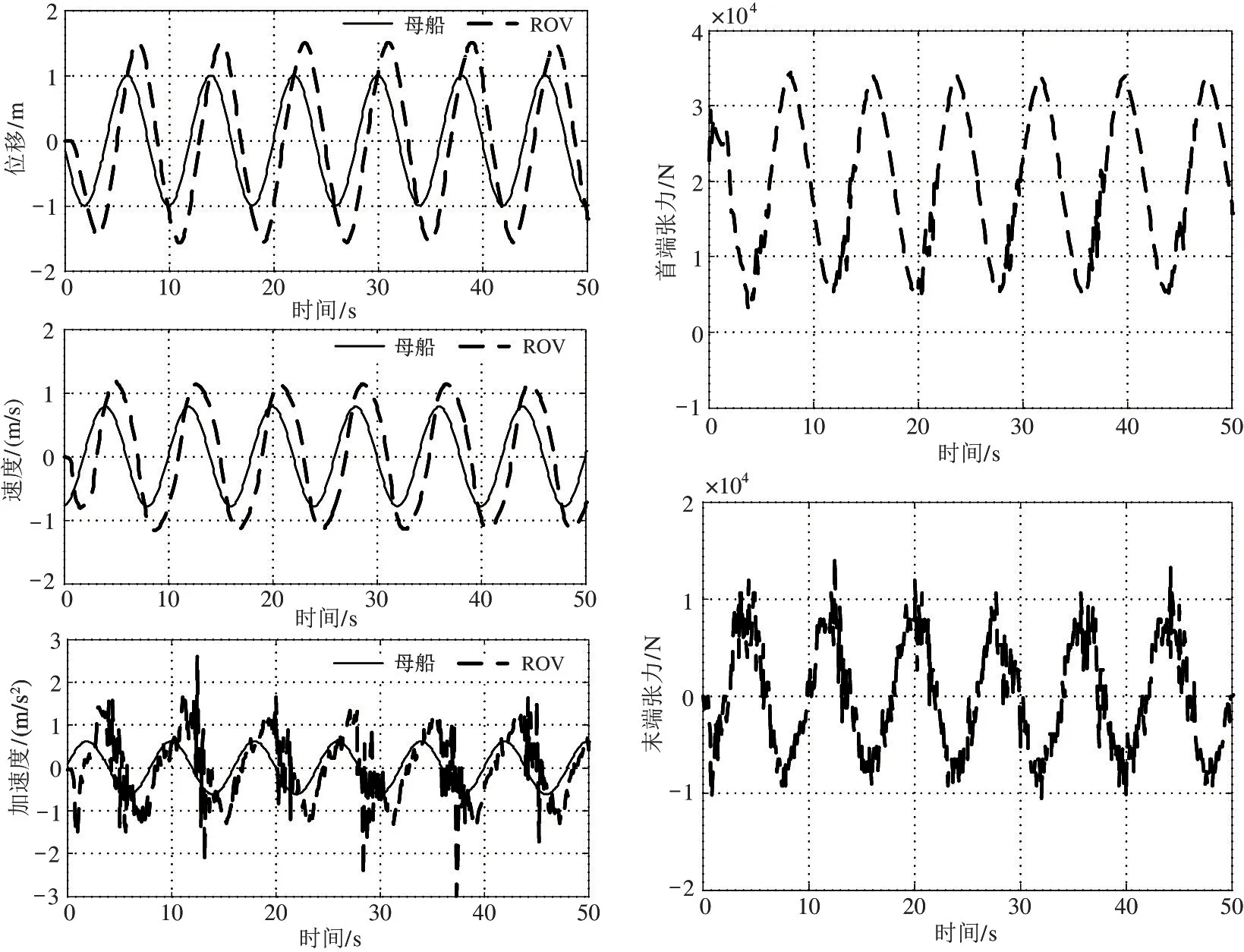
图10 正弦升沉激励时母船与ROV 升沉对比及铠缆首端张力波动(4000 m)

由图11 可知,当下潜深度大于4000 m 后,随着深度增加运动相位滞后逐渐增加,但ROV 升沉运动幅值的放大幅度呈逐渐减小趋势。由图12 可以看出,当释放深度达到10 000 m 时,ROV 的升沉运动幅度已经减小到与母船基本一致;铠缆首端的张力随着释放深度持续增加,当ROV 下潜到10 000 m 最大潜深时,铠缆的最大张力均值为49.2 kN,最大张力约为57.9 kN,均小于铠缆的安全工作载荷66 kN;因此在给定的母船升沉运动条件下,全海深ROV 非金属铠装脐带缆可以满足安全使用要求。

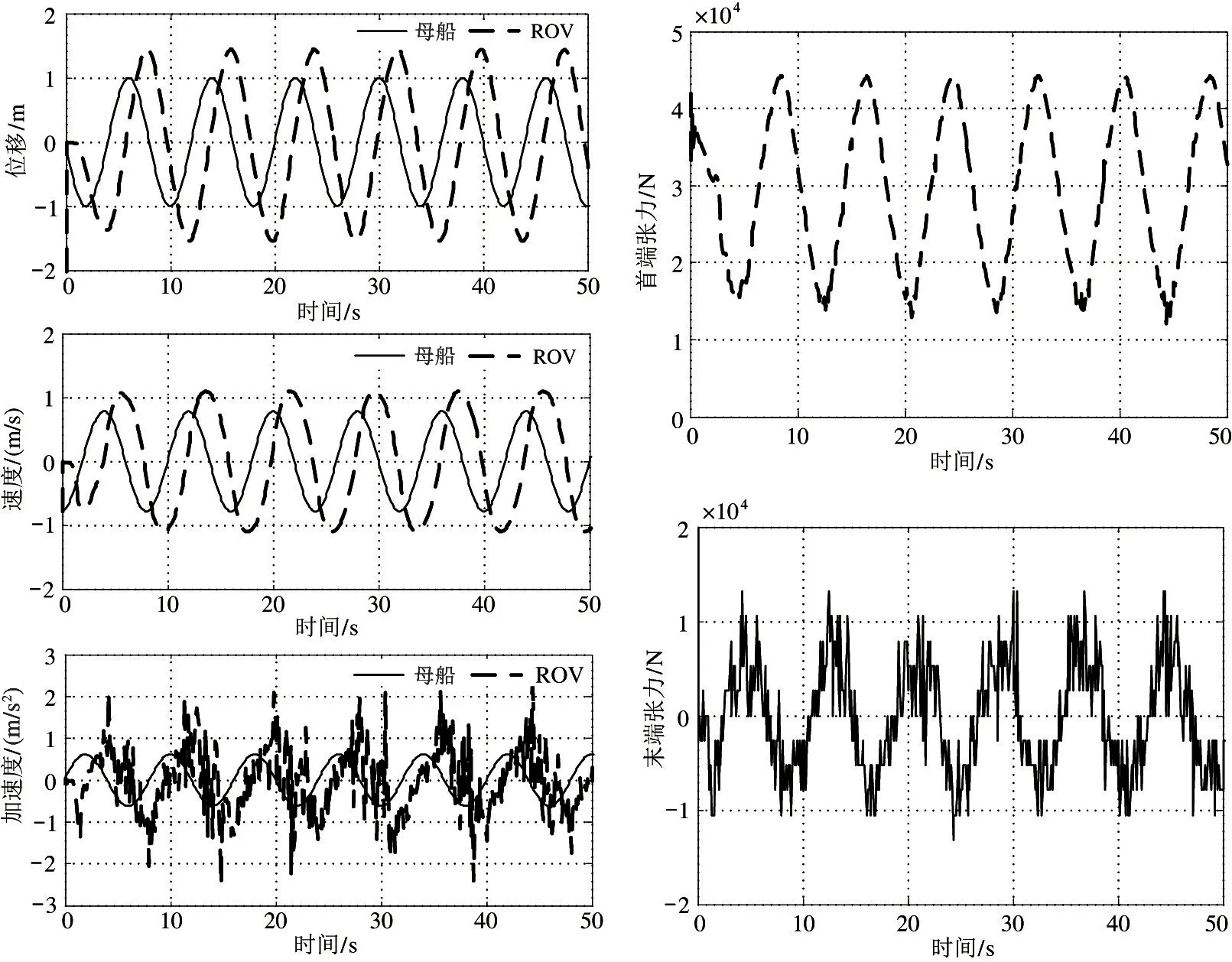
图11 正弦升沉激励时母船与ROV 升沉对比及铠缆首端张力波动(6000 m)

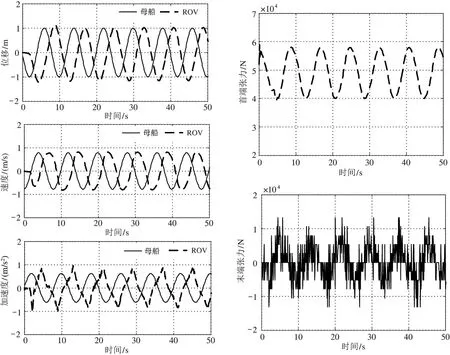
图12 正弦升沉激励时母船与ROV 升沉对比及铠缆首端张力波动(10 000 m)

母船的正弦升沉激励通过脐带缆传递给ROV,使得ROV 也做上下升沉运动。在水下的某段深度范围内,ROV 的振动幅度会被放大到最大,同时铠缆张力波动幅值也增至最大,这样的深度范围为脐带缆的共振区域,确定该区域对于深海ROV 系统的安全工作是至关重要的。本节的主要目的是通过正弦激励时水下铠缆系统动态特性的分析,识别出在该激励条件下整个系统的共振区域,从而为制定避开共振区域的措施提供参考。

与母船升沉运动相比,不同潜深下ROV 升沉运动的滞后时间与升沉幅度放大比例如图13 和图14所示。由图10 可知,在1000 m 潜深时ROV 的平均滞后时间接近于零,说明该情形时ROV 与母船的运动几乎是同步的,随着深度的增加,ROV 的平均滞后时间逐渐增加,5000 m时平均滞后时间约为1.4 s,到11 000 m 时ROV 的平均滞后时间约为3.1 s。从图10～图12 中还可以看出,在4000 m 以下潜深时,ROV 的最大滞后时间要小于1 s;而从4000～6000 m深度范围内,ROV 的最大滞后时间则在1～2 s 内变化。同时,ROV 的升沉运动与母船升沉运动幅值之比从1000 m 开始逐渐大于1。在1000～5000 m 的深度范围内,ROV 的平均放大倍数一直是递增的,从5000 m 后开始递减,到10 000 m 时ROV 运动幅值几乎跟母船相同,从10 000 m 开始,放大倍数小于1。这一变化趋势也说明了水下铠缆系统在5000 m左右的深度发生了幅值较大的共振现象,当远离这一共振深度范围时,ROV 的升沉幅值会明显降低。尽管ROV 升沉幅值在水下是放大的,但并不是无限放大的,在1000～10 000 m 深度范围内,ROV 升沉运动的放大倍数始终在1～1.5 单位之间变化,而超过10 000 m 后幅值放大效应基本消失。

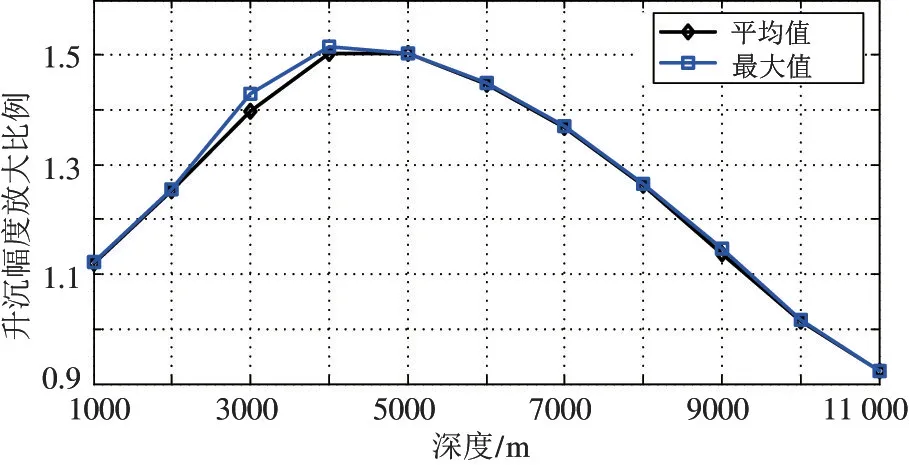
图13 正弦激励时不同潜深下ROV 升沉放大比例

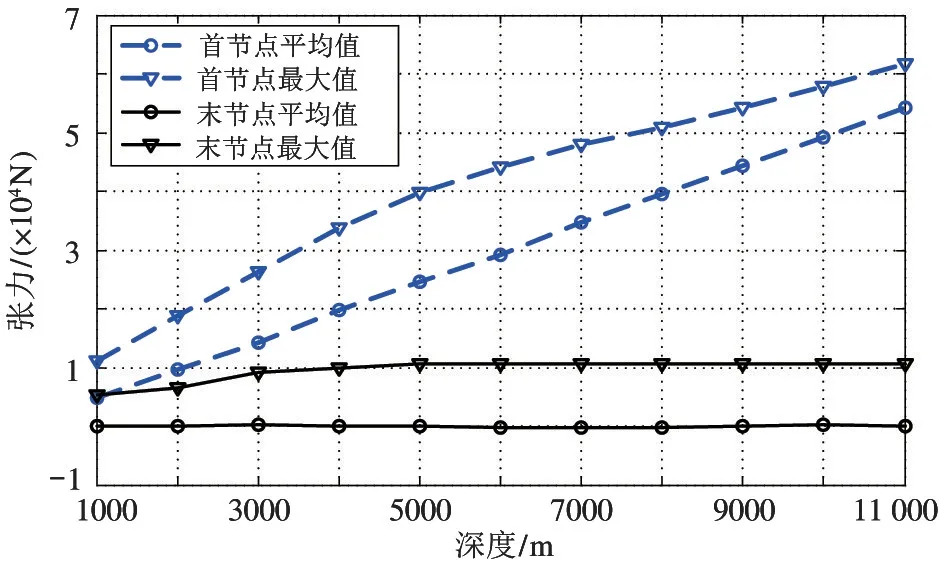
图14 正弦激励时不同潜深的铠缆首末两端张力均值与最值

不同潜深下铠缆顶端张力围绕着张力均值上下波动,而顶端张力均值应等于实际的静态张力,它是水下铠缆重量与ROV 重量的总和。铠缆顶端张力均值随着潜深的增加而线性增加,1000 m 时铠缆顶端张力均值均为4.8 kN,而到11 000 m 时均值已达到了54.1 kN,是1000 m 时的11 倍多,如图13 所示。顶端张力在11 000 m 深度达到了最大,约为61.8 kN,极为接近该铠缆的最大安全工作载荷(66 kN),因此在该海况下工作需要有可靠的安全保障,如增加升沉补偿系统等。而铠缆低端张力最值均相差不大,由于铠缆底端仅与ROV 相连,因此铠缆底端张力均值非常接近ROV 的水中重量,均值曲线基本呈水平状。

如图15 所示,顶端张力标准差与底端张力标准差均在5000 m 深度时达到峰值,说明此处的张力波动幅度最大,原因正如前面所述——在5000 m 左右深度范围整个水下铠缆系统发生了幅度最大的共振现象,因此在实际工作时深海ROV 系统应快速穿过5000 m 左右深度的共振区域,避免由共振所带来的损坏。

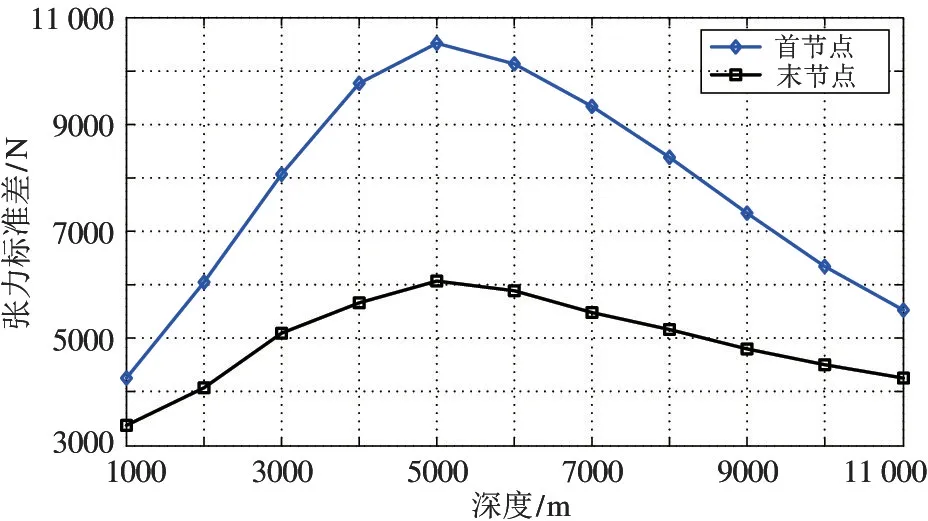
图15 正弦激励时不同潜深下铠缆两端张力标准差

4 结论

本文基于几何精确梁理论,建立了三维非线性脐带缆的有限元模型,基于该模型对全海深ROV 非金属铠装脐带缆动力学性能进行了分析,得到以下结论。

(1)ROV 下潜到10 000 m 潜深时,脐带缆的最大张力均值为49.2 kN,最大张力约为57.9 kN,均小于缆的安全工作载荷66 kN。全海深脐带缆的设计满足要求。

(2)5000 m 左右潜深为全海深ROV 非金属铠装脐带缆系统的共振区域,实际应用时应尽快穿过该区域,避免共振带来的系统损坏。

(3)海流的作用对脐带缆空间动态形状的影响至关重要,但不影响水下脐带缆系统的共振放大区域的产生。