一种新型垂直分腔颗粒阻尼器振动特性分析研究

周占学 于 爽 李 杨 袁晓聪 张 波

(1.河北建筑工程学院，河北 张家口 075000；2.河北省土木工程诊断、改造与抗灾重点实验室)

0 前 言

颗粒阻尼器是一种利用颗粒间碰撞及颗粒摩擦消耗受控结构振动的被动阻尼器[1].颗粒阻尼器分为堆积型颗粒阻尼器与非堆积型颗粒阻尼器，非堆积型颗粒阻尼器分为单层颗粒阻尼器[2]与多层颗粒阻尼器[3].颗粒阻尼器对结构的消能减振作用需要仔细的分析和设计参数，如颗粒的尺寸和形状、密度、外壳的尺寸和形状、主系统的激励类型，以及许多其他因素都是重要的阻尼性能[4].

因颗粒阻尼器属于高度非线性行为且影响因素十分复杂，本文将采用离散单元法研究颗粒运动的力学行为，并通过颗粒接触模型计算颗粒的接触力与弯矩.

1 数值模拟方法

EDEM是基于离散单元法模拟和分析的CAE软件，它可以管理设置每个颗粒个体(形状、质量、速度、温度等)及施加在颗粒上的力的信息，导入真实颗粒体的CAD模型.EDEM可以与CAE结合来模拟粒子与电磁场、粒子与流体、粒子与结构的相互作用.EDEM还可以应用在如下领域：颗粒混合与分散；颗粒收缩、断裂及膨胀；颗粒粘性和塑性力学；颗粒热和质量的传递；颗粒腐蚀；颗粒从固-液体系中的去除.

1.1 主系统的控制方程

建立系统有限单元集合的运动方程，并假设x为在垂直方向上的位移，则运动方程为：

(1)

在式(1)中，M为受控结构的质量矩阵；K为受控结构的刚度矩阵；C为受控结构的固有阻尼矩阵；f为与颗粒碰撞的总碰撞力；F为作用在上的外力矢量.力学简图如图1所示.

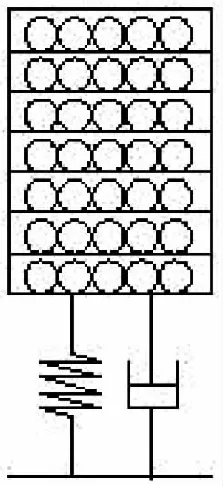
图1 力学简图

1.2 颗粒之间接触力计算

根据Hertz接触理论，法向力Fn表示为：

(2)

在式(2)中，V=va-vb；kn和cn是a颗粒的法向弹性系数和法向阻尼系数；α是法向重叠量；v是颗粒a相对颗粒b的速度，n是发生碰撞时从颗粒a球心到颗粒b球心的法向单位矢量.

根据Hertz接触理论，切向力Ft表示为：

Ft=-ktδ-ctvct

(3)

在式(3)中，kt、ct是切向弹性系数和切向阻尼系数；vct是接触点的滑移速度；δ是接触点的切向位移.

滑动速度矢量vct为：

vct=v-(v·n)n+Rαωα×n+Rbωb×n

(4)

在式(4)中，Ra和Rb分别是颗粒a和颗粒b的半径；ωa和ωb分别是颗粒a和颗粒b的角速度.

若下列关系成立:

|Ft|>μs|Fn|

(5)

则颗粒a发生滑动，切向力为

Ft=-μs|Fn|nt

(6)

式(6)式库伦摩擦定律；μs是静摩擦系数.

切向单位矢量n，由下式确定：

(7)

颗粒a受到的合力和合力矩为：

F=Fn+Ft,M=Ra×n×FT

(8)

1.3 弹性系数的确定

法向弹性系数kn由Hertz接触理论确定：

(9)

式(9)中，Ea、Eb和va、vb分别是颗粒a和颗粒b的弹性模量和泊松比；Ra、Rb分别是颗粒a和颗粒b的半径.

如果颗粒a和颗粒b属于同种材料且粒径相等，则kn简化为：

(10)

切向弹性系数kt由下式确定：

(11)

如果颗粒a和颗粒b属于同种材料且粒径相等，则kt简化为：

(12)

1.4 阻尼系数的确定

质量为m的弹簧振子如果处于临界阻尼状态，则机械能以最快速度衰减，此时法向阻尼系数为：

(13)

切向阻尼系数为：

(14)

2 仿真模型建立及结果分析

2.1 模型参数

颗粒阻尼器仿真模型如图2所示，颗粒阻尼器尺寸：长×宽×高=140mm×100mm×140mm，颗粒阻尼器分成垂直的7个腔室，每个腔室尺寸：长×宽×高=140mm×100mm×20mm.仿真模拟将采用颗粒半径分别为4mm、6mm、8mm.颗粒材料密度：钢球的密度7850ρ/(kg·m-3)、刚玉球的密度7900ρ(kg·m-3)，激振频率f为10HZ、15HZ、20HZ.同时设有对照组(非阻塞性颗粒阻尼器，Non-obstructive Particle Damper NOPD)如图3所示.对照组容器尺寸：长×宽×高=140mm×100mm×140mm.

图2 新型颗粒阻尼器 图3 对照组

2.2 结果分析

2.2.1 新型阻尼器与对照组

首先堆积型和新型颗粒阻尼器的耗能机理是通过颗粒间的摩擦和非弹性碰撞以及动量交换来耗散能量.堆积型颗粒阻尼器颗粒堆积在一起，颗粒间相对运动程度对振动幅值的变化特别敏感，随着振动幅值的减小，损耗能量可以忽略.然而新型颗粒阻尼器相对于堆积型颗粒阻尼器启振条件更容易，也更加容易发生相对运动.当振动幅值较小颗粒与容器壁不发生碰撞时，颗粒间通过摩擦耗能与碰撞耗能产生的阻尼效应减轻结构的振动.如表1分别利用颗粒动能、法向力、切向力三个参数分析垂直分腔颗粒阻尼器与NOPD振动性能对比，从表中可以看出无论是动能还是法向力、切向力非堆积型颗粒阻尼器减振性能都要优于堆积型颗粒阻尼器.

表1 新型阻尼器与对照组响应结果

2.2.2 颗粒振动特性分析

分别选取半径为4mm、6mm、8mm三种不同的颗粒半径进行仿真实验，每种颗粒距离腔室壁的距离采用并联式单向单颗粒阻尼器力学模型及优化分析文中[5]的方法，分别取值2.3mm、3.5mm、4.1mm.图4为颗粒半径不同对颗粒累计接触动能的影响.由图可知，在其它条件相同时，半径为8mm的颗粒累计接触动能高于半径为4mm、6mm的颗粒，对结构整体的消能减震作用更明显.如图5可以看出控制其它条件相同改变颗粒密度，颗粒密度越大颗粒碰撞产生的累计动能越多，同时也再次证明颗粒粒径对颗粒动能的影响，颗粒粒径越大颗粒碰撞获得的动能越多.如图6当保证颗粒粒径、颗粒密度相同，在20HZ频率作用下颗粒得到的动能高于10HZ、15HZ的频率作用，说明外界激励强度对颗粒碰撞剧烈程度具有影响作用.

图4 颗粒半径-颗粒累计接触动能 图5 颗粒密度-颗粒累计接触动能

图6 激励频率-颗粒累计接触动能

3 结 论

本文通过离散元仿真分析了一种新型颗粒阻尼器，分别对颗粒粒径的大小、颗粒密度不同、外界激励强度对阻尼器的影响进行研究.

可以得到以下结论：

1)对于颗粒粒径不同的颗粒，粒径越大颗粒碰撞获得动能越大，其法向力、切向力也越大.

2)当颗粒密度不同时，随着颗粒密度的增加颗粒之间的摩擦耗能和碰撞耗能以及动量交换也在增加.

3)相对其他影响因素外界激励强度的变化会使得颗粒与颗粒、颗粒与容器壁的动能变化更加明显，外界激励强度越大颗粒运动越剧烈.也可以说地震的震级越高阻尼器的耗能能力越强.