一类时滞SDTR戒酒模型的局部渐近稳定性

张子振，张伟诗，宋志强

(1.安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030；2.呼伦贝尔学院 机电工程学院，内蒙古 呼伦贝尔 021008)

近年来，随着生活水平的提高，生活方式越来越多样化，饮酒在人们的日常生活中扮演着越来越重要的角色。2018《中国饮酒人群适量饮酒状况》白皮书数据显示，我国饮酒人群高达6亿[1]。然而，与之相应的与饮酒相关的各种疾病也大大增加,比如，脂肪肝、冠心病、酒精依赖综合征、酒中毒性幻觉症等,酗酒还会引起家庭暴力、酒后驾驶等社会不良问题[2]。因此，饮酒尤其是酗酒不仅是一个严重的全球性公共卫生问题，也是一个亟待解决的社会问题。为了控制酗酒行为传播，近年来，一些研究学者开始借助于动力学系统模型研究酗酒行为的传播规律，以便为控制酗酒行为的传播提供参考性建议。Xiang等[3]提出了一类考虑移民影响的戒酒模型，通过构造合适的李雅普诺夫函数研究了模型的全局渐近稳定性。Ma和Huo[4]提出了一类考虑公共健康教育的戒酒模型，并研究了模型的全局渐近稳定性，分析了公共健康教育对酗酒行为传播控制的影响。最近，文献[5]研究了一类具有时滞的戒酒模型

(1)

其中:S(t)表示偶尔饮酒人群在时刻t的数量,D(t)表示酗酒人群在时刻t的数量,T(t)表示戒酒人群在时刻t的数量,R(t)表示成功戒酒人群在t时刻的数量;A，β1，β2，μ，η，δ1，γ，δ2，σ为模型(1)的参数，其具体含义可以参看文献[5];τ表示戒酒人群成功戒酒需要的时间周期时滞。文献[5]研究了时滞τ对模型(1)稳定性的影响，分析了模型(1)Hopf分岔的存在性。

受文献[5]研究工作的启发，并考虑到成功戒酒人群对酒精的临时免疫力，本文考虑另外一种形式的时滞戒酒模型

(2)

其中，τ为成功戒酒人群对酒精的临时免疫期时滞。

1 基本再生数

求解方程组

(3)

2 局部渐近稳定性

根据文献[5]的分析可知，当R0>1时，模型(2)存在唯一饮酒平衡点E*(S*,D*，T*,R*),其中

其中D*是方程

(4)

的正根,式中

l1=Aβ1β2(μ+η)+β1ησγ-β1γ(μ+η)(μ+δ2+σ)-[β1(μ+δ2+σ)+β2μ](μ+η)(μ+δ1),

l2=-β1β2(μ+δ1)(μ+η),l0=μ(μ+η)(μ+δ2+σ)(μ+δ1+γ)(R0-1)。

显然，l2<0。当R0>1时，l0>0。因此，当R0>1时，方程(4)存在唯一正根。进而可以得知，R0>1时，模型(2)存在唯一饮酒平衡点E*(S*,D*,T*,R*)。

模型(2)在E*(S*,D*,T*,R*)处的线性化部分为

(5)

相应的特征方程为

λ4+Γ3λ3+Γ2λ2+Γ1λ+Γ0+(Φ3λ3+Φ2λ2+Φ1λ+Φ0)e-λτ=0。

(6)

其中

μ(μ+β1D*)(β1S*+β2T*-μ-δ1-γ)(β2D*+μ+δ2+σ),

μ(μ+β1D*)(β2D*-β1S*-β2T*+2μ+δ1+δ2+σ+γ)-

(2μ+β1D*)(β1S*+β2T*-μ-δ1-γ)(β2D*+μ+δ2+σ),

μ(μ+β2D*)+(2μ+β1D*)(β2D*-β1S*-β2T*+2μ+δ1+δ2+σ+γ),

Γ3=(β1+β2)D*-β1S*-β2T*+4μ+δ1+δ2+σ+γ,

η(μ+β1D*)(β1S*+β2T*-μ-δ1-γ)(β2D*+μ+δ2+σ),

η(μ+β1D*)(β2D*-β1S*-β2T*+2μ+δ1+δ2+σ+γ),

Φ2=η(2μ+β1D*)(β1D*-β1S*+β2D*-β2T*+3μ+δ1+δ2+σ+γ),Φ3=η。

当τ=0时，方程(6)变为

λ4+(Γ3+Φ3)λ3+(Γ2+Φ2)λ2+(Τ1+Φ1)λ+Γ0+Φ0=0。

(7)

根据Routh-Hurwitz稳定性判据，当(Γ0+Φ0)>0，(Γ2+Φ2)(Γ3+Φ3)>(Γ1+Φ1)，且

(Γ1+Φ1)(Γ2+Φ2)(Γ3+Φ3)>(Γ0+Φ0)(Γ3+Φ3)2+(Γ1+Φ1)2

时，模型(2)局部渐近稳定。

当τ>0时，假设λ=iε(ε>0)为方程(6)的根，代入方程(6)分离实部和虚部，有

(8)

进而可以得到下列关于ε的代数方程

(9)

令

方程(9)变为

χ4+Δ3χ3+Δ2χ2+Δ1χ+Δ0=0。

(10)

(11)

其中

对方程(6)两边求λ关于τ的导数，得到

因此

定理1对于模型(2)，如果R0>1，那么当τ∈[0,τ0)时，模型(2)局部渐近稳定；当τ=τ0时，模型(2)在饮酒平衡点E*(S*,D*,T*,R*)处产生Hopf分支。

3 数值模拟

选取A=0.7，β1=0.8，μ=0.25，η=0.45，β2=0.3，δ1=0.35，γ=0.4，δ2=0.3，σ=1.25。可以得到模型(2)的如下示例模型：

(12)

利用Matlab软件计算得到R0=2.24>1，进而计算得到示例模型(12)的唯一饮酒平衡点

E*(1.2118,0.4936,0.1014,0.1811)。

当τ=0时，可以计算得到Γ0=0.1777，Γ1=1.1068，Γ2=1.9106，Γ3=2.8431，Φ0=0.3198，Φ1=0.7131，Φ2=1.1279，Φ3=0.45。进而可以验证

(Γ0+Φ0)>0，(Γ2+Φ2)(Γ3+Φ3)>(Γ1+Φ1)，

(Γ1+Φ1)(Γ2+Φ2)(Γ3+Φ3)>(Γ0+Φ0)(Γ3+Φ3)2+(Γ1+Φ1)2。

因此，当τ=0时，示例模型(12)局部渐近稳定。仿真效果如图1所示。

图1 当τ=0时的仿真效果

当τ>0时，可以计算得到ε0=0.4631，τ0=8.0819，G′(χ0)=0.1068>0。因此，根据定理1可知，当τ∈(0,τ0)时，示例模型(12)局部渐近稳定，仿真效果如图2所示。

图2 当τ=6.75∈(0,τ0)时的仿真效果

当τ=τ0时，示例模型(12)在E*(1.2118,0.4936,0.1014,0.1811)处产生Hopf分支，仿真效果如图3所示。

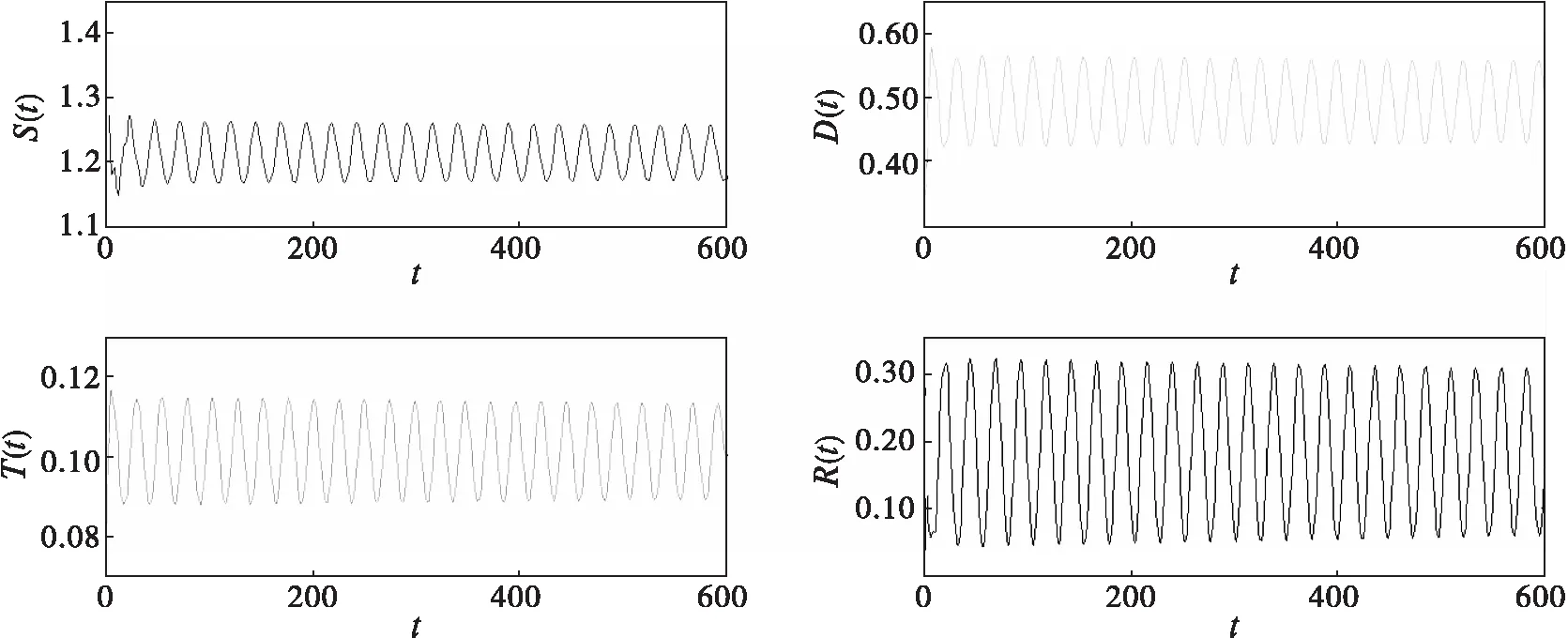
图3 当τ=9.85>τ0时的仿真效果

4 小结

适度饮酒有利于帮助饮酒者缓解压力和紧张情绪，然而过度饮酒甚至酗酒不仅会给饮酒者的身体带来伤害，而且还会给社会治安带来安全隐患。基于此，本文在文献[5]的基础上，研究了一类时滞SDTR戒酒模型。

首先计算得到模型的基本再生数，并计算得到模型的饮酒平衡点。进而以戒酒成功者对酒精的临时免疫期时滞为分支参数，推导出模型局部渐近稳定和产生Hopf分支的充分条件。研究表明，戒酒成功者对酒精的临时免疫期时滞越小(低于时滞临界点τ0)，越有利于控制酗酒行为的传播;而当戒酒成功者对酒精的临时免疫期时滞超过临界点τ0时，酗酒行为将失去控制。本文所得结果是对文献[5]研究工作的适当补充。