指数比率局部保持投影健康状态监控方法及其半导体蚀刻过程应用

张 成，郭青秀，李 元

(沈阳化工大学 技术过程故障诊断与安全性研究中心， 辽宁 沈阳 110142)

半导体在通信、计算机、消费电子、汽车电子、工业以及医疗等方面起着重要作用. 随着应用场景的不断拓展，半导体生产的效率以及安全性得到广泛关注[1-2].半导体蚀刻工艺过程属于典型的间歇生产过程，即将有限的物料按照一定的加工顺序，在一个或多个设备中加工，以获得有限量的产品[3].由于间歇过程能够实现小批量生产、可灵活调整生产方案与生产效率等目标，因此现代工业中，间歇生产成为发展热点.半导体蚀刻工艺过程除了具有间歇生产固有的多变量、多工序、变量时变性等特点，还有其独特的过程特征，如多中心、各模态离散程度不同等[4].由于各类传感器以及传感器系统可收集大量的半导体生产过程数据，因此基于数据驱动的过程监控方法被应用到半导体蚀刻过程中[5].

过程监控方法分为单变量过程监控和多变量过程监控.典型的单变量过程监控有Shewhart控制图、CUSUM控制图以及EWMA控制图等[6-8].单变量过程监控虽然易于理解且容易实现，但半导体蚀刻过程中变量较多，每个变量建立单独模型导致监控过程繁琐，因此多变量过程监控方法得到快速发展.主元分析(principal component analysis，PCA)及基于PCA的各类算法作为典型的多变量过程监控方法被应用于半导体蚀刻过程[9-13]，但这些方法对于半导体蚀刻过程的检测结果却不能令人满意，其主要原因是半导体数据的特征不满足PCA的监控统计量T2的假设要求[14].

针对半导体蚀刻过程的多模态特征，He等[15]利用k近邻规则(k-nearest neighbor，kNN)对其进行故障检测.结果显示：kNN算法检测效果相比于PCA有明显提升.然而半导体过程的三个模态方差不同，因此该过程的故障未被kNN全部检测出[16-17].此外，kNN由于确定近邻时需要遍历所有样本，因此计算量大同样是不能忽略的重要问题.

由于半导体蚀刻过程中变量较多，因此选取合适的降维方法可以减少监控过程的复杂度.考虑到数据的流形结构，He等[18-19]在人脸识别领域提出了局部保持投影(locality preserving projections，LPP)以及邻域保持嵌入(neighborhood preserving embedding，NPE).LPP通过构造近邻邻接图达到保持降维前后近邻关系的目的，从而找到低维空间中原始数据的流形结构.随后，Cai等[20]利用正交基函数提出了正交LPP.Chen等[21]提出二维局部保持投影，检测图像的内部流形结构.基于LPP维数约减的优势，LPP已经被引入到故障检测领域.但LPP利用的统计量T2适用于单模态过程监控，因此它对于半导体过程的监控效果不能令人满意.

针对LPP监控半导体蚀刻过程的不足，本研究提出了指数比率局部保持投影健康状态监控方法(ERLPP).首先，利用统计模量(statistics pattern analysis，SPA)将半导体三维数据展开为二维数据；其次，利用LPP将过程数据投影至特征空间；最后，通过构建新的统计量进行过程监控.多模态数据经LPP投影后仍然具有典型的多模态特征，ERLPP利用了LPP降维保持原始数据局部结构的特点.在特征空间中，通过指数比率算法将多模态数据近似融合为单一模态数据，且将数据的统计量划分在(0，1)区间的同一尺度，从而更加合理的确定控制限并完成多模态过程状态监控.

1 局部保持投影

假设数据集X包含m个n维样本点，LPP旨在寻找能够使流形结构保持的投影矩阵An×r，使高维空间中相邻的样本点xi与xj和映射到特征空间的投影坐标yi与yj依旧相邻.投影关系为

y=xA.

(1)

LPP通过构造目标函数

(2)

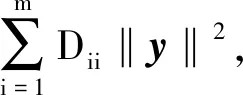
XTLXa=λXTDXa.

(3)

其中:aTXTDXa=1;L=D-W.由式(2)求出的r个最小特征值所对应的特征向量构成投影矩阵A=(a1,a2,…,ar).

LPP对过程进行监控时利用T2与平方预测误差SPE统计量，如式(4)、(5)所示：

T2=yΛ-1yT,

(4)

SPE=‖e‖2.

(5)

其中:Λ为Y的协方差矩阵,Y为特征空间的数据集；e=x-yAT.T2与SPE的控制限可由核密度估计法(kernel density estimation, KDE)确定[22].

2 指数比率局部保持投影健康状态监控方法

LPP与PCA均为典型的线性降维算法，但由于其目标函数的不同导致降维结果不同.通常，LPP要求特征空间中样本的近邻关系与原始空间样本近邻关系一致，而PCA则在主元空间中更多地保留了原始数据的信息.由于LPP在搜寻低维流形结构时考虑到原始空间中的样本近邻关系，因此LPP特征空间的数据可以保持原始数据的分布结构，例如多模态结构.但是PCA在降维时将数据离散程度最大的方向作为投影方向，这可能导致主元空间数据的分布结构改变，例如主元空间中多模态特征不明显或故障样本与正常样本无明显区分.由于LPP具有降维后可以保持数据流形结构的优势，因此LPP被引入过程监控领域.LPP在监控特征空间时采用T2统计量，而T2统计量要求数据服从多元高斯分布.当数据具有多模态特征时，T2统计量会出现故障漏报的情况，上述结论可在第三节得到验证.针对过程监控中LPP应用T2统计量的缺陷，本节提出了指数比率局部保持投影健康状态监控方法.

假设y为LPP降维后特征空间的样本点.y的指数比率统计量为

(6)

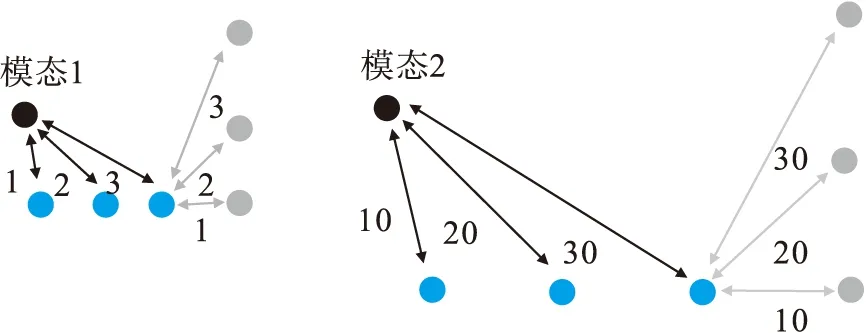
图1 多模态数据Fig.1 Plots of multimodal data

基于指数比率局部保持投影的半导体蚀刻过程故障检测策略包括两部分：离线建模与在线监测，具体如下：

(一) 离线建模

(1) 对原始数据X进行Z-SCORE标准化;

(2) 利用式(1)将X投影至LPP特征空间，记为Y;

(3) 利用式(6)计算特征空间中每个样本y的指数比率值;

(4) 根据KDE确定控制限Pucl.

(二) 在线监测：

对于测试样本xnew：

(1) 利用离线建模阶段(1)中标准化求出的均值与标准差对xnew进行标准化;

(2) 利用式(1)将xnew投影至LPP特征空间，记为ynew;

(3) 利用式(6)计算特征空间中每个样本y的指数比率值Pnew-ucl;

(4) 比较Pnew-ucl与Pucl的大小.若Pnew-ucl>Pucl，则xnew为故障样本，否则xnew为正常样本.

3 数值仿真

本节根据参考文献[16]中的多模态实例验证ERLPP算法的有效性.数据共包含三个变量x、y、z，其中前两个变量为主要变量，第三个变量为高斯白噪声，具体模型如下：

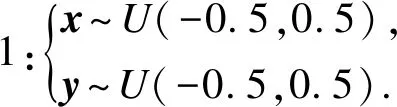
(7)

每个模态各生成100个样本用于训练模型，在同样的条件下各模态分别生成50个样本用于校验模型的有效性.通过对模态1中的变量y加入扰动得到50个故障样本，数据散点如图2所示.本节利用PCA、LPP、NPE、kNN以及ERLPP进行实验.通过累计贡献率达到90%确定PCA、LPP与NPE的主元数为2，如图3所示.kNN中k近邻个数由经验法[9]确定为5.ERLPP方法中一步近邻数k为5，二步近邻数K为19.

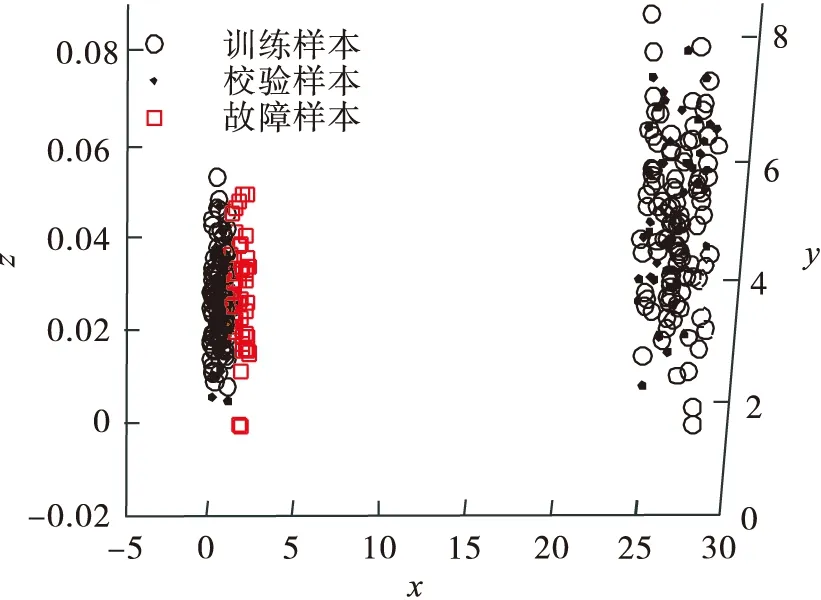
图2 数据散点Fig.2 Scatter plots of samples

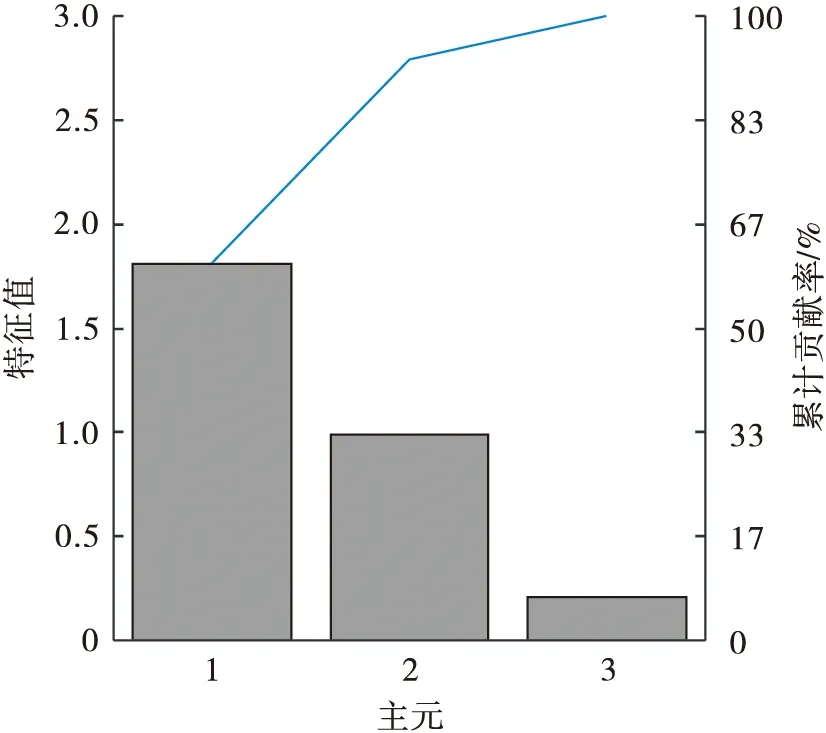
图3 PCA累计贡献率Fig.3 PCA cumulative percent variance

PCA方法检测结果如图4所示.图5为PCA主元子空间散点，可见PCA中统计量T2在二维空间呈椭圆结构.当数据为非高斯分布时，椭圆结构中会包含部分空白区域.一旦故障发生在上述空白区域，则被判定为正常样本.除此之外，PCA降维后故障样本与模态1中的训练样本出现混合现象，这将导致故障样本到原点的马氏距离与模态1中训练样本到原点的马氏距离位于同一尺度，且控制限被模态2中的训练样本统计值抬高，因此PCA方法在主元子空间的检测率为0.由于残差空间中故障样本到原点的欧式距离与正常样本到原点的欧式距离相似，因此PCA方法SPE统计量的故障检测率同样为0.

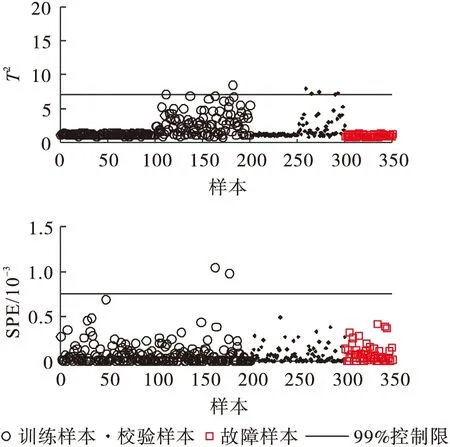
图4 PCA检测结果Fig.4 PCA fault detection results

图5 PCA主元子空间散点Fig.5 PCA principal subspace scatter

LPP与NPE方法检测结果如图6和图7所示.

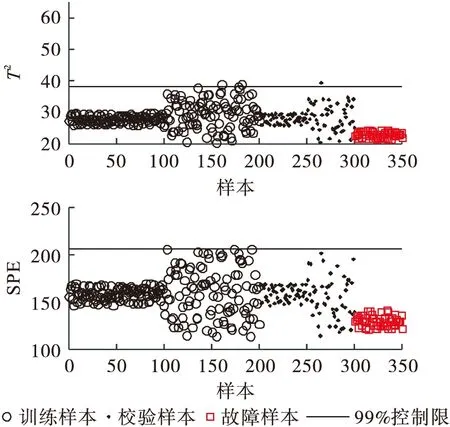
图6 LPP检测结果Fig.6 LPP fault detection results

图7 NPE检测结果Fig.7 NPE fault detection results

由图6和图7可知LPP与NPE方法检测结果与PCA相似.值得注意的是：LPP特征空间中故障样本仍然区别于正常样本，进一步验证了LPP降维后不改变原始数据的分布结构.降维结果体现了LPP的降维优势，如图8所示.

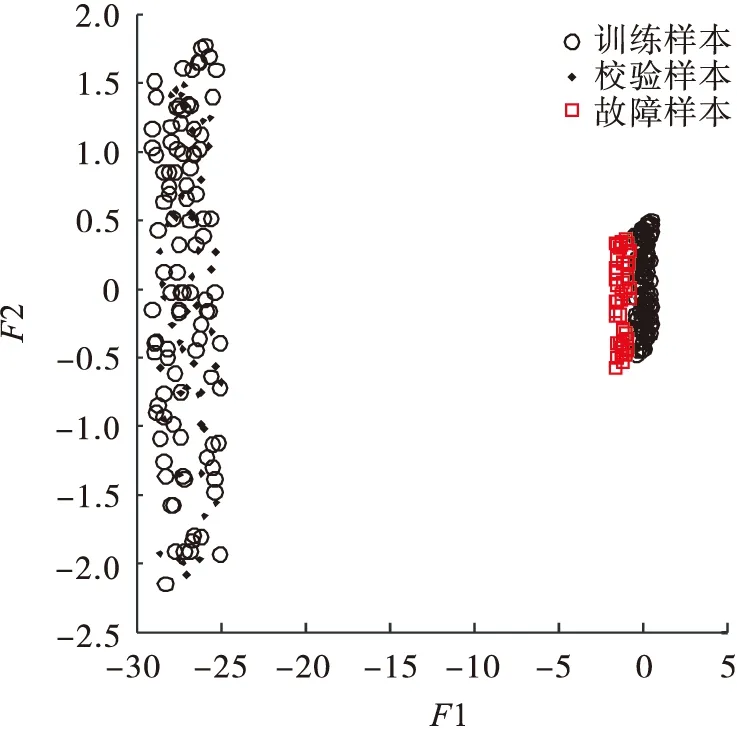
图8 LPP特征空间散点Fig.8 LPP feature space scatter

由于kNN方法进行过程监控时只考虑近邻信息，与数据结构无关，因此kNN被用来进行测试该例，其故障检测结果如图9所示.由图9可知：两个模态的训练数据统计值差异较大，稀疏模态的近邻距离和明显大于密集模态的近邻距离和，因此控制限被稀疏模态统计值拉高，导致密集模态发生的微弱故障未被成功检测.

图9 kNN检测结果Fig.9 kNN fault detection results

针对上述提及算法对多模态过程检测的缺陷，ERLPP对该例进行测试，其检测结果如图10所示.由图10可知：两个模态的训练样本被拉平到同一尺度，且均位于0～1之间，而故障样本的统计值明显大于训练样本的统计值，因此其故障检测率为100%.

图10 ERLPP检测结果Fig.10 ERLPP fault detection results

4 半导体蚀刻过程

Lam 9600金属蚀刻机上配备三个传感器来收集过程数据，分别为机器状态、射频监视器和光发射光谱学.本节采用机器状态传感器所采集的数据进行实验[23].原始数据共包含108个正常批次和21个故障批次.由于晶片缺失，因此利用107正常批次和20故障批次进行建模和检测.由于原始数据集包含批次、时间以及变量信息，为三维矩阵，现利用参考文献[24]中的SPA方法将三维矩阵转化为二维数据，如图11所示.

图11 SPA框架Fig.11 SPA framework

原始数据变量如表1所示.本节利用PCA、LPP、NPE、kNN以及ERLPP对半导体蚀刻过程进行监控，各方法参数及检测率如表2所示.

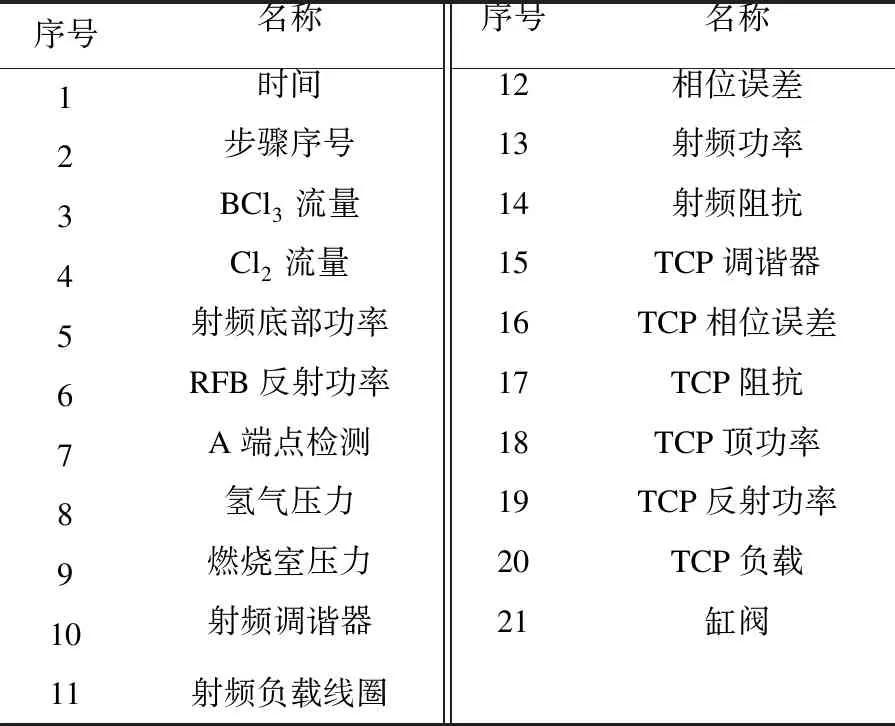
表1 变量名称Table 1 Variable name

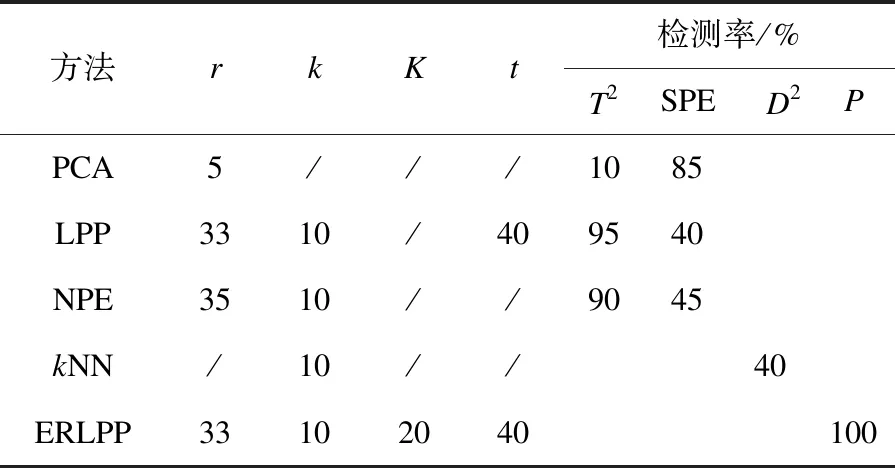
表2 参数设置Table 2 Parameter setting

PCA-T2与PCA-SPE检测率分别为10%和85%，主要原因为PCA适用于单模态过程，而半导体蚀刻过程具有典型的多模态特征.LPP与NPE虽然在降维后较好保持了原始数据的流形结构，但是半导体数据不满足统计量的假设条件，因此LPP与NPE未能检测出全部故障.

考虑到半导体蚀刻过程的多模态特征，kNN被用于测试，其检测率为40%.由于半导体蚀刻过程中数据分为三个模态，且各模态离散程度不同，因此kNN的控制限主要由离散程度较大的模态决定，导致部分故障未被成功检出.除此之外，kNN计算样本统计量时需要计算80维空间中的样本距离以确定其近邻，因此计算量较大.

针对上述提及方法对半导体蚀刻过程的检测缺陷，ERLPP被用于测试，检测结果如图12所示.通过指数比率将各个模态的统计值归到(0，1)之间，且控制限由三个模态共同决定，因此ERLPP成功检测出所有故障.

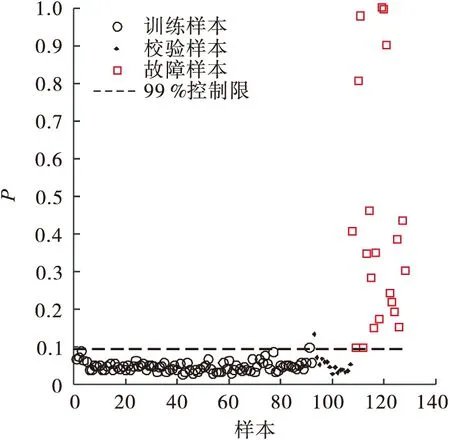
图12 ERLPP检测结果Fig.12 ERLPP fault detection results

5 结 论

针对半导体蚀刻过程的多模态且模态离散程度不同的特征，本研究提出一种新的统计量(ERLPP)来提高LPP对于半导体蚀刻过程的监控效果.ERLPP利用一步近邻距离与二步近邻距离的指数比率，消除了统计值的多模态特征，减少统计值波动，从而提高了LPP对于半导体蚀刻过程的适用性.通过仿真实验以及同类算法对比，结果验证了ERLPP的有效性.

基于本研究，下一步可研究半导体蚀刻过程故障的诊断与重构.