基于多任务贝叶斯压缩感知的探地雷达成像算法

吴 冬 晖

(安徽理工大学 电气与信息工程学院，安徽 淮南 232001)

0 引 言

步进频率连续波探地雷达(SFCW-GPR)是探地雷达系统的一种，探地雷达是一种电磁、高分辨率、物探性、非侵入性的技术，被用于扫描地下物体进行成像。由于GPR接收器通常具有超宽带宽，因此GPR信号很容易受到随机噪声的破坏。雷达分辨率取决于所使用的带宽，SFCW-GPR比脉冲雷达更具成本效益，因为它不需要过多的瞬时带宽[1-2]。因为SFCW-GPR工作频率采用的是阶梯方式步进，实现工作带宽相对所需的时间也比较长，成像速度比较慢[3]。如何有效地缩短SFCW-GPR系统的数据采集时间，提高成像效率是亟待解决的问题。提出的CS理论可以来解决这些问题，CS理论证明当信号在变换域内是稀疏的时，采样频率不必依赖于信号带宽，信号带宽主要依赖于两个基本:稀疏性和不相关性[4-5]。

对来自同一情况下的数据进行相关性分析。提出了一种基于稀疏贝叶斯学习的多任务贝叶斯压缩感知(MT-BCS)算法。该算法针对不同的任务采用了一种通用的先验层次贝叶斯分层模型，充分利用了任务之间的统计相关性，对系数向量的每个元素进行先验概率分布，限制了模型的复杂度，引入了超参数[6-8]。仿真结果表明，基于MT-BCS改进的重构算法可以同时满足计算效率和重构精度。

1 信号模型

SFCW-GPR模型如图1所示[9]，假设发射天线、接收天线和成像区域处于同一平面上，在平面沿水平方向x轴和深度方向z轴的成像，区域内的目标均匀划分为K×L网格，每个网格对应一个像素点[10]。

图1 SFCW-GPR成像模型Fig. 1 SFCW-GPR imaging model

假定选取天线测量的位置M个，频率从f0到fN-1为发射天线的一个扫描周期，其中共有N个扫描频点，P个实际散射目标数存在于检测区域[10]。在每个天线测量位置得到的复信号为

(1)

其中，m∈1,2…M,n∈1,2…N，ρp为第p个点的复反射系数，τp,m代表从第m个天线测量的位置至第p个目标点的往返传输延时。图1可以通过图2所示的列堆栈转换成KL×1维向量，记作wx。式(1)也可以用基矩阵Bm和反射系数向量wx来表示:

Sm=Bmwx

(2)

图2 网格划分示意图Fig. 2 Grid division diagram

式(2)中Sm=[s0(f0),s1(f1),…,sm(fN-1)]T是N×1维频域测量数据向量。基矩阵Bm∈N×KL，sm(fn)是天线位置在M点，工作频率为fn的回波数据。基矩阵Bm的第j列可以如下表示:

[Bm]j=[e-j2πf0τm,j,e-j2πf1τm,j,…,e-j2πfN-1τm,j]T

(3)

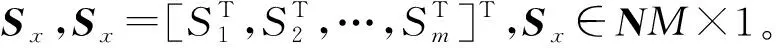
Sx=Bxwx

(4)

一般情况下，式(4)中反射系数向量wx是稀疏的，从天线测量位置M中任意选取Q1个位置，再从已经选择的测量位置中再任意选取Q2个数据。由此可以构造一个测量矩阵Ψ∈Q1Q2×NM且Q1Q2≪NM，得到的测量矩阵Ψ对Sx的投影tx可以表示为

tx=ΨSx=ΨBxwx=Φxwx

(5)

其中，Φx=ΨBx是一个Q1Q2×KL的投影矩阵。

2 多任务贝叶斯压缩感知成像算法

采用层次贝叶斯模型，通过相关任务实现信息共享，充分利用任务的统计特性，使重构结果更加精准[11-13]。因为MT-BCS的构建是基于实值信号模型，故式(5)的变化矩阵和向量为

鉴于测量噪声对结果存在影响，式(5)可改写为

t=Φw+n

(6)

n为测量噪声，故其中的元素可以近似为均值为0、方差为σ2的正态分布。故t的高斯似然函数[14]可以在参数w和σ2下表示:

(7)

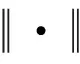
(8)

其中，α=[α1,α2,…，α2KL]T，超参数α和方差σ2是假定服从伽马分布。根据贝叶斯规则，w的后验正态分布服从多维高斯分布[15]。

(9)

其中，μ代表的是均值向量，而Σ代表的是协方差矩阵:

μ=α0ΣΦTt

(10)

Σ=(α0ΦTΦ+A)T

(11)

其中，A=diag(α1,α2,…,α2KL)，diag(·)为对角矩阵。对超参数α的求解可以进一步计算均值向量μ和协方差矩阵Σ，系数向量w可以由式(10)和式(11)解决。

3 仿真与实验结果

电磁波初始频率选取1 GHz，终端频率选取 3 GHz，频率步进点选取N=101，因此频率步进间隔为20 MHz，天线测量的位置总数M=30。假设3个目标的坐标分别为(10,40)，(20,40)，(30,40)(cm)。成像区域沿x轴从1 cm到40 cm，沿z轴从30 cm到50 cm，划分20×40均匀的空间网格。探地雷达图像分为30个任务根据不同测量孔径发射和接收天线，每个任务的回波数据来自当前测量孔径，和每个任务对应于不同的测量矩阵，将高斯白噪声的信噪比10 dB添加到频域回波数据。图3和图4为BCS的重构结果。图5和图6为MT-BCS的重构结果。

图3 测量比例为15%Fig. 3 The measurement ratio is 15%

图4 测量比例为25%Fig. 4 The measurement ratio is 25%

图5 测量比例为15%Fig. 5 The measurement ratio is 15%

图6 测量比例为25%Fig. 6 The measurement ratio is 25%

通过实验结果可以得出，该算法具有较多的噪声点和假目标。两种算法的重构目标反射系数和计算时间如表1所示。

图7为不同测量比下的重构效果。根据仿真图的结果，可以总结出:在相同的观测数据下，MT-BCS算法的重构值大大优于多次独立应用BCS算法所得到的重构值。

表1 两种算法的比较Table 1 Comparison of two algorithms

图7 比较不同测量比下的重构效果Fig. 7 Comparison of reconstruction effects under different measurement ratio.

4 结束语

介绍了MT-BCS算法，当观测数据有限的情况下，该算法对于每组任务的重构都是独立的。但是在具体的实际应用中，难免会出现存在N组观测数据是关联的，尤其是在相同条件下做的重复观测。MT-BCS算法则利用多次观测数据之间所具有的相关性特征，同时完成了多个相关信号的重构。实验结果表明，MT-BCS的重构性能良好，在较少观测数据的情况下，MT-BCS的重构性能优于BCS算法。