电机定子铁芯振动特性分析的一种解析方法

屈仁浩，蒋伟康

(上海交通大学 振动、冲击、噪声研究所，上海 200240)

电机作为电动汽车的主要噪声源之一，近年来逐渐成为电机设计中的研发热点。电机噪声的主要噪声源是定子，主要由气隙中的电磁力激发定子振动以及定子的磁致伸缩振动产生[1]。目前研究最多的是定子的电磁振动噪声，降噪设计的主要手段是准确分析定子铁芯的振动特性，优化结构参数，使其固有频率远离电磁激励力频率，避免共振。

目前电机定子铁芯的振动特性分析普遍采用有限元法[2]。Boesing等[3]使用磁固耦合有限元模型，将电磁力施加到定子齿面上，计算了定子的振动响应。邓文哲等[4]通过模态试验测定电机的模态参数，再通过有限元建立等效模型，研究了外部连接对定子固有频率的影响。韩伟等[5]建立了叠片铁芯的有限元模型，研究了叠片结构对固有频率计算的影响。有限元模型虽然计算精确，适用范围广，但计算时间长且不易修改，而在电机的减振设计和优化阶段，需要大量的模型修改与测试[6]，使用有限元法的效率会大打折扣。

解析计算方法只需要实体的简化模型，修改也十分方便[7]。使用解析模型可以快速计算出电机振动的频率范围，并给出电机噪声和结构参数的数学关系，让设计者能实时修改优化方案并快速得到反馈，从而提高设计效率。陈永校等建立了电机定子的双环解析模型计算固有频率，Islam等[8]使用环模型分析了永磁同步电机定子铁芯的振动模态，并对其施加二维电磁激励力，计算了振动响应。环模型计算虽然简单，但不能分析定子的轴向模态，因此，目前对于定子铁芯的研究，使用较多的解析模型是壳模型。Shen等[9]将定子铁芯等效为圆柱薄壳，使用解析法计算了电磁力与定子铁芯的振动响应；邱家俊等[10]建立了水轮发电机定子系统的双薄壳模型，并采用梁函数来表达不同的边界求解定子系统的固有频率。壳模型的计算虽然已经成熟，但由于忽略了定子齿部的影响，误差较大。Singal等[11]采用壳模型计算了短定子铁芯的固有频率，经试验验证：前7阶固有频率误差为15%。

为了能够在电机初步设计阶段，快速便捷地预测定子振动噪声特性，或进行低噪声电机定子的优化设计，本文建立了一种能快速准确计算定子铁芯振动特性的解析模型，提出了一种可以考虑定子齿变形的厚壳-梁耦合简化模型；推导了耦合模型的能量变分方程，使用Rayleigh-Ritz法计算了定子铁芯的固有频率与振型。与有限元方法进行对比验证，所提解析算法计算准确，且无需建模与网格划分，效率更高。仿真结果还表明，定子齿对铁芯振动特性的影响不能忽略。

1 定子铁芯的简化模型

由于解析模型只适用于简单的板、壳或梁结构，因此首先需要对定子模型进行简化。本文提出了一种厚壳-梁耦合简化模型。去除定子表面的凹槽与齿上的圆角等细节，定子铁芯的简化模型与相应坐标系如图1所示。由于定子轭厚与半径比值较大，使用薄壳理论建模会有较大的误差，厚壳模型更加合理。轭上分布着若干齿，定子齿采用计入扭转变形的梁模型进行建模，以表达齿的弯曲和扭转刚度。由于齿宽度远小于定子周长，因此可以假设厚壳模型和梁模型间为线接触[12]，接触线为P，本文建立的解析方法均基于此简化模型。

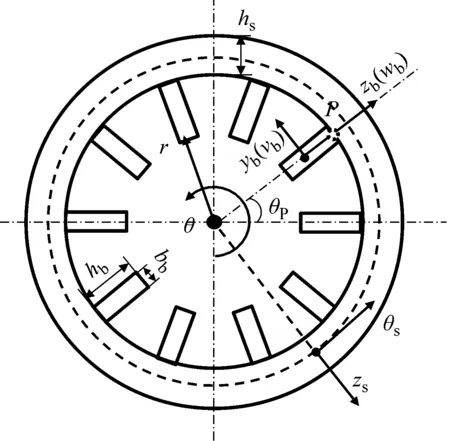
图1 定子铁芯简化模型与坐标系

2 定子铁芯的变形方程

2.1 定子轭的变形方程

对图1所示的圆柱厚壳，曲线坐标1,2,3分别对应壳中面坐标系下的xs,θs,zs方向，该坐标系下圆柱厚壳的应变表达式为：

(1)

式中：R是壳中面半径。在式(1)的基础上，引入零剪切应变等假设便可得到薄壳的方程，若不对式(1)进行假设，则是适用于厚壳的一般壳体力学方程。

壳体内的应力分布通过材料刚度矩阵与应变表达，由于定子是叠片结构，轴向与周向、径向的机械特性不同，因此应使用正交各相异性结构的本构关系：

(2a)

(2b)

式中:σi,i=xs,θs,zs表示正应力，τij,i,j=xs,θs,zs表示剪切应力，Cij是各相正交异性材料刚度矩阵中的元素，各项的表达为：

Cii=ηEi(1-νjkνkj),

Cij=ηEj(νij+νikνkj),

(3)

采用Mindlin板中的一阶剪切变形理论，如图2所示，变形后的壳面法线保持直线但不再垂直于壳面[13]，而会产生转角φxs。假设壳中面轴向、切向和径向的变形分别为us,vs,ws，则厚壳中任意一点的变形可以表示为：

图2 一阶剪切变形理论

uxs=us(xs,θs,t)+zs·φxs(xs,θs,t)，

uθs=vs(xs,θs,t)+zs·φθs(xs,θs,t)，

uzs=ws(xs,θs,t)+zs·φzs(xs,θs,t)

(4)

式中：t表示时间项，φxs,φθs分别表示厚壳截面变形后在xszs面和θszs面内的斜率，即变形时的转角，而φzs则表示厚壳在zs方向变形的变化率。

2.2 定子齿的变形方程

为了能计入定子齿的刚度与变形，定子齿必须单独建模。由于电机中的电磁力主要是径向和切向分量[14]，因此本文主要研究定子齿在径向的弯曲变形以及绕轴向扭转变形。采用欧拉梁理论进行建模，同时计入梁的扭转变形。在图1所示的直角坐标系xb,yb,zb下，齿的变形方程为：

uyb=vb+zb·φyb，

uzb=wb

(5)

式中:ui,i=xb,yb,zb表示梁上任意一点沿xb,yb,zb三个方向的变形分量；而ub,vb,wb则分别表示梁轴线的变形分量，φyb表示绕xb轴的扭转角。根据弹性力学理论，梁的弯曲应变εxb与扭转应变εφb分别为：

(6)

3 定子铁芯的振动方程

3.1 定子轭和齿的能量

根据结构力学的能量理论，圆柱壳在变形时产生的弹性势能为[15]：

Πs=∭Vπs(uxs,uθs,uzs)(R+zs)dzsdθsdxs,

(7)

式中，πs是单位体积的应变能。

将式(1)～(4)代入式(7),可以得壳体应变能关于中面变形表达式式(8)。

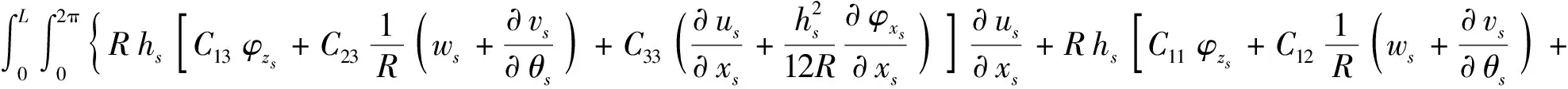
(8)

为将3维问题简化为2维，式(8)已在厚度方向zs上积分，hs表示壳体的厚度，coi,i=1,2,3是在厚度方向积分时产生的系数项，分别为：

(9)

圆柱厚壳变形在体积Vs上产生的总动能为式(10)：

(10)

式中：同样是对厚度方向积分后的结果，ρs表示定子材料的密度，点号表示对时间求导。

同理，根据欧拉理论，可以写出定子齿的弹性势能Πb与动能Tb的表达式：

(11)

式中：Eb,Gb分别表示梁的拉伸和剪切模量，Vb表示梁的体积。

3.2 定子轭与齿耦合

由于定子轭与齿能量的推导分别在柱坐标系xs,θs,zs与直角坐标系xb,yb,zb下，为了研究定子整体的能量，必须统一坐标系。电机振动时定子的辐射噪声主要是圆柱面振动产生，因此，可将图1中圆柱坐标系x,θ,r作为整体坐标系，将定子铁芯的变形在整体坐标系下进行表达。

由图1可知，整体坐标系的x坐标与xs,xb均相同，表示定子轴向；θ坐标与θs相同，表示定子周向。图1中定子轭和齿的耦合直线P的局部坐标分别为θs=θP,zs=-hs/2；和zb=hb/2,yb=0。在此直线P上，由位移连续条件，梁和壳体的位移相等，且绕x轴的扭转角相同。耦合条件可以表达为：

(12)

式中：上标b,s分别表示梁和壳的局部坐标系，u表示直线变形，φ表示扭转变形。将式(4)、式(5)以及P的坐标代入式(12)，可以推导出定子齿变形与厚壳变形的关系表达式为：

(13)

将式(13)代入式(11)，可以得到定子齿在整体柱坐标系x,θ,r下的的弹性势能和动能为：

(14)

(15)

式中:Jb表示矩形截面梁的扭转刚度，需根据梁截面的形状进行近似计算[13]。N表示定子齿的数目，Iyy是定子齿轴向截面关于yb轴的转动惯量。

将式(8)、(10)分别与式(14)式(15)相加，可以得到定子整体的拉格朗日能量泛函为：

L(us,vs,ws,φxs,φθs,φzs)=Ts+Tb-(Πs+Πb)

(16)

3.3 定子铁芯振动特性求解

根据哈密顿原理，弹性体的运动变形必使能量泛函的积分作用量取得极小值，即：

(17)

在力学中，能量变分方程的求解，可以使用Rayleigh-Ritz法，首先假设出中面在两端简支约束下的位移试探函数：

(18)

式中：x,θ表示图1中的总体坐标系，中i表示虚数符号，αm=m·π/L表示x方向的半波数，n表示θ方向的波数，ω表示振动的频率。

将式(18)代入式(17)中，利用振型函数的正交性，可以得到(m,n)阶振动的能量泛函为：

(19)

以Umn,Vmn,Wmn,Ψmn,Φmn,Θmn作为广义坐标，对能量泛函Lmn进行广义变分处理，最终可以得到定子结构的广义刚度矩阵Kmn和广义质量矩阵Mmn：

(20)

式中：Dmn即为广义位移向量[Us,Vs,Ws,Ψs,Φs,Xs]′，Kmn和Mmn分别为：

(21a)

(21b)

4 数值计算与仿真验证

为了验证解析方法的准确性，使用解析法与有限元方法计算一6相8极表贴式永磁同步电机定子铁芯的固有频率，在去除圆角，凹槽等细节之后，简化的定子模型尺寸如表1所示。表1可知，定子轭厚度与半径比值超过1/6，属于厚圆柱壳。由于定子的叠片结构，定子轴向和横向的机械性能存在差异，因此材料属性等效为横观各向同性，即轴向参数与径向、周向不同。根据邓文哲等对叠片结构的定子各向异性等效弹性模量试验测定，对周向、径向弹性模量有Eθs,Ezs=0.85E，轴向为Exs=E，而对于剪切模量则有Gzsθs=0.85G，Gxsθs,Gxszs=0.14G。其中E,G分别为各向同性硅钢片的杨氏模量和剪切模量。

表1 数值与仿真验证定子参数

有限元模型如图3所示。图3(a)是定子铁芯模型，定子轭采用壳单元划分，定子齿采用梁单元划分，共计5 982个节点，11 550个单元，壳两端施加简支约束。此外，为了证明定子齿变形对固有频率的影响，同时建立了一个质量等效的厚壳有限元模型，如图3(b)所示，壳的尺寸为定子轭的尺寸，将齿的质量增加到壳体后，等壳厚壳的密度变为10 741 kg/m3，其他参数与条件均保持不变。

(a)定子铁芯模型

表2中m表示定子x轴向的模态阶数，n表示定子θ周向的模态阶数，轴向模态的差异可以从n=0的模态中看出。相对误差标准值均基于定子铁芯有限元计算结果。由图4可知，所研究定子的前6阶固有频率主要集中在2～7 kHz内，若不考虑齿变形，仅做质量等效，则计算的0节圆(m=1)的低阶模态的固有频率误差为12%以内，单节圆(m=2)低阶模态的误差高达28%，说明定子齿的变形不能忽略，间接证明了本文研究的必要性。本文所提解析方法可以准确计算出定子铁芯对应振型的固有频率，0节圆各阶模态固有频率的相对误差小于3%，单节圆各阶模态误差小于5%，满足工程计算精度，证明了解析方法的正确性。该解析方法只需输入结构的外形尺寸，计算无需网格划分，因此与有限元相比更为简单，同时，参数的修改也十分容易，无需重划网格。

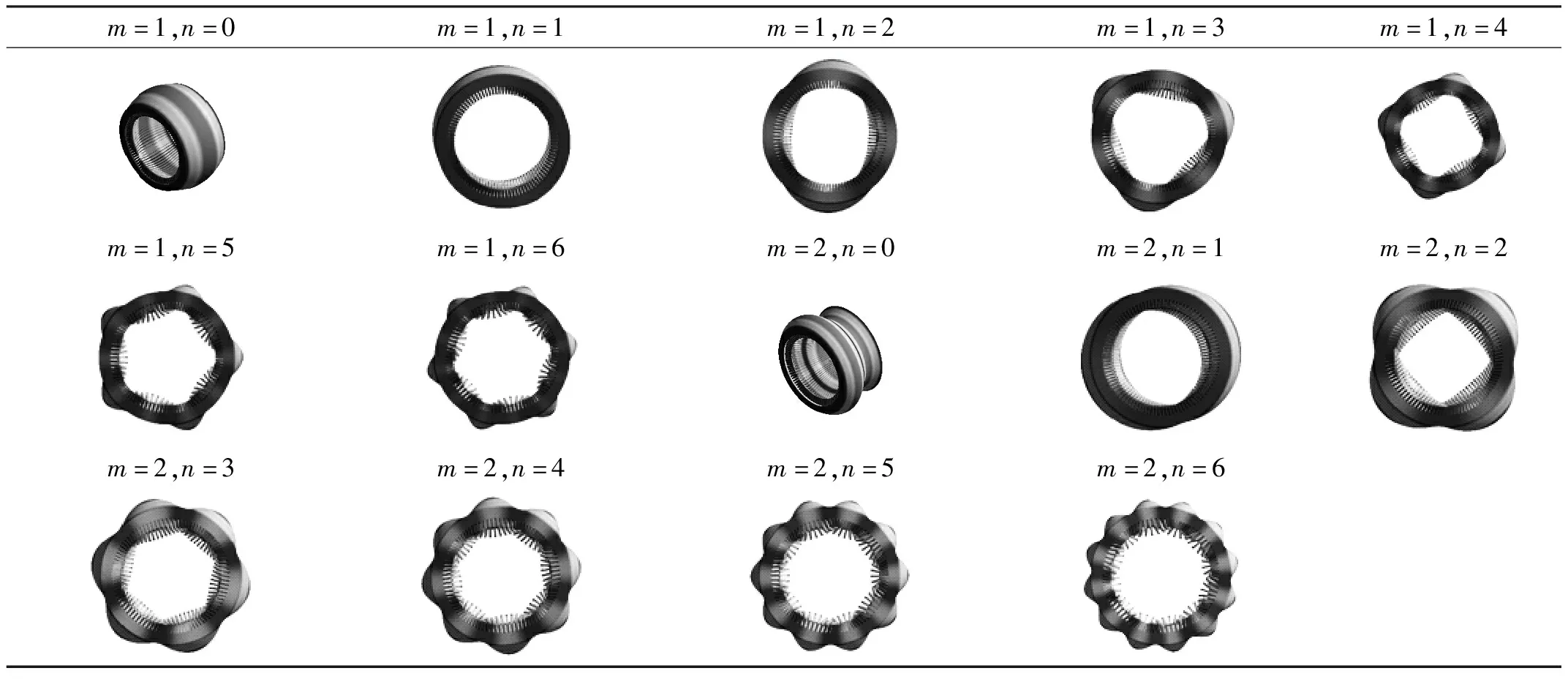
表2 定子铁芯模态振型计算结果

(a)定子铁芯的固有频率比较

5 结 论

本文研究了一种解析方法快速计算电机定子铁芯的振动特性。提出了一种可考虑定子齿变形的厚壳-梁耦合简化模型，推导了耦合结构的能量变分方程，并使用Rayleigh-Ritz法求解了模态振型和固有频率。经验证，本文提出的解析方法计算得到的各阶模态的固有频率，与有限元仿真结果的相对误差在5%以内，满足工程计算的精度要求；若不考虑定子齿变形，低阶固有频率误差为12%，说明定子齿的影响不能忽略；所提解析方法省去了有限元计算时的建模与网格划分过程，提高了计算效率，可用于需快速预测定子振动噪声特性的电机初步设计阶段。