多尺寸纱筒柔性落纱机械手设计及其优化

张 凡，管声启

(西安工程大学 机电工程学院，陕西 西安 710048)

基于市场对服饰花色的需求，混色拼接纱线逐渐成为市场主要的纺纱方式之一，已经成功应用于棉纤纺织领域。自动落纱作为混色纱线拼接的重要环节，其主要功能是代替人工实现纱筒的自动落纱，并将新的空纱筒夹持到纱锭上[1]。

由于空纱筒和满纱纱筒尺寸大小各异，其传统落纱纱筒直径范围在20～80 mm之间，落纱时机械手或抓取空纱筒中间部位，或为避免损伤纱线而抓取满纱纱筒末极梢无纱线处，其尺寸差异波动性较大，因此很难完全实现自动化多尺寸纱筒落纱[2-3]。近年来，针对纱筒自动落纱问题，国内外相关领域学者开展了广泛而深入的研究，并取得了一定成果。传统落纱多以连杆、旋搓、气动柔性抓取或多组机械手协同完成落纱任务。旋搓机械手利用浮动连接杆的摆动自动适应锭子的安装误差，以平行四边形机构实现纱筒夹紧力，可稳定夹持直径18 mm纱筒，夹取力可达1.4 N，但其只适用于单一直径纱筒落纱[4]。柔性气动抓取执行器，其结合实验和理论分析设计的基于纺织品的整合机械手，以辅助纺织行业中柔性物体及圆形上料抓取，充分利用了高伸缩性纺织品的各向异性特性，抓取效果良好，抓取成功率较高，但其高成本性及结构复杂性决定了此机械手难以大范围使用[5]；多组机械手协同连续落纱机器人，以多组两指机械手组成自动落纱小车为环锭细纱机进行自动落纱，可完成对单一66 mm直径纱筒的自动落纱[6-7]。

上述传统落纱机械手在一定程度上均可完成落纱抓取任务，但其主要针对单一尺寸直径纱筒，或者较为规则的物体进行抓取，在多尺寸纱筒的抓取问题上(尤其是纱筒存在着一定锥度)，难以满足纱筒多尺寸抓取差异性波动的需要，抓取失稳，降低抓取率，且其多体积较大。

针对以上问题，本文采用仿生学手指结构及抓取原理，设计优化一种自动落纱机械手实现多尺寸落纱。以仿生学理念建立机械手模型，以新型传动方式进行动力传递，完成柔性设计；以三维多向量粒子群算法进行多尺寸机械手优化，使其适应多尺寸纱筒柔性抓取，提高落纱稳定性，减小机械手尺寸,并通过有限元仿真试验对比验证可行性。

1 落纱机械手结构模型构建

1.1 机械手落纱抓取过程分析

落纱机械手作为自动落纱环节的重要部件，其任务是，抓取空纱筒固定于纱架纱锭上，待混色纱线缠满纱筒时，机械手将满纱纱筒(直径为50～80 mm)从纱锭上夹取落下以供新的纱筒持续作业[8]。在纱线拼接过程中，当一个锭位完成拼接后，机械手接受命令开始移动至目标位置处，进行落纱抓取，在抓紧纱筒后移至纱框处，进行放纱，而后根据坐标信息，抓取空纱筒(直径为30～50 mm)，将空纱筒移至上一落纱纱锭处，缓慢松开纱管，继续落纱任务，如此循环该流程[9-10],落纱过程如图1所示。

图1 落纱过程分析

对于纱筒的抓取，尤其需要注意抓取过程的稳定性。传统刚性落纱机械手在进行落纱时，纱筒和锭子之间水平方向不允许相互碰触及运动突变，避免纱筒刚性碰撞，损坏纱筒[11]，机械手的设计需要实现多尺寸纱筒稳定、柔性的落纱抓取。

1.2 落纱机械手结构建模

在混色纱线拼接落纱过程中，落纱机械手远指节带动其余指节协同弯曲，机械手以球形空间逐渐收拢，形成托举抓取位姿；在接触纱筒时，其多指互相配合及约束，达到锁死状态，完成抓取。

传统机械手采用绳索、肌腱传动大大减小其整体尺寸，满足了纱线拼接空间狭窄要求，但其也存在明显的缺点。由于绳索、肌腱弹性模量较大、线弹性高问题，在面对带有2°～5°锥度的纱筒落纱时，随着拉力不断增大，其指尖因绳索弹性逐渐回弹，夹紧的物体进而发生松弛，导致落纱失败。

因此，在采用绳索作为传动方式时必须解决其震颤回弹问题。本文采用绳索传动和连杆结合的新型传动方式，以绳索拉力为主传动，以连杆为张紧装置，在传动绳索拉动指节转动时，张紧连杆由关节心轴同时带动，在整个抓取过程中，张紧连杆保持绷紧状态，限制指节震颤回弹，起到张紧作用，避免抓取失败。机械手指原理如图2所示，图中θ1、θ2、θ3分别为远、中、近指节极限转角。

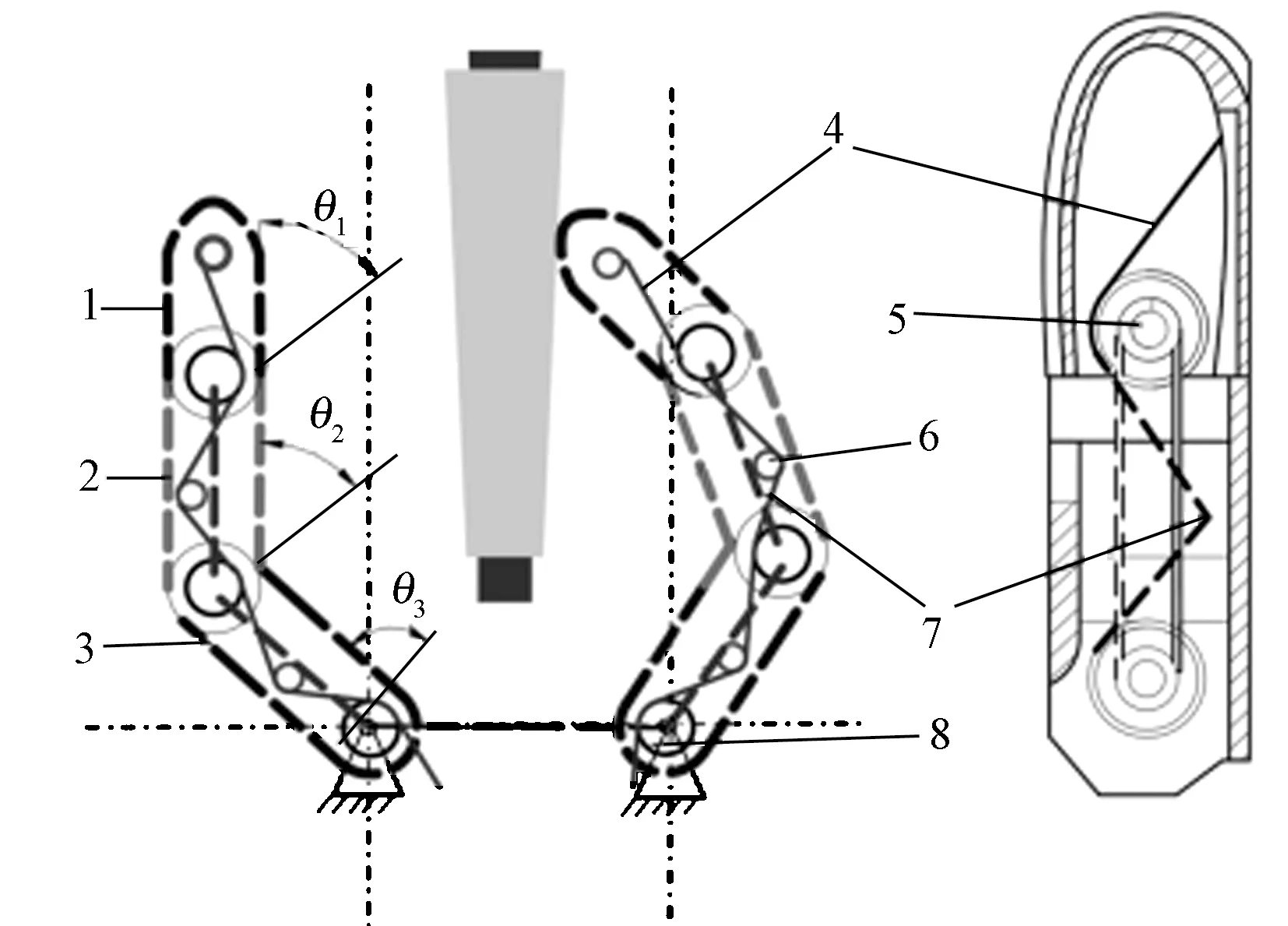
1—远指节；2—中指节；3—近指节；4—绳索；5—关节滑轮；6—导向轮；7—张紧杆；8—底盘固定处。图2 机械手指原理

绳索从远指节处向下拉伸，直至固定底盘处。从固定底盘至电机滑轮处，绳索通过1、2级导向轮进行导向，以减小空间体积。1、2级导向轮分别固定至手指垂直下方，其与近指节相错10°进行装配，底盘布绳装配如图3所示。

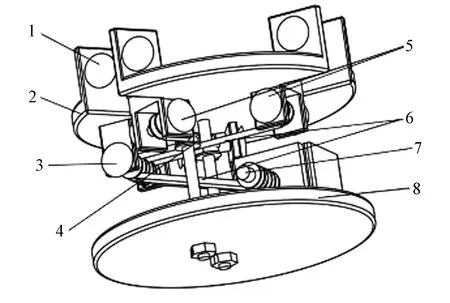
1—指节固定处；2—上底盘；3—固定销钉；4—2级滑轮；5—1级滑轮；6—绳索；7—电机轴；8—下底盘。图3 底盘布绳装配

人体手掌具有5指结构，可适应多种形状物体灵活抓取。但对于落纱抓取，其形状相同，尺寸相差，采用5指结构抓取过于复杂、体积较大。且由于人体手指最常用的为拇指、食指、中指，大多数抓取行为以此3指完成，因此机械手采用3指结构，机械手整体结构如图4所示。

图4 机械手整体结构

混色纱线拼接落纱机械手3根手指以120°均匀分布，抓握时形成径向力及向上托举力，完成稳定抓取,同时减小体积。

1.3 落纱机械手结构柔性抓取设计

为避免传统刚性机械手在抓取纱筒时因夹紧力作用损伤纱线，造成残次品纱筒的问题。以刚柔耦合形式进行机械手指尖的柔性设计。以仿生学为原理，机械手以刚性材料为内部骨质支撑，以柔性材料80 A硬度TPU为整体指节材料层。区别于传统在刚性部件外覆盖一层柔性材料实现的有限变形，本机械手远指节整体以纯柔性材料成型，内部指骨承担力传递功能。抓取时，内部指骨通过弧形棱角支撑持续转动，在接触物体时发生自适应形变，形成凹陷变形后被指骨阻隔，保证所需夹持力。

2 落纱机械手结构模型参数优化

在建立机械手结构模型的基础上，为了实现机械手适应多种尺寸纱筒柔性抓取功能，需要对其参数进行设计优化。

2.1 优化变量选取

机械手抓取纱筒如图5所示，L1、L2、L3分别为远、中、近指节长度,mm；θ1、θ2、θ3分别为关节1、关节2、关节3极限转角,rad；R为机械手初始位置最大直径,mm。在指节弯曲运动过程中，指节长度对多尺寸纱筒抓取工作范围及抓取精度有较大影响，且指节所能转过的极限夹角的不同将形成完全不同的抓取效果。因此选优化变量为L1、L2、L3、θ1、θ2、θ3。

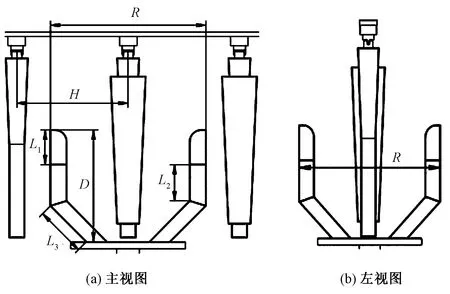
图5 机械手运动轨迹图

2.2 优化模型建立

对于机械手优化设计，尽可能减小构件的尺寸以及质量。以机械手末端位姿及关节极限转角为出发点，将纱筒尺寸分割为多个短向量范围，因此，优化算法数学模型为：

F=F(X);X∈Rm；

|X|≤[ximin∶ximax]

(1)

式中：F(X)为X目标函数；Rm为m维实集；ximax、ximin分别为短向量上下限，i=1，2，3。

2.2.1 建立参数目标函数

在参数选定的基础上，建立多尺寸范围向量与多参数之间的三维模型。机械手的弯曲运动轨迹如图6所示，运动轨迹为圆弧状，其工作转动总面积公式为：

(2)

式中：S为机械手总转动面积，mm2；S1、S2、S3、为远、中、近指节转动面积，mm2；φ1、φ2、φ3分别为远、中、近指节转动角度，rad。

将指节转角参数代入转动面积公式可得目标函数1为：

(3)

式中：X1、X2、X3为长度优化变量，mm；X4、X5、X6为极限夹角优化变量，rad。

各指节尺寸参数也应该在各自约束情况下遵守最优原则，其3个指节抓取范围之和以适应度值表示，且应达到精确。因此，目标函数2为：

F2(X)=X1+X2+X3；

(4)

F(X)=K1minF1(X)+K2minF2(X)

(5)

式中：K1、K2为加权系数，K1+K2=1。

图6 机械手运动轨迹面积图

2.2.2 确定目标函数约束条件

为保证纱筒的柔性抓取，机械手末端位姿的3个指节在分方向投影应大于最小可包络抓取纱筒的直径，而小于最大可抓取物体直径。纱筒常用尺寸如下，空纱筒直径为30～50 mm，长度L1为175～190 mm；纱筒直径为50～80 mm，长度L2为135～150 mm；纱架锭距为150～180 mm。因此有纱筒直径增量为30～80 mm，且将其离散化，分成多参数，短向量。其约束为：

[50∶80]≥R-[|sin(X6)|X3+|sin(X6+X5)|X2+

|sin(X5+X4+X6)|X1]≥[30∶50]

(6)

式中：R为机械手最大直径，mm。

由常用纱架锭距数据可得边界条件为：

(7)

式中：H为纱架锭距，mm；φmax为纱筒最大直径，mm；D为机械手末端投影垂直高度，mm。

2.3 优化模型计算

利用工具MatLab编写粒子群函数程序进行三维二次寻优，找到最优参数的同时确保纱筒直径可被稳定抓取，其结果如表1所示。

表1 机械手长度优化参数

3 落纱机械手仿真实验验证

为进一步验证新型机械手落纱可行性，采用有限元软件进行仿真分析。传统仿真或以仿真软件ADAMS进行单独动力学仿真，或以仿真软件ABAQUS模拟材料相互作用性能，其分别只能仿真一部分，不能充分反应运动变形情况[12]。现以ADAMS及ABAQUS进行联合仿真，以ADAMS作为前处理工具，ABAQUS作为后处理工具，进行结果对比分析。

3.1 机械手落纱过程仿真验证

3.1.1 实验条件确定

为统一实验标准，仿真实验均以电机General Motions驱动绳索，其转动速度呈线性匀速，机械手载荷以转动电机形式实现，其转速设置为0.3 rad/s，仿真时间为5 s；以新型弹性材料TPU建立本构模型，采用多项式Ogden赋予材料；以30～80 mm直径纱筒为抓取对象，对设计机械手进行抓取仿真对比分析。

3.1.2 落纱机械手实验方案设定

将三维模型在ABAQUS中装配。为验证机械手对多尺寸纱筒柔性抓取可行性，对30～80 mm直径纱筒进行落纱对比分析。对新型材料TPU进行双轴、等轴、平面拉伸实验得到应力、应变参数。其绳轮设定使用约束SLIP RINGS动滑轮进行约束。由于采用动力显示分析，因此网格划分需设为线性网格EXPLICITC3D8R类型。绳索固定于远指节指背，在绳索另一端加载负载进行拉伸，时间设定为5 s。仿真过程如图7所示。

图7 仿真过程位姿

整个实验过程分为3步，图7(a)为第1步，施加载荷，绳轮绷紧，手指开始运动；图7(b)为第2步，载荷接触建立完成，持续转动；图7(c)为开始接触纱筒，减速直至完全夹紧纱筒。

3.2 落纱仿真实验结果分析

由于抓取过程中，机械手运动稳定性直接决定抓取成功率，因此利用动力显式方法分析各关节运动拟合曲线，机械手仿真后处理图如图8所示。

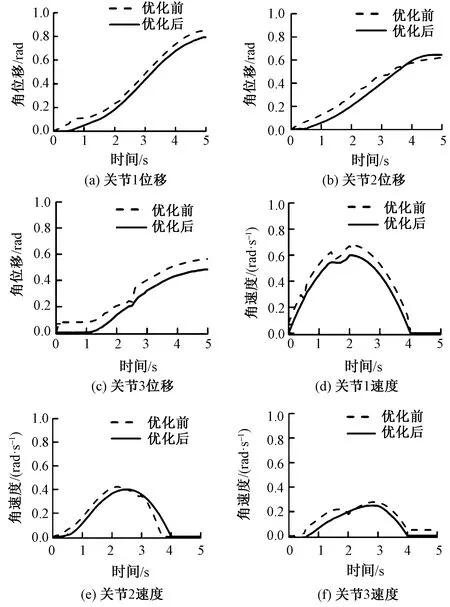
图8 机械手仿真后处理图

分析图8可得，在抓取纱筒时，优化过后的各关节角位移幅值均减小0.1～0.2 rad，达到了优化参数精简尺寸的要求。且其图像较为光滑，减少了突变点，无回弹，实现了不同尺寸直径纱筒的平稳抓取。由于影响关节转动稳定性另一重要指标为角速度变化，因此对三关节角速度数据进行详细分析对比，关节角速度如表2所示。

表2中“↓”表示下降，优化过后除关节2在2.5 s时上升外，其1、2、3关节峰值均分别下降0.084 、0.073 、0.027 mm，百分比下降9%～13%，均值及均方根百分比下降11%～29%。由于均值及均方根数值代表机械手空间运动状态的稳定性，其值越小，数据越稳定，因此可验证机械手在优化过后的抓取稳定性更高，波动越小，多尺寸纱筒落纱抓取过程得到稳定性改善。

表2 关节角速度分析

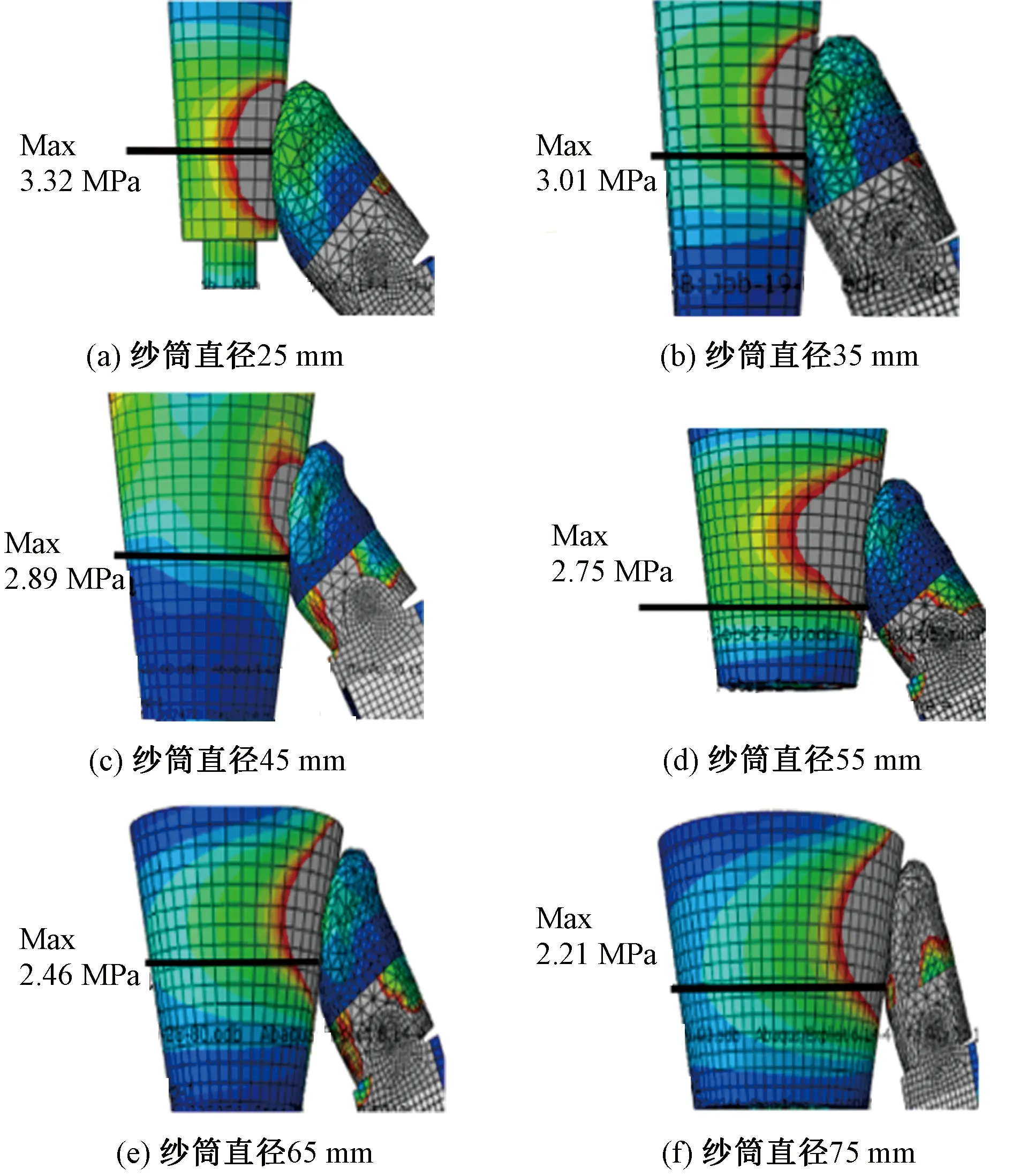
图9 落纱抓取自适应形变

在运动稳定性得到改善验证后，进一步对不同尺寸纱筒落纱抓取情况进行验证分析。图9(a)～(f)分别对应直径为30～80 mm的纱筒落纱抓取截面图，3根手指对称布置，其受力相同，只列举其中一根手指接触进行分析。由实验可得其远指节转动角度为：0.49～0.84 rad之间，其值小于各关节计算所得极限夹角1.54～2.09 rad，因此符合落纱抓取末端位姿要求；远指节横截凹面接触长度为：16.21～22.12 mm，其接触长度尺寸均达到纱筒直径1/3，可实现包络式的柔性落纱抓取；其接触应力为：2.12～3.32 MPa，而纱筒最小许用应力为25 MPa，其落纱实验接触强度安全系数远大于1，由此可得机械手可安全无损伤地完成多尺寸纱筒柔性抓取。

从仿真参数可得机械手在抓取时具有较好的柔性包络变形能力，且在形成凹陷包络的同时保持了足够的夹取力，实现了对不规则、有锥度、多尺寸纱筒的稳定自适应落纱抓取。

4 结 论

通过对人体手指位姿研究分析，以落纱纱筒尺寸及作业环境为依据，设计了新型多尺寸抓取落纱机械手。以多维短向量标准建立优化函数模型，运用三维多向量优化方法得到了机械手尺寸优化参数，在保证多尺寸纱筒的适应性抓取落纱的同时，实现了机械手轻巧化设计，达到灵巧化抓取；最后，在有限元仿真计算中，其数据对比显示，与传统单一尺寸落纱机械手相比，新型机械手可稳定实现30～80 mm多尺寸纱筒柔性落纱，为以后的柔性抓取控制系统建立奠定了良好的基础。