基于贝叶斯估计的多探测器火警判定方法研究*

刘 罡，黄丽达，袁宏永，于淼淼

(清华大学 工程物理系 公共安全研究院,北京 100084)

0 引言

火灾探测器是消防火灾自动报警系统中的重要装备。目前国内外主流的探测模式是单点报警，国内超过90%的探测器属于感烟探测器[1]，安装容量达30亿只以上。然而受探测器质量等因素影响，火灾误报现象较为严重。据统计，发达国家例如美国的探测器误报率为0.17次/(只·a)，瑞士、日本、德国分别为0.04，0.06，0.01次/(只·a)，而我国的探测器误报率远高于发达国家，广州为0.45次/(只·a)[2]，清华大学公共安全研究院测试全国约为0.66次/(只·a)。

为提高火灾识别的准确性，国内外学者进行了多方面的研究。一些学者试图利用新方法解决现有问题，如Carter[3]提出1种利用红外图像识别火焰的方法；Zhang等[4]利用可调激光二极管吸收光谱(TDLAS)检测CO气体识别森林早期火灾。这些新方法的成本较高，短时间内难以取代感烟探测器。一些学者考虑利用多种火灾参数提高识别准确率，如Liu等[5]提出1种基于数字信号处理的火灾温度特征与光电信号的复合识别算法；Homeag等[6]基于真实尺度火灾实验数据，使用火灾的烟、温、气特征，提出1种基于人类经验的模糊专家系统火灾检测算法；Ding等[7]利用D-S证据理论提出1种检测光、烟、温度、气体、湿度的多传感器信息融合算法。这部分研究利用感烟、感温、火焰成像、燃烧产物等多种类型的探测器对火灾进行复合探测，以覆盖各火灾类型与火灾发展阶段，但由于部分方法的机理限制，受应用场景限制较多，短期内同样难以实现大规模布置。近年来随着视频监控的增多，部分学者研究基于图像处理与人工智能的火灾识别方式，Hashemzadeh等[8]提出1种基于K-medoids色彩模型的帝国竞争算法(ICA)火灾探测方法；Muhammad等[9]提出1种卷积神经网络SqueezeNet方法的火灾识别算法；Frizzi等[10]提出1种轻量级的CNN算法，用于快速识别视频中是否起火。这类方法可以充分利用视频监控设备实现精准识别与定位，但仅适用于公共场所，无法满足家庭、酒店、办公室等大量视频监控无法覆盖的私密空间的需求。目前感烟探测器布置比例最高，如何提高现有感烟探测器的报警准确性具有重大的现实意义。然而现有的研究很少有针对感烟探测器进行探测算法优化以提高火灾识别精准度的方法。

本文考虑使用多个感烟探测器耦合检测，首先基于理论计算说明多探测器系统对减小误报率的作用，然后提出基于贝叶斯估计理论的多探测器火警判定方法，并通过对典型火灾场景的模拟验证该方法的可行性与有效性。

1 研究方法

1.1 多探测器耦合检测方法

火灾烟气分布情况会受到建筑空间结构的影响，本文将反映建筑空间中烟气蔓延规律的最小空间单元定义为“建筑结构微元”，如平顶房间、高大空间、走廊、各类竖井等。

为解决单个感烟探测器的高误报率问题，本文针对某一火灾事件，将建筑结构微元中多个感烟探测器的报警时间进行耦合分析。假设建筑结构微元中有n个探测器可以用于报警，模型报警需要r个探测器正常工作。利用探测器的报警时间t1,…,tn，计算相邻报警时间的时间间隔Δti=ti+1-ti，将火灾发生时任意2个探测器的最长报警时间间隔记为最不利报警时间间隔Δtmax，则建筑结构微元内多探测器耦合火灾报警模型误报的概率如式(1)所示：

(1)

假设误报的发生是独立事件，由于Δtmax远小于探测器寿命，则单个探测器的误报次数服从泊松分布[11]。实际情况中，通过对误报的统计得到单个探测器在1 a时间T内的平均误报次数λ为0.66，从而计算得到q如式(2)所示：

(2)

式中：Δtmax为最不利报警时间间隔，s；T为1 a时间长度，取3.155 7×107s；λ为年均误报次数，取0.66。

根据Pw计算得到建筑结构微元内多探测器耦合的火灾报警模型的年均误报次数如式(3)所示：

(3)

式中：Λ为使用火灾报警模型的年均误报次数。

考虑建筑结构微元中的探测器数量n以及火警模型判定所需的探测器数量r，本文绘制不同情况下火灾报警模型的年均误报次数，如图1所示。由图1可知，多探测器耦合模型中每增加1个探测器，理论上误报率约降低4个数量级。

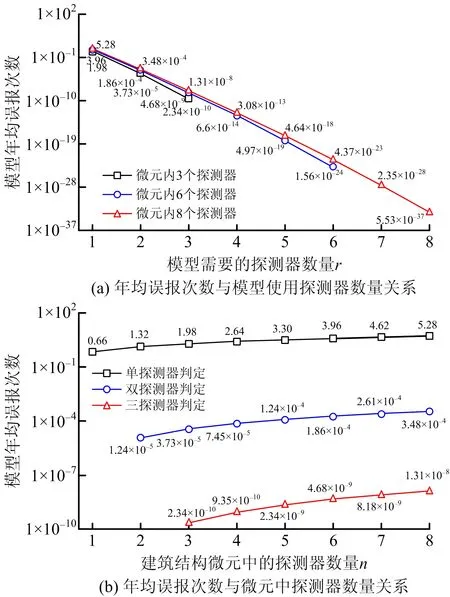
图1 多探测器耦合模型的年均误报次数Fig.1 Average annual frequency of false alarms by multi-detector coupling model

1.2 基于贝叶斯估计的火警真实度计算模型

贝叶斯估计是基于贝叶斯理论对概率分布参数进行估计的方法，利用观测得到的信息与参数的先验概率分布得到其后验概率分布，从而实现该参数的估计。本文使用贝叶斯估计方法，利用各次火警时间间隔观测值Δt′估计火源位置θ(x,y)的分布，进而计算得到用于判定火警事件的火警真实度E，并利用多次观测结果迭代计算，提升模型精度与可靠性。

考虑每1次火源位置分布更新的过程。当2个探测器位置固定时，火源位置与理论报警时间间隔Δt(可由经验公式或模拟仿真得到)存在确定关系，假设其为Δt=T(θ)。

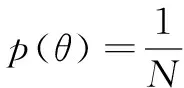
(4)

式中：fΔt(j)为报警时间间隔的先验分布；I为矩形窗函数；δtj-1与δtj为区间边缘，s；θ为火源位置；p(θ)为火源位置先验分布；T(θ)为时间间隔与火源位置的理论关系函数；M为时间间隔区间数量；j为区间的序号。

考虑贝叶斯估计公式，将其写为理论报警时间间隔Δt与观测Δt′的关联形式，如式(5)所示：

(5)

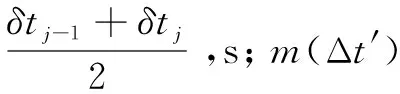
边缘似然率的计算方法如式(6)所示：

(6)

本文使用g(Δt′|Δt)描述实际测量和模型计算之间的误差分布，具体包括模型的建模误差，火灾过程的随机性和不确定性，以及探测器的测量噪声等。对2个探测器而言，假设每个探测器的测量误差与模型的预测误差是独立的，探测器误差之间具有独立性，假设其服从概率密度分布h(t)，则得到似然函数如式(7)所示：

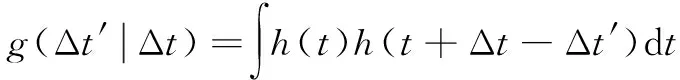
(7)

式中：h(t)为单探测器报警时间误差的概率密度分布函数。

对探测器误差的概率分布而言，常见的似然函数包括正态分布、对数正态分布、t分布、柯西分布以及对数柯西分布[14]。

将算法用于火灾监测时，可以根据实际情况选取合适的概率分布。其中，对于最为常见的正态分布，可计算似然函数，如式(8)所示：

(8)

式中：σ为单探测器测量标准差，s。

同理，可利用火源位置与理论报警时间间隔之间的确定关系，由报警时间间隔的后验分布计算得到火源位置的后验分布，如式(9)～(10)所示：

(9)

(10)

式中：p(θ|Δt′)为火源位置的后验分布；p(θ|j)为第j个时间间隔区间下火源处于位置θ的概率。

由于火源位置信息不随观测变量的变化而变化，可以将每次观测时火源位置的后验概率分布作为下一次观测时的先验概率分布。进而依次得到第i次观测时的各概率分布关系，如式(11)～(14)所示：

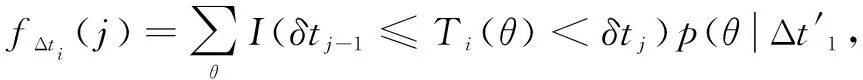
(11)

(12)

(13)

(14)

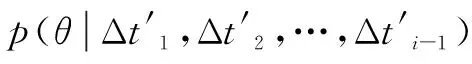
由于火警真实与否的判断过程是无法通过位置分布直接得到的，因此本文针对火灾是否发生的问题，定义火警真实度E，以该值的大小反映火源位置分布的合理性与有效性，进而反映火警的真实性，从而实现火灾真警的判定，第i次观测后的火警真实度计算方法如式(15)所示：

(15)

式中：Ei为第i次观测后的火警真实度，取值范围为0到1；σx,i为i次观测后，基于火源位置后验概率分布在x轴向上的边缘分布标准差；σy,i为i次观测后火源位置分布在y轴向上的边缘分布标准差；σx,unif为均匀分布在x轴向上的边缘分布标准差；σy,unif为均匀分布在y轴向上的边缘分布标准差。

2 实验设计

为验证本文中提出的基于贝叶斯估计的火警判定方法的有效性，获取报警时间计算得到的位置分布的特点以及火警真实度E的变化趋势，选取3个典型建筑结构微元开展研究：狭长走廊、腔室和楼梯井。其中狭长走廊火灾场景用于说明探测器线性布置时对火源情况的识别效果；腔室火灾场景用于说明探测器有平面结构时对火源情况的识别效果；楼梯井火灾场景用于说明探测器与烟气蔓延沿高度方向分布时的火源情况识别效果。

本文使用FDS模拟仿真数据作为报警时间的观测值，为引入探测器误差，使用报警时间的经验公式作为理论值[15](该公式的系数根据实验和仿真数据修正)，并假设探测器误差服从正态分布。针对狭长走廊火灾、腔室火灾、楼梯井火灾，其报警时间公式，依次如式(16)～(18)所示：

(16)

(17)

t=0.482z2.219

(18)

式中：t为理论得到的报警时间，s；tr=0.15h为依照同公式在r=0.15h处的报警时间，s；tr=0.5w为依照同公式在r=0.5w处的报警时间，s；r为火源与探测器的水平距离，m；h为平面空间高度，m；w为走廊宽度，m；z为火源与探测器的垂直距离，m。

对于楼梯井火灾情况，探测器响应时间可近似认为只与探测器与火源的相对高度有关[16]，因此本文只对高度这一维度进行分析。

本文设计了探测器正常、部分失效、误报3种情景以讨论本方法的合理性。由于误报具有随机性，且失效与误报在不同建筑结构微元场景下无显著差异，因此下文仅讨论狭长走廊的探测器失效与误报情景。

3 计算与仿真结果

3.1 狭长走廊火灾

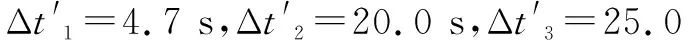
图2 狭长走廊火灾算例示意Fig.2 Schematic diagram of fire simulation in narrow and long corridor

3.1.1 正常工作情景

假设模拟结果为实际报警情况，根据公式(11)～(14)，可得到每1次观测后火源位置的后验概率分布，如图3所示，对于火源的位置信息，算法给出了逐步精准的分布。计算3次观测后的火警真实度曲线，如图4所示，随探测器报警数量的增多，火警真实度值不断升高，说明在真实火警的时间间隔下，模型能够通过设定火警真实度的阈值完成火警的识别。

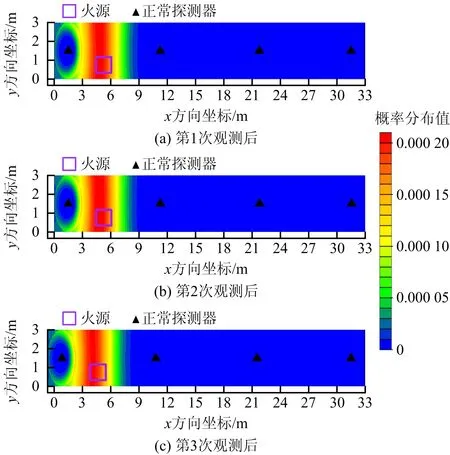
图3 火源位置后验概率分布(走廊场景，正常情景)Fig.3 Posterior probability distribution of fire source location (corridor scene and normal scenario)

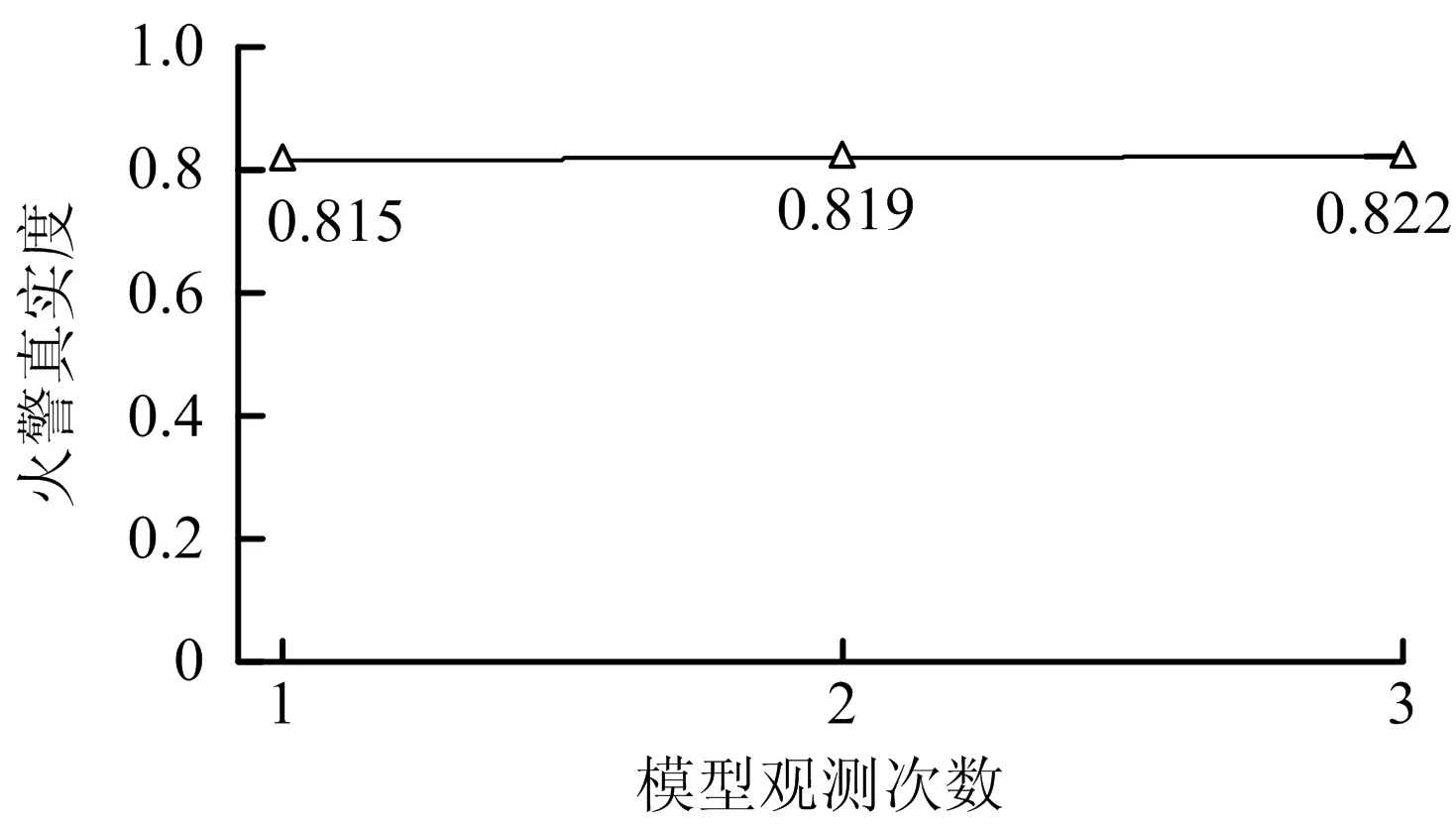
图4 火警真实度趋势(走廊场景，正常情景)Fig.4 Trend of fire alarm authenticity (corridor scene and normal scenario)

3.1.2 部分探测器失效情景

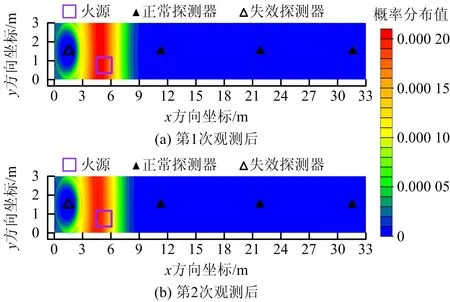
图5 火源位置后验概率分布(走廊场景，失效情景)Fig.5 Posterior probability distribution of fire source location (corridor scene and failure scenario)

图6 火警真实度趋势(走廊场景，失效情景)Fig.6 Trend of fire alarm authenticity (corridor scene and failure scenario)

3.1.3 探测器误报情景

参照常见的同时误报情况，考虑2探测器发生间隔时间较长的报警，假设探测器D1在t1时刻报警，200 s后D2报警，模型在1次观测后得到火源位置的后验概率分布如图7所示。此时微元内各点概率为0，计算得到火警真实度为0。该结果说明模型能够处理一部分探测器误报的情景。显然，当探测器误报时间恰好符合一定规律时，例如报警时间差依次与模拟时间相近，模型也会将其判定为真警，但其发生条件相对苛刻，可能性远小于常见的同时误报情况，此时还可以利用人工手段完成火警的核查工作。

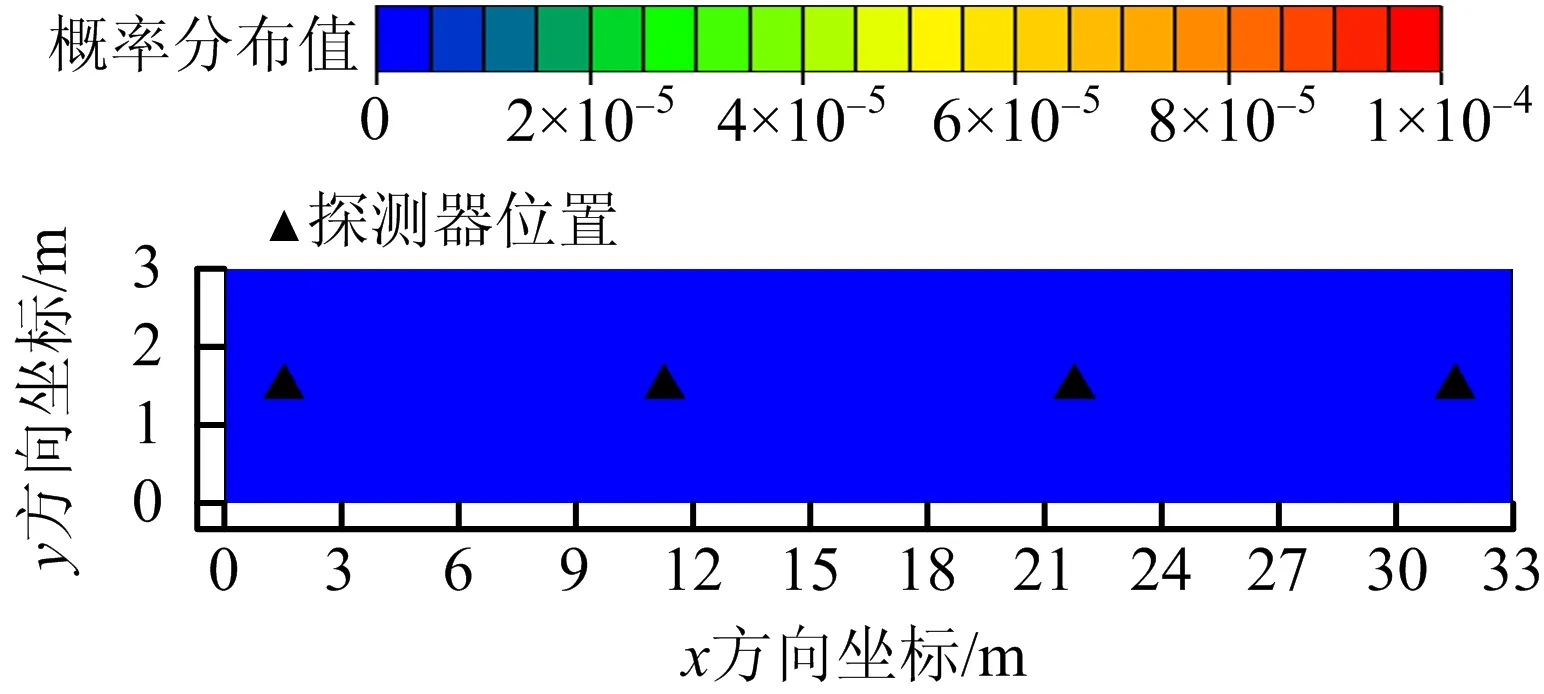
图7 火源位置后验概率分布(走廊场景，误报情景)Fig.7 Posterior probability distribution of fire source location (corridor scene and false alarm scenario)

3.2 腔室火灾

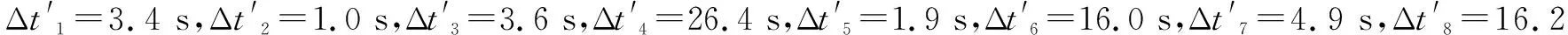
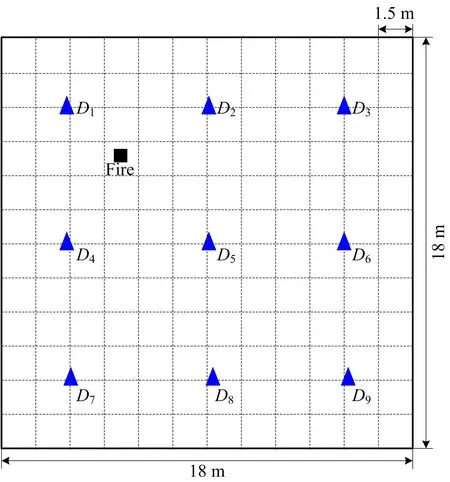
图8 不受限腔室火灾算例示意Fig.8 Schematic diagram of fire simulation in unrestricted chamber

假设各探测器正常工作，得到各次观测后的火源位置后验概率分布，如图9所示，得到各次观测后火警真实度的数值，如图10所示。结果表明在腔室场景中探测器的布置能呈现另一方向的信息，火源位置信息更为确定，火警真实度相对较高，模型能够有效判定真警。

图9 火源位置后验概率分布(腔室场景，正常情景)Fig.9 Posterior probability distribution of fire source location (chamber scene and normal scenario)

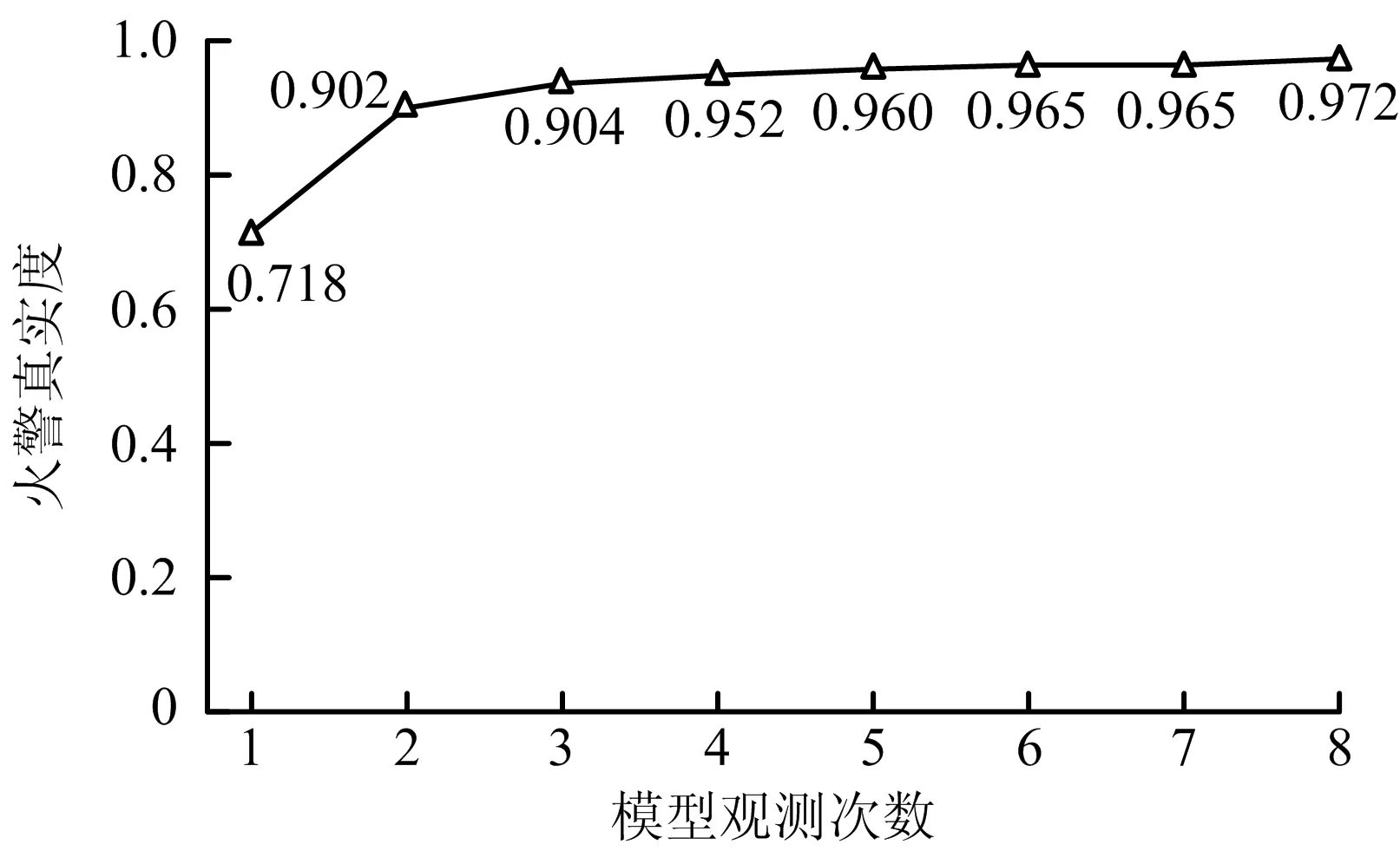
图10 火警真实度趋势(腔室场景，正常情景)Fig.10 Trend of fire alarm authenticity (chamber scene and normal scenario)

3.3 楼梯井火灾

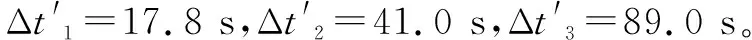
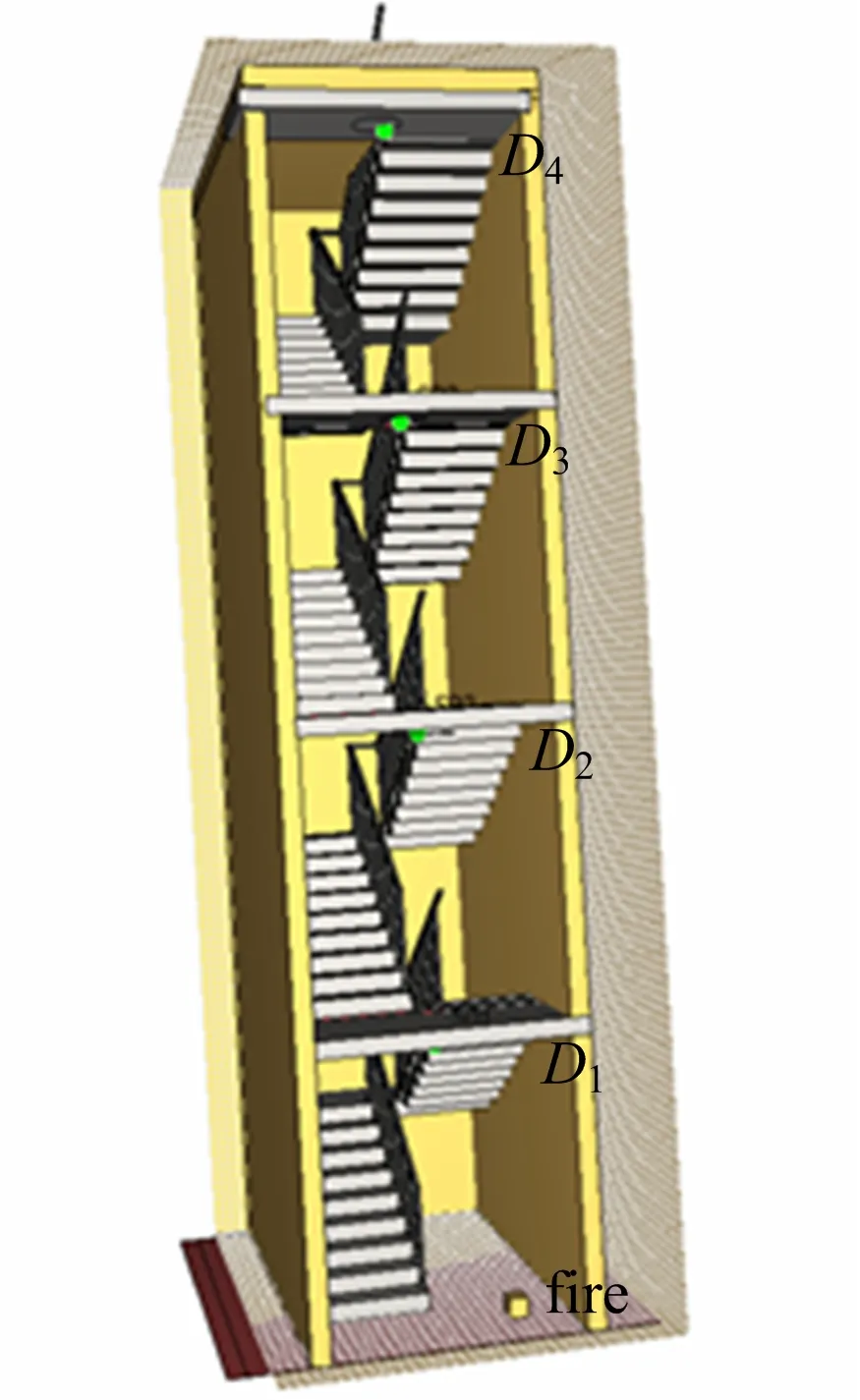
图11 楼梯井火灾算例示意Fig.11 Schematic diagram of fire simulation in stairwell

假设各探测器正常工作，得到各次观测后的火源位置后验概率分布，如图12所示。得到各次观测后火警真实度的数值，如图13所示。随观测次数的增加，模型对火源高度的分布更为集中，火警真实度有明显上升，说明该模型可以应对垂直方向上的火警判定问题。

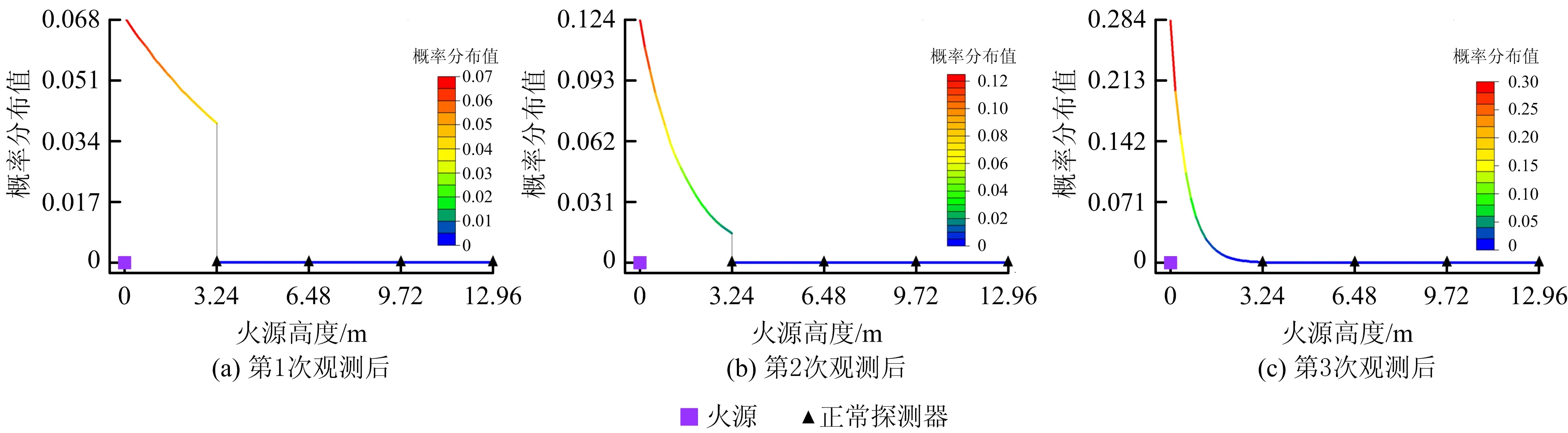
图12 火源位置后验概率分布(楼梯井场景，正常情景)Fig.12 Posterior probability distribution of fire source location (stairwell scene and normal scenario)

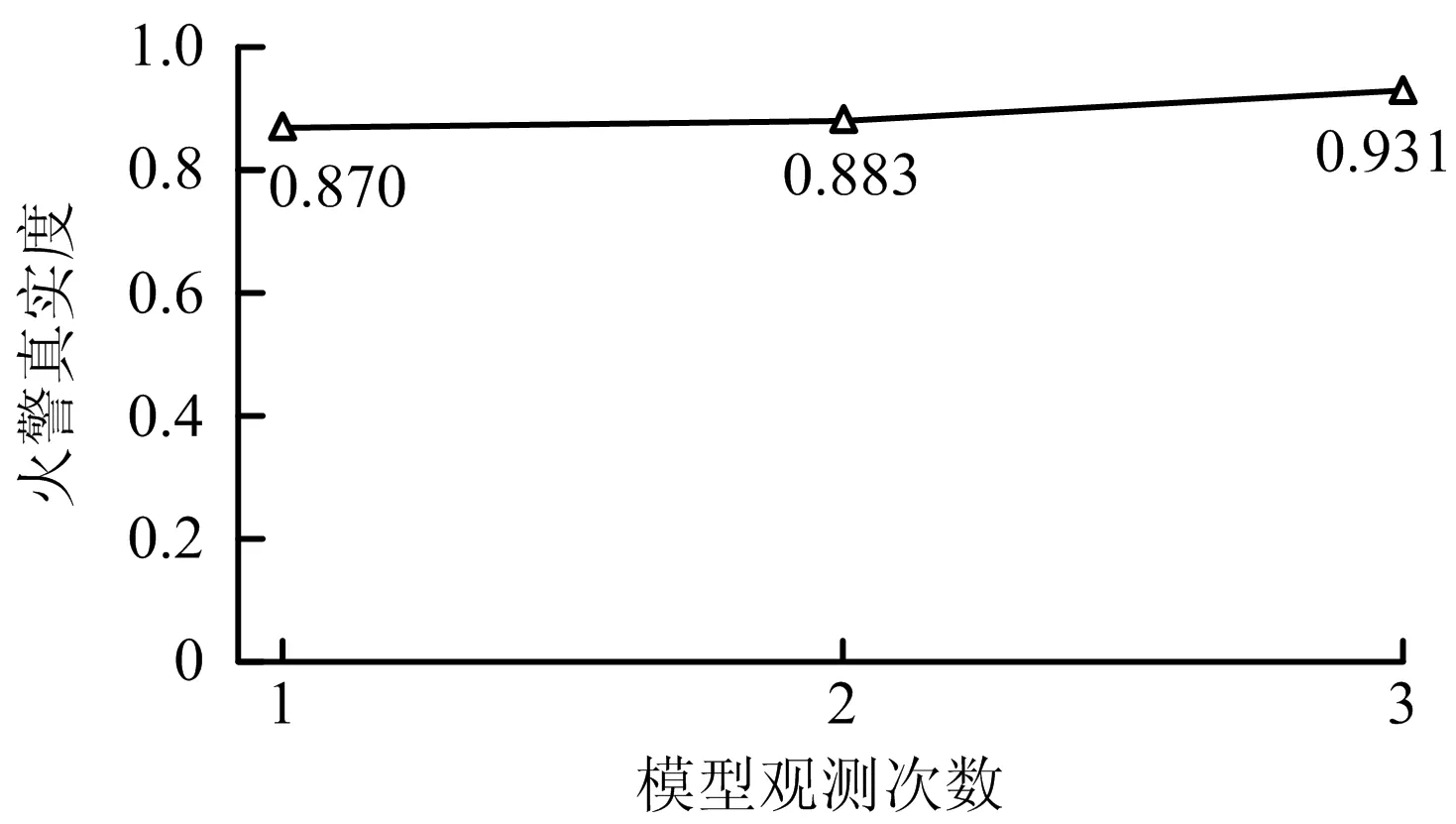
图13 火警真实度趋势(楼梯井场景，正常情景)Fig.13 Trend of fire alarm authenticity (stairwell scene and normal scenario)

4 结论

1)从多探测器耦合检测出发，针对感烟探测器存在的高误报率问题，从理论上说明多探测器方法的有效性，提出基于贝叶斯估计的多探测器火警真实度计算模型。

2)通过对3个典型建筑结构微元火灾场景的模拟分析，验证该算法的可行性，以及应对探测器失效、误报等情景的有效性。该方法的提出将有助于多探测器耦合火警识别方法的工程实现，从理论角度大幅减少单个探测器带来的高误报率问题。

3)基于本文的主要内容，相关研究可以从以下3方面展开：收集真实火灾报警数据或使用实验数据，计算使用该模型后的误报率，研究模型参数的选取，完善模型的性能评价工作；针对多微元的复合结构提出公式的简化思路与模型的改进方法，以提高相关问题的计算效率并降低实施复杂度；研究多探测器复合阈值报警方法，并将其与本模型结合，分析多探测器火警判定方法在复合阈值下的计算模型。