地震下DMTMD对结构刚度和质量参数摄动的鲁棒性

王肖东, 汪 权, 袁加伟

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.阳光城集团,上海 200082)

鲁棒性(Robustness)的概念在20世纪60年代提出后,已在系统控制等领域得到广泛应用。鲁棒性指系统在内部不确定性因素影响和外部环境干扰下仍能保持稳定工作的能力。由于在实际的建筑结构振动控制中,建筑结构的模型参数如结构的刚度和质量参数难以用数学模型来精确描述,结构的不确定性会导致系统控制的不稳定和控制性能恶化,为此研究对结构参数和外部扰动具有较好鲁棒性[1]。

多重调谐质量阻尼器(multiple tuned mass dampers,MTMD)利用一组频率分布在结构被控模态频率周围的单TMD 控制结构的振动行数值模拟与分析。MTMD是把一个大的TMD分成若干小的TMD。各个小的TMD的频率以结构被控模态频率为中心按一定频带宽度纵向分布。MTMD有效改善了单个TMD控制效果不稳定、适用激励频带过窄、可实现性较差的特点。MTMD相比TMD有较好的控制鲁棒性。文献[1]研究了结构刚度摄动而质量不摄动与结构质量摄动而刚度不摄动2种情况,并讨论了MTMD的有效性变化趋势；文献[2]研究了多自由度结构附加MTMD后的频率响应特性,计算了不同频谱特性的地震激励下MTMD系统的时程响应；文献[3]研究了某人行天桥的MTMD消能减振分析,经过MTMD最优参数选取后的主体结构的振动响应衰减比单个TMD更有效,而且在更宽的频带上仍保持有效性；文献[4]以崖门斜拉桥为算例,分析了MTMD对桥梁颤振控制的有效性和鲁棒性,并编制了多模态耦合颤振MTMD控制和参数分析程序。

尽管单调谐质量阻尼器(single tuned mass damper,STMD)及MTMD控制策略发展较为成熟[5-7],但其在实际工程中的应用[8-9]仍是结构振动控制领域的热点问题。尤其是结构的鲁棒性分析,即结构的刚度和质量摄动变化的情况,研究相对较少。

本文MTMD的控制策略分成了沿顶层布置的MTMD控制策略和沿高度分布的分布式多重调谐质量阻尼器(distributed multiple tuned mass dampers,DMTMD)控制策略。采用国际结构振动控制公共平台中的20层Benchmark钢结构模型并利用ANSYS分析软件建立有限元模型。开展MTMD和TMD的结构刚度和质量参数摄动下的控制鲁棒性研究,刚度、质量的单一因素变化的情况和刚度、质量同时变化的情况来分析TMD、MTMD和DMTMD的控制鲁棒性。并为设计MTMD的参数设计提供参考。

1 Benchmark模型及模态分析

本文选用的Benchmark模型是国际结构振动控制公共平台第3阶段20层抗震非线性钢框架结构模型,对其研究可以代表对典型中、高层钢结构建筑的研究,是美国SAC机构于加利福尼亚州真实设计的结构。

(1) Benchmark模型有限元模型。20层抗震Benchmark模型详细参数见文献[10]。

选取整个Benchmark结构的南北方向一榀框架(结构的短方向)进行分析，利用ANSYS软件建立其有限元分析模型。

结构均采用平面杆系模型,梁和柱等框架单元只考虑材料非线性。梁柱单元均采用双线性随动强化模型,以2条直线段描述材料的应力-应变关系。通过弹性模量、屈服应力和切线模量定义应力-应变关系,初始为各向同性材料的小应变问题。本模型为钢结构模型,为金属材料,符合初始各向同性的小应变问题。

梁柱采用具有拉压和弯曲性能的平面弹塑性单轴单元即beam23单元进行模拟,实常数中截面类型设置采用通用截面。定义梁单元弾性模型为2.06×1011Pa,屈服强度为248 MPa,切线模量为2.06×109Pa。柱单元弾性模型为2.06×1011Pa,屈服强度为345 MPa,切线模量为2.06×109Pa(模型详见文献[10])。单元两端每个节点都有3个自由度，即沿节点坐标X、Y方向的平动和绕Z轴的转动。结构中各层梁材料的密度属性选用每层全部质量的1/6,而每层柱材料的密度属性则设置得很小。

在控制系统布置中采用combin14单元来模拟TMD阻尼器弹簧单元,采用mass21单元模拟阻尼器质量单元。combin14和mass21的建立都包括了节点和单元的创建以及参数的赋值,对TMD的研究是通过对combin14单元刚度系数和阻尼系数以及mass21的质量系数的赋值来实现对阻尼器参数的调整。

采用有限元分析软件ANSYS对第3阶段20层Benchmark非线性钢框架结构抗震模型进行建模,整个模型节点个数190,单元个数284,模型如图1所示。

(2) ANSYS模型与ASCE提出的模型模态分析比较。根据中国建筑抗震规范,模态控制的数量取决于模态质量参与系数达到90%,从ANSYS分析可知,前5阶的累计质量分数达98%。通过ASYS的模态分析得到本模型前5阶自振频率与国际ASCE平台所提出的采用Matlab仿真结果进行对比,可以看出结果基本一致,见表1所列。

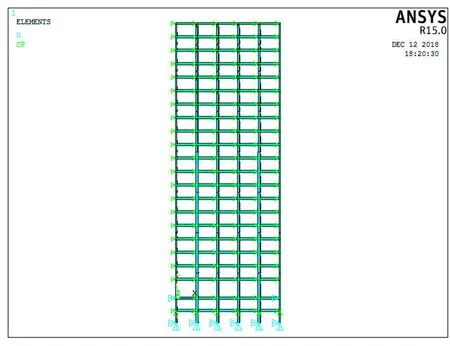
图1 ANSYS有限元模型

表1 模型结构的固有频率对比 Hz

2 控制策略设计与评价指标

2.1 控制策略设计

从ANSYS分析可知,前5阶的累计质量分数达98%,故取前5阶进行DMTMD的设计。在进行DMTMD设计时,每个TMD按前5阶振型振幅最大的位置按高度依次设计。MTMD分5个小TMD安装到最高层的位置。STMD控制质量比μ=0.05,阻尼比ξ=0.05。对于MTMD和DMTMD控制策略设计,5个小TMD的质量比和阻尼比取值相等,并且5个小TMD的质量和等于STMD单个阻尼器的质量。STMD、MTMD、DMTMD控制策略设计分别如图2所示。

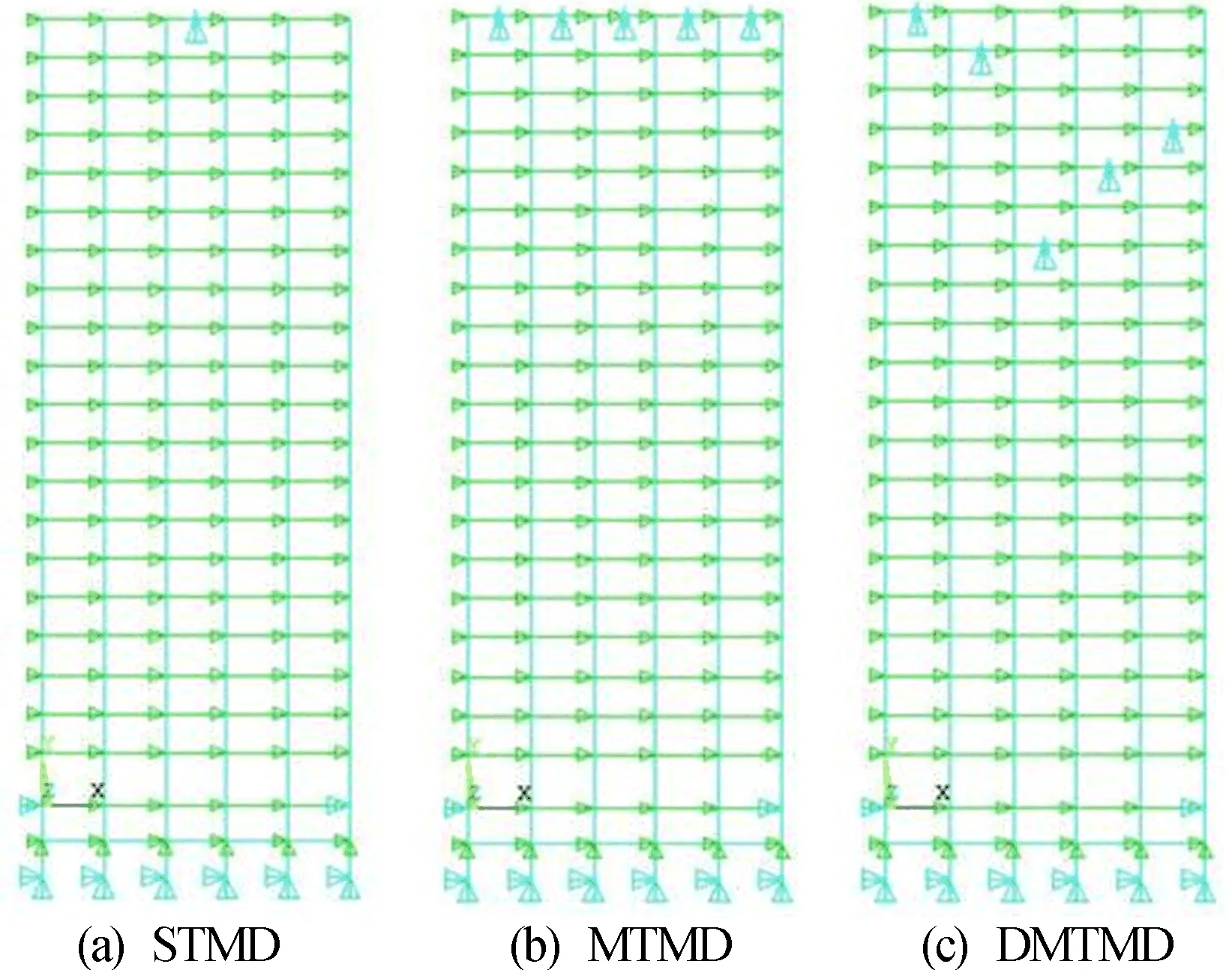
图2 控制策略设计

2.2 评价指标

本文为了评价不同的控制策略,对不同阻尼器布置下的参数摄动结构进行时程分析。在进行时程分析过程中,引入控制性能评价指标J1、J2、J3,定义如下:

(1)

(2)

(3)

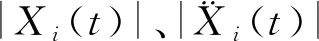
3 单因素控制鲁棒性分析

建筑结构的模型参数如结构的刚度和质量参数难以用数学模型来精确描述,结构的不确定性会导致系统控制的不稳定和控制性能恶化。并且考虑到有限元模型和实际结构有一定的差距,因此考虑本结构质量和刚度参数摄动的控制鲁棒性。比较当结构刚度变化+15%和-15%以及质量参数变化+15%和-15%的控制效果。本文选取Elcentro波、Taft波和天津波3条实际地震波,采用原始地震加速度记录样本采样点间隔时间作为时程分析的时间步长。

3.1 刚度参数摄动控制鲁棒性分析

将有限元模型刚度变化15%,即结构刚度变化+15%和-15%,保持阻尼器其余参数不变,考虑3种控制方案的控制效果鲁棒性。3种控制方案的评价指标见表2、表3所列。

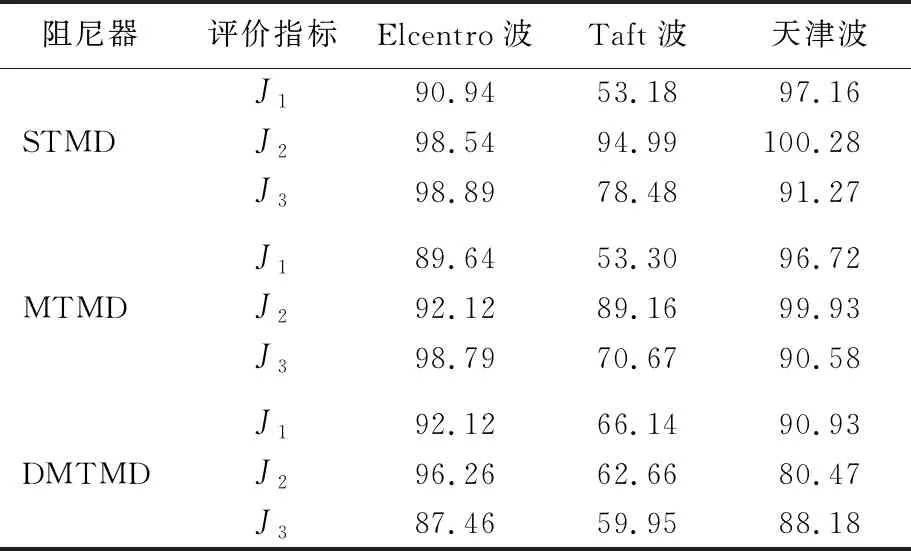
表2 ΔK=+15%K下3种控制方案比较 %

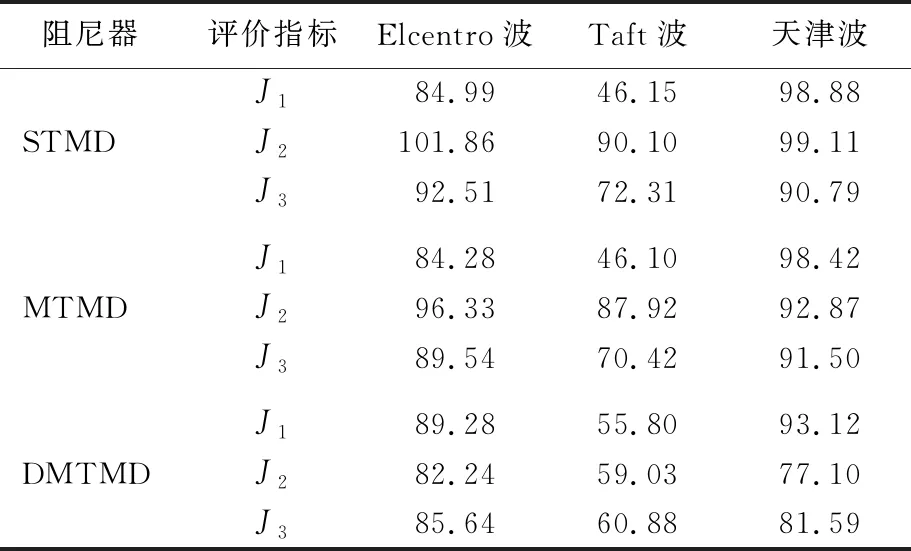
表3 ΔK=-15%K下3种控制方案比较 %

3.2 质量参数摄动控制鲁棒性分析

将有限元模型质量变化15%,即结构质量变化+15%和-15%,保持阻尼器其余参数不变,考虑3种控制方案的控制效果鲁棒性。3种控制方案的评价指标见表4、表5所列。

表4 ΔM=+15%M下3种控制方案比较 %

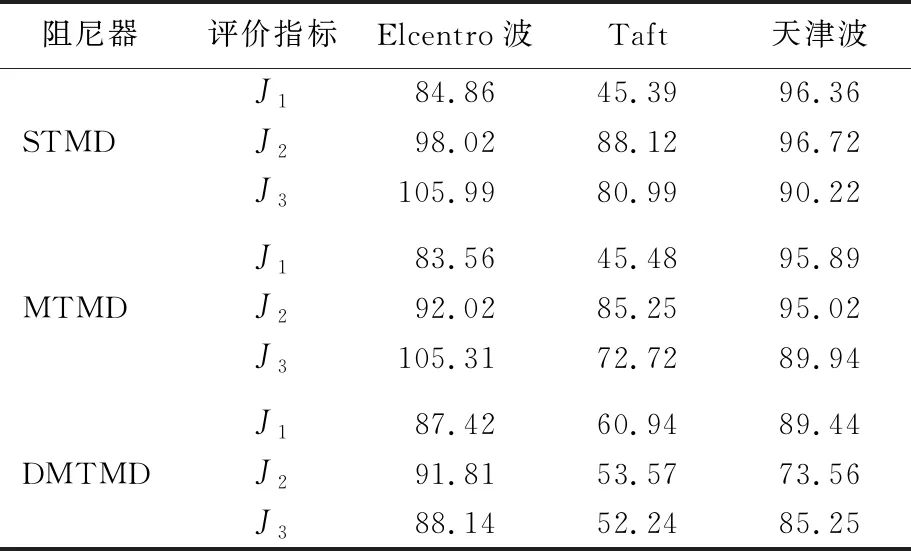
表5 ΔM=-15%M下3种控制方案比较 %

从表2～表5中可以看出,STMD控制方案的设计下,其存在参数失调而使结构振动有增大情况,在刚度或者质量变化15%时,STMD控制均存在不稳定特征,控制的频率过窄,控制鲁棒性较差。尤其是在质量参数摄动的情况下,控制效果更糟,J2(加速度)目标的控制效果均出现了增大的现象。MTMD控制相对稳定,但是仍有少部分评价指标在质量参数摄时下有大于1的情况。DMTMD的控制方案很稳定,因阻尼器的布置相对分散,故评价指标无大于1的情况,尤其在控制加速度和底层剪力方面比STMD、MTMD优越性较大。

4 多因素控制鲁棒性分析

当将有限元模型刚度和质量同时变化15%,即结构刚度+15%、质量变化-15%,结构刚度-15%、质量变化+15%,结构刚度+15%、质量变化+15%,结构刚度-15%、质量变化-15%,保持阻尼器其余参数不变,考虑3种控制方案的控制效果鲁棒性。

4.1 刚度和质量参数异向摄动控制鲁棒性分析

刚度和质量参数异向摄动,即结构刚度+15%、质量变化-15%,结构刚度-15%、质量变化+15%。3种控制方案的评价指标见表6、表7所列。

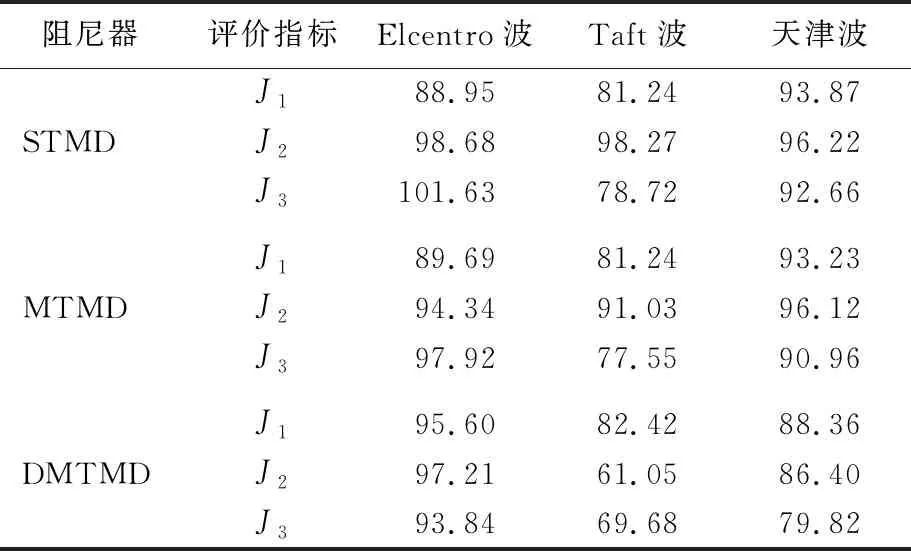
表6 ΔK=+15%K、ΔM=-15%M下3种控制方案比较 %

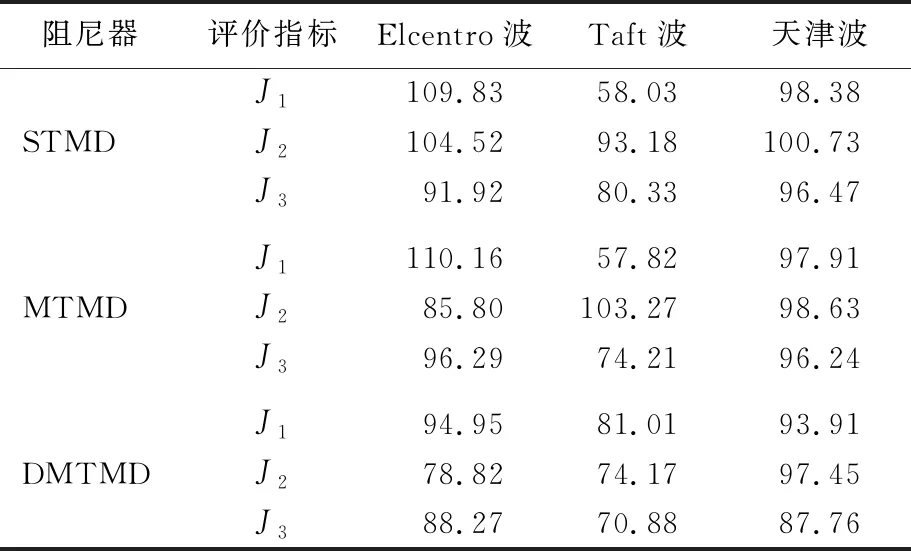
表7 ΔK=-15%K、ΔM=+15%M下3种控制方案比较 %

从表6、表7可以看出,在刚度和质量参数异向摄动时,STMD的控制鲁棒性仍较差,尤其是在ΔK=-15%K、ΔM=+15%M的情况下。MTMD大于1的评价指标数目有所增加,控制鲁棒性相对稳定,DMTMD的评价指标仍无大于1的情况,控制鲁棒性较好。

4.2 刚度和质量参数同向摄动控制鲁棒性分析

刚度和质量参数同向摄动,即结构刚度+15%、质量变化+15%,结构刚度-15%、质量变化-15%。3种控制方案的评价指标见表8、表9所列。

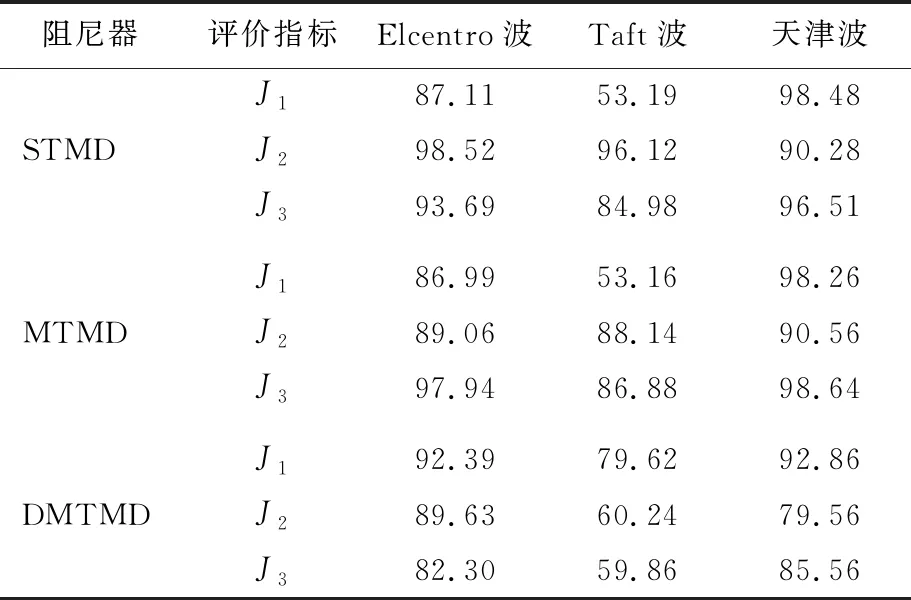
表8 ΔK=+15%K、ΔM=+15%M下3种控制方案比较 %

表9 ΔK=15%K、ΔM=-15%M下3种控制方案比较%

从表8、表9可以看出,STMD的评价指标虽然没有大于1的情况,亦可以看出STMD的控制鲁棒性最差,评价指标的数值大于MTMD和DMTMD。DMTMD的控制鲁棒性较优越,可以用于高层建筑的地震反应控制中。

限于篇幅,本文仅给出Elcentro波、Taft波、天津波作用下,ΔK=-15%K、ΔM=+15%M摄动下3种控制策略的最大层间位移和顶层位移图，如图3～8所示。

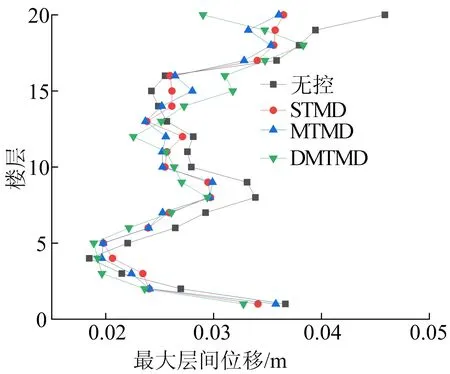
(a) Elcentro波作用下结构最大层间位移

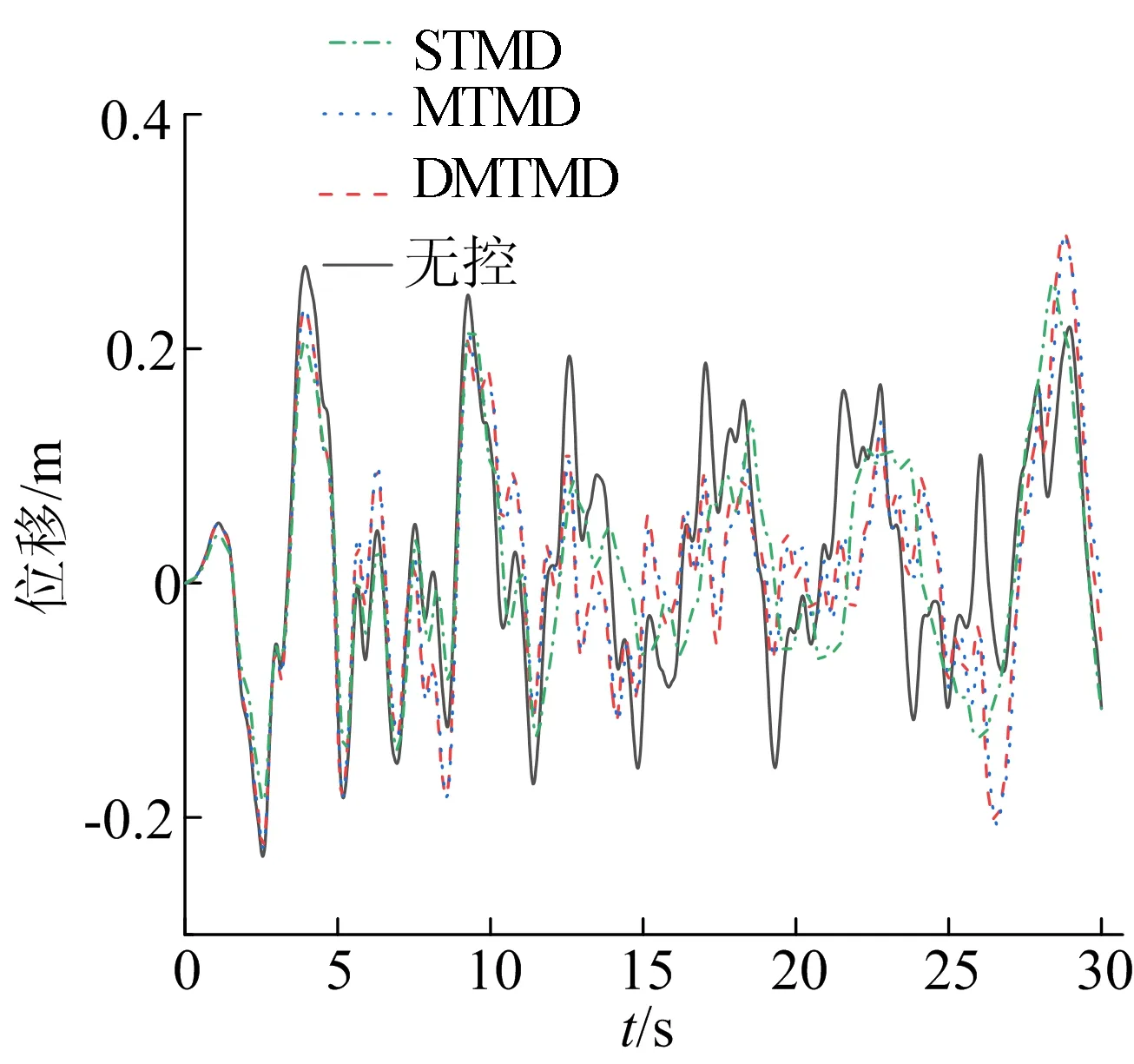
(b) Elcentro波作用下结构顶层位移时程曲线

(c) Taft波作用下结构最大层间位移

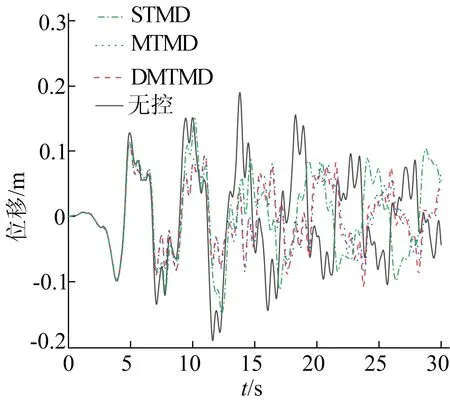
(d) Taft波作用下结构顶层位移时程曲线

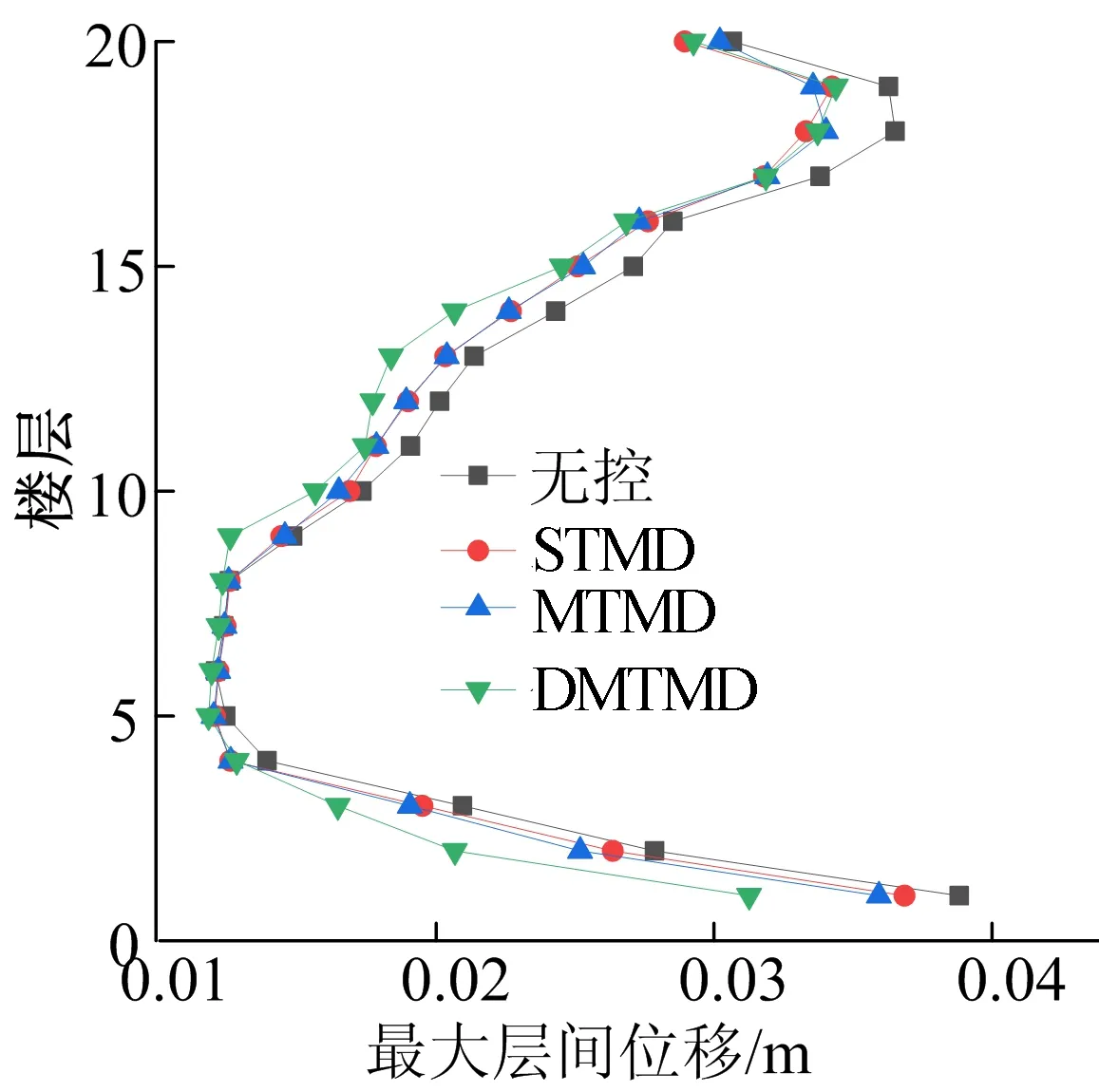
(e) 天津波作用下结构最大层间位移

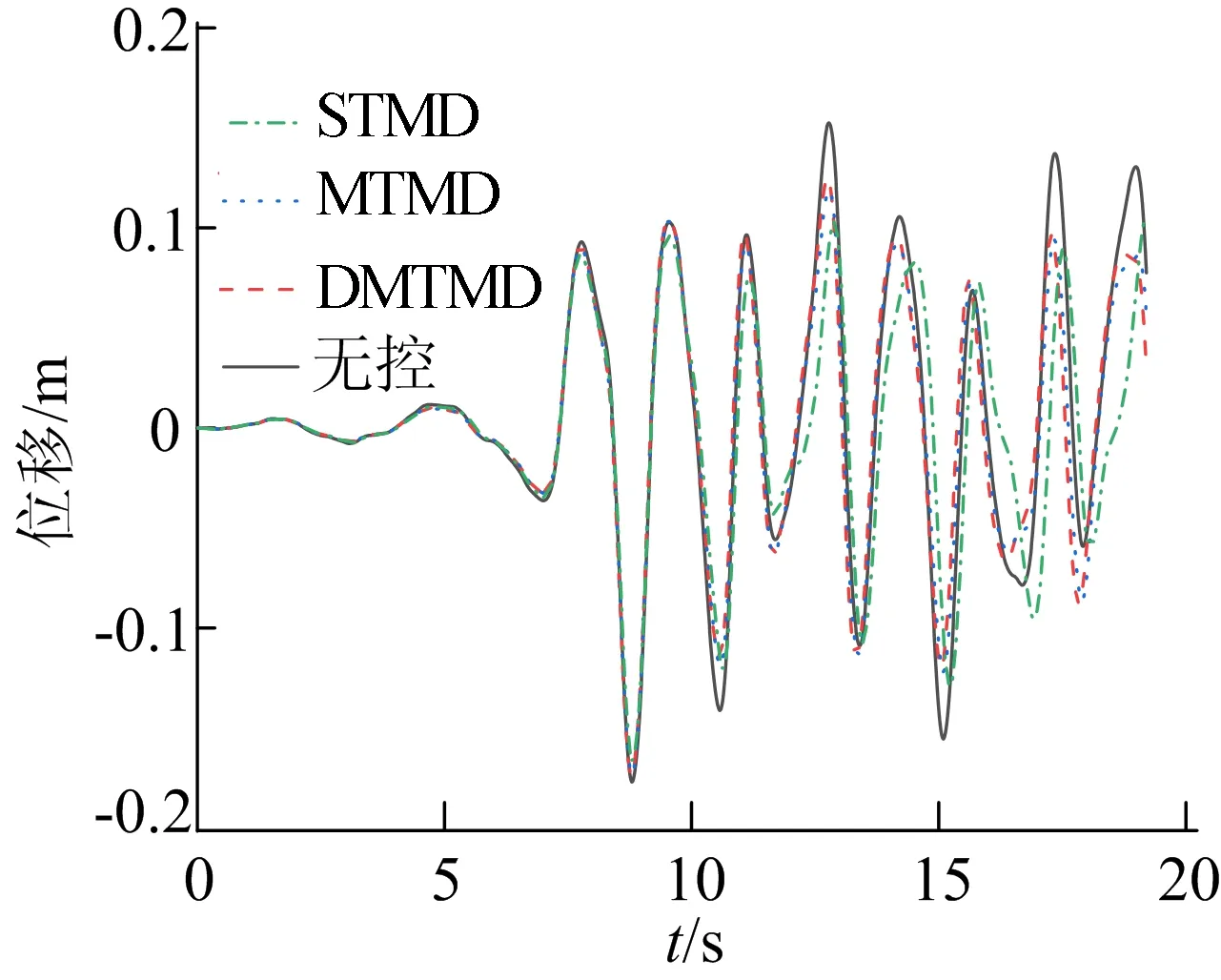
(f) 天津波作用下结构顶层位移时程曲线图3 3种波作用下3种控制策略最大层间位移和顶层位移

5 结 论

本文从高层建筑结构振动控制的鲁棒性出发,利用ANSYS软件对MTMD建筑结构刚度和质量参数摄动的鲁棒性进行研究。选取20层钢框架Benchmark结构为模型,利用ANSYS有限元软件对TMD阻尼器的3种不同布置方案进行鲁棒性仿真分析。结果表明:刚度参数和质量参数摄动时,质量参数摄动对控制效果的影响比刚度参数的影响大;质量参数增加对控制效果的影响比质量参数减小的影响大。本文采用的将MTMD沿结构振型最大处的位置依次布置DMTMD的控制策略,具有良好的鲁棒性,优于相同质量比情况下的仅在结构顶层布置STMD和仅在结构顶层布置MTMD的控制策略。