指数收益率的波动率预测
张云杰

摘要:本文以具有代表性的9个中国股市指数的高频价格和每日收盘价(时间窗口是2013年至2018年)作为数据源,比较广义自回归条件异方差模型(简称GARCH模型,下同)和high-frequency-basedvolatilitymodels(简称HEAVY模型,Shephard和Sheppard(2010),下同)的预测精度。把整体数据源分为样本内数据和样本外数据,样本内数据用于参数估计,样本外数据用于模型预测。然后通过损失函数计算损失值,损失函数值越小,则模型的预测效果越好。最后通过Diebold-Mariano检验统计量判定两个模型优劣的显著性。结果是HEAVY模型整体比GARCH模型预测效果要好。
关键词:GARCH HEAVY 最大似然估计 损失函数 Diebold-Mariano检验统计量
一、引言
20世纪90年代以后,随着信息技术和互联网技术的迅速发展,市场交易信息和资产价格信息获取也更加方便和及时。因此,通过信息技术的帮助,研究人员可以获得高频的交易数据,例如10分钟、5分钟、1分钟的交易数据。同理,获取数据的频率越高,获取的交易信息就越多,分析者做出精准预测的把握性就越大,使得研究结果更精确、更有说服力,可以提高相关领域的风险管理能力。金融风险的大小通常是由标的资产价格或收益的波动率来衡量的,而潜在风险是需要预测相关资产的波动率来衡量的。本文波动率预测模型主要是Shephard和Sheppard(2010)引进的high-frequency-basedvolatilitymodels(简称HEAVY模型,下同)。以GARCH模型(见Bollerslev(1986))作为参照,对中国股市的代表性指数数据分别进行GARCH模型和HEAVY模型建模,分析并對比它们各自的预测值和预测精度,为相关风险投资者和决策者提供更加科学、精准的预测方法。
二、文献回顾
(一)GARCH模型研究
资产的波动率被广泛地应用在期权定价、风险管理中。这种指标的确立促进了自回归条件异方差模型(简称ARCH模型,Engle(1982)和GARCH模型的发展。GARCH模型是在ARCH模型的基础上增加了异方差函数的P阶自相关性。在GARCH模型的结构里,关键成分就是条件方差。当GARCH模型中自回归多项式部分存在单位根时,就可以将模型变成intergratedGARCH(简称IGARCH模型),见Engle和Bollerslev(1986)。其他的对GARCH模型的研究可以参见Bollerslev(2010).
(二)已实现测度模型研究
标准的GARCH模型采用每日收益的平方值来刻画目前资产的波动率水平,比较适合波动率低频变化的情况,不适合用于波动率快速变化的情形,因为在有很多期波动率变化时,GARCH模型拟合波动率变化就很慢,见Andersenetal.(2003)。随着日间交易数据越来越多,一些研究者提出一系列用于度量日间波动率的指标realizedmeasures(已实现测度,简称RM,下同)。本文主要使用其中的一种,即已实现方差(realizedvariance,简称RV,下同)。Andersen和Bollerslev(1998)选择已实现测度为RV的波动率模型来研究噪音的方差和波动率之间的关系。Andersenetal.(2001)使用高频数据研究不同国家汇率的波动率和相关性,认为存在着持续的波动率和相关性的动态变化,且波动率和相关性是已实现的指标而不是潜在的指标。Barndorff-Nielsen和Shephard(2002)使用已实现测度RV来研究收益的随机性,得出了RV误差的渐近分布特性,通过这些特性来估计模型中的待估参数。
(三)基于高频数据的波动率预测模型研究
随着已实现测度模型的快速发展,波动率预测模型的发展也日新月异,呈现出丰富发展态势。Engle(2002)在估计GARCHX类型的模型时,在GARCH方程右侧加入一个RM指标,但他的模型是不完整的,不能够呈现收益率和波动率在超过一个周期之外的情形。Engle和Gallo(2006)引进了第一个完整的波动率预测模型,这个模型对每一个RM都确定一个GARCH结构。Corsi(2009)提出了HAR-RV预测模型来研究已实现波动率的长期记忆性特征,波动率在不同的时间段中有着不同的成分,结果显示了金融资产收益率具有厚尾、长期性、自相关性的特点。Shephard和Sheppard(2010)引进了另一个完整的模型,即HEAVY模型,相比于传统的GARCH模型,HEAVY模型融进了多重潜在的波动过程,包含高频价格信息,即能得出高频的波动率水平,可以进一步发现RM中的额外信息,能够产生样本外的收益。
三、模型介绍
(一)GARCH模型形式
经典的GARCH模型(GARCH1):
(1)
具有单位根的GARCH模型(GARCH2):
(2)
(二)HEAVY模型形式
计算RV的公式:
表示第t天交易的第j个时段的个体。是第t天,时刻交易价格的对数值,是相邻两个时刻指数交易价格取对数值的差,即时刻收益率。
HEAVY1模型主要公式:
(3)
(4)
是第t天收益率的条件方差,是第t天已实现测度的条件期望值。是t-1时刻的信息集,包含低频的收益率(,,…,)和高频的已实现测度(,,…,)。方程(3)中限制条件为ω,α≥0,β∈[0,1);方程(4)中的限制条件为,,≥0,+∈[0,1)。
HEAVY2模型(reparameterization)主要公式:
(5)
(6)
在和稳态的条件下,,。那么我们可以把截距与期望值联系起来,这是HEAVY2的特点。。我们先用均值来估计,和,即,,。这样,HEAVY1可以通过目标参数化转换成HEAVY2。方程(6)的限制条件为。HEAVY2模型与HEAVY1模型的差别只是方程结构和待估参数发生了变化,估计模型和预测模型与HEAVY1模型完全一致。
HEAVY3模型(单位根条件下的HEAVY1)主要公式:
(7)
(8)
(4)在单位根条件下变成了(8)。其中,0<<1。Shephard和Sheppard(2010)引入HEAVY3,是为了提高模型多期预测的能力。
(三)HEAVY参数估计模型
方程(3)使用高斯拟似然函数来估计:
;
其中设定
方程(4)也使用类似于方程(3)的方式来估计:
;
其中设定
在HEAVY1参数估计模型中通过方程的迭代最优化,获得拟似然函数的最大值。令θ=(ω,,,),当θ=时,拟似然函数达到最大值。同理,HEAVY2和HEAVY3的参数估计模型也通过上述方法进行构建、求解。
(四)预测模型
GARCH的预测模型:
以t时刻为预测原点,向前一步预测:
(11)
则,其中,为低频信息集,包含低频的收益率(,,…,)。s>1,向前多步预测为:
(12)
HEAVY的预测模型:
一步向前预测为(由t-1时刻预测t时刻):
(13)
由Shephard和Sheppard(2010)可知,多步向前预测的一般式为(s≥1):
(14)
其中,δ=(),s=4时,表示向前一周波动率预测的总和、当s=21时,表示向前一个月的波动率预测总和。
(五)损失函数
参照Shephard和Sheppard(2010),我们使用拟似然损失函数(QLIK)。在一步或多步向前预测中,对于每个s值:
;
此处=(,)′,通过似然函数可以算出三组参数的估计值,分别为(,)。公式(15)适用于GARCH类模型、HEAVY类模型,本文用样本外收益率的平方代替真实波动率,即用代替真实的波动率,是各个模型向前一步预测或多步预测的波动率值,最后求出损失函数的累积值。
(六)显著性水平检测
判断两个模型预测精度的显著性水平,是通过计算Diebold-Mariano检验统计量(Diebold和Mariano,1995)的值,再与临界值比较。例如A预测模型与B预测模型,定义它们各期损失函数之差的均值:。loss(A)表示A模型的累积损失值,loss(B)表示B模型的累积损失值,p表示向前预测的个数,为第t天A与B模型损失函数的差值。则模型的原假设为
DM统计量的构造如下:(16)
公式(16)中的表示的标准差的一致性估计值,由异方差和自相关一致(HAC)(Newey和West,1987)的標准误差计算得到。当统计值小于临界值时,则显著,拒绝原假设。(10%、5%的显著性水平临界值分别是-1.28、-1.65)
四、实证分析
(一)数据来源和实证步骤
本文先从RESSET/DB(高频数据库)中下载了2013-2018年沪深300指数等9个指数集的实时成交价(频率为5分钟、10分钟、15分钟),再从RESSET/DB(低频数据库)中下载了相应的交易日收盘价。
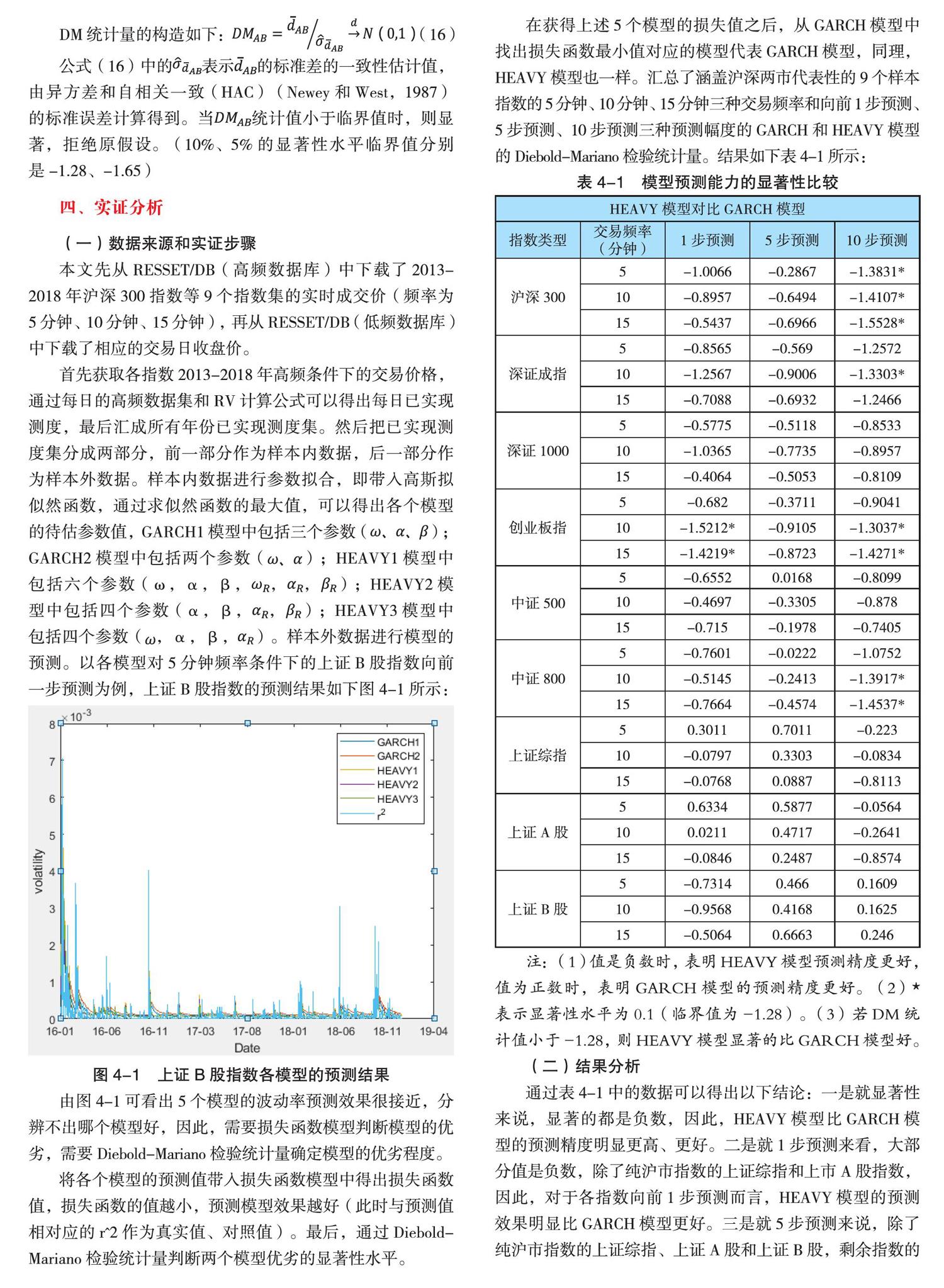
首先获取各指数2013-2018年高频条件下的交易价格,通过每日的高频数据集和RV计算公式可以得出每日已实现测度,最后汇成所有年份已实现测度集。然后把已实现测度集分成两部分,前一部分作为样本内数据,后一部分作为样本外数据。样本内数据进行参数拟合,即带入高斯拟似然函数,通过求似然函数的最大值,可以得出各个模型的待估参数值,GARCH1模型中包括三个参数();GARCH2模型中包括两个参数();HEAVY1模型中包括六个参数(ω,α,β,,,);HEAVY2模型中包括四个参数(α,β,,);HEAVY3模型中包括四个参数(,α,β,)。样本外数据进行模型的预测。以各模型对5分钟频率条件下的上证B股指数向前一步预测为例,上证B股指数的预测结果如下图4-1所示:
图4-1 上证B股指数各模型的预测结果
由图4-1可看出5个模型的波动率预测效果很接近,分辨不出哪个模型好,因此,需要损失函数模型判断模型的优劣,需要Diebold-Mariano检验统计量确定模型的优劣程度。
将各个模型的预测值带入损失函数模型中得出损失函数值,损失函数的值越小,预测模型效果越好(此时与预测值相对应的r^2作为真实值、对照值)。最后,通过Diebold-Mariano检验统计量判断两个模型优劣的显著性水平。
在获得上述5个模型的损失值之后,从GARCH模型中找出损失函数最小值对应的模型代表GARCH模型,同理,HEAVY模型也一样。汇总了涵盖沪深两市代表性的9个样本指数的5分钟、10分钟、15分钟三种交易频率和向前1步预测、5步预测、10步预测三种预测幅度的GARCH和HEAVY模型的Diebold-Mariano检验统计量。结果如下表4-1所示:
(二)结果分析
通过表4-1中的数据可以得出以下结论:一是就显著性来说,显著的都是负数,因此,HEAVY模型比GARCH模型的预测精度明显更高、更好。二是就1步预测来看,大部分值是负数,除了纯沪市指数的上证综指和上市A股指数,因此,对于各指数向前1步预测而言,HEAVY模型的预测效果明显比GARCH模型更好。三是就5步预测来说,除了纯沪市指数的上证综指、上证A股和上证B股,剩余指数的DM统计值几乎都是负数。因此整体来看,还不能确定两个模型中哪个模型更好。但是分开来看,纯沪市指数向前5步预测,GARCH模型预测更好,除了纯沪市指数外其他指数,HEAVY模型预测效果更好。四是就10步预测来说,绝大部分的DM统计值都为负数,除了上证B股指数(不显著)。因此,对于各指数向前10步预测而言,HEAVY模型的预测效果明显比GARCH模型更好,且显著。五是从交易频率来看,标记“*”的统计值,大部分处在频率为10分钟和15分钟,仅沪深300指数的5分钟、10步预测的统计值达到“*”水平。因此,频率为10分钟和15分钟的HEAVY模型比GARCH模型更加精确,更加显著。六是通过纯沪市指数的上证综指、上证A股指数和上证B股指数的DM统计值来看,暂时还分辨不出两类模型的优劣,因为统计值有正、有负,没有规律。
五、总结与建议
(一)总结
本文通过两类波动率预测模型GARCH模型(两种)与HEAVY模型(三种)对沪深两市具有代表性的9种指数进行建模分析。文章中另外两个维度分别是交易频率和预测步长,是为了更好地从纵向和横向对比得出各个模型的优劣。本文用前三年的数据预测后三年的波动率,再和代替真实波动率的r^2进行比较,确定损失值。在参数估计和预测过程中,先通过RV公式计算出已实现测度集,分成样本内和样本外两部分,样本内数据用于参数估计,样本外数据用于波动率预测。然后将各个模型得出的预测值带入损失函数方程中,得出累积损失值。最后通过Diebold-Mariano检验统计量的正负值判断两类模型预测精度的优劣,通过显著性水平判断,确定某个模型是否比另一个模型预测效果明显要好。主要结果就是由表4-1得出的6条结论,整体而言,HEAVY模型比GARCH模型的预测精度更高,尤其是在10步预测,10分钟或15分钟的频率下更加显著,预测效果更好。
(二)建议
由表4-1可知,除了最后三个纯沪市指数之外,其他所有指数的DM统计量几乎都是负值,可以表明HEAVY模型是优于GARCH模型的,呈现显著性的地方更能说明这一点。可是,通过最后三个指数还得不出哪类模型效果好,在不同的维度下,各有各的薄弱优势,因为几乎都不显著。建议:对于证券投资者和风险投资者而言,若是目标对象是非纯沪市指数标的组合(即上证指数),则使用HEAVY模型进行指数波动率预测比GARCH模型效果更好,且很明显,无论处在何种维度条件下,这个结论几乎都成立。改进方向:一是扩大指数范围,再加入沪深两市、科创板、创业板、中小板等比较有代表性的指数进行波动率预测。二是扩大频率范围,再引入20分钟和30分钟交易频率的数据。三是加大预测步数,由于预测步数越长,损失值越大,预测越不精确,因此只增加一种向前22步预测即可。四是进行数据清理,对发现极端值的情况下,进行阈值约束。
参考文献:
[1]AndersenTG,BollerslevT.Answeringtheskeptics:Yes,standardvolatilitymodelsdoprovideaccurateforecasts[J].Internationaleconomicreview,1998,39(4):885-905.
[2]AndersenTG,BollerslevT,DieboldFX,etal.Thedistributionofrealizedexchangeratevolatility[J].JournaloftheAmericanstatisticalassociation,2001,96(453):42-55.
[3]AndersenTG,BollerslevT,DieboldFX,etal.Modelingandforecastingrealizedvolatility[J].Econometrica,2003,71(2):579-625.
[4]BollerslevT.Generalizedautoregressiveconditionalheteroscedasticity[J].Journalofeconometrics,1986,31(3):307-327.
[5]BollerslevT.GlossarytoARCH(GARCH),InT.Bollerslev,J.Russell,andM.Watson(eds.),VolatilityandTimeSeriesEconometrics:EssaysinHonorofRobertEngle.2020,oxfordUniversityPress.
[6]BarndorffNielsenOE,ShephardN.Econometricanalysisofrealizedvolatilityanditsuseinestimatingstochasticvolatilitymodels[J].JournaloftheRoyalStatisticalSociety:SeriesB(StatisticalMethodology),2002,64(2):253-280.
[7]CorsiF.Asimpleapproximatelongmemorymodelofrealizedvolatility[J].JournalofFinancialEconometrics,2009,7(2):174-196.
[8]Dieblod,F.,andR.Mariano.1995.ComparingPredictiveAccuracy.JournalofBusinessandEconomicStatistics,vol.13,253-265.
[9]EngleRF.AutoregressiveconditionalheteroscedasticitywithestimatesofthevarianceofUnitedKingdominflation[J].Econometrica:JournaloftheEconometricSociety,1982:987-1007.
[10]Engle,R.F.andT.Bollerslev.ModelingthePersistenceofConditionalVariances[J].EconometricReviews,1986,5,1-50.
[11]Engle,R.F.2002.NewfrontiersforARCHmodels.journalofAppliedEconometrics17:425-446.
[12]EngleRF,GalloGM.Amultipleindicatorsmodelforvolatilityusingintra-dailydata[J].JournalofEconometrics,2006,131(1):3-27.
[13]Newey,WandK.West.1987.ASimple,PositiveSemi-Definite,HeteroskedasticityandAutocorrelationConsistentCovarianceMatrix.Econometrica,vol.55,703–708.
[14]ShephardN,SheppardK.Realisingthefuture:forecastingwithhigh-frequency-based volatility(HEAVY)models[J].JournalofAppliedEconometrics,2010,25(2):197-231.
作者單位:首都经济贸易大学

