12.3.1等腰三角形（第一课时）

黄辉 陈波

教学目标：

1.理解并掌握等腰三角形的定义，探索等腰三角形的性质;能够用等腰三角形的性质解决相应的数学问题.

2.在探索等腰三角形的性质的过程中体会知识间的关系，感受数学与生活的联系.

3.培养学生分析解决问题的能力，使学生养成良好的学习习惯.

教学重点：

1.等腰三角形的概念及性质. 2.等腰三角形性质的应用.

教学难点：

等腰三角形三线合一的性质的理解及其应用.

教学方法：

创设情境-主体探究-合作交流-应用提高.

教具準备：

师：多媒体课件、投影仪;

生：硬纸、剪刀

教学过程：

一、创设情境

前面的学习中，认识了轴对称图形，探究了轴对称的性质.这节课从轴对称的角度来认识一些我们熟悉的几何图形.来研究：①三角形是轴对称图形吗？②什么样的三角形是轴对称图形？

二、自主探究（分组活动）

活动A：把一张长方形纸对折，在折痕处剪去一个直角，再把它展开，得到一个三角形，此三角形有何特点？

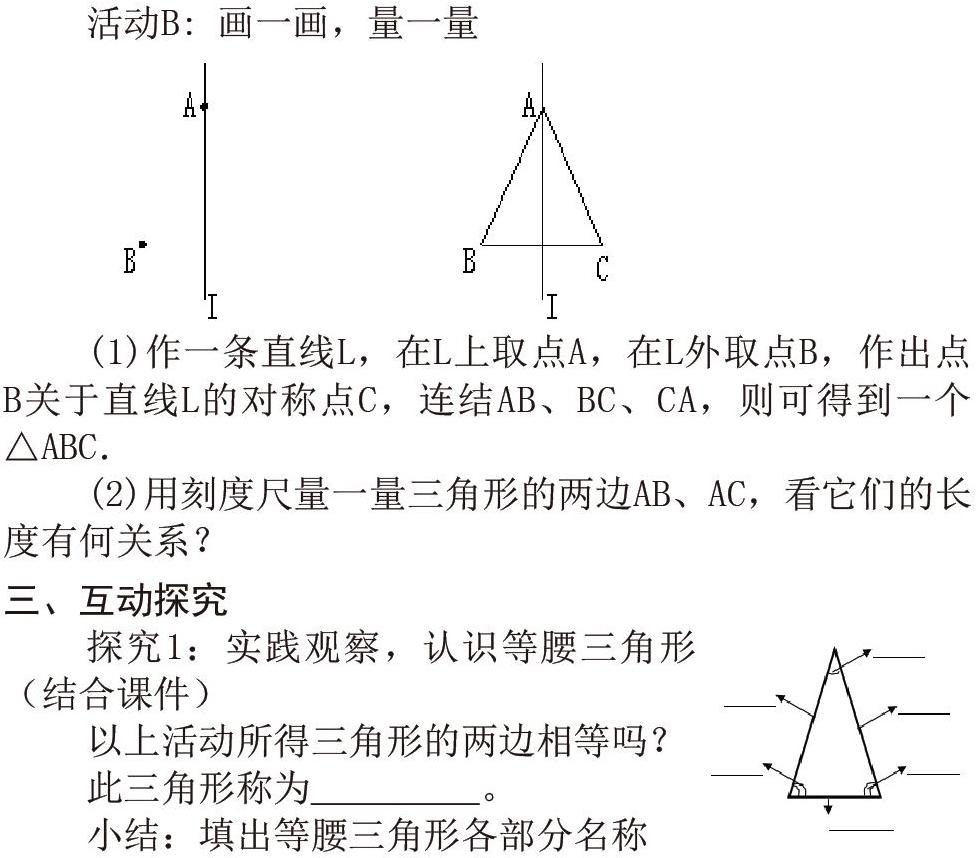
活动B： 画一画，量一量

（1）作一条直线L，在L上取点A，在L外取点B，作出点B关于直线L的对称点C，连结AB、BC、CA，则可得到一个△ABC.

（2）用刻度尺量一量三角形的两边AB、AC，看它们的长度有何关系？

三、互动探究

探究1：实践观察，认识等腰三角形（结合课件）

以上活动所得三角形的两边相等吗？

此三角形称为 。

小结：填出等腰三角形各部分名称

探究2：等腰三角形的性质

问题1.等腰三角形是轴对称图形吗？请找出它的对称轴.

问题2.折叠或量，看看等腰三角形的两底角有什么关系？

问题3.顶角的平分线所在的直线是等腰三角形的对称轴吗？

问题4.底边上的中线所在的直线是等腰三角形的对称轴吗？底边上的高所在的直线呢？

1.学生通过刚才自主探究，大胆猜想以上问题的结果。

2.教师用几何画板直观演示并引导学生观察等腰三角形的性质。（对称性，等边对等角，“三线合一”）

小结：等腰三角形的性质：

3.你能证明以上性质吗？

问题（1）性质1（等腰三角形的两个底角相等）的条件和结论分别是什么？

（2）怎样用数学符号表达条件和结论？

（3）如何证明？

（4）受上述启发，能证明性质2吗？

（阅读课本P50页例1以前的内容）

请以“作顶角的角平分线”为辅助线，证明以上性质。（A 组同学完成以下填空，B组独立证明）教师巡视辅导点评。

5、提问：作底边上的高，又如何证明？（一同学讲证明思路）

四、巩固练习

五、小结

本课你知道了等腰三角形哪些性质？

六、课外作业