一种改进的层次分析法在出行方式选择中的应用

舒孝珍

(成都师范学院数学学院，四川成都 611130)

0 引言

随着社会的进步与时代的发展，人们的出行方式也越来越多元化.与文章[1]不同的是，本论文此次利用了一种改进的层次分析法[2，3]研究了游家渡小区上班族的出行方式，仍然以地铁，私家车，共享汽车这3种主要的交通工具为研究对象，比较分析了改进的层次分析法与传统的层次分析法在解决决策问题时的优劣.

1 改进的层次分析法

1.1 层次分析法的一般步骤[1,4,5]

美国运筹学家A.L.Saaty教授提出的层次分析法的一般步骤可以概括为

步骤1 建立层次结构模型；

步骤2 根据九标度法建立判断矩阵；

步骤3 计算判断矩阵的权向量并做一致性检验；

步骤4 计算层次总排序并做组合一致性检验.

应用Saaty教授提出的层次分析法分析问题时，需要对建立的每一个判断矩阵进行一致性检验，当一致性检验不能通过时，需要修正判断矩阵，再次进行一致性检验，此过程一直持续到判断矩阵通过一致性检验为止.当判断矩阵比较多时，采取传统的层次分析法解决问题就会增加计算的困难性与繁琐性，因此，国内外学者提出了很多改进的方法[7-11].

1.2 改进的层次分析法的一般步骤[2,3,5,6]

改进的层次分析法采用三标度法建立判断矩阵，利用最优矩阵的概念导出拟优一致矩阵，直接求出权重，从而不需要进行一致性检验.

改进的层次分析法的步骤

步骤1 建立层次结构模型

步骤2 根据三标度法建立判断矩阵A

步骤3 构造判断矩阵B

步骤4 求判断矩阵B的最优传递矩阵C

步骤5 求判断矩阵B的拟优一致矩阵D

dij=10cij.

步骤6 计算权重

2 在出行方式选取中的应用

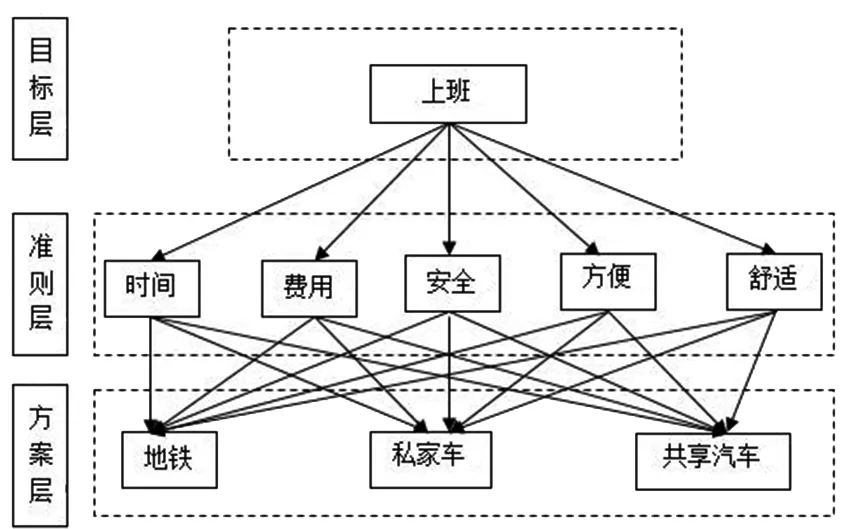
图1 出行方式评价指标体系Fig.1 Travel mode evaluation index system

2.1 建立层次结构模型

通过对游家渡小区上班族出行方式及其影响因素的分析，建立层次结构模型[1]如图1所示.

2.2 建立判断矩阵和导出拟优一致矩阵

通过调查问卷和综合专家意见，利用三标度法，建立准则层因素的判断矩阵如下

由判断矩阵A可知

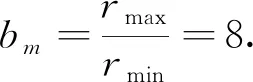
下面依次计算判断矩阵B，最优传递矩阵C和拟优一致矩阵D.

2.3 权重计算

权重的计算可采用MATLAB编程来实现，建立M文件程序如下

D =[1,4.162 3,1,4.162 3,11.542 5;0.240 3,1,0.240 3,1,2.772 7;1,4.162 3,1,4.162 3,

11.542 5;0.240 3,1,0.240 3,1,0.772 7;0.086 6,0.360 7,0.086 6,0.360 7,1];

[V D]=eig(D);

W=V(:,1)/sum(V(:,1))

运行结果：

W =(0.395 0，0.094 9，0.395 0，0.080 8，0.034 2)

即目标层对准则层的层次单排序权重W=(0.395 0，0.094 9，0.395 0，0.080 8，0.034 2)

采取同样的方法，可以计算出方案层对准则层层次单排序权重

W1=(0.553 8, 0.223 1, 0.223 1)

W2=(0.553 8, 0.223 1, 0.223 1)

W3=(0.553 8, 0.223 1, 0.223 1)

W4=(0.128 3, 0.595 4, 0.276 4)

W5=(0.128 3, 0.595 4, 0.276 4)

记层次总排序为W*，采取模糊综合评判法[4]计算W*，记准则层对方案层的单因素评判矩阵为R，则

于是，

W*=W·R=(0.504 8,0.265 9,0.229 2)

因此，游家渡小区上班族出行方式选取为优先考虑地铁，其次是私家车，最后是共享汽车，此结论与文章[1]所得结论一致.

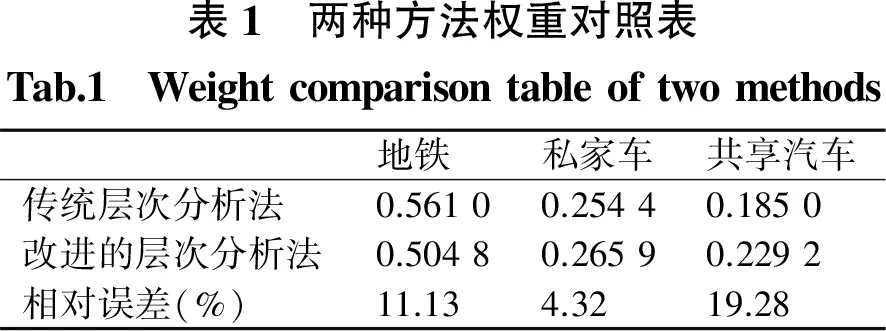
2.4 两种方法比较分析

为了说明改进的层次分析法具有合理性，把通过改进的层次分析法计算得到的权重值与通过传统的层次分析法[1]计算得到的权重值进行比较，比较结果见表1，从表1可以看出，两种方法的相对误差控制在20%以内，且所得结论相同，说明改进的层次分析法是合理的.

3 结语

与传统的层次分析法比较，改进的层次分析法最大的优势在于避免了一致性检验的步骤，因而简化了某些计算过程.文章利用了三标度法建立判断矩阵，虽然也具有一定的主观性，但和九标度法比较起来，降低了两两元素比较的判断难度.