地面效应对反推状态下发动机进口流场影响数值研究

周凯，王志强

(南京航空航天大学 能源与动力学院，江苏 南京 210016)

0 引言

随着涡扇发动机涵道比的增加，风扇流量大幅度增加[2]，引起反推力装置流通面积增加，增大反推力装置轴向尺寸，缩短了反推力装置与地面距离，加剧了反推气流与地面相互作用。

地面应该模拟成一个以自由流速度移动的地板，当地板移动速度达到自由流速度时可消除固定地面产生的边界层影响。2005年G. H. Hegen利用带有移动带的DNW-LLF风洞对TPS模型开展不同滑跑速度下地面效应对反推气流重吸入的影响。有无移动带地板风洞试验示意图如图1所示。国内反推力装置性能试验大都在带有固定地板的风洞测试，对地面效应影响的研究较少[3-5]。

图1 有无移动带地板风洞试验示意图

本文针对某大涵道比涡扇发动机的简化模型，开展着陆滑跑状态下反推气流流场的数值研究，分析不同滑跑速度下地面效应对反推状态下大涵道比涡扇发动机进口流场畸变影响。

1 建模与网格划分

本文研究对象为大涵道比涡扇发动机1∶1全尺寸模型。主要由发动机短舱、吊架、进气锥、内涵喷管和叶栅式反推装置组成，如图2所示。

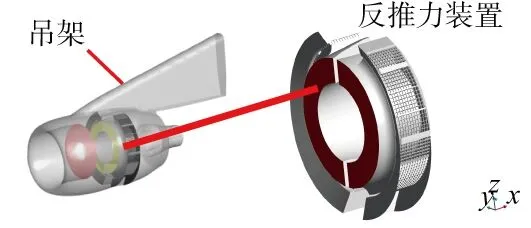
图2 计算对象示意图

在发动机外建立了半圆柱外流区域，如图3(a)所示。发动机中轴线距离地面为H，发动机直径D(此时H/D约为2)，发动机轴向长度为L。计算域半径为14D，计算域长度取为发动机轴向长度L的10倍，计算域进口距离发动机进口约为5.5L。

采用ICEM对计算域进行网格划分，外流场流域最大网格尺度为1024mm，在流动复杂区域发动机周围和发动机进气道附近设置双加密区，如图3(b)所示，发动机进气唇口区域最大网格尺度为16mm，并在壁面设置了10层边界层网格，第一层网格为0.2mm，延展比为1.2。反推力装置域相对尺寸较小，最大网格尺寸设为32mm(图3(c))，其中叶栅区面网格最大尺寸为2mm(图3(d))，并在外流域与反推力装置内域交界处反推气流出口设置相同网格参数，最后生成网格单元约为2100万(elements)，记为Grid_2100万。通过合理改变上述网格参数，共生成4套网格分别为Grid_1000万、Grid_1600万、Grid_2100万、Grid_5500万。

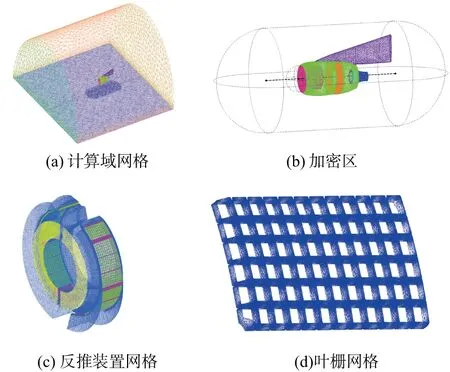
图3 计算网格示意图

2 数值计算方法

2.1 计算方法

本文数值模拟采用ANASYS CFX软件。为了验证本文数值模拟方法的可靠性和所采用网格密度、湍流模型的合理性，首先对台架试验的5个不同状态点开展反推气流流场的数值模拟研究，通过与试验数据对比，验证本文采用的数值模拟方法的准确性。

计算时的边界条件给定如图4所示：外流域主要由远场、远场进口、远场出口以及地面边界组成，在验证数值模拟方法准确性计算中三远场为开放边界，给定试验记录的环境大气总温、总压；外流域的下边界为无滑移壁面，用于模拟试验中固定地面；发动机进口截面设定为质量流量速率出口；发动机内涵喷管进口和反推力装置进口为计算域的进口边界，给定相应试验状态下的总温、总压。

师：拆开容易，拼装难呀！同学们能把拆开的魔方装回去吗？（生纷纷响应）现在就来比一比谁拼得快，完成的同学老师给他戴上一个皇冠。

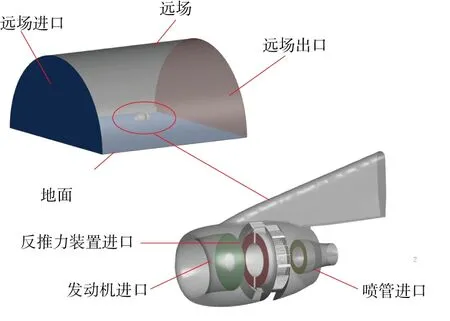
图4 边界条件示意图

2.2 网格密度和湍流模型选定

国内外已开展了大量的大涵道比涡扇发动机反推气流流场数值模拟研究。DE Andrade F O等人[6-10]分别选用k-ω、SST、k-ε湍流模型对大涵道比涡扇发动机反推扰流流场展开了数值模拟研究。

从上述研究可以看出，反推流场数值模拟方法仍存在以下问题：第一，湍流模型的选定仍是关键；第二，研究对象几何模型复杂，部件尺寸差异较大，网格参数是影响数值模拟精确性的重要因素。

本文分别采用4套网格对台架试验的5个状态点开展反推气流流场的数值模拟研究。

图5为不同网格量计算得到的不同状态点下推力与试验值的相对偏差。从上述4套网格计算结果可以看出，各套网格计算得到的推力值与试验结果的偏差趋势基本一致，总体网格量1000万计算结果较其他3套网格推力相对误差更大，基本都超过5%，网格增加至2100万后，数值模拟结果与试验推力贴合最好，推力相对误差集中在±5%左右，故采用Grid_2100万为本次计算网格。其中，推力相对误差ε如下式：

式中：TCFD表示数值模拟计算推力；TTest表示推力试验值。

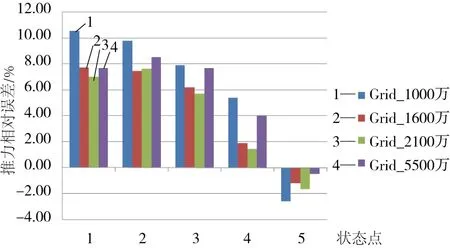
图5 不同网格密度反推力相对误差图

本文在选用Grid_2100万网格的前提下选取了SST模型、标准k-ω模型以及标准k-ε模型，分别开展了反推状态下的排气系统流场计算。

从图6可以看出，各湍流模型计算得到的发动机推力与试验值的偏差随工况的变化趋势是一致的。从图可以看出，标准k-ω模型计算得到的发动机推力最大，而标准k-ε模型的计算结果与试验结果最接近。

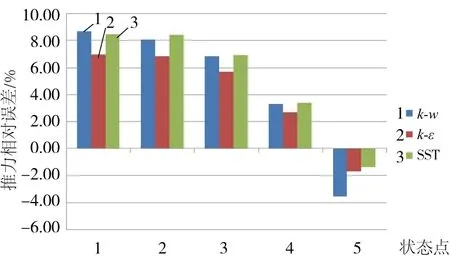
图6 不同湍流模型反推力相对误差图

3 地面效应数值模拟结果分析

本文采用Grid_2100万选择标准k-ε模型，分别选择0.03、0.04、0.06、0.08、0.10、0.15、0.22、0.25等来流马赫数[11]为多个稳态瞬间进行定常计算。计算中改远场进口为速度进口，给定相应的来流马赫数，其余边界设定保持不变。通过改变地面为固定无滑移壁面和移动无滑移壁面(速度与远场进口相等)，分析地面效应对反推状态下大涵道比涡扇发动机进口流场影响。选用ARP1420[12]所规定的周向稳态总压畸变指数Δσ，计算发动机进口AIP(aerodynamic interface plane)截面上的周向稳态总压畸变指数，来评估由地面效应引起的发动机进口流场的总压不均匀性。

为了获取AIP截面上的畸变指数，在AIP截面上布置若干个数值测点，周向均匀分布的16个点，沿径向布置10个测点，这10个测点是AIP截面上10个等环面的面积中心点，再加上截面中心的1个测点，AIP截面上共布置有161个测点，如图7所示。

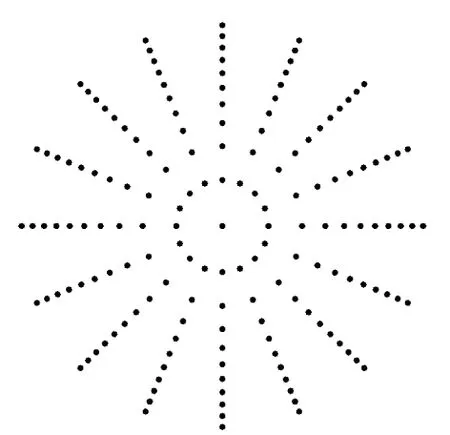
图7 AIP截面测点分布

3.1 固定地板和移动地板计算结果分析

图8为地面固定时不同来流马赫数的反推流场。图中给出了发动机进口和反推出口流线和地面静压云图，图中红色线为流经地面高静压区域流线(如图中红色标记区域)(因本刊为黑白印刷，有疑问之处可咨询作者)。随着来流马赫数的增加，发动机进口捕捉流管直径逐渐减小，反推气流区域也相应缩减，慢慢形成较为规整的反推气流流管。在来流Ma≥0.10时，发动机进口捕捉流管与反推流管在反推力装置前后形成分离的两部分，基本不再相互影响。但是在Ma数较小时，反推气流流管影响区域直径较大，来自反推装置底部叶栅的反推射流在发动机进气唇口前部区域接触地面形成速度滞止区，即高静压区域。在高静压区附近，近地面来流与反推气流相遇，在反推气流和发动机进口捕捉流管的作用下，形成向上气流，来自地面的上升气流(如红色流线示)对捕捉流管底部产生影响。在滑跑速度较小时，如Ma=0.03近地面气流被吸入发动机进口，随着自由来流马赫数的增加，反推气流流管与发动机进口捕捉流管直径减小，反推气流影响区域后移，近地面流线上升趋势减弱，最终趋于一条平直流线带。

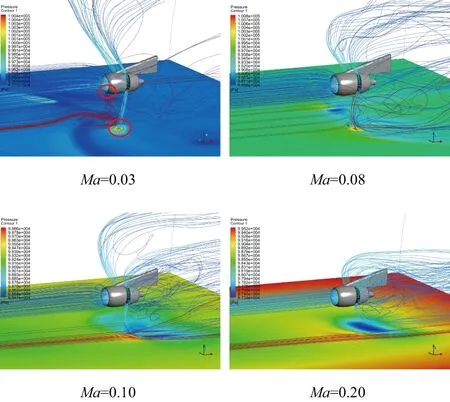
图8 不同Ma数下反推气流扰流流线分布

为了进一步说明地面效应对于发动机进口流场的影响，图9分别给出Ma数分别为0.08、0.22时发动机进口截面总压恢复系数σ分布云图。由图可知，在来流Ma较小时通过给定地面移动速度对由固定地面边界层发展引起的位扰动有抑制作用， AIP截面底部总压损失区缩小；在Ma较大时，两种边界条件计算结果基本一致。由于单发反推流场计算中无机身、机翼等干扰，反推气流无明显直接再吸入现象，由固定地面附面层低能气流被卷吸进入发动机引发的进气畸变，程度小，区域仅在AIP截面底部较为明显。

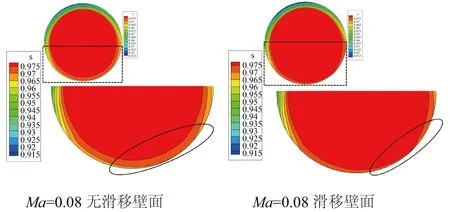
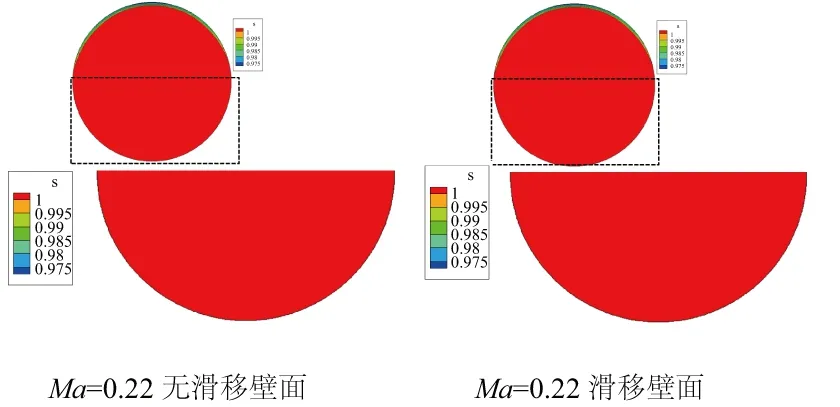
图9 不同马赫数发动机进口截面总压恢复系数σ分布云图

图10分别给出了两种地面边界条件下AIP截面的周向稳态总压畸变指数随来流Ma数变化曲线，由图可知，周向稳态总压畸变指数随相对来流Ma数减小而慢慢增大，大致呈阶梯状，与早年国外学者JOHN H P[13]与HEGEN G H等人[14]通过进口截面温度特征参数表示反推气流对发动机进口的扰动影响结果相似。从图中可以看出，两种壁面边界条件下AIP截面周向稳态总压畸变指数随来流Ma数变化趋势虽然基本一致，但图中线2整体略低于线1，说明移动地板可以达到消除固定地板边界层发展进气的发动机进口底部不均匀性。

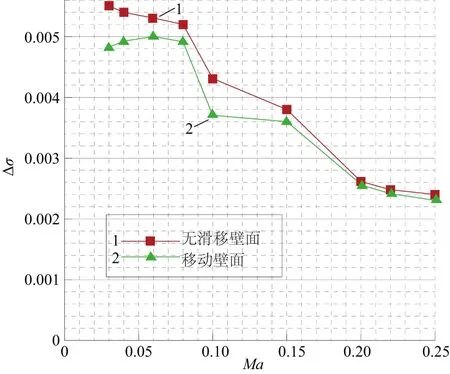
图10 周向稳态总压畸变指数随相对来流Ma数变化曲线

3.2 离地高度影响分析

在前文研究的基础上，选择相对来流Ma=0.08，地面为固定无滑移边界，通过改变H/D大小，开展离地高度对反推状态下发动机进口流场影响研究。

图11给出了发动机进口AIP截面周向稳态总压畸变指数随H/D变化曲线。从图11可以看出，畸变指数随离地高度的降低而减小，到H/D=1.5后，畸变指数又有所增大，最后在0.004 5附近浮动。

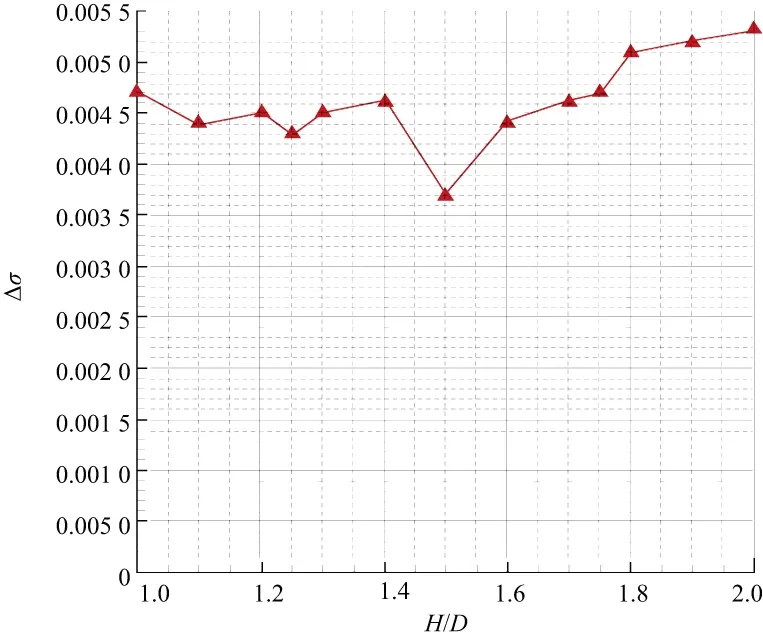
图11 周向稳态总压畸变指数随H/D变化曲线

图12分别给出了H/D=1.2、1.8反推流线和发动机进口流线，地面为静压云图。对比两图可以看出：离地高度的下降使反推气流更早接触地面，高静压区向发动机后部移动，反推流管影响区域减小，降低了对相对来流的卷吸作用，故H/D在1.5～20之间，畸变指数随离地高度的降低而减小；而随着离地高度进一步减小，发动机进口捕捉流管慢慢接触地面，吸入边界层气体，可能造成地面涡吸入，引起发动机进口流场畸变，周向稳态总压畸变增大。

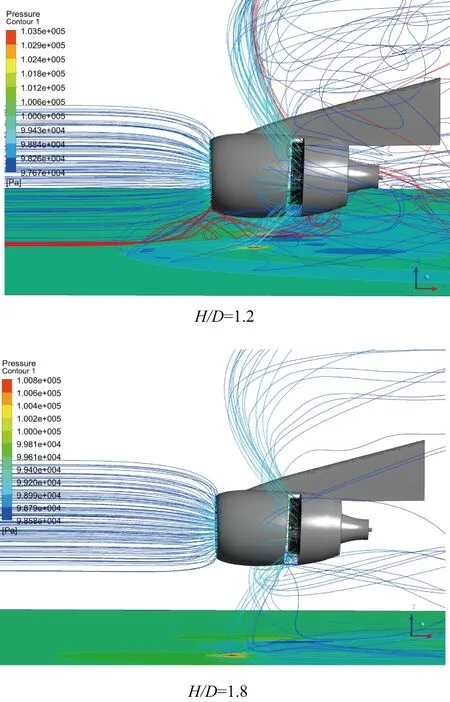
图12 H/D=1.2、1.8反推气流扰流流线分布

4 结语

本文针对反推状态下大涵道比涡扇发动机开展反推扰流流场数值模拟研究，分析地面效应对反推状态下大涵道比涡扇发动机进口流场影响，并通过稳态周向总压畸变随滑跑速度的变化直观展现，为以后相关风洞试验以及大涵道比涡扇发动机设计[15]提供一定的有用信息。