不同拾取端的动态无线电能传输系统研究
刘飞飞,郭波超,任舒琪,朱杨林
(江西理工大学电气工程与自动化学院,赣州 341000)
在20世纪初,特斯拉、Hutin和Leblanc等早期先驱者积极推行无线电能传输WPT(wireless power transfer)研究,此类研究甚至影响现代WPT应用[1]。伴随中国制造2025等国家战略提出,智能工厂[2]、无人仓库及轨道机器人[3]等相关领域也得到更多科研人员的重视,因此对电能传输的便捷性、安全性和美观性提出诸多要求。
互感变化对WPT系统传输效率产生重大影响,已被国内外学者研究与认可。文献[4]通过对电路重新讨论和分析,使用E类功率放大器和整流器保持互感在较高的范围内;文献[5]使用诺以曼公式计算得互感,并利用等效电路模型计算出带有倾斜线圈的WPT系统效率;文献[6]基于傅里叶变换和双傅里叶变换,建立相关模型并对其进行分析计算,得出方形和圆形线圈自感和互感的不同倾向;文献[7]将复杂的多转矩形螺旋线圈转换为单圈矩形线圈,简化了自感与互感的计算;文献[8]提出一种控制方案,既不需知道拾取端的结构参数,便可估计互感系数;文献[9]以常见的矩形截面空心线圈为分析对象,使用诺以曼公式和细分求和法推导互感的理论计算公式,对任意空间位置线圈间互感计算进行研究;文献[10]分析了不同补偿拓扑的互感、负载及效率变化对系统输出的影响,且当互感变化时,系统仍是鲁棒稳定的;文献[11-12]推导WPT系统传输效率与互感的关系式,并对谐振频率、互感系数和线圈内阻等参数之间的关系进行了分析。
在动态无线电能传输系统中,传输效率跟随互感及拾取端的线圈数量改变而变化。相邻发射线圈处在工作状态,其生成的空间磁场将对耦合线圈产生影响。本文通过互感理论对WPT系统进行建模,并分析出互感系数、品质因数、负载及邻近线圈电阻对系统传输效率影响的关系式。通过诺以曼公式求解互感值,并组建实验平台进行验证。最后研究不同形式拾取端,其对系统传输效率的影响。
1 系统模型
动态WPT系统的简易等效电路如图1所示。图中:AC是高频交流电压源,RS是电源内阻,RL是负载,C1、C2、C3和 Ci分别是发射线圈 1、2、3 和拾取线圈的分布电容,L1、L2、L3和 Li分别是发射线圈1、2、3 和拾取线圈的电感,R1、R2、R3和 Ri分别是发射线圈 1、2、3 和拾取线圈的等效电阻,i1、i2、i3和 ii是感应线圈的电流。

图1 动态并联发射端WPT等效电路模型Fig.1 WPT equivalent circuit model of dynamic shunt transmitter
当动态WPT系统的耦合机构发生感应耦合时,等效电路模型的基尔霍夫电压方程和基尔霍夫电流方程分别为
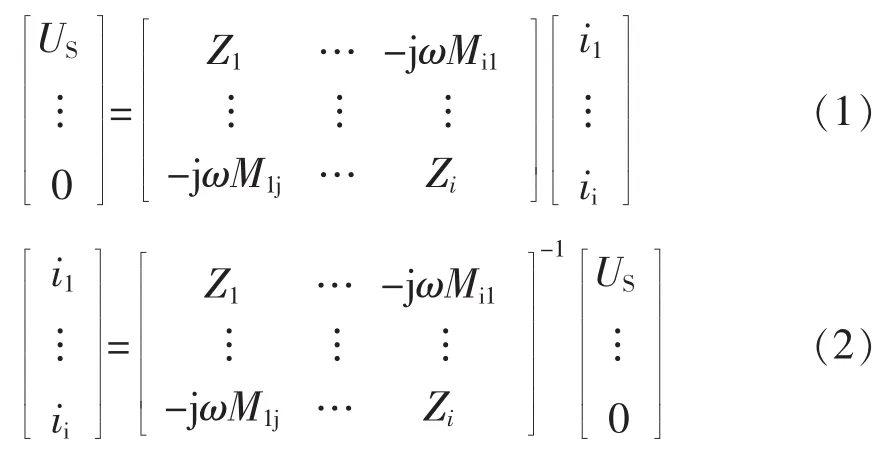
式中:US为线圈中电压 ;ω为系统角频率;M1j为线圈间互感;Zi为线圈的总阻坑,表示为

图2为静止WPT系统的耦合机构在笛卡尔坐标系中径向偏移,图中,r1和r2分别为发射线圈和拾取线圈的半径,θ和φ分为r1、r2与x轴的夹角;dl1、dl2分别为 r1、r2的切线,t为发射线圈和拾取线圈的径向移动距离,h为轴向距离。
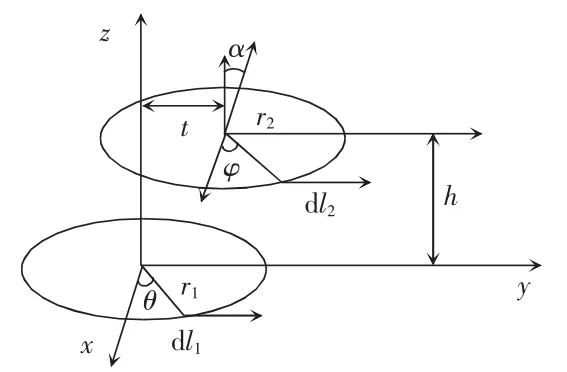
图2 单感应线圈径向偏移Fig.2 Radial offset of single induction coil
根据图2,由诺以曼公式可得耦合机构之间的互感系数为
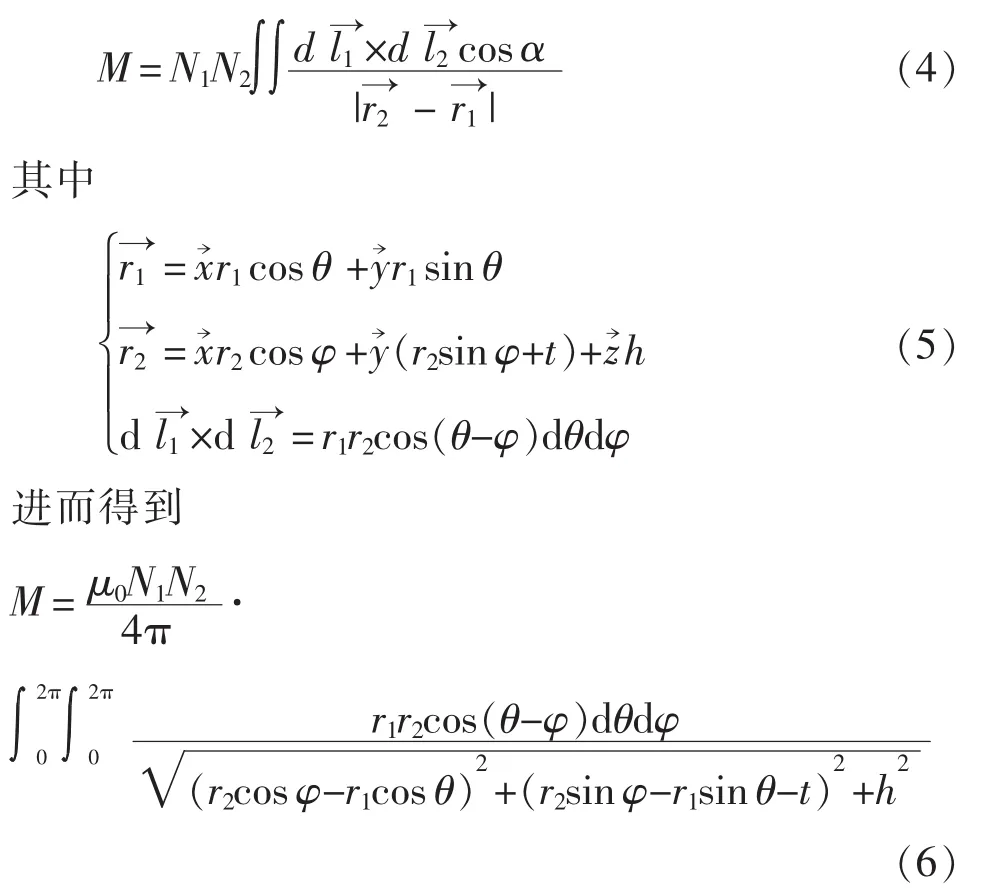
式中:μ0为真空磁导率,μ0=4π×10-7H/m;N1和 N2分别为发射线圈和接收线圈的匝数。
式(6)无法用解析法求解,但可以借助双重积分定义用Matlab求其数值解,设h=0.001 m,r1=r2=0.019 m,单次径向偏移距离为0.001 m,则耦合机构径向偏移的互感变化规律如图3所示。
由图3仿真可见,当t=0.015 m时互感系数已经处于很低的位置,所以发射端之间的耦合仅发生在临近线圈,与拾取端的耦合仅处在相邻两线圈之间。

图3 互感系数径向偏移变化Fig.3 Radial offset of mutual inductance coefficient
当拾取线圈增多,意味着有多组无线电能传输系统在同时工作,但由于各拾取线圈之间有连接,使得线圈的电气参数发生改变,但是不影响互感系数。由式(6)可知,影响互感系数的主要原因有:耦合机构半径r、径向距离和轴向距离[13]。因此,多线圈拾取端的互感系数变化规律仍为图3所示,但是精确计算较为困难,又因为当偏移距离超过线圈的80%时,互感可以忽略不计。
将式(2)简化,得


联立各式,用品质因数和耦合系数来表示绕组中流过的电流,求解得

在得到互感变化规律的基础上,进一步推导输出功率和传输效率。则系统的输出功率为

系统传输效率为

由上述分析可知,系统的输出功率和传输效率与绕组的品质因数、耦合系数、负载和发送端电流有关;品质因数由绕组的阻抗和工作频率共同决定,决定系统的传输效率;而耦合系数决定系统的传输能力,所以本文以品质因数和耦合系数为实验指标,进行验证工作。
2 实验验证
本文通过搭建并联线圈轨道实验平台,探究品质因数和耦合系数的变化对系统输出功率和传输效率的影响。本实验由信号发生器ATTEN ATF40D产生高频信号,通过耦合机构在示波器ATTEN ADS 1102CAL显示能量传输信息,通过功率分析仪PA 6000测量负载功率。
实验所用线圈通过机械绕制,其内经为28 mm,外径为38 mm,线径为0.3 mm×2股,匝数为17匝,并联感应线圈轨道焊制在PCB板上,实验所用负载为10 Ω电阻。线圈的参数通过数字电桥JC2812A LCR测量,其具体参数测量结果如表1所示,实物如图4所示。
所测参数产生偏差的原因有以下3点:①线圈是手工制造的,所以各个线圈之间参数存在差异;②由于焊接工艺不同,线圈电感和电阻发生变化;③铜材料相对较软,容易变形。
由上文可知,线圈品质因数和系统耦合系数对系统传输效率产生影响,因此选用品质系数不同的线圈组建实验平台进行验证,耦合线圈形式分别为单线圈、并联叠加式、并联展开式、串联叠加式和串联展开式,并绘制其变化规律。
图5所示为信号发生器产生的高频信号波形,表示在不同频率下电压峰值Upp和电压有效值Urms的关系。可以看到,在1~3 MHz的频率范围内,产生的峰值电压并没有差异,所以在下文中频率变化时,所产生的其他实验现象主要由频率变化而产生。

表1 各线圈参数测量结果Tab.1 Test results of parameters of each coil

图4 实验线圈Fig.4 Coils used in experiment

图5 不同频率的峰值电压变化Fig.5 Peak voltage variation at different frequencies
在动态充电过程中,发射线圈会根据实际需要以组的形式开断。本文所用实验设备皆已设置成组,探究拾取端在发射线圈组通电情况下的规律变化。
2.1 单线圈耦合机构
图6所示发射端和拾取端为单线圈时的变化规律。图6(a)中的变化规律清晰表明,在没有相邻感应线圈的干扰,传输效率变化趋势与图3所示相同,但在不同工作频率情况下,移动距离在10~20 mm和60~70 mm范围内时存在极小点,而不是与互感变化一致,究其原因是由于发射端产生的磁场并非均匀磁场[14-15],在空间上有疏密之分,正是因为此处为磁场稀疏处,效率出现下跌。在移动至40 mm处时与感应线圈完全重合,但是并非效率最高处,反而是在其两侧出现效率最高,原因同上。然而在1 MHz频率下,在40 mm附近出现极大值,原因是低频磁场疏密差异较小,所造成最大传输效率变化情况与互感系数变化几近相同。上述现象也揭示了在高频磁场下,单感应非致密线圈作为发射端时,拾取端略微偏移对提高系统工作效率有益,并且要在标定工作范围内,如果处在类似于10~20 mm区域,将会损失大量能量。由图6(b)结果可以验证微偏移动使得传输电压升高,进而使得效率增加。图6(c)显示,当增加工作频率,拾取电压并非同频率升高而升高。在设计WPT系统的工作频率时,不应盲目增加工作频率,本文所使用感应线圈工作效率最高频率处在5 MHz附近。对比图6(d)与图5可知,频率升高使传输效率升高,且发射电压与拾取电压为正比关系。
2.2 单线圈拾取端
图7(a)所示为单线圈拾取端在轨道移动时,传输效率的变化,其变化趋势基本与互感系数变化趋势相同,且未出现效率下降现象,原因是轨道发射端产生的空间磁场相互叠加。然而随着系统频率升高,在轨道中心的传输效率并非最高,依然是稍微偏离中心,系统传输效率才是最高。图7(b)也证实在轨道上高工作频率依然存在上述现象,其原因同第3.1节,不再赘述。

图6 单线圈耦合机构的实验结果Fig.6 Experimental results of single-coil coupling mechanism

图7 单线圈拾取端的实验结果Fig.7 Experimental results of pickup end of single-coil
图7与图6的图(c)和(d)的现象变化规律基本一致,但在图7(c)中出现4个极大值点,最大值依然出现在5 MHz附近,与第3.1节中的结论相同。
2.3 并联拾取端
并联拾取端有两种形式:叠加式线圈和展开式线圈,其实验结果分别如图8和图9所示。对比图8(a)与图 9(a)可见,叠加式拾取端最大传输效率优于展开式,但最小传输效率却低于展开式,且以高频率工作时,最大传输效率不在线圈重合处。图8(a)中最大传输效率与最小传输效率差值相对于图9(a)过大,其原因是展开式拾取端在磁场中相对面积较大,而拾取端在移动中抗磁场变化能力优于叠加式,也正因此使得系统无法集中对能量拾取。对比图8(b)与图 9(b),叠加式拾取端依然存在轨道中心并非传输效率最大区域,而是在偏移中心6 mm区域的问题,而展开式拾取端并不存在此现象,其原因与上述相同。

图8 并联叠加式拾取端的实验结果Fig.8 Experimental results of parallel superposition pickup end
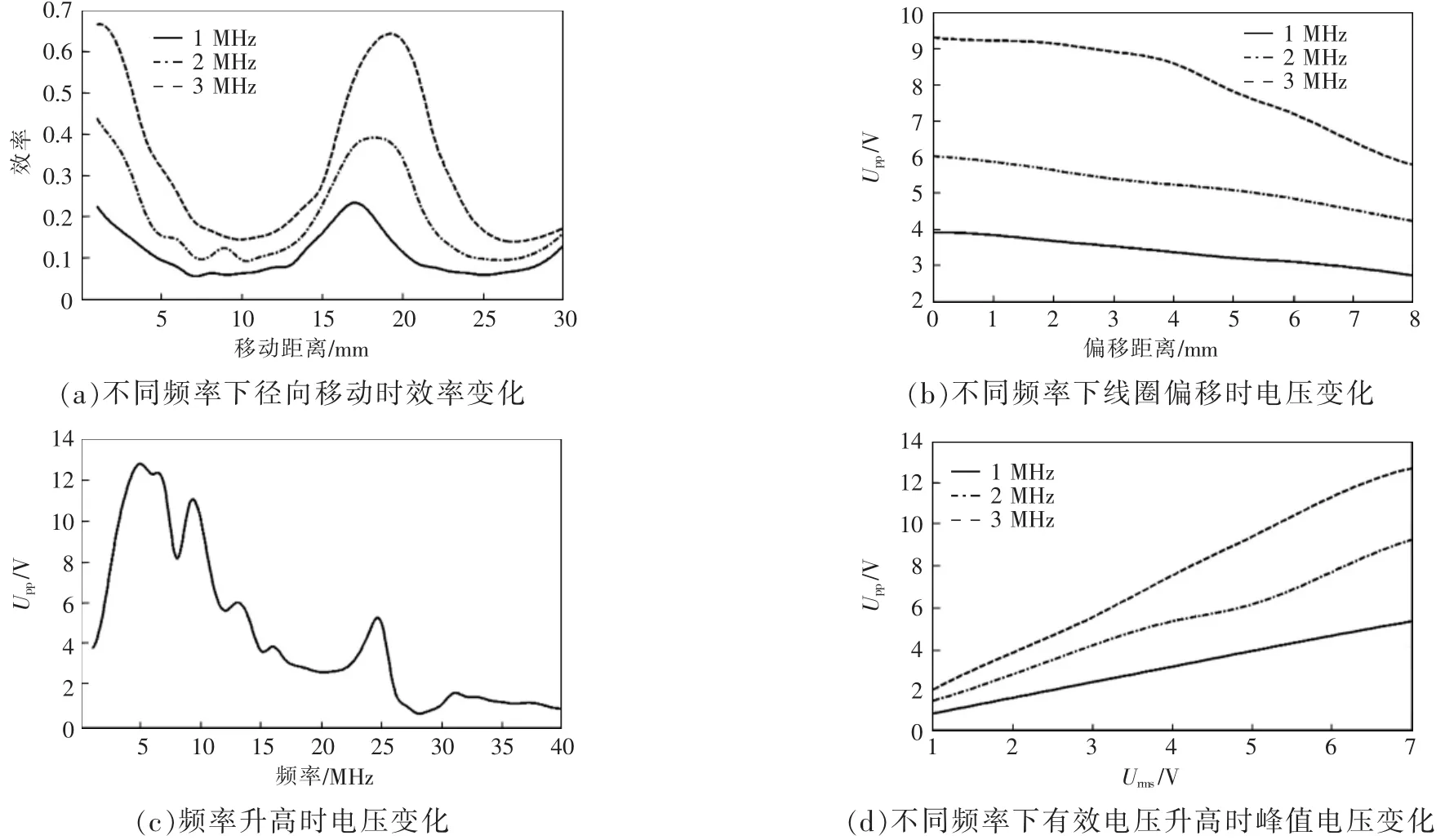
图9 并联展开式拾取端的实验结果Fig.9 Experimental results of parallel expansion pickup end
由式(11)可知,并联式拾取端的电感减小使得拾取端的品质因数下降,造成传输效率降低,所以并联拾取端的总体效率要低于单线圈拾取端。
对比图 8(d)与图 9(d)可知,叠加式的最大传输功率优于展开式的,但其稳定性不好,在拾取端移动或发射端电压变化中都存在突变现象。
2.4 串联拾取端
串联式拾取端也有2种物理形式:叠加式线圈和展开式线圈,其实验结果分别如图10和图11所示。由图 10(a)与图 11(a)可见,两者最大传输效率均不处于同一水平,叠加式最大传输效率在50 mm处,展开式最大传输效率在30 mm处,均处在轨道中间,而且极大值之间相差大约0.05,差值较小,本文认定效率相同。在两者最大传输效率处并未出现图6(a)和图 7(a)的偏移动电压升高的现象,由式(10)可知,串联电感增加,互感系数变小,系统拾取能力下降。图10(b)和图11(b)也证实上述分析。

图10 串联叠加式拾取端的实验结果Fig.10 Experimental results of series superposition pickup end
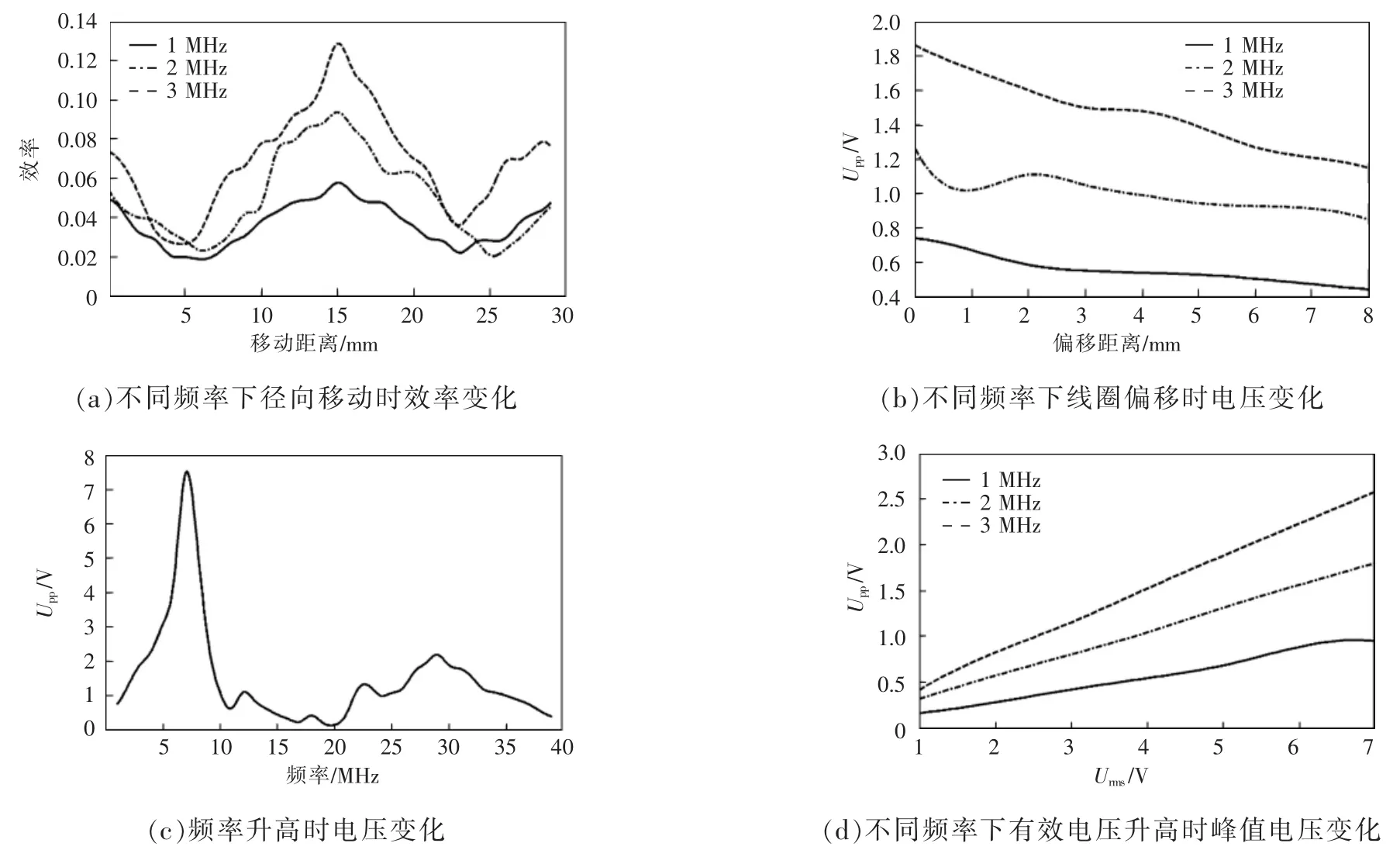
图11 串联展开式拾取端的实验结果Fig.11 Experimental results of series expansion pickup end
串联拾取端最大的问题在于传输效率过低,均处在0.2效率以下,能量损失较多。通过式(8)可知,当感应线圈为串联形式时,感应线圈的电阻增大,使得品质因数和耦合因数都下降,造成效率降低。
图 10(c)、(d)和图 11(c)、(d)对比证明,串联拾取端的电压低于其他形式,原因与上述相同。但在图10(c)中最高电压出现在10 MHz附近,原因是耦合因数变小,使得线圈耦合能力下降。而图11(c)在7 MHz出现最大值,是线圈相对耦合面积较叠加式大,所以互感系数变大,导致耦合系数增加。
3 结语
本文基于互感理论对动态WPT系统进行建模,系统的传输效率与负载电流和负载呈正相关,与电源电压和发射端电流呈负相关。但发射端线圈之间相互耦合,造成发射端线圈电流受到其品质因数Q、耦合系数k、邻近线圈电阻及负载的影响。因为各参数与传输效率是非线性关系,因此会使拾取端在移动过程中传输效率的突然升高或者降低,这是耦合系数改变造成的。由于耦合情况的复杂性,所以无法通过仿真进行定量分析,所以通过实验比对,仅从效率考虑,单线圈拾取端是最好的选择,但是负载电压小于并联叠加式,对于高电压要求的系统,在牺牲一定效率的情况下选择并联式最好。在并联叠加式中,展开式比叠加式的传输效率波动较小,且在较高工作频率系统中传输电压也要高于叠加式的。串联式拾取端在各方面都不及其他形式,对于动态WPT系统不建议采用。由于本文所做实验均基于小功率系统,并未对大功率系统进行验证,略有不足,但对于动态WPT系统轨道设计仍有一定参考意义。

