一种高偏移容限的无线电能传输系统设计
张朱浩伯 ,徐德鸿 ,PHILIP T.Krein,马 皓
(1.浙江大学电气工程学院,杭州 310027;2.浙江大学伊利诺伊大学厄巴纳香槟校区联合学院,海宁 314400)
电动汽车由于其环保、节能、绿色的特性而受到广泛关注,具有良好的应用前景。相较传统的接触式充电,无线电能传输技术由于安全系数更高、能源清洁和充电便捷等优点,可以提供更安全的充电环境,因此成为未来电动汽车能量供给的发展趋势[1-7]。
对于电动汽车的无线充电应用,泊车的随机性会导致耦合变压器的原副边存在一定偏移,该偏移量的增加会引起耦合系数的降低和功率传递特性的显著变化,进而导致充电效率的明显下降。因此,偏移容限特性是无线电能传输系统设计中的关键问题。传统的松散耦合变压器结构,如圆盘型、方型、DD型以及螺线管型等线圈结构,都存在不同偏移方向下耦合系数大幅下降的特性,即在某一偏移方向下存在系统的耦合零点[8-10]。针对上述偏移条件下的容限问题,DDQ和BPP型线圈结构的提出可以扩大偏移范围[11-12]。以DD-DDQ型线圈结构为例,该结构利用副边的DD和Q线圈在不同偏移条件下耦合互补的特性来提高偏移条件下的耦合系数,但是该设计在正对条件下只有DD线圈工作,而在一定的偏移条件下只有Q线圈工作,未能充分利用多个线圈同时实现能量传递。对于多副边线圈结构的变压器,如何充分利用每个线圈的耦合系数为本文研究的重点。另外,由于耦合变压器存在较大的漏感,因此需要对线圈电感进行补偿来提高系统的传输功率和效率。对于多副边线圈结构的变压器,需要在传统的单电容补偿(S/P)以及高阶补偿设计(LCL/LCC)[13-15]中选择合适的补偿方案,通过谐振网络阻抗特性分析,与变压器的耦合特性相结合,从而得到所需要的电路输出特性。
本文提出了一种具有高偏移容限特性的无线电能传输系统设计方法,针对原边螺线管结构、副边双解耦绕组结构的变压器设计,通过理论和仿真分析验证其具有良好的抗偏移特性[16]。另外,针对不同的原副边补偿网络以及整流桥的连接方式,本文给出了电路拓扑的匹配条件,使系统能够充分利用变压器线圈在偏移下耦合互补的特性。最后,通过实验对上述系统设计进行验证。
1 高偏移容限耦合变压器的设计
1.1 耦合变压器结构设计
本文提出了一种高偏移容限耦合变压器结构,如图1所示。其中变压器原边采用的是螺线管结构[11],包括铁氧体磁芯、线圈绕组1和屏蔽铝板;变压器副边采用的是双解耦线圈结构[12],包括铁氧体磁芯、线圈绕组2和3以及屏蔽铝板,其中副边的铝板为了显示变压器的结构而在图1中隐藏掉。副边双线圈分别接收从螺线管线圈传输来的磁场能量。在绕组背面放置的条形铁氧体磁芯可以实现更高的磁通高度,从而增强变压器的耦合特性。

图1 高偏移容限耦合变压器结构Fig.1 Structure of coupled transformer with high misalignment tolerance
对于副边绕组2和3,若2个单面绕组之间存在交叉耦合,则相互之间会传递能量,在电路上表现为高频环流,这增加了系统的损耗并且影响电路的增益特性,因此需要将副边的2个绕组之间进行解耦设计。通常,解耦的方法是调节2个绕组之间的重叠面积,如图2所示,通过调整2个线圈之间的交叠长度,使得绕组2或3产生的磁通在另一个线圈上的交链和为0,即穿入磁通Φ1和穿出磁通Φ2大小相同、方向相反。因此在理想情况下,一个绕组上的高频电流不会在另一个绕组上产生感应电压。
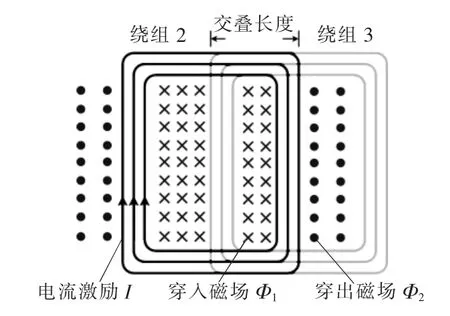
图2 副边线圈绕组2和3的解耦设计Fig.2 Decoupling design of secondary coil windings 2 and 3
基于上述结构,在600 mm×600 mm的变压器尺寸以及200 mm气隙间距的条件下,通过Ansys Maxwell 3D有限元软件对变压器的参数进行仿真和优化。其中,为了降低系统成本与重量,采用6个条形的铁氧体磁芯作为导磁路径,每条均由60 mm×35 mm×12 mm尺寸的磁芯拼接而成。另外,考虑到无线电能传输系统的额定工作频率为85 kHz,因此变压器线圈选择由0.1 mm×400的利兹线绕制而成。通过参数化仿真的方式,可以得到在上述条件下磁芯间距、原边螺线管的线圈宽度以及副边双解耦绕组线圈宽度的优化值,以实现更高的耦合系数。本文所设计的耦合变压器的具体结构尺寸如图3所示。此外,在实际的变压器制作中,铝板、磁芯以及线圈之间均添加了2 mm的环氧树脂板,以起到绝缘和支撑的作用。

图3 耦合变压器结构尺寸标注Fig.3 Dimensional diagram of coupled transformer structure
1.2 耦合变压器结构仿真分析
相较于原边采用DD型的线圈结构,螺线管型线圈结构可以产生更高的磁通高度,在相同传输距离的条件下可以使变压器达到更高的耦合系数[11],有利于系统在偏移条件下仍维持较高的耦合水平,从而增强系统在正对以及偏移下的功率传输能力。结合螺线管绕组结构磁通高度更高的优点以及双解耦绕组结构在不同偏移条件下互补的耦合特性,上述变压器结构可以实现更高的偏移范围。在不同的偏移距离条件下,变压器的耦合系数可以根据上述有限元仿真模型得到,其相应的变化曲线如图4所示。其中,变量k12、k13分别代表线圈绕组1和2、线圈绕组1和3之间的耦合系数,变量k代表k12和k13之和。由于变压器的结构具有轴对称以及中心对称的特性,因此只需考虑沿着X轴和Y轴正方向的偏移特性,可由对称性得到其他方向相应的耦合特性。

图4 耦合变压器的偏移特性仿真结果Fig.4 Simulation results of misalignment characteristics of coupled transformer
在沿X轴正方向即沿着磁通路径的偏移方向上,线圈绕组2逐渐远离螺线管线圈的中轴线,线圈绕组3则先靠近再远离该中轴线。当绕组恰好位于中轴线上时,原边线圈在其上产生的净磁通为0,因此耦合系数为0。如图4(a)所示,在沿X轴的偏移方向上,耦合系数k13先下降后上升,当偏移距离为150 mm时近似处于零耦合点,另一方面,由于线圈绕组2的位置靠近螺线管线圈的中轴线,因此耦合系数k12先略微上升达到峰值,然后持续下降,针对2个耦合系数不同的变化趋势,两者之和可以在300 mm的偏移范围内保持不低于0.2的耦合水平。如图4(b)所示,在沿Y轴的偏移方向上,线圈绕组2和3具有相同的偏移特性,其耦合系数之和在300 mm的偏移范围内也保持不低于0.2的耦合水平。如图4(c)所示,在沿X轴和Y轴的对角线斜方向上,耦合系数k12和k13的变化趋势为沿X轴与Y轴方向上对应耦合系数的变化趋势叠加作用的结果,其中横坐标轴代表的是沿X轴和Y轴方向同时偏移0~300 mm。值得注意的是,上述仿真结果中给出的是各个耦合系数的绝对值,其等效于电路拓扑上整流桥的作用,具体的电路拓扑匹配关系将在本文第2节中加以说明。
从磁场分布的角度分析在偏移条件下原副边线圈的耦合情况,正对和沿X轴方向150 mm偏移条件下的耦合变压器截面磁场分布如图5所示。

图5 耦合变压器截面磁场分布Fig.5 Cross-sectional magnetic field distribution of coupled transformer
在正对条件下,原边线圈产生的主磁通向上穿过绕组3、向下穿过绕组2,2个副边绕组的耦合磁场强度相同,但方向相反。在发生X轴方向的偏移时,绕组2与绕组1之间的净耦合磁通逐渐减小。在150 mm的偏移条件下,绕组2与绕组1之间出现幅值相同、方向相反的磁通,因此两者之间的耦合近似为0。随着偏移量的继续增大,该净耦合磁通向相反的方向逐渐增大。在相应的X轴偏移条件下,绕组3与绕组1之间的耦合磁场方向则始终保持不变。而对于沿Y轴偏移方向,2个副边线圈处于等价的地位,因此磁通变化特性相同。上述基于耦合磁场的分析与图4的仿真结果相符,这有利于系统在整个偏移范围内实现功率的高效传输。另外,副边线圈的交叉互感在整个偏移条件下始终保持在较低水平,其耦合系数均低于0.03,因此对于谐振补偿网络的影响较小。
2 电路拓扑设计
本节基于上述耦合变压器的结构特性给出相应电路拓扑的设计条件。在原边螺线管、副边双解耦绕组结构的基础上,电路拓扑共有3个自由度可以调整:变压器原边的补偿网络、变压器副边的补偿网络以及整流桥输出侧的能量叠加方式。其中针对大功率电动汽车无线电能传输系统的特点,相应的电路设计应满足下述2个条件:
(1)对于变压器的补偿网络,为了降低系统阶数,常用的有单电容串联(S)或并联(P)以及 LCL型的补偿拓扑,但是由于系统的输入或输出直流母线通常为电压源特性,若采用电容并联的补偿方式,则逆变器输出或整流桥输入侧方波电压的上升沿或下降沿会在该电容支路上产生较大的瞬态电流,增加电容的耐受量,并且影响电路的稳定运行,因此该补偿方式通常搭配电感形成LCL网络。
(2)变压器副边绕组接收到的能量可通过交流侧或直流侧进行叠加,但是考虑到交流侧功率叠加所需的锁相功能对精度要求较高,所需控制电路较为复杂,因此一般选择在直流侧叠加的方法,即在整流桥后进行功率叠加。
基于上述分析,变压器的原边和副边均可采用单电容串联或者LCL型的补偿网络,同时直流输出侧可以采用电路并联或者串联的方式进行功率叠加,经过排列组合共有8种拓扑。但是,这8种电路拓扑并不都能与所设计的变压器特性相符合,电路特性也各不相同。与变压器结构相匹配的电路拓扑适用条件如图6和图7所示,变压器的原副边均为单电容串联的补偿方式,但是直流输出侧分别以串联和并联方式相连接。

图6 原副边串联补偿且输出串联电路拓扑Fig.6 Circuit topology with S-S compensation and serial output

图7 原副边串联补偿且输出并联电路拓扑Fig.7 Circuit topology with S-S compensation and parallel output
由基波分析法,可以得到下述电路特性的建模与分析。由于副边线圈分别接收原边线圈传输的能量,因此2个副边线圈上的感应电压分别为

式中:Lp为原边侧线圈自感;Ls1和Ls2分别为副边侧双线圈每个线圈的自感;M12和M13分别为原边侧线圈与副边双线圈的互感。
系统的谐振条件为
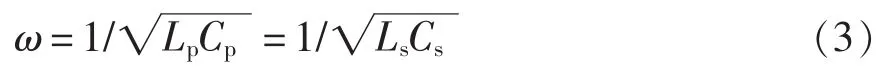
式中:Ls和Cs分别为2个副边解耦线圈绕组的感量以及相应的补偿电容值,且Ls=Cs;Lp和Cp分别为原边侧线圈和相应的补偿电容值。由于2个副边线圈为解耦设计,副边两路之间不会产生相互影响,因此,对于图6所示的直流输出侧串联的电路拓扑,电路的输出电压[17]可以表示为


因此,该电路拓扑的电压增益表达式为
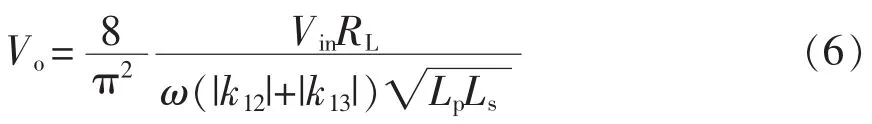
由于整流桥的存在,无论原副边线圈之间的磁通交链方向是否相同,即无论耦合系数k12和k13是否同号,均不影响电路的输出特性,因此式(4)和式(6)中用绝对值符号表示耦合系数对电路的影响。2个耦合系数绝对值之和也正好与本文第2节中给出的变压器的耦合特性相符。另外,从式(6)中可以得到,对于图6所示的电路,其输出特性为1个恒流源,即在谐振条件下电路的输出电流值不因负载电阻的变化而变化。相对应的,对于图7所示的输出并联的电路拓扑,其满足

该电路拓扑的输出电流为两路副边整流桥的输出电流之和,但是,两路电流与相应的2个耦合系数之间不存在线性的对应关系。另外,磁场传递能量的过程均为高频电流通过磁链在线圈中产生感应电压,因此该电路拓扑相当于2个副边的感应电压通过2个整流桥相并联。当两路耦合系数不相等时,电压源的并联会导致内部的环流,影响电路的正常运行,与变压器特性不相符。
在图6所示电路的基础上,若变压器的原边改为LCL型补偿结构,则电路整体表现为电压源特性。如图8所示,此时系统的谐振条件仍为式(3),其中原边的补偿电感值等于原边线圈电感,均用Lp表示。LCL型电路结构可以起到将交流电流和交流电压相互转换的作用,其转换关系式可由诺顿定理得出。对于如图8所示的电路,在式(4)的基础上可以得到电路输出关系表达式为

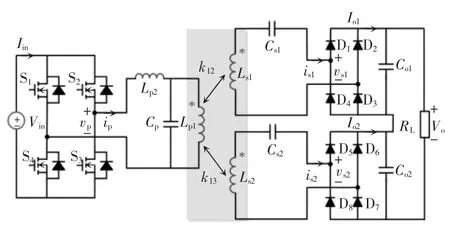
图8 原边LCL、副边串联补偿且输出串联电路拓扑Fig.8 Circuit topology with LCL-S compensation and serial output
根据上述分析,对于副边采用串联补偿的电路拓扑,应采用整流桥输出侧串联的方式实现与耦合变压器的特性匹配;而对于副边采用LCL型补偿的电路,其电路特性则截然相反。
图9所示为原边串联、副边LCL型补偿且输出侧并联的电路拓扑。同样通过诺顿定理,可以建立整流桥前的交流电流和副边线圈上感应电压之间的关系,即
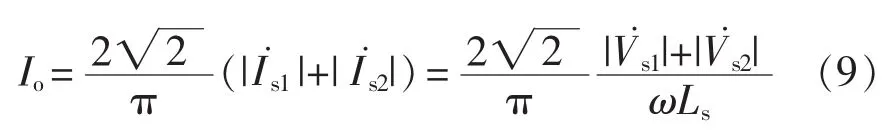
同样,根据式(5)的功率守恒条件,可以得到该电路拓扑的电压增益表达式为

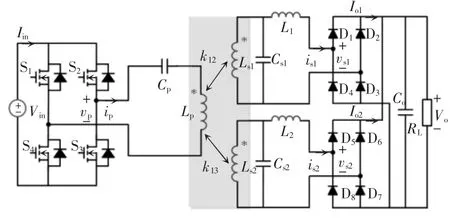
图9 原边串联、副边LCL补偿且输出并联电路拓扑Fig.9 Circuit topology with S-LCL compensation and parallel output
因此该电路的输出特性为一个恒压源。同理,若电路副边为LCL型补偿网络且整流桥输出为串联连接,则会遇到与图7分析中相同的问题,即整流桥的两路电压值无法与相应的2个耦合系数之间建立线性的对应关系。另外,副边2个线圈上的感应电压通过LCL型补偿网络转换为电流值,整流桥的串联则相当于2个电流源的串联,这同样会影响电路的正常运行,与变压器特性不相符。
原、副边均采用LCL型补偿电路的拓扑,如图10所示,在式(9)的基础上可以得到恒流源关系表达式为
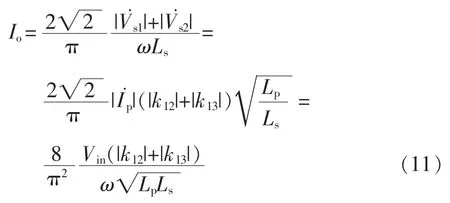

图10 原、副边LCL补偿且输出并联电路拓扑Fig.10 Circuit topology with LCL-LCL compensation and parallel output
综上所述,通过排列组合得到的8种电路拓扑方案中,能与所提耦合变压器结构配合使用的只有其中4种,并且这4种拓扑分别表现出不同的电路特性,其性能比较如表1所示。
另外,将双路解耦线圈放置在变压器原边,并且将螺线管线圈放置在副边也是一个对偶的方案。该方案因如下2点原因而不推荐使用:第一,该方案需要原边两组逆变器模块作为2个独立源使用,增加了系统成本;第二,为了配合变压器特性,2个逆变器需要根据变压器的耦合情况选择开通时序,即选择同步开通或错位180°开通,这对于电路的控制逻辑提出了更高的要求。因此,表1所示的4种方案是考虑到系统成本与性能的较优选择。

表1 与耦合变压器相匹配的4种电路拓扑比较Tab.1 Comparison among four circuit topologies matched with the coupled transformer
3 实验验证
为了验证本文所提耦合变压器以及电路拓扑的特性,选择原边串联、副边LCL且整流桥输出并联的电路拓扑进行实验验证,其电路拓扑如图9所示,搭建的实验平台如图11所示,相应的平台设计参数如表2所示。其中,主功率电路由耦合变压器、原边高频逆变器、副边两路整流桥以及相应的补偿谐振电容和电感组成。变压器原边逆变器选用IPW65R080CFD型号的MOSFET,变压器副边的整流桥选用IDW16G65C5型号的二极管。变压器副边电路的电压信号通过副边的DSP控制器进行采样,并由蓝牙模块传输至原边,从而由原边的DSP控制器产生逆变器的驱动波形。对于耦合变压器,严格按照仿真模型的尺寸进行制作。另外,为了实现原边逆变器开关管的软开关,采用增加原边补偿电感值的方法调整谐振参数,使逆变器的输出阻抗呈现为弱感性。

图11 实验样机平台以及耦合变压器实物Fig.11 Experimental prototype platform and coupled transformer
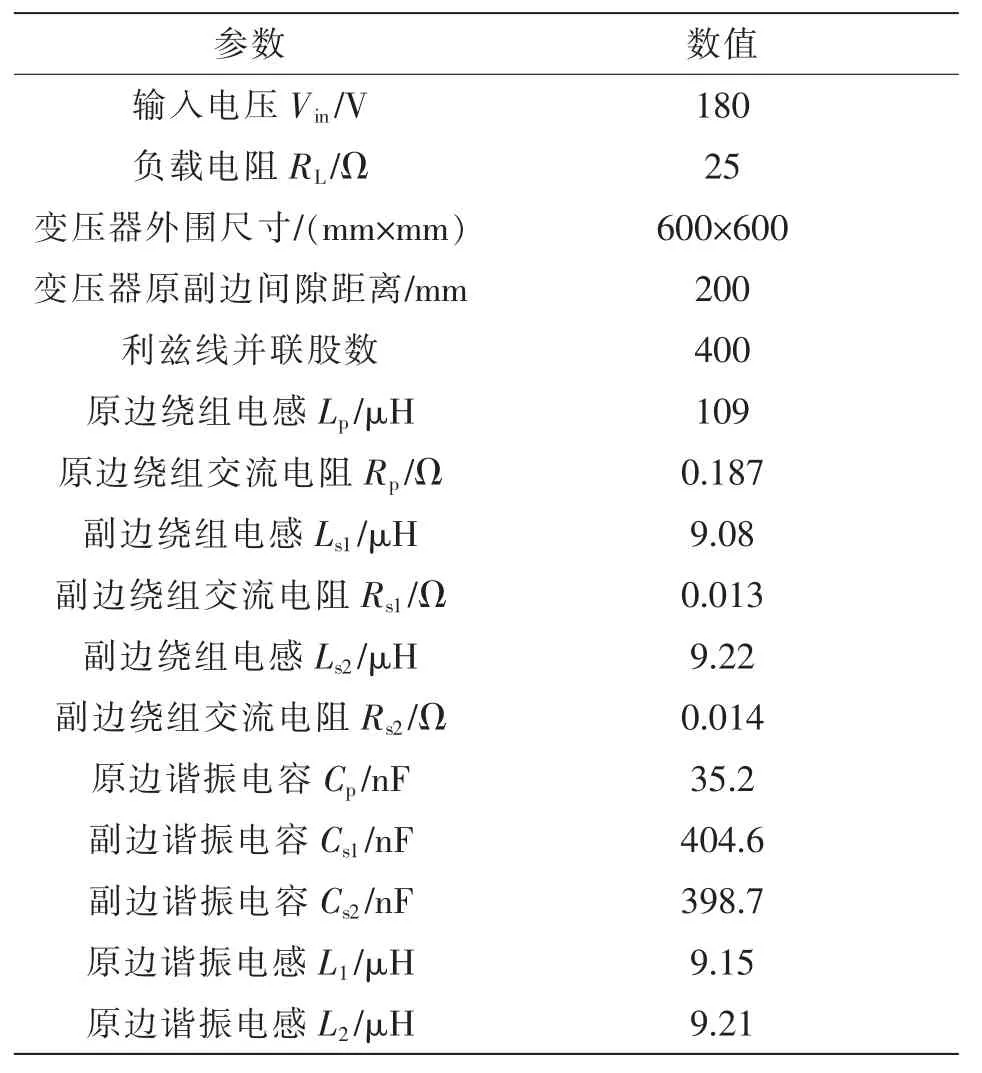
表2 实验平台设计参数Tab.2 Design parameters of experimental platform
首先用LCR表分别测出原边绕组与副边双绕组之间的耦合系数在不同偏移条件下的变化情况,其测试点位置以及相应的测试结果分别如图12和图13所示。图13中关于沿X轴方向偏移、沿Y轴方向偏移以及沿X/Y轴对角线方向偏移的测试结果与图4中的仿真结果基本吻合。在沿X轴和Y轴300 mm的偏移方向上,双解耦绕组线圈的耦合系数之和大体保持在高于0.2的水平,该实验结果验证了仿真模型的准确性。
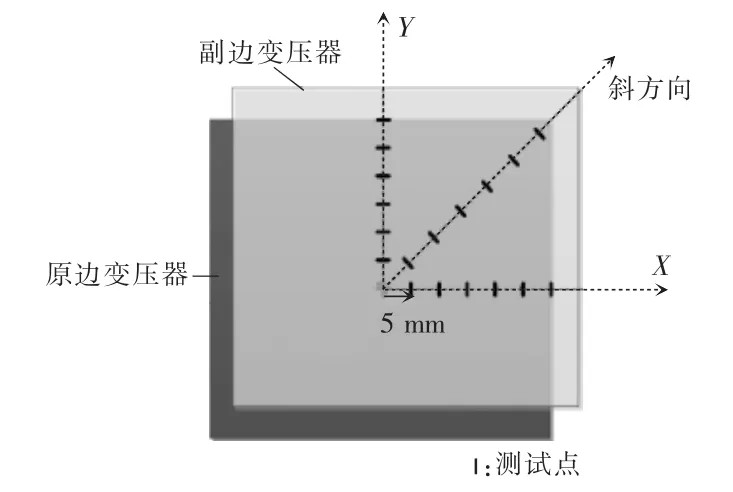
图12 耦合系数测试点示意Fig.12 Testing points for coupling coefficients

图13 耦合变压器的偏移特性实验结果Fig.13 Experimental results of the misalignment characteristics of coupled transformer
测试系统在正对以及偏移条件下的电路特性。图14~图16所示为耦合变压器在正对、沿X轴偏移150 mm以及250 mm条件下,逆变器输出电压vp以及变压器副边两路输出电流is1和is2的实验波形。由图可以看出,随着偏移量的增加,副边电流is1先减少后增加,而副边电流is2则先增加后减少。当原副边正对时,副边两路电流幅值相等,相位相差180°;当偏移量为150 mm时,其中一路由于耦合系数为0,因此相应的电流也近似为0;当偏移量为250 mm时,两路副边电流幅值近似相同,相位同相,这与上文中的理论分析结果相吻合。
图17给出在不同偏移条件下的系统效率特性,可见,当变压器的原副边正对时,系统达到95.2%的最高效率,当偏移到150 mm和250 mm时,系统效率下降到92.2%。
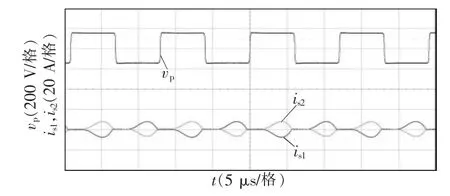
图14 耦合变压器正对时的实验波形Fig.14 Experimental waveforms of coupled transformer without misalignment
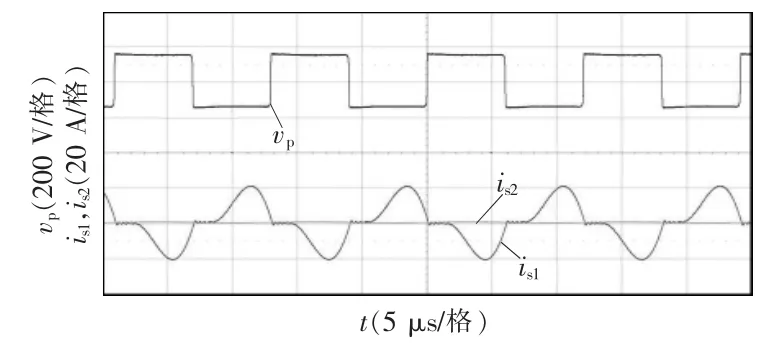
图15 耦合变压器沿X轴偏移150mm时的实验波形Fig.15 Experimental waveforms of coupled transformer with 150 mm lateral misalignment

图16 耦合变压器沿X轴偏移250mm时的实验波形Fig.16 Experimental waveforms of coupled transformer with 250 mm lateral misalignment

图17 耦合变压器在正对以及偏移下的效率特性Fig.17 Efficiency characteristics of coupled transformer with and without misalignment
4 结语
电动汽车在停泊时的偏移容限问题是无线充电系统应用中的关键难题。本文提出了一种原边螺线管、副边双解耦绕组的变压器结构,通过理论和仿真分析验证了其具有良好的偏移特性。另外,针对不同的原副边补偿拓扑网络以及整流桥的连接方式,本文给出了相应的拓扑匹配条件,从而能与所提出的耦合变压器配合使用,充分利用了变压器线圈在偏移下耦合互补的特点。最后,通过实验验证了系统设计的有效性。

