飞翼布局无人机控制律设计

张羽白， 肖成方， 邹俊俊， 翁雪花

(航空工业江西洪都航空工业集团有限责任公司，江西 南昌 330024)

无人机机动航迹的跟踪和控制是其完成各项飞行任务的前提，对于要求能够自主飞行的无人机而言，实现飞行航迹的精确控制尤其重要。飞控系统控制律设计与飞行品质及飞行性能密切相关，是保证系统功能和飞机飞行品质的最直接、最重要的关键环节。

国内外对此进行了广泛而深入的研究，提出了各种飞行控制律设计的方法，如最优控制、自适应控制、鲁棒控制、变结构控制、模糊控制和神经网络控制等。近年来，非线性动态逆以及基于动态逆的μ综合方法、神经网络补偿逆误差方法等已开始在飞机自动飞行控制律的设计中得到应用，但由于这些方法均有不够完善之处，目前在工程中得到实际应用的尚属少数。在工程实践中使用经典PID(比例-积分-微分)控制方法，是国内外发展最早、较为成熟的控制方法之一。本文基于飞机的线性化运动模型进行飞控系统控制律设计，PI控制器各个参数具有明确的物理意义，调整方便、可靠性高。

1 飞翼布局无人机特性

本文中作为控制律设计对象的飞翼布局无人机外形如图1所示，共有3组6个操纵面对称分布，包括内侧升降副翼、外侧升降副翼和开裂式方向舵。

操纵面的功能如下：升降副翼具有纵横向操纵能力，联动偏转可以实现俯仰操纵，差动偏转可以实现滚转操纵，其中内侧升降副翼主要执行纵向控制，外侧升降副翼主要执行横向控制；开裂式方向舵主要产生偏航操纵力矩，执行航向控制；三组舵面均会产生俯仰和滚转耦合效应。

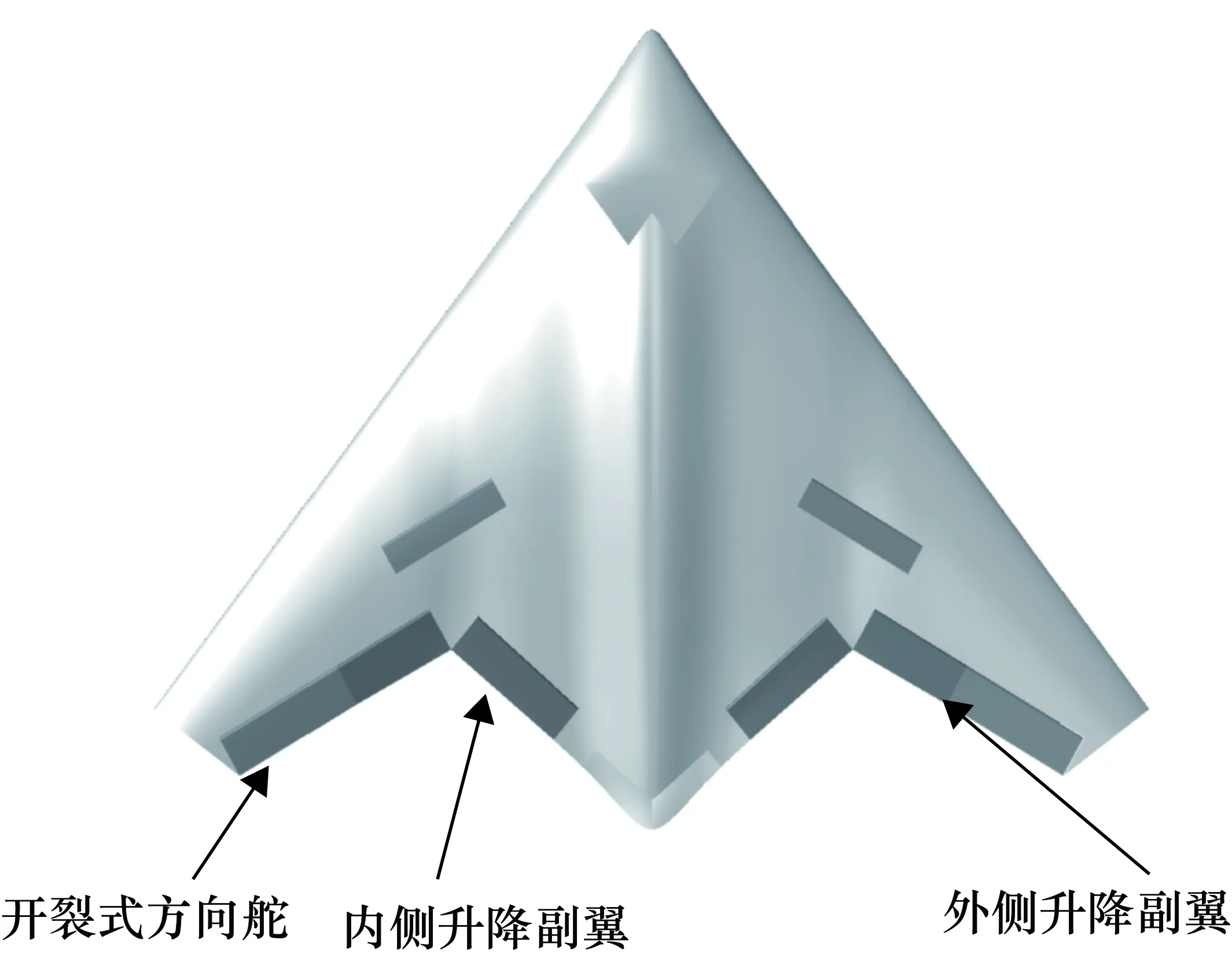
图1 平台模型

飞翼布局无人机的力和力矩模型如下：

(1)

(2)

式中，δie为内侧升降副翼偏角；δoe为外侧升降副翼偏角；δsdr为开裂式方向舵偏角。

飞翼布局无人机的优势为升阻比高、重量轻、RCS低和翼载荷小，但由于没有垂尾和平尾，相比常规布局飞机，气动特性有较大差异，在操稳特性方面存在可控迎角范围小、纵向稳定性差、航向弱静不稳定、几乎可以忽略的侧力导数和三轴弱阻尼等特点。为改善其飞行品质，实现精确导航，纵向和横航向控制增稳设计十分必要。

2 控制律设计思路

现代飞行控制系统控制律总体上是由内回路、外回路和导航回路3个典型回路组成的，如图2所示。内回路实现对飞机飞行品质的改善，如增大阻尼，增强稳定性等，又称为增稳回路；外回路根据导航信息实现姿态角控制及速度控制，所产生的指令信号通过内回路控制飞机的运动；导航回路根据导航任务需求解算姿态角和速度信息给外回路。内、外回路控制律同时协调工作，能够精确控制飞机飞行航迹。

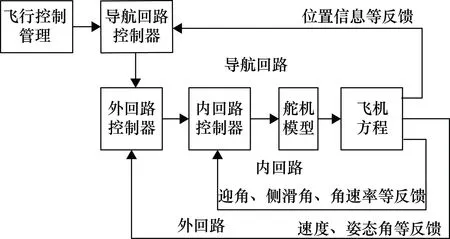
图2 控制律回路示意图

本文着重介绍控制律内回路与外回路的设计，设计及建模仿真验证均在Matlab环境下进行，设计流程如图3所示，设计方法简介如下。

① 梳理飞机气动、质量特性等数据，建立气动力仿真模型。

② 在飞行包线范围内选择若干设计点，进行配平并计算三轴大导数，在平衡点上进行线性化，建立无人机的小扰动运动模型。

③ 计算飞机本体模态特性，根据GJB 185-1986要求确定控制律内回路增稳所需反馈类型，设计内回路控制律结构并调节其增益。

④ 在内回路控制律基础上，根据任务需求设计外回路控制律结构，并对其增益进行调节。所有内、外回路增益均随高度和马赫数调参。

⑤ 针对内、外回路控制律设计结果，按照GJB 185-1986要求进行飞行品质计算，同时按照GJB 2191-1994要求进行导航精度复查和稳定裕度计算检查。

⑥ 建立六自由度仿真模型，验证飞机姿态控制仿真结果满足GJB 2191-1994关于自动驾驶保持精度的要求。

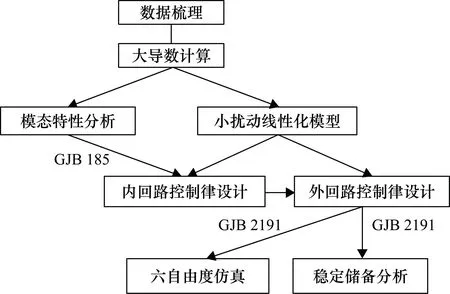
图3 控制律设计流程

3 模态特性分析

选取飞行包线内的典型状态点进行配平并计算大导数，作为研究的基准状态建立线性小扰动模型。

飞翼布局无人机纵向小扰动运动方程的矩阵形式为

(3)

式中,δp为油门。

横航向小扰动运动方程的矩阵形式为

(4)

由于篇幅限制，此处省略大导数计算和模态特性计算，详细计算方法可参考飞机飞行品质计算手册[1]。

3.1 纵向模态特性分析

根据纵向大导数计算飞机本体纵向短周期模态特性，结果如表1所示。

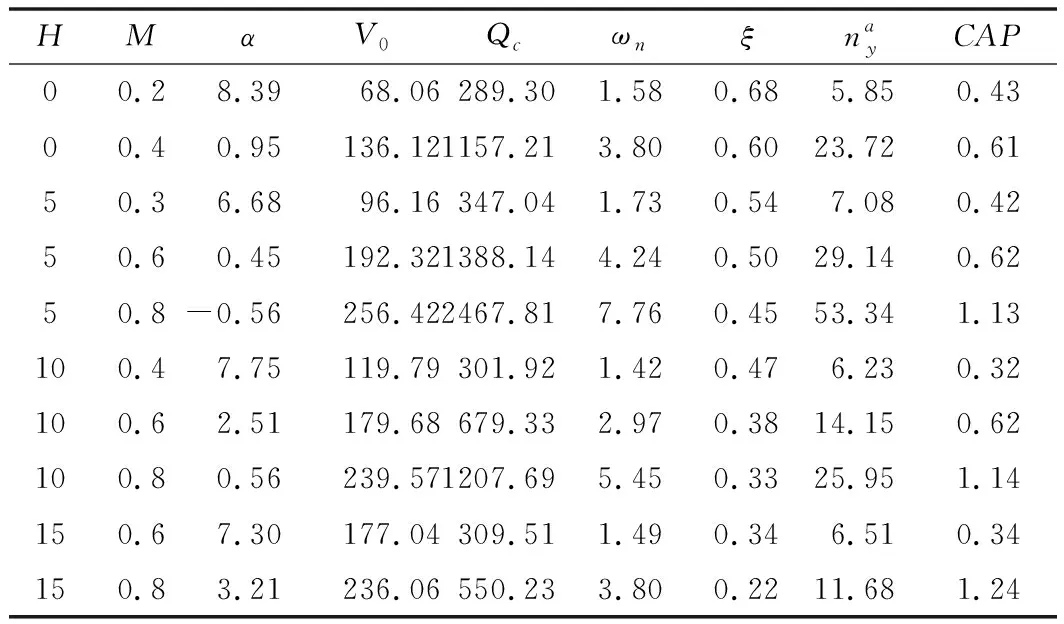
表1 飞机本体纵向短周期模态特性

GJB 185-1986中纵向短周期阻尼比要求如表2所示，操纵期望参数CAP要求标准1在0.28～3.6之间，标准2、标准3在0.16～0.28和3.6～10之间。

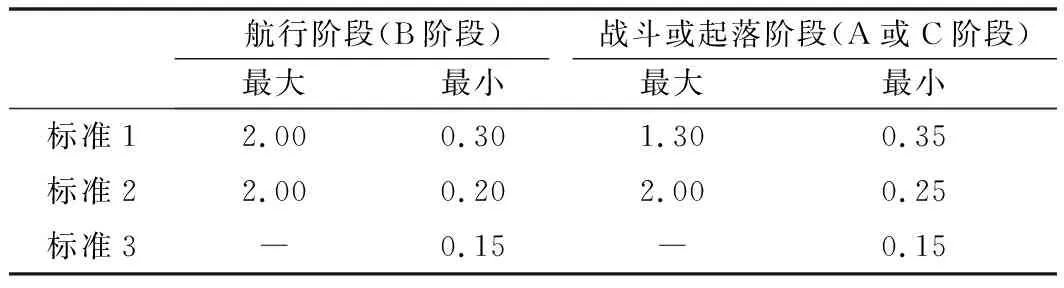
表2 GJB 185-1986短周期阻尼比的限制

由表1分析飞机本体短周期模态特性，阻尼比随高度增加而减小，高空阻尼比偏小，不满足GJB 185-1986标准1要求，操纵期望参数随速度增加而增大，低速时操纵期望参数相对偏小。

3.2 横航向模态特性分析

计算稳定轴系的横航向大导数，并分析其横航向模态特性，结果如表3所示。

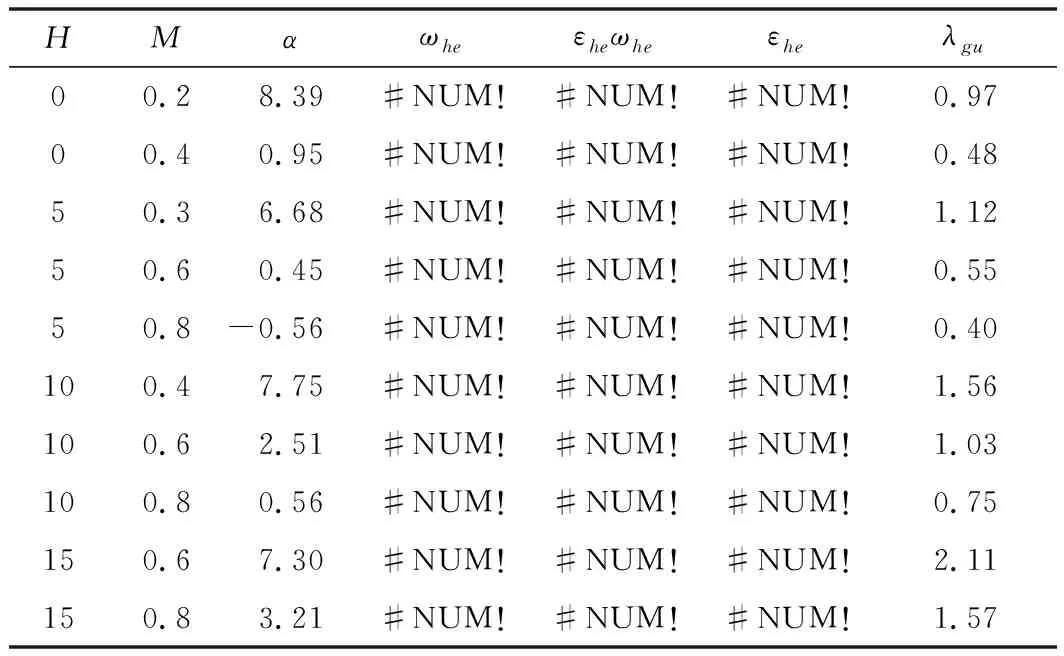
表3 飞机横航向本体模态特性

GJB 185-1986中关于荷兰滚模态特性要求如表4所示，最大滚轮模态时间常数如表5所示，滚转模态时间常数应不大于表5中的相应值。

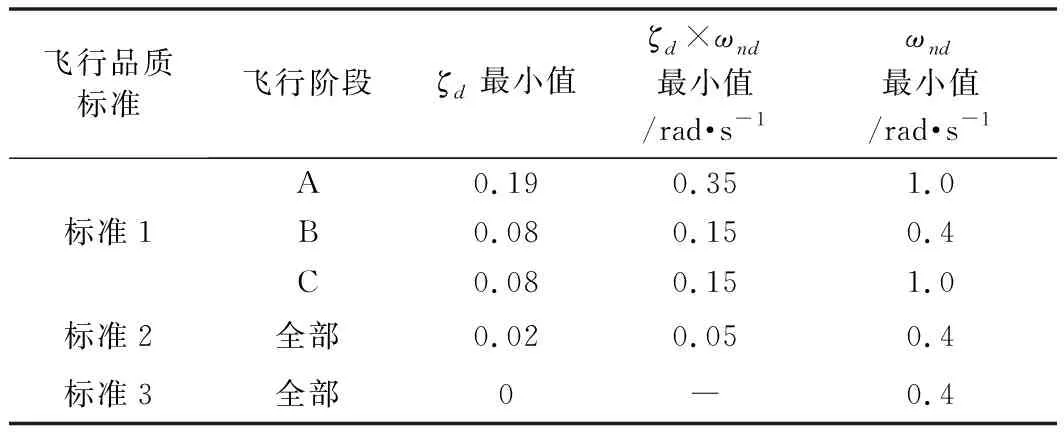
表4 GJB 185-1986荷兰滚模态最小无阻尼自振频率和阻尼比

表5 GJB 185-1986最大滚转模态时间常数 单位：s

分析发现,该无人机航向静稳定性和阻尼不足，横航向荷兰滚模态发散，如不引入反馈改善飞行品质，横航向将无法进行控制。

4 内回路控制律设计

4.1 内回路纵向控制律设计

由纵向小扰动方程可知，纵向全状态反馈为ΔV,Δα,ωz,Δϑ，根据经验分析计算结果，一般情况下速度反馈系数V很小，忽略后可以得到与经典控制理论一致的方法，即通过迎角α反馈保证其纵向静稳定性，通过俯仰角速率ωzt反馈改善短周期阻尼特性，通过俯仰角ϑ反馈抑制长周期沉浮模态。

针对2.1节的飞翼布局无人机纵向模态特性分析结果，为改善飞机动态响应特性，增大短周期阻尼比，内回路中加入俯仰角速率ωzt反馈到舵机输入端，纵向增稳系统结构如图4所示。加入纵向内回路反馈后的舵面偏转规律表达式为

δie=δiec+Kωz×ωzt

(5)

式中，δie为内侧升降副翼控制指令；δiec为纵向外回路控制律信号输出；Kωz为俯仰角速率反馈增益。

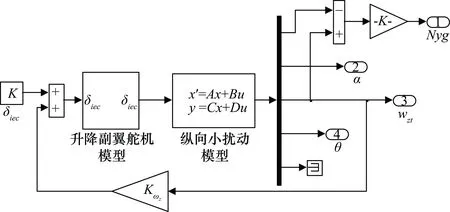
图4 纵向增稳系统结构

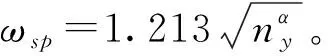
纵向内回路反馈后再次计算纵向短周期特性，近似计算中的使用的当量大导数为

(6)

反馈后的短周期模态特性计算结果如表6和图5所示。

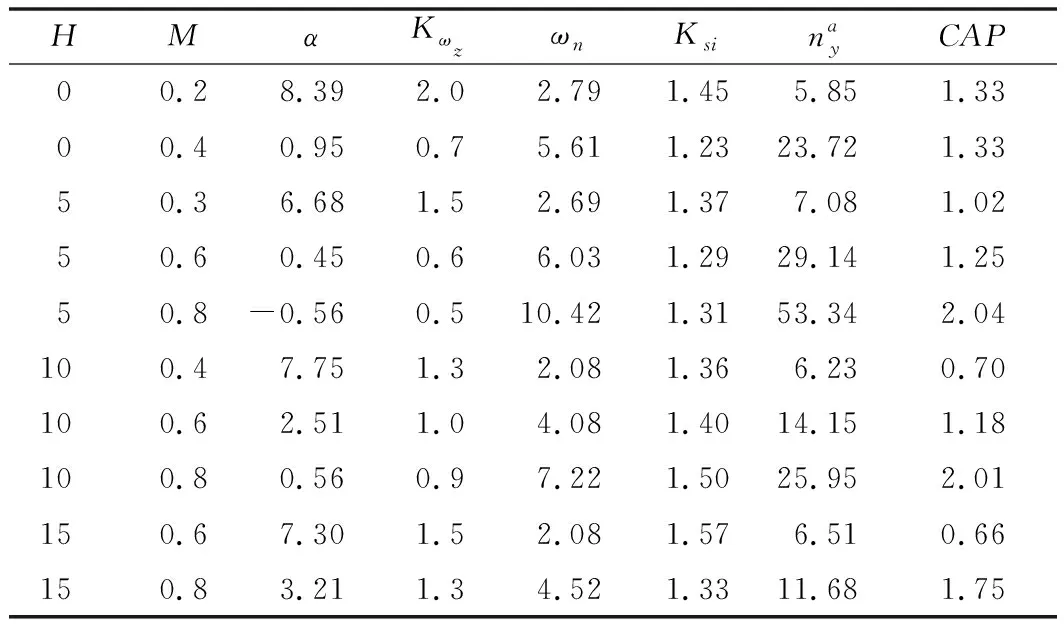
表6 加入Kωz反馈后的短周期模态特性

从图5纵向短周期频率特性计算结果可以看出，纵向增稳控制律在增加俯仰角速率反馈后，飞机的短周期阻尼特性、频率特性和操纵期望参数等满足GJB 185-1986标准1要求，因此可以不再增加迎角等反馈。

4.2 内回路横航向控制律设计

根据2.2节飞机本体横航向模态特性分析，为改善飞机飞行品质，加入Kβ反馈，增强航向静稳定性；加入Kωy反馈，改善荷兰滚模态特性；加入Kωx反馈，改善滚转模态特性。横航向增稳系统结构如图6所示。加入横航向反馈后的舵面偏转规律表达式为

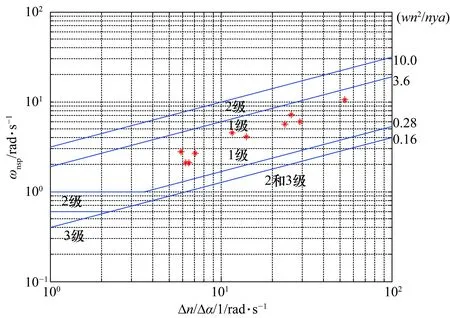
图5 纵向反馈控制后的短周期频率特性

δoe=δoec+Kωx×ωxt

(7)

δsdr=Kωy×ωyt+Kβ×β

(8)

式中，δiec为横向外回路控制律信号输出;Kωx为倾斜角速率反馈增益;Kωy为航向角速率反馈增益;Kβ为侧滑角反馈增益。

图6 横航向增稳系统结构

横航向加入内回路反馈后再次计算横航向模态特性，近似计算中的使用的当量大导数为

(9)

(10)

荷兰滚频率设计目标值为2 rad/s，阻尼比设计目标值为0.7，滚转时间常数设计目标值为0.1 s。根据设计目标值调整横航向反馈增益Kβ、Kωx、Kωy，加反馈增稳后的荷兰滚阻尼比、频率和滚转时间常数特性如表7所示，荷兰滚模态特性计算结果如图7所示。

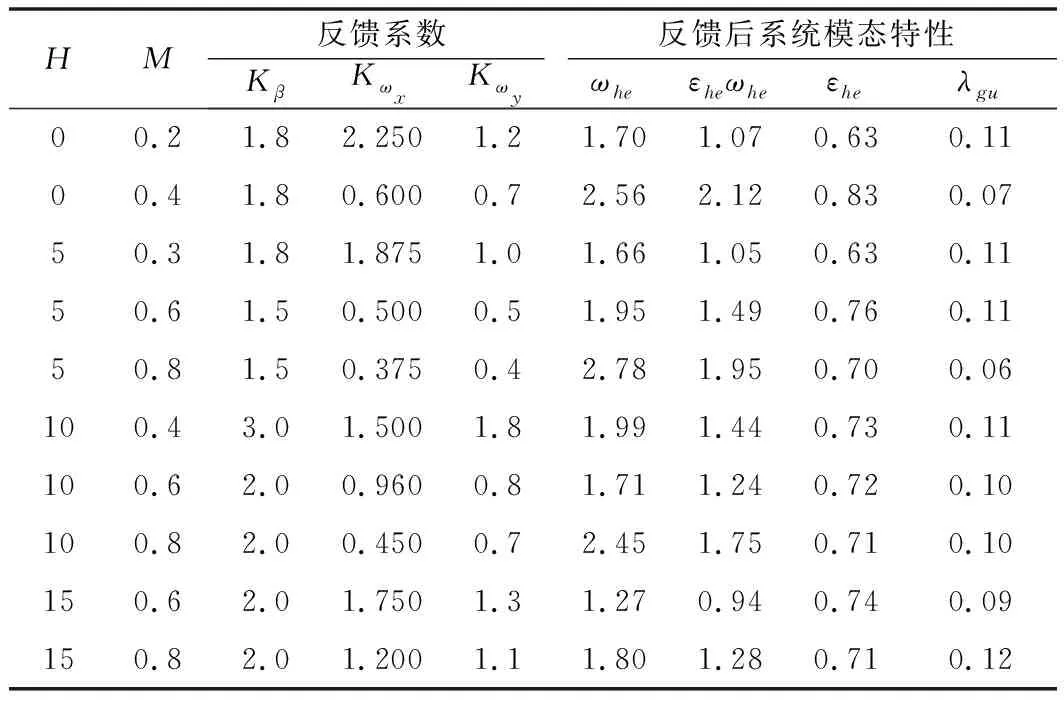
表7 本体横航向模态特性、横航向反馈和反馈后模态特性

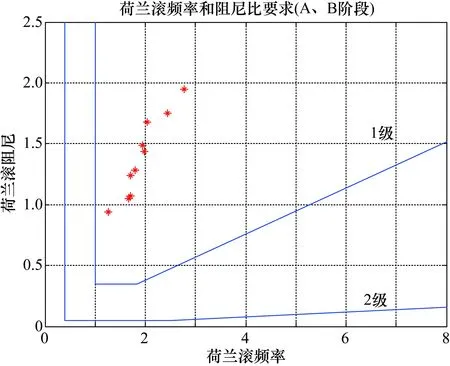
图7 横航向加入反馈后的荷兰滚模态特性

从计算结果可以看出，经Kβ、Kωx、Kωy反馈补偿后的横航向模态特性满足GJB 185-1986中荷兰滚模态特性标准1要求。

5 外回路控制律设计

在线性小扰动方程内回路增稳控制的基础上增加外回路控制器，设计PI控制器，进行参数调参。本文主要使用比例环节P和积分环节I通过差量驱动控制。

PI控制器调参规律需满足GJB 2191-1994中关于自动驾驶保持精度要求，相对于基准值的静态精度应满足下列指标：

① 航向角保持精度：±0.5°；

② 倾斜角保持精度：±1°；

③ 俯仰角保持精度：±0.5°；

④ 气压高度保持精度(平飞状态)：±9 m(0～9000 m)；±0.1%H(9000 m～升限)。

5.1 俯仰角控制律设计

俯仰角控制律表达式为

(11)

式中，Theta_C为目标俯仰角；Theta为飞机当前俯仰角；Ktheta_p为俯仰角控制的比例增益；Ktheta_i为俯仰角控制的积分增益。

俯仰角控制律结构如图8所示，输出δie为内侧升降副翼控制指令，舵面限幅值为最大可偏转角度为±20°。

图8 俯仰角控制律

5.2 高度控制律设计

高度控制律表达式为

(12)

式中，H_C为目标高度；H为飞机当前高度；Kh_p为高度控制比例增益；Kh_i为高度控制积分增益；Theta_JT为接通时刻俯仰角。

高度控制律结构如图9所示，输出俯仰角控制指令Theta_C给俯仰角控制律，俯仰角限幅值为-15°～20°。

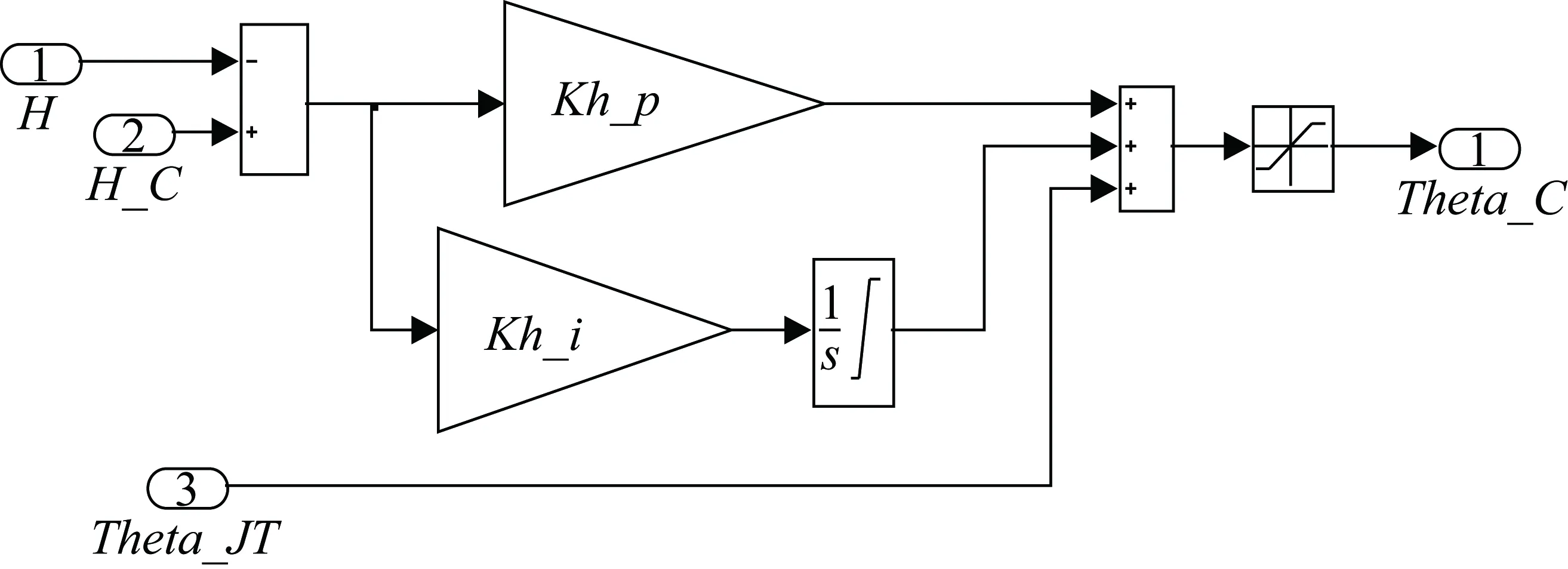
图9 高度控制律

5.3 倾斜角控制律设计

倾斜角控制律表达式为

(13)

式中，Gama_C为目标倾斜角；Gama为飞机当前倾斜角；Kgama_p为倾斜角控制的比例增益；Kgama_i为倾斜角控制的积分增益。

倾斜角控制律结构如图10所示，输出δoe为外侧升降副翼控制指令，舵面限幅值为最大可偏转角度±20°。

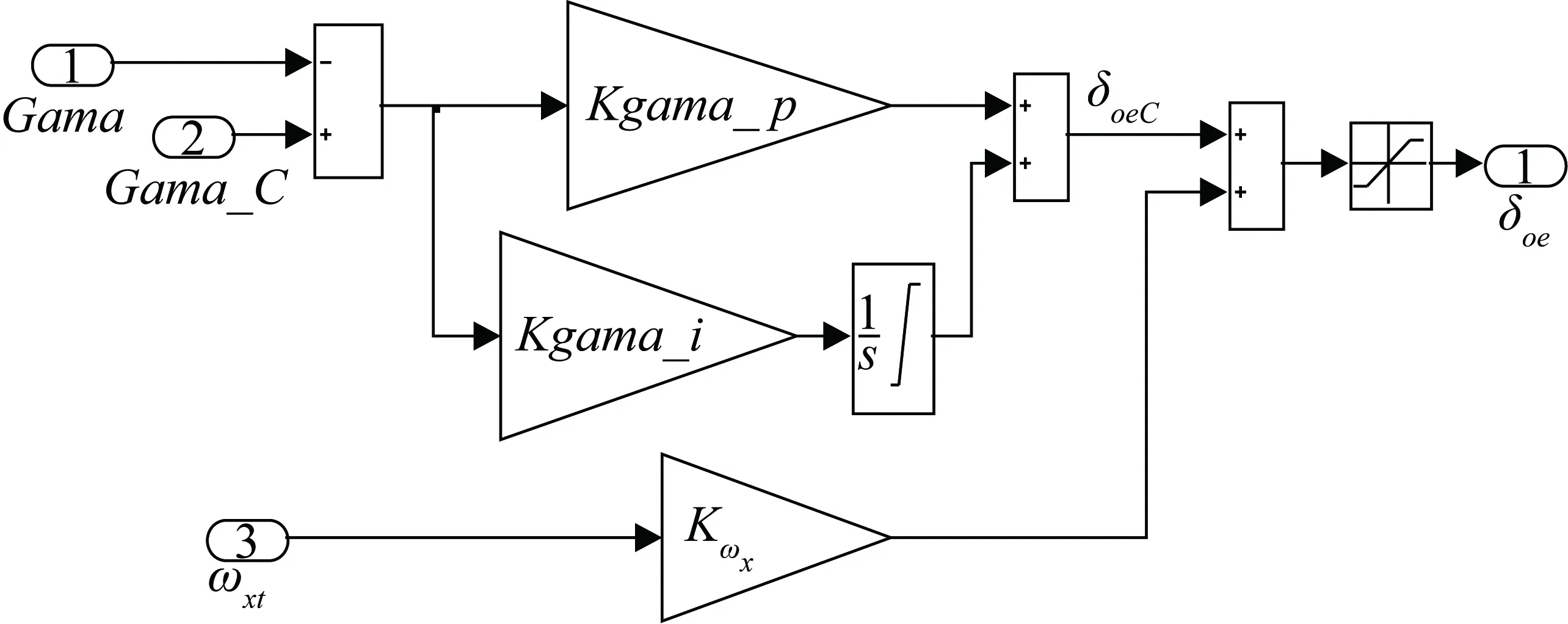
图10 倾斜角控制律

5.4 航向角控制律设计

航向控制律表达式为

Gama_C=(Psi_C-Psi)×Kpsi-CET×Kcet

(14)

式中，Psi_C为目标航向角；Psi为飞机当前航向；Kpsi为航向角控制增益；CET为飞机与目标航线的距离偏差；Kcet为侧向距离控制增益。

航向角控制律结构如图11所示，输出倾斜角控制指令Gama_C给倾斜角控制律，倾斜角限幅值为±40°。

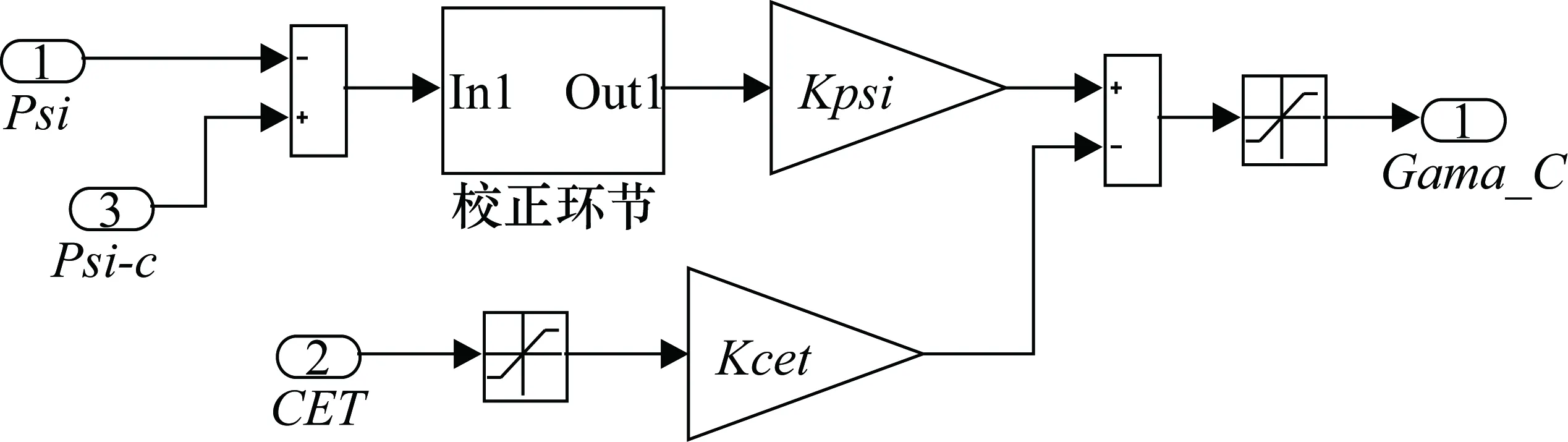
图11 航向角控制律

校正环节算法如下：

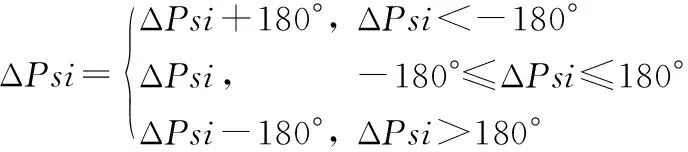
(15)

5.5 速度控制律设计

速度控制律表达式为

(16)

式中，P为发动机推力;V_C为目标速度；V为飞机当前速度；Kv_p为速度控制比例增益；Kv_i为速度控制比例增益。

速度控制律结构如图12所示，输出为飞机发动机推力，推力增大限幅值为500 kg×f。

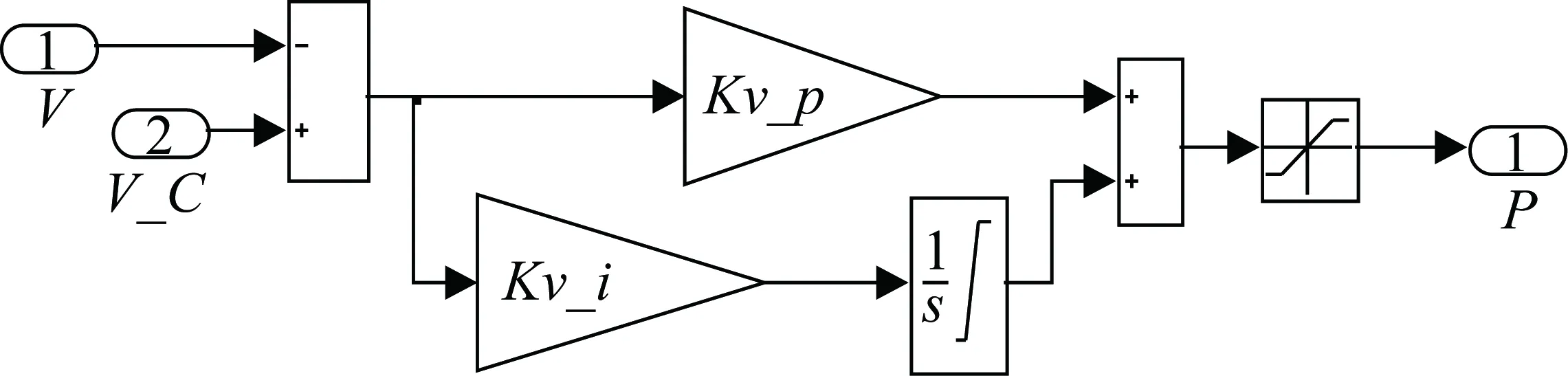
图12 速度控制律

6 稳定裕度分析

分别建立上述各子模态的线性小扰动模型，以高度保持控制模态为例，建立的线性稳定裕度计算模型如图13所示。将输入In和输出Out之间的模型进行二阶系统等效，绘制系统伯德图并计算稳定裕度。由于篇幅限制，此处省略其他子模态建模及稳定裕度计算结果。

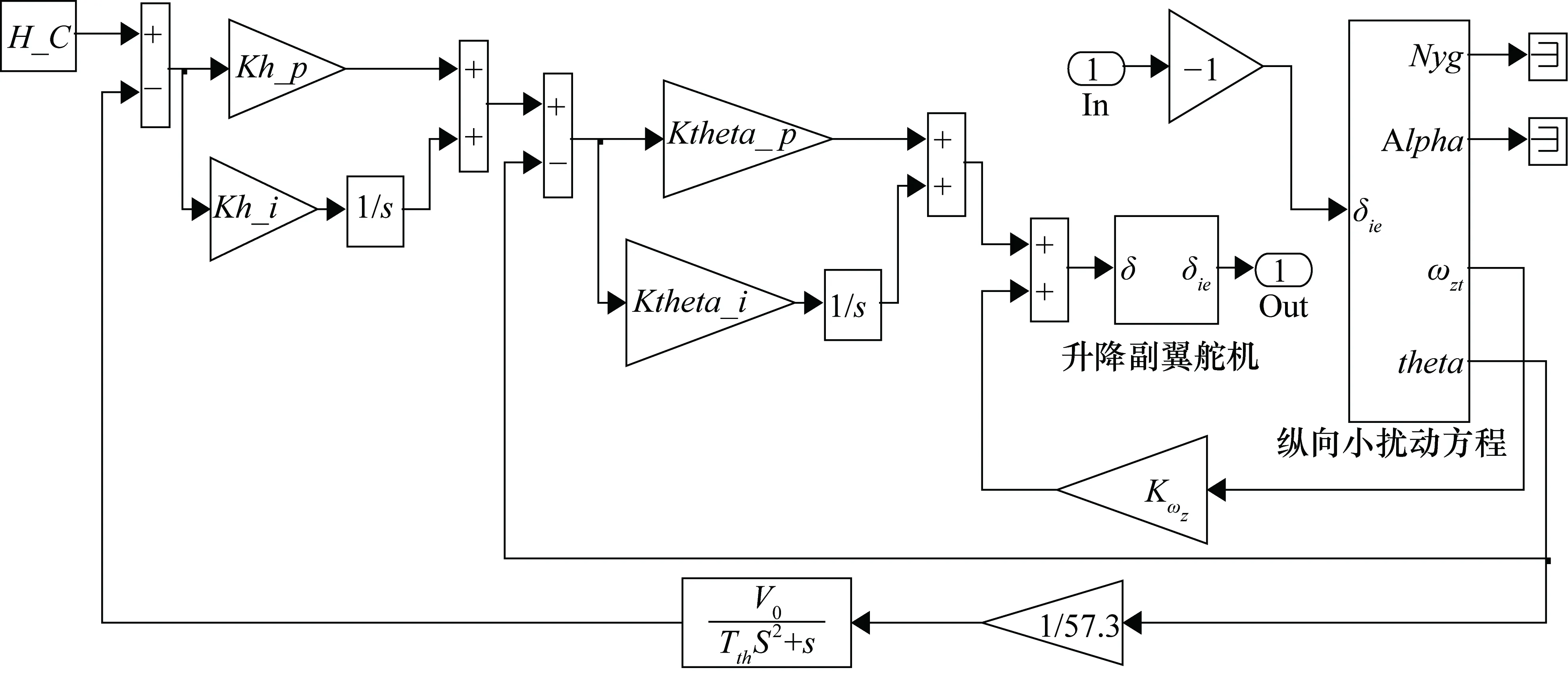
图13 高度保持模态稳定裕度计算线性化模型框图

所有子模态的稳定裕度计算结果满足GJB 2191-1994中相位储备大于45°、幅值储备大于6 dB的要求。

7 六自由度仿真分析

根据第1节中飞翼布局无人机力和力矩的模型，建立六自由度动力学仿真模型，飞机方程采用的运动方程组为“机体—机体”体系，即飞机质心的动力学方程和转动的动力学方程都在机体坐标系中建立。飞机方程模型的方程组如式(17)～式(28)所示。

(17)

(18)

(19)

(20)

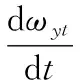
(21)

(22)

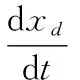
(23)

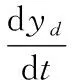
(24)

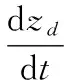
(25)

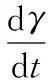
(26)

(27)

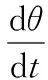
(28)

记录内回路增稳反馈参数和外回路控制器参数随高度和马赫数的变化，内、外回路控制律结构如图14所示，其中俯仰角控制、高度控制、倾斜角控制和航向角控制模块按照第5节内容进行建模。

以H=5 km，M=0.4为配平状态，在仿真时间5 s时输入俯仰角控制指令Theta_C=10°给外回路控制律，在仿真时间15～16 s时加入俯仰力矩系数拉偏+50%，仿真结果如图15所示。

在仿真时间8 s时俯仰角达到指令要求，与目标值偏差小于0.5°，符合GJB 2191-1994中对俯仰角控制精度的要求，俯仰角变化过程中最大法向过载约2g。15 s加入气动参数拉偏后，飞机有较为明显的抬头趋势，控制律能够驱动舵面偏转使俯仰角快速回到控制目标值，俯仰角控制回路具有较好的系统稳定性和鲁棒性。

仿真时间5 s时输入高度控制指令H_C=5100 m给外回路控制律，仿真时间25～26 s时加入俯仰力矩系数拉偏+200%，仿真结果如图16所示。

在仿真时间17 s时高度达到指令要求，与目标值偏差小于9 m，符合GJB 2191-1994中对高度控制精度的要求，过程中最大俯仰角限制为10°，最大法向过载不大于2g。加入拉偏后，高度能够较为快速地回到控制目标值，高度控制回路具有较好的系统稳定性和鲁棒性。

仿真时间5 s时输入倾斜角控制指令Gama_C=30°给外回路控制律，在仿真时间15～16 s时加入滚转力矩系数拉偏+200%，仿真结果如图17所示。

在仿真时间10 s时，倾斜角达到指令要求与目标值偏差小于1°，符合GJB 2191-1994中对倾斜角控制精度的要求。加入拉偏后，倾斜角能够回到目标值，倾斜角控制回路具有较好的系统稳定性和鲁棒性。

仿真时间5 s时输入航向角控制指令Psi=10°给外回路控制律，在仿真时间30～31 s时加入偏航力矩系数拉偏+200%，仿真结果如图18所示。

在仿真时间25 s时，航向角达到指令要求与目标值偏差小于0.5°，符合GJB 2191-1994中对航向角控制精度的要求，控制时间偏长。加入拉偏后，航向角几乎没有响应，航向角控制回路具有较好的系统稳定性和鲁棒性。

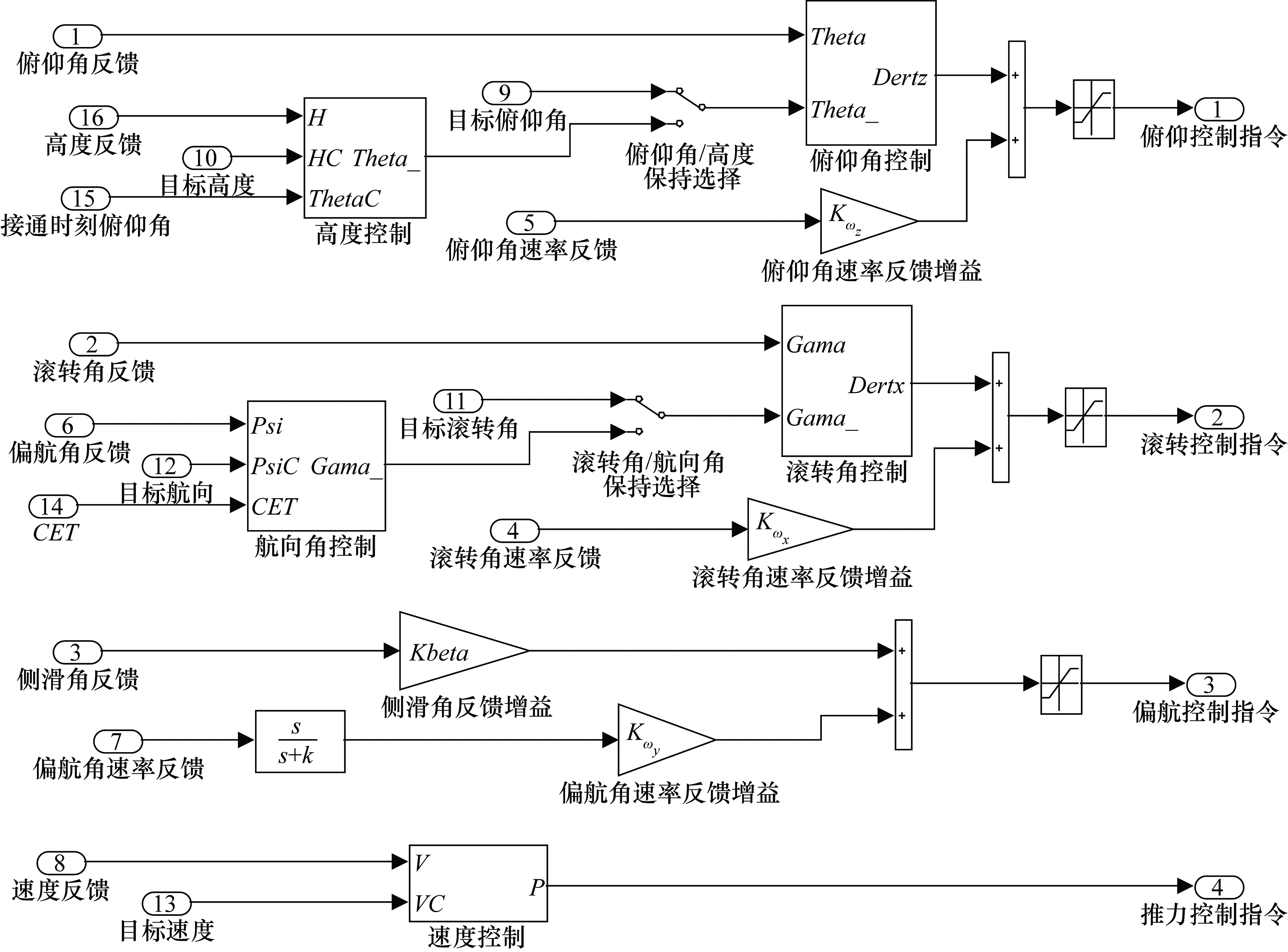
图14 六自由度仿真模型中内、外回路控制律结构示意图

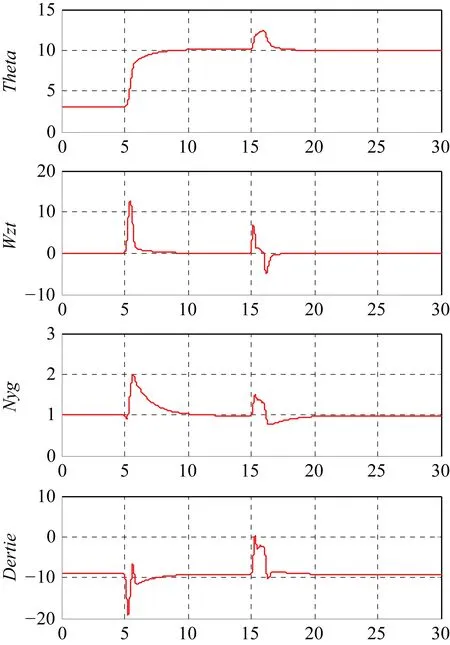
图15 0504状态点俯仰角Theta_C=10°仿真结果

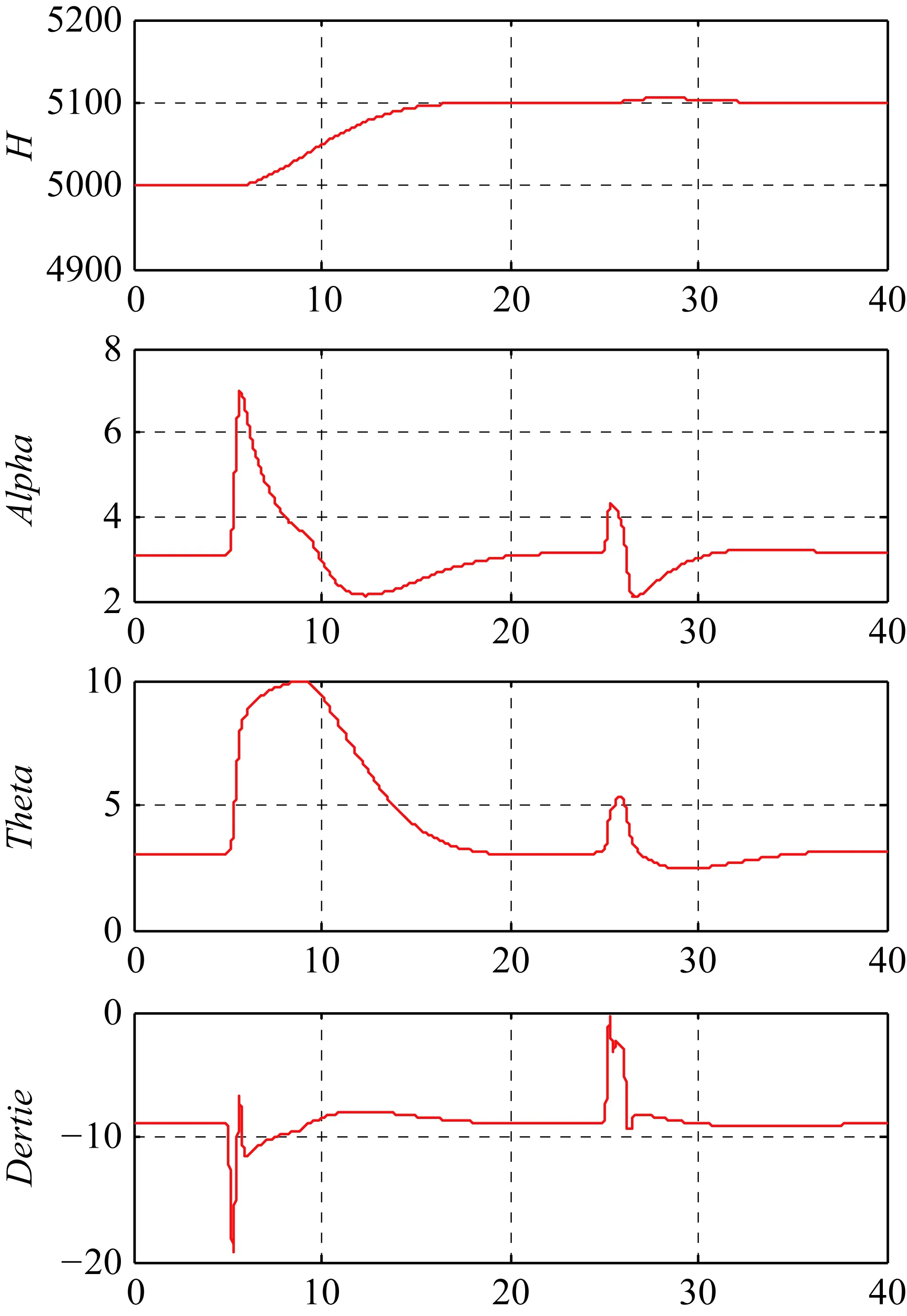
图16 0504状态点高度H_C=5100m仿真结果

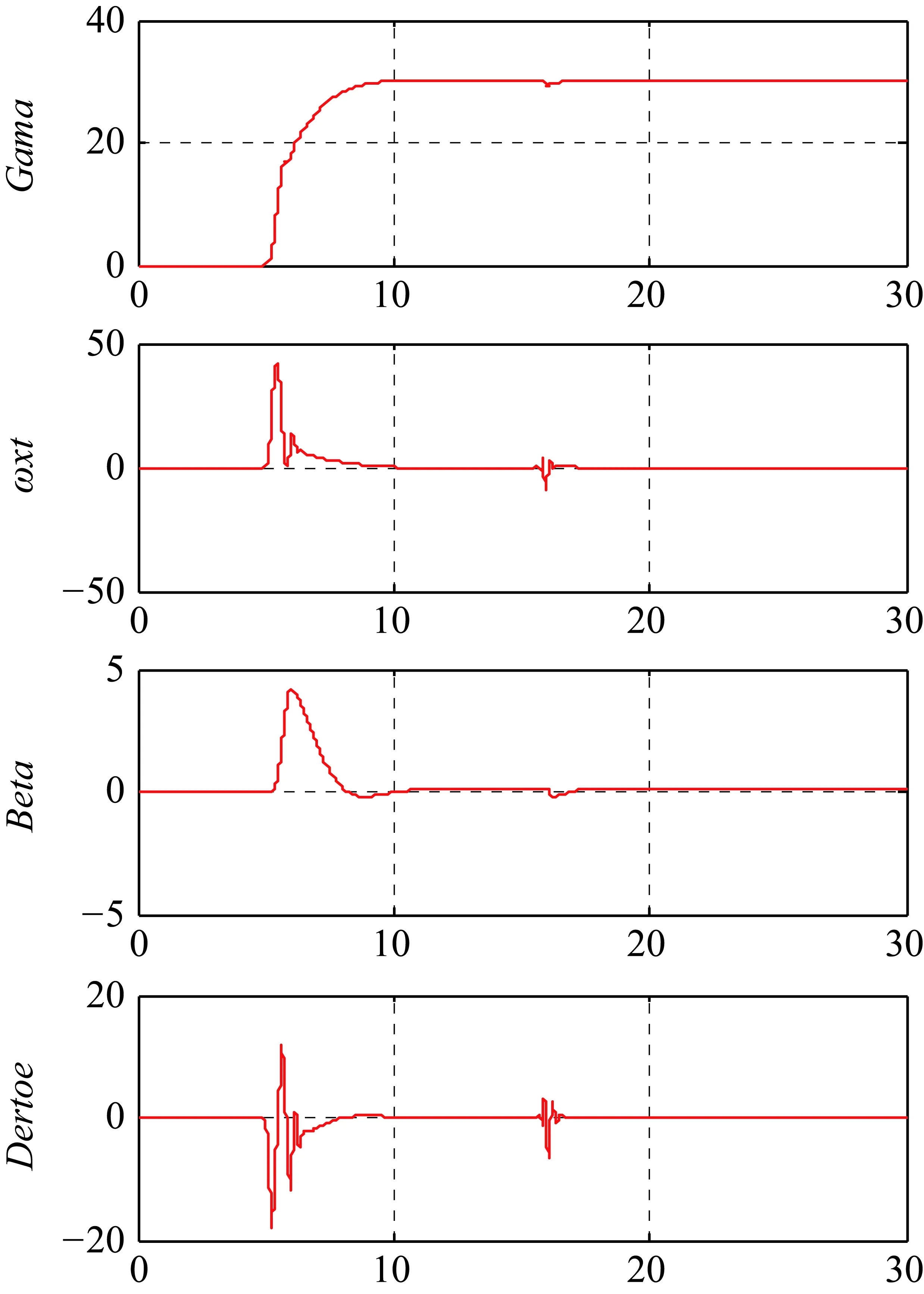
图17 0504状态点倾斜角Gama_C=30°仿真结果

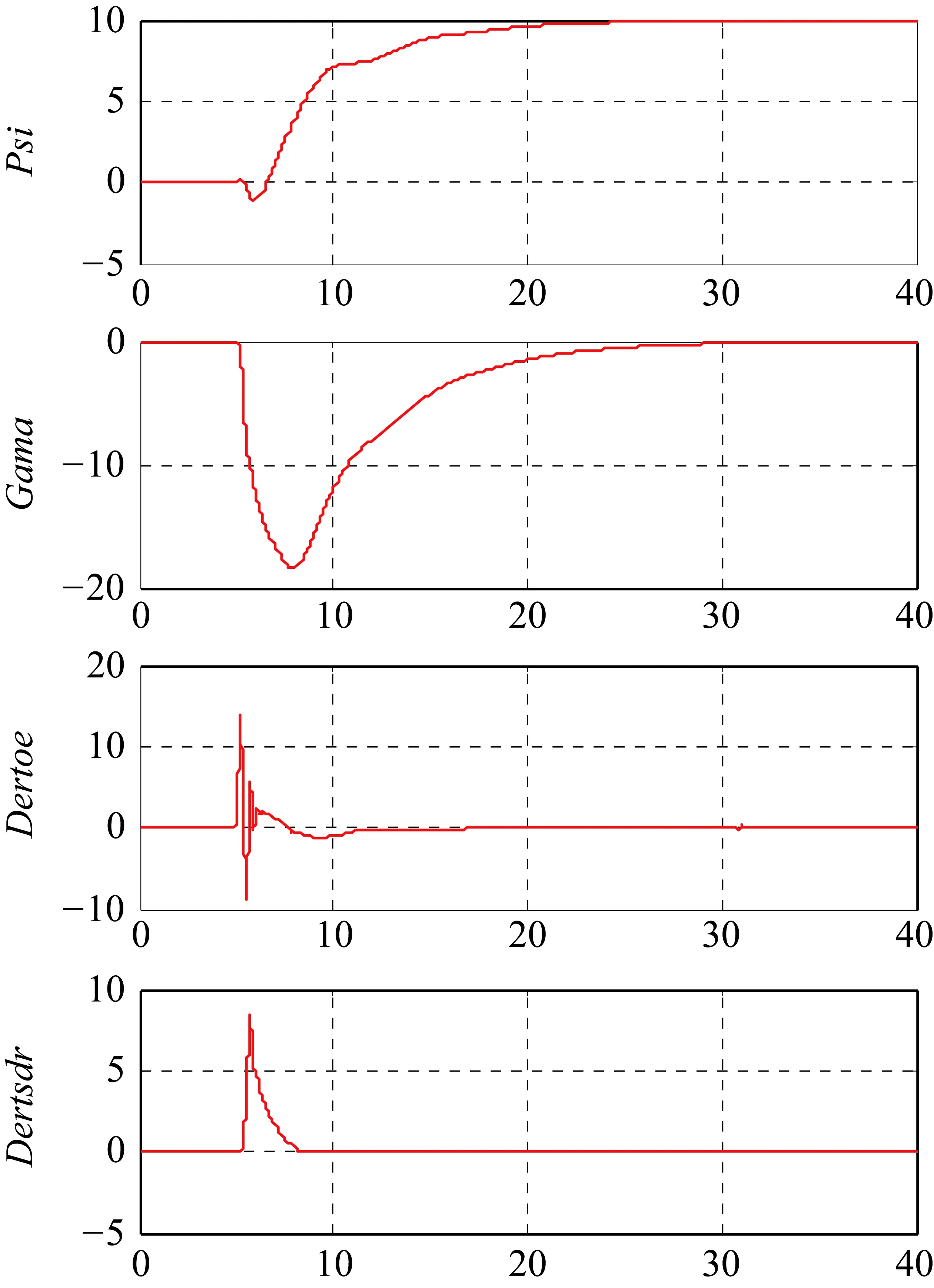
图18 0504状态点航向角Psi=10°仿真结果

8 结束语

以某飞翼布局无人机为对象，设计的内回路增稳控制律能够使飞机三轴模态特性满足GJB 185-1986飞行品质要求；设计的外回路控制律能够实现飞机姿态控制，且系统稳定裕度满足GJB 2191-1994要求。

建立六自由度非线性仿真模型，仿真验证结果表明目标控制稳态精度满足GJB 2191-1994要求，且鲁棒性良好。

内、外回路控制律设计方法可行，控制精度高，具有良好的鲁棒性，后续可结合导航控制律实现三维导航控制。