基于PI+自适应内模重复控制的并网逆变器系统研究
边庆超,胡 铭,杨沛豪
(1.青岛黄海学院大数据学院,青岛 266427;2.安徽工业大学电气与信息工程学院,马鞍山 243032;3.西安热工研究院有限公司,西安 710054)
为了提高太阳能、风力等分布式新能源发电并网的电能质量,降低并网电流的谐波畸变率THD(total harmonic distortion),国内外专家对并网逆变器控制策略进行了大量研究。
为了提高风力发电的实际应用能力,文献[1]提出一种改进型比例-谐振[2-3]控制方法,可以在两相静止坐标系下消除并网电流中的谐波,同时在电流环中引入网侧电压前馈控制,用以提高系统的动态性能;文献[4]提出一种准比例谐振控制+重复控制的组合控制方案,通过采用参考电流前馈来消除系统延时问题,采用比例控制提高了整体的动态性能,当负载突变时,依然能够保证良好的控制性能,但谐振控制只能在特定次谐波处产生谐振,当需要抑制网侧电流中的多次谐波时,需要并联多个谐振控制器,增加了系统的设计难度;针对LCL型光伏发电并网逆变器在低功率运行状态下[5-6]控制性能较差的问题,文献[7]提出一种用逆变器瞬时输出功率来控制IGBT开关频率的控制策略,具体是在网侧电压矢量控制[8-9]的基础上引入频率控制环[10],用以确定当前瞬时功率下的最佳开关频率,但该算法需要实时在线计算,计算量很大,导致系统响应时间变长;文献[11]以T型三电平逆变器[12]作为研究对象,同时针对粒子群优化算法PSO(particle swarm optimization)的特点[13-15],提出一种自适应 PSO[16]控制算法,通过改进型PSO算法,建立非线性方程组,求解非线性方程组得到几组解,并分析了不同解对谐波的抑制作用,最后选出最优控制解,PSO算法虽然计算速度快,但容易出现局部最优的问题。
本文在参考以上文献的基础上,提出一种PI+自适应内模重复控制方案。用一个实时在线计算的数字滤波器代替传统重复控制中的低通滤波器,当电网频率发生波动时,该数字滤波器可以快速调节参数,保证重复控制的谐振频率与电网频率一致;同时,考虑到单一重复控制动态性能不佳的问题,在自适应内模重复控制的基础上结合PI控制,并对前相通道和参考指令信号进行改进,有效抑制了组合控制系统由于时序不同而引起的控制耦合;最后,通过仿真和实验,验证了该方案既能提高系统的抗电网频率干扰能力,又能提高系统的动态响应速度。
1 LCL并网逆变器数学模型
并网逆变器常见的拓扑结构为L型和LCL型,L型拓扑结构虽然结构简单,但电感参数值较大,且高频段信号抑制能力较弱,本文将LCL型逆变器拓扑结构作为研究对象,如图1所示。
图1中:u为逆变器输出电压;ug为并网电压;if为逆变器输出电流;ig为并网电流;Udc为直流母线电压;Cdc为直流侧并联大电容;Lf、Lg、Cf、Rf和 Rg构成了LCL型并网逆变器的拓扑结构,ABC三相坐标系下其数学模型为
式中:ifi为逆变器第i相输出电流;uCi为逆变器第i相滤波电容对地电压;ui为逆变器第i相输出电压;igi为逆变器第i相并网电流。
对式(1)进行Clarke变换,可以得到αβ两相静止坐标系下的数学模型为
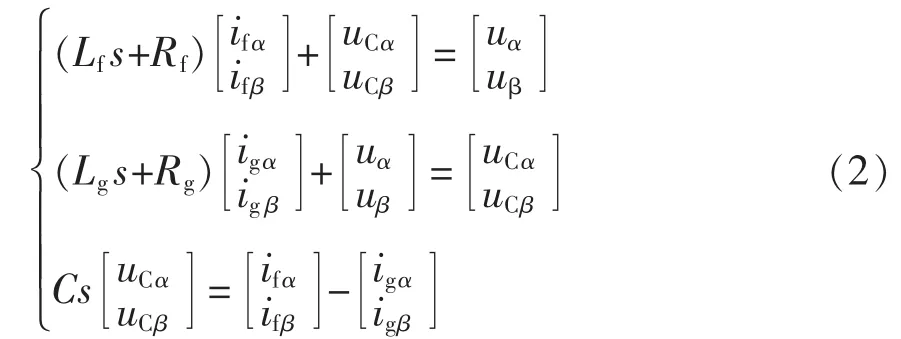
由式(2)可知,在αβ两相静止坐标系下,各变量之间无耦合项,不涉及2个轴之间的解耦问题,方便控制系统的设计,因此本文将αβ两相静止坐标系下的LCL型并网逆变器作为研究对象。
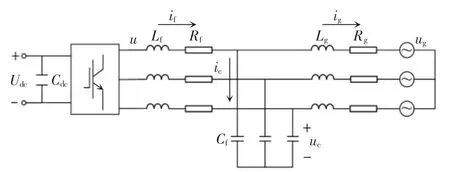
图1 LCL型三相并网逆变器拓扑结构Fig.1 Topology of LCL three-phase grid-connected inverter
当网侧电压或频率出现波动时,传统PI控制无法准确跟踪参考指令电流,对网侧电压或频率波动造成的谐波干扰无法有效抑制,因此,需要采用能够抑制周期性扰动且准确跟踪参考指令电流的重复控制。
2 自适应内模重复控制
自适应内模重复控制原理如图2所示。图中:Iref(z)为参考指令电流;Io(z)为输出电流;E(z)为电流误差;N=f1/f2,其中f1为系统采样频率,f2为电网频率,N的小数部分为d,N的整数部分为Ni;当电网频率发生波动时,比值N通常不是一个整数,会造成重复控制的谐振频率偏离电网实际频率,从而降低控制性能,因此,本文提出一种自适应内模重复控制。
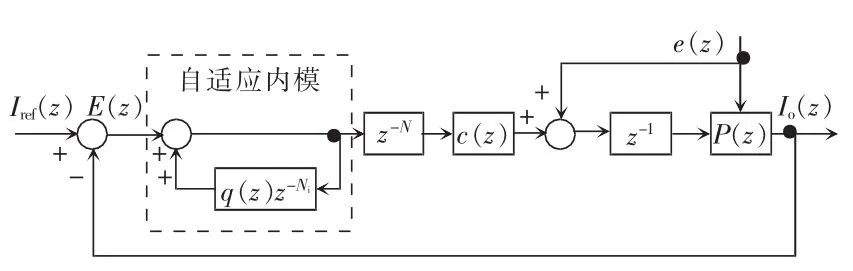
图2 自适应内模重复控制原理Fig.2 Principle of repetitive control of adaptive internal mode
自适应内模重复控制由延迟环节z-N、补偿环节c(z)和自适应内模 1/[1-q(z)z-Ni]三部分组成。①延迟环节z-N的主要目的是让补偿环节c(z)中zk能够实现;②通常令补偿环节 c(z)=Krzks(z),其中Kr为重复控制增益系数,zk为相位补偿环节,zk是一个整数,相位补偿环节zk的主要作用是对LCL型逆变器传递函数P(z)和滤波环节s(z)引起的相位滞后进行补偿,滤波环节 s(z)的作用是使 z-1P(z)·s(z)在低频段保持恒定增益,在高频段迅速衰减;③自适应内模在传统重复控制系统中,Q(z)是一个低通滤波器或者是小于1的常数,当电网频率发生波动时,无论Q(z)选择哪个,都会使重复控制内模偏离重复控制理想内模1/(1-z-N)。针对以上问题,采用一种自适应数字滤波器取代传统Q(z),自适应数字滤波器的传递函数可以写成

将式(3)在时域下展开可得
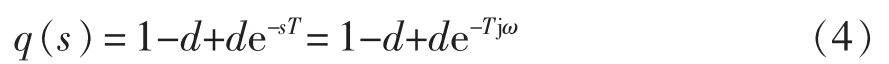
式中,T为系统采样周期。延迟环节z-d在时域下的形式可表示为

对式(4)和式(5)进行展开,可以分别得到
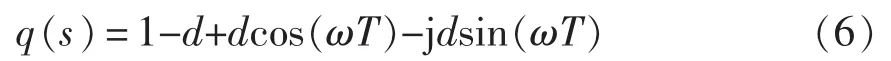
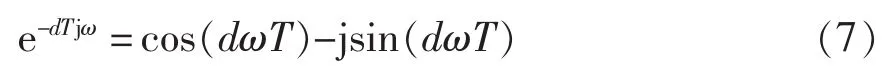
设式(6)和式(7)相等,可以得到
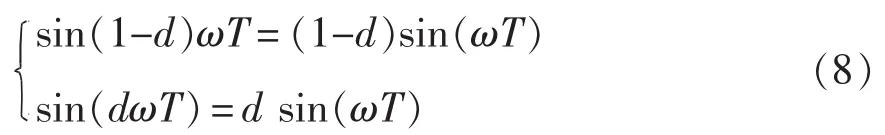
由于电网基波频率和3次、5次、7次等主要低次谐波频率相对于采样频率f1来说比较小,故

将式(9)代入式(8),可以证明式(8)成立。q(z)的系数由小数d构成,q(z)的作用是趋近延迟环节z-d,当 d(z)和 z-Ni串联后,能够使自适应内模趋近于理想内模1/(1-z-N)。当电网频率出现波动时,由PLL实时在线计算系统采样频率与电网频率的比值N、q(z)的系数d和延迟环节 z-Ni的 Ni,使自适应内模重复控制的谐振频率与电网频率同步。
传统重复控制内模、重复控制自适应内模和理想重复控制内模的幅频、相频特性曲线如图3所示。
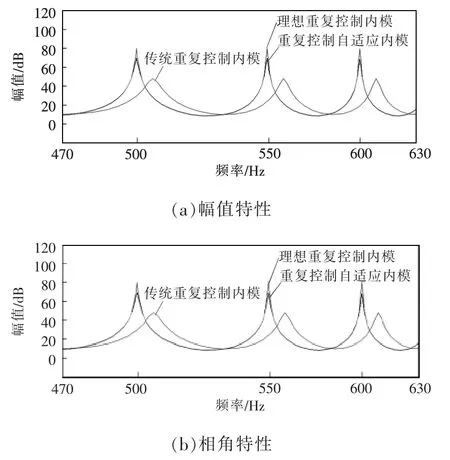
图3 3种重复控制内模Bode图Fig.3 Bode diagram of three kinds of repetitive control of internal mode
图3中,设系统采样频率f1=10 kHz,电网频率f2=50.3 Hz,此时 N=f1/f2=198.8,则 Ni=198,d=0.8。从图中可以看出,传统重复控制内模在谐振频率处明显偏离理想重复控制内模,控制性能较差;而重复控制自适应内模能够最大程度逼近理想重复控制内模(即Q=1,但理想重复控制内模在实际中不能实现),具有良好的抗电网频率干扰能力和谐波抑制能力。
自适应内模重复控制虽然具有良好的抗电网频率干扰能力和谐波抑制能力,但由于单一重复控制动态响应速度并不快,且Ni的实时在线计算,更加降低了其动态性能,因此,将PI控制结合到自适应内模重复控制中,既可以保证良好的抗电网频率干扰能力,又可以提高系统的动态性能,基于PI+自适应内模重复控制原理如图4所示。

图4 PI+自适应内模重复控制原理Fig.4 Principle based on PI and repetitive control of adaptive internal mode
由图 4 可得从 Iref(z)到 E(z)的脉冲传递函数为

由式(10)可以得到G(z)的单位阶跃响应Bode图,如图5所示。
由图5可以看出,当参考指令电流阶跃突变时,在一个周期内,电流误差快速衰减并趋于稳定,但一个周期后,电流误差又会出现并衰减,这种周期性出现的电流误差会导致并网电流出现畸变。
为得到周期性电流误差,分别给出从 Io(z)、uPI(z)和 uRC(z)到参考电流 Iref(z)的脉冲传递函数,即
图 6 为 G1(z)、G2(z)和 G3(z)的阶跃响应曲线。从图 6(a)和(b)可以看出,参考指令电流 Iref(z)的突变会引起误差信号e(z)突变,在第1个周期(即0.02 s)时间内,由于重复控制存在一个周期延迟,输出uRC(z)无变化,在一个周期时间后,重复控制才输出相应的阶跃响应信号,而PI控制则立即响应。从图6(c)可以看出,在起始阶段,系统虽然能够很快稳定,但由于重复控制存在一个周期的延迟,使得输出电流在一个周期后发生突变,且该突变存在周期性。
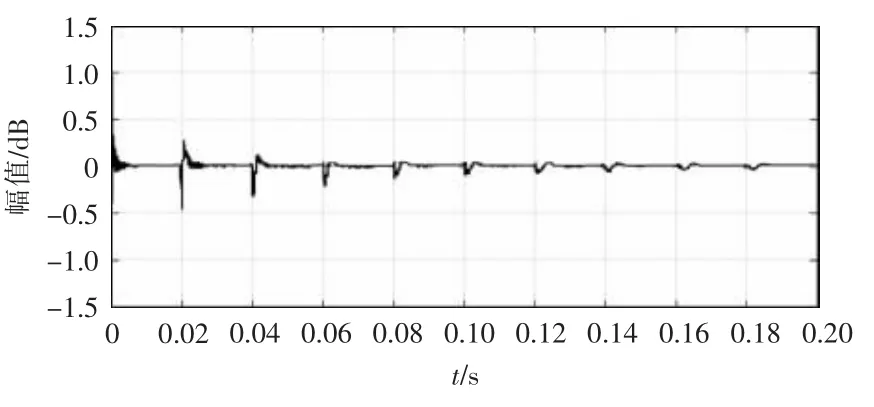
图5 G(z)单位阶跃响应Bode图Fig.5 Bode diagram of G(z) unit step response
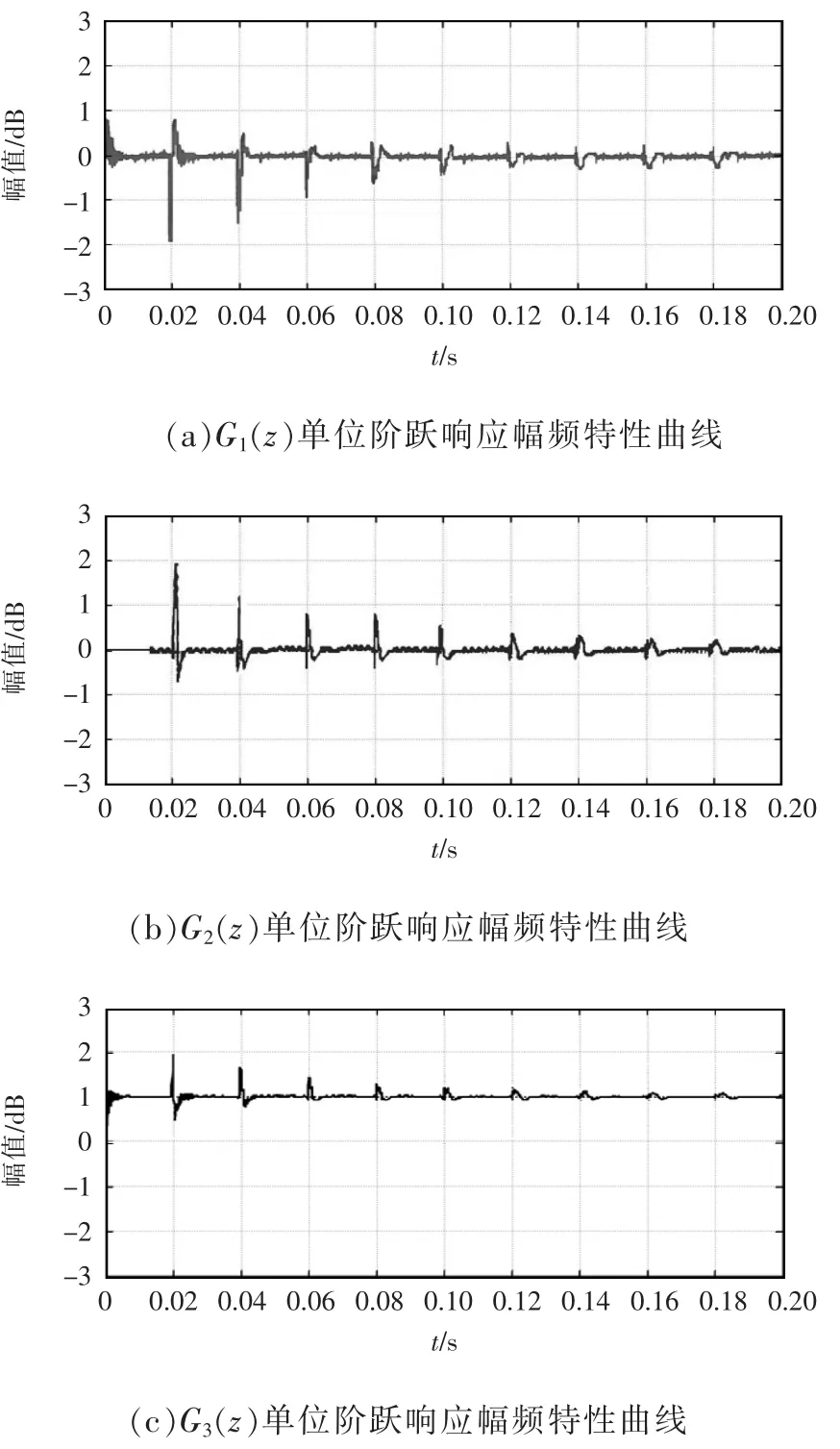
图6 3种传递函数的单位阶跃响应Bode图Fig.6 Bode diagram of unit step response for three transfer functions
由上述分析可以看出,PI+自适应内模重复控制的这种周期性误差现象是由2个控制器之间的耦合引起的,而造成2个系统耦合的原因是2个控制器的响应时间不同,导致输出电流在每个周期都会产生瞬时突变。针对这一问题,对PI+自适应内模重复控制的前向通道和参考指令电流进行改进,改进后的控制系统原理如图7所示,基于αβ两相静止坐标系下的电流环控制策略相同,因此以α轴电流环控制进行说明。

图7 改进后的PI+自适应内模重复控制原理Fig.7 Improved principle based on PI and repetitive control of adaptive internal mode
为了提高PI+自适应内模重复控制的动态响应速度,消除2个控制器结合在一起使用时的耦合影响,需对PI+自适应内模重复控制的前向通道做如下修改:①前向通道中的PI控制改为P控制,且满足KPKr=1;②前向通道直接利用参考指令电流,而不是电流误差。
通过串联一个k+k1相位补偿环节,实现对参考信号的k+k1超前,其中:k与zk中的k相同,k1为在k拍的基础上再超前θ1,θ1可表示为

对前向通道改进的理论基础是0相位跟踪原理,即使输入到输出的传递函数为1,最大限度地保证系统的动态性能。当参考指令电流发生突变时,在PI+自适应内模重复控制的一个延迟周期内,系统近似为一个开环系统,则从参考指令电流到实际电流的脉冲传递函数可表示为
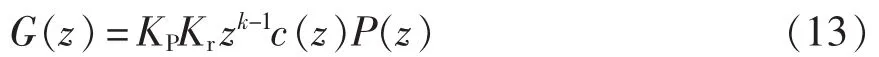
当自适应内模重复控制的幅值和相位选择合适时,即 zk-1c(z)P(z)=1,将 KPKr=1 代入式(13),可得

由式(13)和式(14)可以看出,在参考指令电流发生突变的一个周期内,系统为一个0相位跟踪系统,保证了其较好的动态性能。
为消除控制系统间的控制耦合问题,在PI+自适应内模重复控制的参考指令电流上加入延迟环节,延迟环节由k+k2相位补偿模块和滞后模块z-d串联而成,当参考指令电流发生突变时,抑制2个控制器之间控制耦合的延迟环节原理如图8所示。
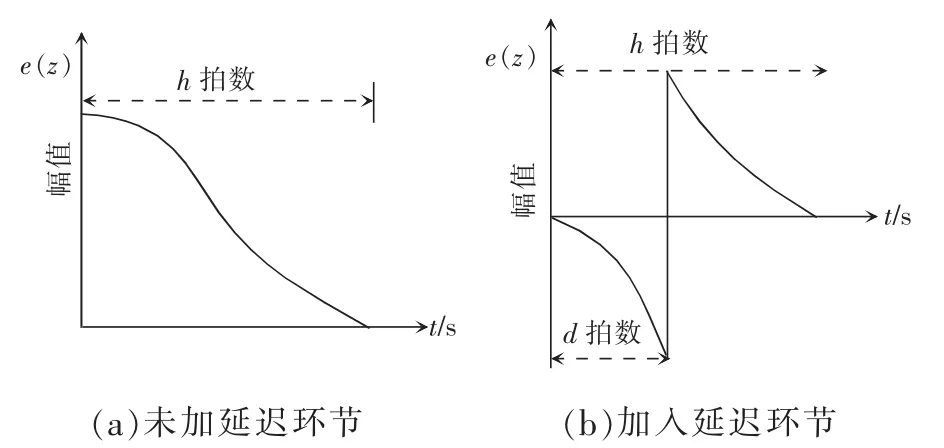
图8 基于延迟环节的控制耦合抑制原理Fig.8 Principle of control coupling suppression based on delay module
由图8可以看出,未加入延迟环节时,当参考指令电流发生突变时,误差信号也突变,参考指令电流的突变峰值等于误差信号的突变峰值,经过h拍后,系统达到稳定状态;加入延迟环节时,延迟环节对参考指令信号具有d拍延迟,即在d拍内,由于PI+自适应内模重复控制的参考指令电流不发生变化,此时误差为负值,在d拍后,误差才发生突变。因此,在PI+自适应内模重复控制的参考指令电流加入延迟环节时,误差峰-峰值降低为原来的1/2,而误差峰-峰值的降低使下一个周期的输出干扰控制量降低,从而抑制耦合。
3 仿真分析
为验证所提方法的有效性,在Matlab/Simulink中搭建了基于PI+自适应内模重复控制的LCL型并网逆变器模型,逆变器参数为:额定功率为6 kW,直流母线电压为420 V,开关频率为5 kHz,系统采样频率为10 kHz,逆变器侧电感为1.5 mH,网侧电感为1 mH,直流母线侧电容为4 700 μF,滤波电容为10 μF,逆变器侧电阻为0.5 Ω,网侧电阻为0.05 Ω。Kr=0.85,KP=1/0.85,二阶低通滤波器,补偿环节 c(z)中的超前补偿。
3.1 抗电网频率扰动性能的仿真验证
为了验证PI+自适应内模重复控制的抗电网频率扰动能力,假设电网频率变为50.3 Hz,满载运行时,传统重复控制和PI+自适应内模重复控制下的并网逆变器A相输出电流及输出电流跟踪误差波形如图9所示。
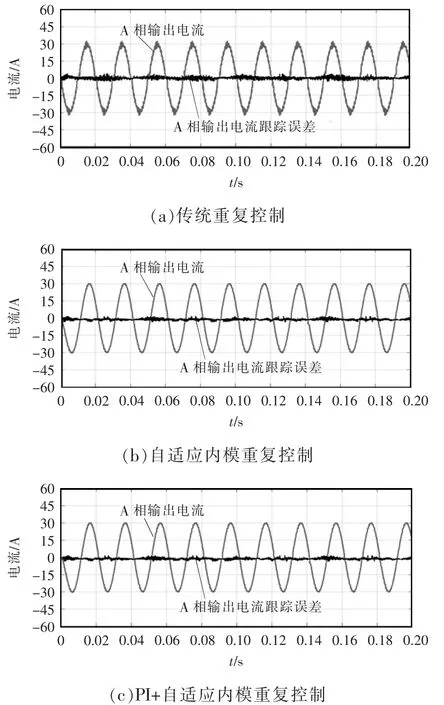
图9 A相输出电流及输出电流跟踪误差波形Fig.9 Waveforms of phase-A output current and output current tracking error
比较图9可以看出,当电网频率偏离50 Hz,为50.3 Hz时,传统重复控制下的A相输出电流正弦特性较差,峰值处纹波明显增大,A相输出电流与参考指令电流的误差峰-峰值为7.6 A,A相输出电流THD=3.68%;在自适应内模重复控制下,由于系统采样频率f1=10 kHz,电网频率f2=50.3 Hz,N=f1/f2=198.8,此时,Ni=198,d=0.8,自适应内模重复控制可以实时在线计算重复控制的内模参数,使其能够在电网频率出现波动时,准确跟踪参考指令电流,A相输出电流正弦稳定性得到提高,峰值处纹波降低,A相输出电流与参考指令电流的误差峰-峰值降为3.3 A;PI+自适应内模重复控制系统下的A相输出电流正弦特性、A相输出电流与参考指令电流的误差峰-峰值以及A相输出电流THD与自适应内模重复控制下的特征基本相同。A相输出电流的谐波畸变率如图10所示。
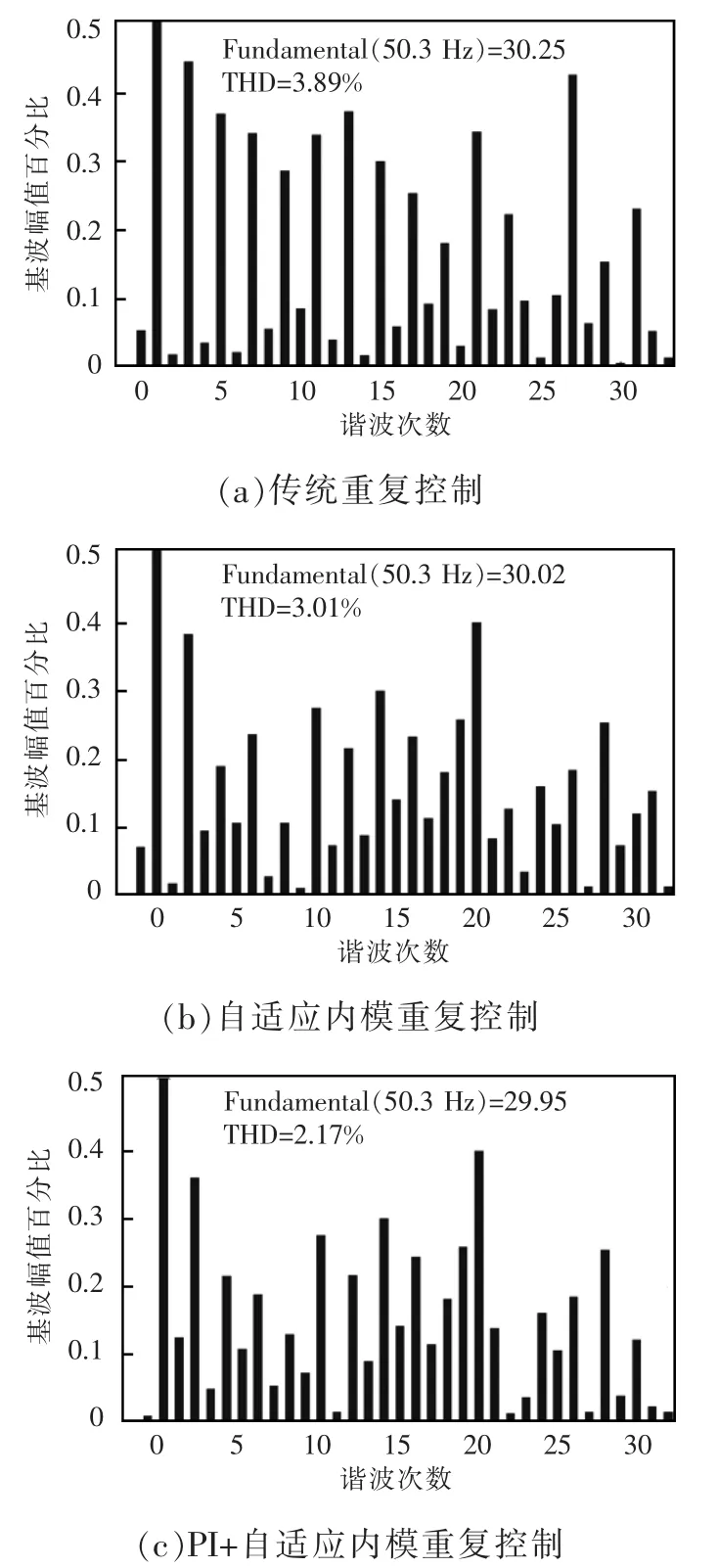
图10 A相输出电流谐波畸变率Fig.10 THD of phase-A output current
我国对新能源并网电流谐波的要求如表1所示。由表1可以看出,我国要求新能源发电并网逆变器输出电流的谐波总畸变率低于5%。比较图10可以看出,当电网频率为50.3 Hz时,基于传统重复控制下的A相输出电流THD=3.89%;基于自适应内模重复控制下的A相输出电流THD=3.01%,比传统重复控制下的A相输出电流THD降低0.88%;基于PI+自适应内模重复控制下的A相输出电流THD=2.17%,比传统重复控制下的A相输出电流THD降低1.72%。由此可得,传统重复控制抗电网频率扰动能力较弱,自适应内模重复控制和PI+自适应内模重复控制抗电网频率扰动能力均较强,抗电网频率干扰能力主要依靠自适应内模,而不是PI控制。

表1 我国对新能源并网电流谐波的要求Tab.1 Requirements for harmonics in grid-connected current of new energy sources in China
3.2 动态性能的仿真验证
为了验证本文所提方案的动态性能,设电网频率为50.3 Hz,由满载突变为半载运行时,基于传统重复控制、自适应内模重复控制和PI+自适应内模重复控制3种方法下的A相输出电流动态波形如图11所示。
比较图11可以看出,当系统运行至0.08 s由满载突变为半载运行时,传统重复控制下的A相输出电流的调节时间为24 ms,自适应内模重复控制下的调节时间为24.5 ms,PI+自适应内模重复控制下的调节时间为18.5 ms。由此可以得出:自适应内模重复控制只是对传统重复控制的内模进行改进,由于需要实时在线计算内模参数,动态响应时间相对于传统重复控制增加了0.5 ms,动态特性没有改善;PI+自适应内模重复控制在自适应内模重复控制的基础上结合了PI控制,显著提高了组合系统的动态特性,且在参考指令电流中加入延迟环节,抑制了组合控制系统由于时序不同而造成的控制耦合,在负载突变时,输出电流没有出现周期性畸变。说明PI+自适应内模重复控制不仅能提高系统的动态响应速度,而且消除了PI控制器与自适应内模重复控制器之间的控制耦合。
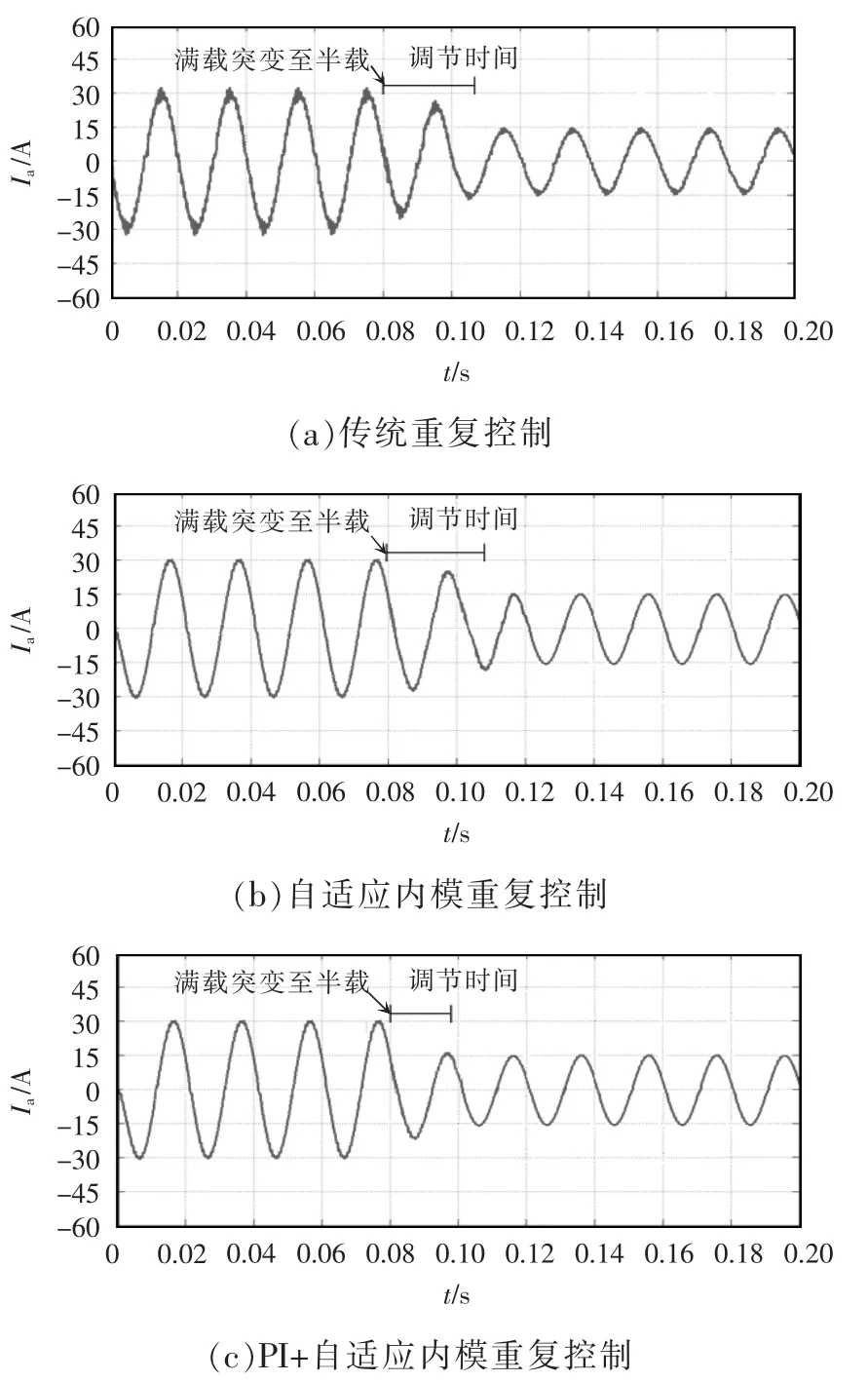
图11 A相输出电流动态波形Fig.11 Dynamic waveforms of phase-A output current
4 实验分析
为了验证PI+自适应内模重复控制的动态性能,搭建了DSP+FPGA的LCL三相逆变器实验平台,其中DSP选择TI公司的TMS320F28335,FPGA选择Xilinx公司的Spartan-7以及相关外围电路,IGBT选择Infineon公司的K40T120,示波器选择Tektronix公司的MDO4104B-3型示波器,实验参数与仿真参数相同。
4.1 抗电网频率扰动性能实验验证
设电网频率为50.3 Hz,满载运行时,传统重复控制、自适应内模重复控制和PI+自适应内模重复控制下的A相输出电流实验波形如图12所示。
从图12可知,当电网频率为50.3 Hz时,传统重复控制下的A相输出电流正弦波形的纹波较为严重,正弦特性较差;自适应内模重复控制和PI+自适应内模重复控制下的A相输出电流正弦波形得到了明显改善,从而验证了抗电网频率扰动能力只与自适应内模有关,而与PI无关的仿真结论。A相输出电流谐波畸变率实验波形如图13所示。
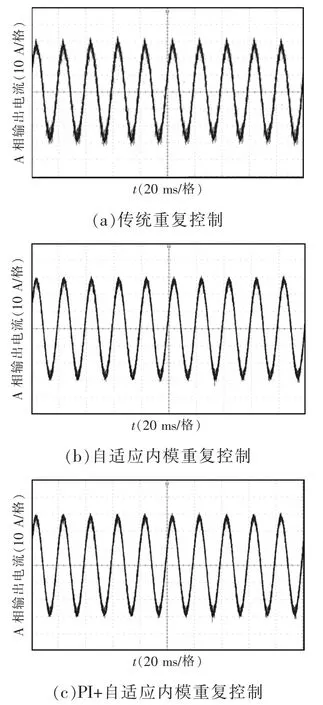
图12 A相输出电流实验波形Fig.12 Experimental waveforms of phase-A output current
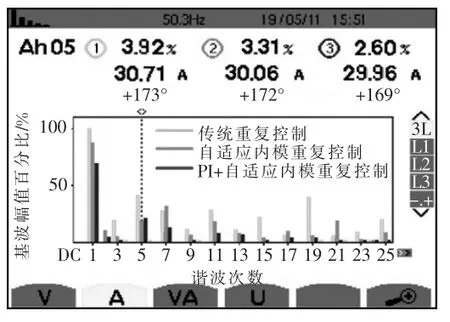
图13 A相电流谐波畸变率实验对比波形Fig.13 Phase-A current harmonic distortion rate experimental comparison waveform
由图13可以看出,当电网频率为50.3 Hz时,基于传统重复控制下的A相输出电流THD=3.92%;基于自适应内模重复控制下的THD=3.31%;基于PI+自适应内模重复控制下的THD=2.60%,与仿真相比,谐波畸变率THD有所增加,但增加幅度不大,主要是实验过程中存在误差造成的。
4.2 动态性能实验验证
设电网频率为50.3 Hz,当系统由满载突变为半载运行时,基于传统重复控制、自适应内模重复控制和PI+自适应内模重复控制3种控制策略下的A相输出电流动态实验波形如图14所示。
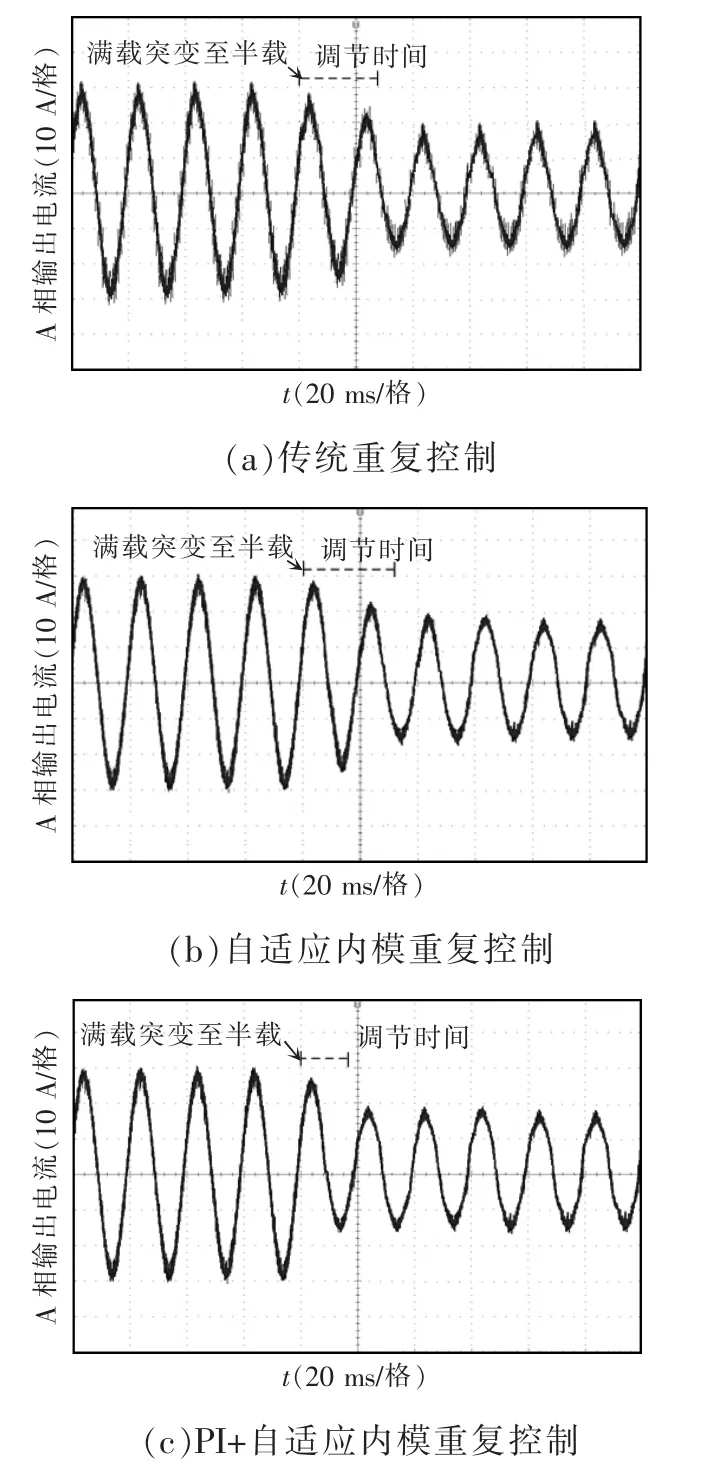
图14 A相输出电流动态实验波形Fig.14 Waveforms of phase-A output current in dynamic experiment
由图14可以看出,传统重复控制下的A相输出电流的调节时间为26 ms,自适应内模重复控制下的调节时间为27.5 ms,PI+自适应内模重复控制的调节时间为20 ms,波形未出现周期性畸变。
由此可得,相比于传统重复控制和自适应内模重复控制,PI+自适应内模重复控制不仅消除了组合控制系统的控制耦合问题,而且有效提高了系统的动态特性。
5 结语
本文在充分研究传统重复控制的基础上,对重复控制内模进行优化,提出一种自适应重复控制内模,可以在电网频率发生波动时,保证良好的抗电网频率干扰能力。此外,由于重复控制动态特性并不理想,将PI与自适应内模重复控制进行结合,提高了组合控制系统的动态响应速度,通过对参考指令电流进行改进,消除了2个控制器之间的控制耦合,解决了负载突变时,输出电流周期性畸变的问题,提高了PI+自适应内模重复控制抗电网频率干扰能力和动态控制性能。

