多无人机绳索悬挂协同搬运固定时间控制

刘 亚，黄攀峰，张 帆

(1.西北工业大学航天学院智能机器人研究中心，西安 710072； 2.西北工业大学航天飞行动力学技术重点实验室，西安 710072)

0 引言

多旋翼无人机具有机动性强、可垂直起降、价格低廉等优点，近年来被广泛应用于远程监视、影视拍摄、资源探测和民用物流等领域。受到军用无人直升机绳索悬挂负载搬运以及救援的启发，提出了旋翼无人机绳索悬挂式搬运系统。考虑到单个旋翼无人机的载荷能力有限，开展了多无人机协同搬运系统的研究，主要有刚性抓取式和系绳悬挂式两种协同搬运连接方式[1]。相比于刚性抓取式，系绳悬挂式能够保留无人机的高机动性以及提高载荷能力的使用效益。针对单无人机系绳悬挂式搬运的系绳摆动问题，设计了依赖系绳或载荷实时状态信息的摆动抑制控制器[2]，使得多无人机协同搬运能够有效抑制系绳摆动，因此多无人机协同搬运受到了研究人员的广泛关注。但是，系绳悬挂式系统是一个欠驱动、非线性耦合系统，悬挂跟踪控制是一个具有很高挑战性的问题。

文献[3-4]中，基于拉格朗日建模法推导了任意数量无人机系绳悬挂式协同搬运系统的动力学模型，并设计了几何非线性控制器，实现了载荷的稳定跟踪控制。但是设计的控制器是集中式的，且需要载荷的状态信息，这种控制方法在缺少测量系统的室外环境下应用具有局限性。基于无人机系绳悬挂式协同搬运系统的微分平坦性，文献[5]利用平坦输出的高阶微分信息对系统开展了轨迹规划和动力学控制研究。系统的微分平坦性对外界扰动、参数不确定以及系统未建模动态具有很强的敏感性，是一种理想条件下存在的性质。文献[6]中，建立了无人机和悬挂载荷之间的正运动学关系，通过无人机的跟踪控制实现了载荷的间接轨迹跟踪。文中假设系绳拉力的实际值与期望值一致，忽视了无人机与载荷之间通过系绳连接的耦合动力学的影响。文献[7]基于凯恩法建立了系统的耦合动力学模型，设计了无人机状态反馈轨迹跟踪控制方法。但是基于该方法，无人机协同搬运系统只能完成定高和匀速运动这种简单的轨迹跟踪任务。考虑系统准静态条件下的运动，文献[8]对无人机系绳悬挂式协同搬运系统的轨迹规划和动力学控制问题展开了研究，但是忽视了载荷的动态特性。同样地，文献[9-10]研究了多无人机协同搬运的跟踪控制问题，但设计的控制方法只适用于系统的准静态运动，忽视了悬挂载荷的动态特性。

在室外条件下，很难测量多无人机悬挂式协同搬运系统的悬挂载荷状态信息，传统的集中式控制方法不利于多体系统提升自主性，且搬运过程中准静态运动不能有效覆盖系统的动态运动场景。因此，本文研究了一般动态场景下，多无人机系绳悬挂式协同搬运系统的轨迹规划和运动控制问题。首先计算了系统的有效旋量空间，并分析了旋量空间与系统构型和运动加速度之间的关系。其次规划了载荷与无人机的可行运动轨迹，满足系绳张紧状态要求且避免了无人机之间的碰撞。最后设计了固定时间跟踪控制器，实现了对期望轨迹的快速稳定跟踪。

1 有效旋量空间分析

1.1 系统平衡方程

多无人机绳索悬挂式协同搬运系统由N个无人机、悬挂载荷(本文研究质点模型)和连接无人机与载荷的系绳构成，如图1所示。

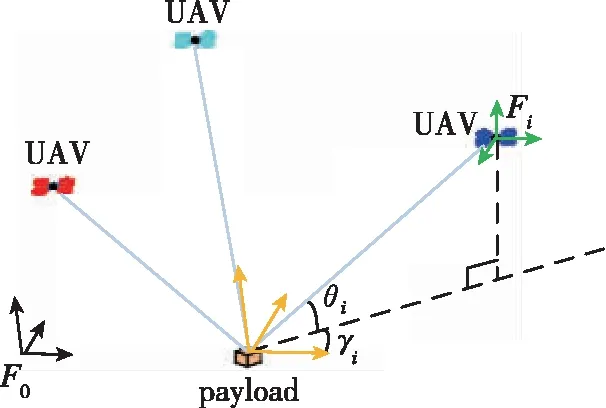
图1 多无人机绳索悬挂式协同搬运系统坐标系Fig.1 Coordinate system of multiple UAVs tether suspended cooperative transportation system

根据牛顿-欧拉定理，动力学方程为

(1)

式中，mp为载荷的质量；rp为载荷在惯性系F0下的位置；g为重力加速度；e3为z轴方向的单位向量；Ti为系绳i的拉力；qi为沿载荷到无人机i的系绳i的方向向量；N为无人机数量。无人机i的平动动力学方程为

(2)

式中，mi为无人机i的质量；ri为无人机i在惯性系F0下的位置；fi为无人机的升力；Ri为无人机本体系Fi到惯性系F0的旋转矩阵。

1.2 有效旋量空间

悬挂载荷是一个无主动控制的一般性物体，通过多系绳拉力提供任务空间旋量，对载荷实施被动控制，系绳拉力由无人机相对载荷的运动产生。因此，系统任务空间旋量由无人机升力空间到系绳拉力和系绳拉力到任务空间2个映射确定。无人机升力空间为

H={f∈RN:fmin≤f≤fmax}

(3)

式中，f=[f1,f2,…,fN]T、fmin=[f1min,f2min,…,fNmin]T、fmax=[f1max,f2max,…,fNmax]T，fimin和fimax分别是无人机i升力允许的最小值和最大值，fimin保证无人机在空中悬停，fimax由无人机执行机构自身决定。拉力空间是系绳可行拉力构成的集合，表示为

T={T∈RN:Tmin≤T≤Tmax}

(4)

式中，T=[T1,T2,…,TN]T、Tmin=[T1min,T2min,…,TNmin]T、Tmax=[T1max,T2max,…,TNmax]T，Timin和Timax分别是系绳i拉力允许的最小值和最大值，Timin保证系绳处于张紧状态，Timax由系绳本身属性和无人机共同决定。本研究中假设系绳本身的强度足够，则系绳拉力允许的最大值Timax由无人机的运动和无人机允许的最大升力决定，根据无人机动力学可得

(5)

因此，系绳拉力与无人机推力之间的关系为

(6)

其中

(7)

根据式(6)可知，系绳i允许的最大拉力由无人机i的最大推力决定，则最大拉力Timax为

(8)

考虑准静态条件下，系绳i允许的最大拉力为

(9)

系绳拉力构成的系统有效旋量空间表示如下

(10)

其中

ΔTi=Timax-Timin

(11)

式中，w为有效旋量集中的元素；d为任务空间的维度；矩阵W=[q1,q2,…,qN]。通过式(10)得到，系绳拉力构成的有效旋量空间是一个凸包。

1.3 系统鲁棒性分析

根据1.2节分析可知，任务空间的有效旋量集取决于无人机的运动加速度、最大升力以及系统构型(系绳方向)。本节分析了无人机运动加速度以及系统构型对有效旋量空间的影响，以及系统搬运不同载荷时的鲁棒性。首先，介绍了一个衡量多无人机绳索悬挂式协同搬运系统鲁棒性的指标——拉力容许裕度γ。拉力容许裕度表示载荷的重力旋量属于有效旋量集合时，重力旋量距离有效旋量空间边界的最小值。拉力容许裕度越小，表示对应的系统容许的最大机动加速度越小，以及载荷能承受的外界扰动越小，则系统的鲁棒性越差。

考虑3架无人机协同搬运情况下，系绳不同面外角θi对有效旋量空间的影响，以及不同质量的载荷重力旋量与有效旋量空间的几何关系。系绳长度为1.5m，无人机质量为1kg，无人机允许的最大升力为18N，保持系绳张紧需要的最小预紧力为0.1N，3架无人机均匀分布在载荷周围，面内角为C2=[γ1,γ2,γ3]=[0,2π/3,-2π/3]，针对不同的面外角C1=[θ1,θ2,θ3]，系统的有效旋量空间与载荷的重力旋量关系如图2所示。图2中，黑色六面体表示系统的有效旋量空间，不同颜色的小球是以对应的载荷重力为球心，拉力容许裕度为半径。小球在六面体内表示系统在静平衡状态下能搬运对应质量的载荷；反之，表示系统在静平衡状态下不能搬运对应质量的载荷。通过图2可以看出，随着系绳面外角C1=[θ1,θ2,θ3]的减小，系统所能搬运的载荷质量上限在下降。在系统能够承受的质量范围内，质量过小，容易导致搬运过程中系绳出现松弛；质量过大，系统允许的最大加速度减小且鲁棒性降低，在外界扰动作用下系统容易出现不稳定现象。所以，对于具体的多无人机悬挂式协同搬运系统，确定系统构型以及搬运载荷范围是具有实际应用价值的。

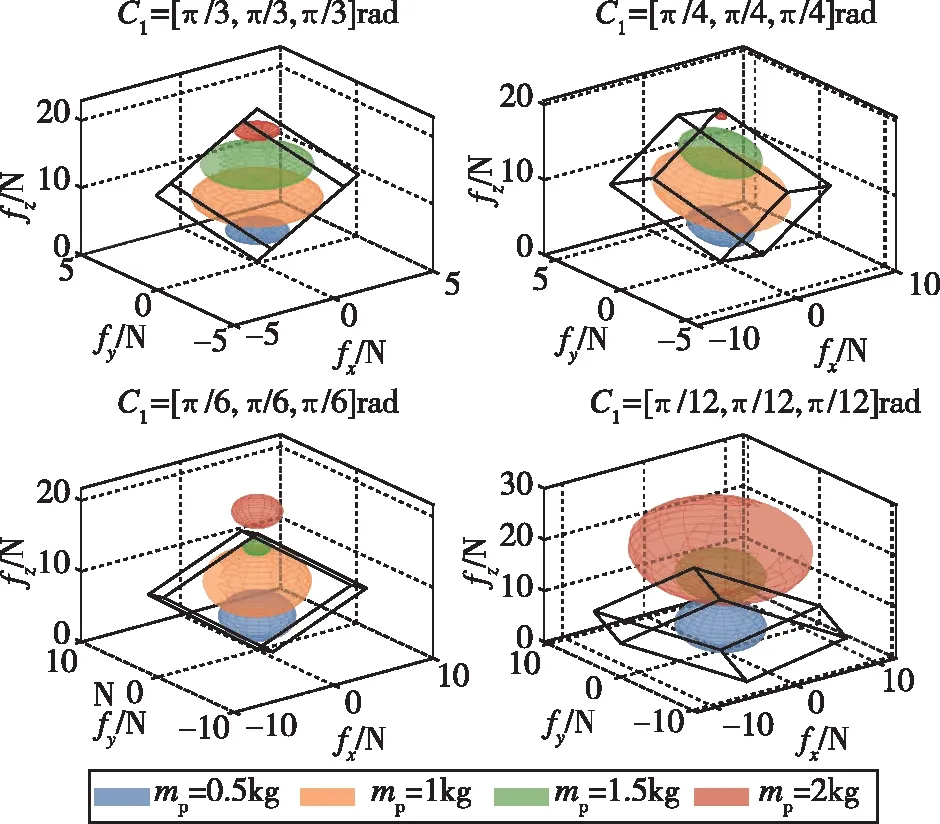
图2 系统不同构型下有效旋量空间与重力旋量几何关系Fig.2 Geometric relationship between effective wrench space and gravity wrench space under different configuration

考虑系统在不同机动加速度下对有效旋量空间的影响，以及不同质量的载荷重力旋量与有效旋量空间的几何关系。系绳长度为1.5m，无人机质量为1kg，无人机允许的最大升力为18N，保持系绳张紧需要的最小预紧力为0.1N，3架无人机均匀分布在载荷周围，面内角为C2=[γ1,γ2,γ3]=[0,2π/3,-2π/3]，根据以上分析，选取面外角为C1=[θ1,θ2,θ3] =[π/3,π/3,π/3]，每架无人机加速度相等，都沿着x轴方向，在不同加速度条件下，系统的有效旋量空间与载荷的重力旋量关系如图 3所示。由图3可以看出，随着加速度的增大，系统所能承受的最大载荷质量上限在下降，主要原因是系统沿着加速度方向不能提供足够的旋量稳定载荷。因此，系统机动加速度越大，系统能搬运的载荷质量越小。同时，观察图3发现，x轴方向加速度越大，系统沿该方向的拉力容许裕度越小，因此系统运动鲁棒性越差。

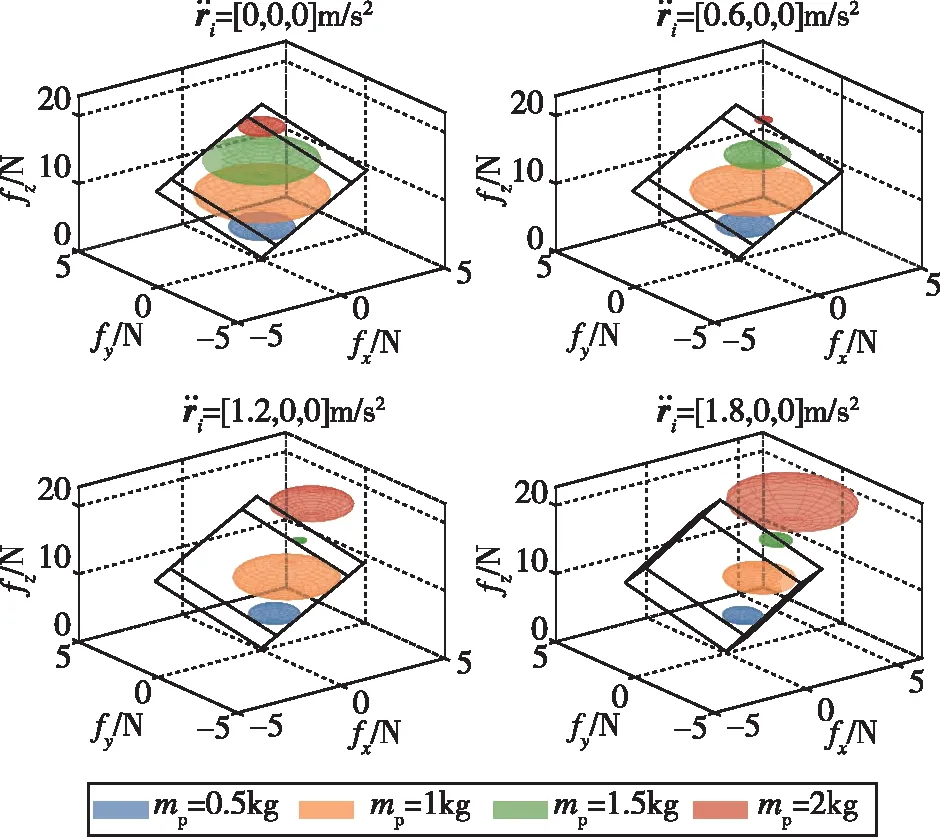
图3 系统不同加速度下有效旋量空间与重力旋量几何关系Fig.3 Geometric relationship between effective wrench space and gravity wrench space under different acceleration

2 系统轨迹规划

2.1 载荷轨迹规划

本文研究问题归纳为：通过对无人机施加主动控制，实现搬运载荷跟踪期望轨迹的跟踪控制问题。对于一个给定的多无人机悬挂式协同搬运系统，已知载荷需要经历的航迹点，首先需要解决的问题是规划出载荷的轨迹。

根据文献[5]可得，多无人机系绳悬挂式协同搬运系统是一个微分平坦系统，通过优化载荷轨迹使其6th导数最小，可以得到最小化snap的无人机期望轨迹，使无人机运动平滑且节省能量。载荷轨迹规划类似于无人机航迹规划，参考文献[12]中无人机航迹规划方法，规划载荷经历约定航迹点的最优轨迹。假设载荷轨迹的m+1个航迹点为rp0,rp1,…,rpm。选取n阶分段多项式函数作为载荷的轨迹函数，具有如下形式

(12)

最优规划问题即是最小化载荷轨迹rp(t)的6th导数平方的积分，规划问题表达如下

(13)

此优化问题可以整理为二次规划问题，形式如下

(14)

二次规划问题是一个成熟的线性优化问题，采用MATLAB中的Quadprog函数对上文二次规划问题进行求解，可得到载荷6th导数平方积分最小的轨迹。值得注意的是，根据1.2节分析可知，系绳施加在载荷上的旋量是有限的，规划问题并没有将该约束问题考虑在内。因此，规划得到的载荷期望加速度可能会违反旋量约束。本文通过增加2个航迹点之间的时间间隔，减小载荷期望轨迹的速度和加速度，直到满足旋量约束为止，得到了载荷的期望轨迹为rpd。

2.2 无人机轨迹规划

根据2.1节中规划的载荷轨迹，求解无人机的期望轨迹，实现通过无人机轨迹跟踪间接控制载荷跟踪期望轨迹的目的。假设2.1节求解的载荷期望轨迹为rpd,根据式(1)求得载荷运动期望旋量为

(15)

期望旋量由系绳拉力提供，表达如下

ωp=WT

(16)

针对质点型载荷，当系统中不共面张紧系绳不少于3根时，载荷的位置可以通过无人机位置唯一确定。本文研究的多无人机系绳悬挂式协同搬运系统的无人机数量不少于3架。因此，式(16)是一个不定方程组。希望找到一组最优或者次优的可行解，使得系绳总拉力最小，以减小对无人机的干扰。拉力优化问题描述为

(17)

式中，φ是避免无人机之间碰撞而规定的2根系绳之间允许的最小夹角。该优化问题利用MATLAB中的fmincon函数进行求解，得到每根系绳的拉力方向qi，再根据系统的运动学关系rid=rpd+Liqi，求得每架无人机的期望轨迹rid。

3 系统动力学与控制律设计

3.1 系统动力学

载荷和无人机的平动动力学如式(1)和式(2)，其中旋转矩阵Ri为

(18)

其中，sφ和cφ分别是sinφ和cosφ的简写，φi、θi和ψi分别是无人机i的滚转、俯仰和偏航角。假设系绳连接在无人机的质心处，无人机的转动动力学在整个系统中处于解耦状态。因此，ith无人机的转动动力学方程为

(19)

式中，li为电机中心到ith无人机本体系Fi原点之间的距离；u2i、u3i和u4i分别为无人机姿态控制3个方向的输入；Ixi、Iyi和Izi分别为无人机沿本体系3个方向轴的转动惯量。无人机的跟踪控制采用内外环的双环控制模式，外环为位置控制环，使无人机实现对期望轨迹的跟踪，并且产生内环的期望姿态信号；内环为姿态控制环，实现外环期望的升力指向。根据式(2)和式(18)，可以得到内环跟踪指令

(20)

式中，fi,d、φid、θid和ψid分别为fi、φi、θi和ψi的期望值；ui=fiRie3=[uxi;uyi;uzi]。

对于一个多无人机系绳悬挂式协同搬运系统，所有无人机通过系绳与一个共同的载荷相连。因此，式(1)和式(2)中的系绳拉力项Tiqi是一个与无人机和载荷运动参数都相关的高度非线性动态函数。为了后续仿真研究，需要计算系绳拉力Tiqi。这种多体耦合系统产生的内部系绳拉力可以利用Udwadia-Kalaba方程进行计算[11]。首先，ith无人机和载荷之间通过系绳i连接，因此他们之间存在如下运动学约束

(21)

式中，rp,i=ri-rp；Li是系绳i的长度。对式(21)进行二次微分得到

(22)

(23)

因此，总的系绳拉力可以表示为

(24)

式中，T=[T1q1;…;TNqN;ΣTiqi]，M=diag[m1,…,mN,mp]，A=[A1;…;AN]，b=[b1;…;bN]，⨁表示直积运算，(*)+表示Moore-Penrose伪逆。但是，由于数值积分运算存在累积误差，仿真中系绳实际长度存在漂移，即

(25)

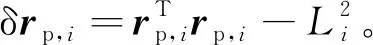
(26)

式中，α和β是反馈增益。把式(26)代入式(24)，得到

(27)

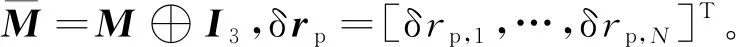
3.2 控制器设计

外环控制器设计使得无人机跟踪期望轨迹。实际任务中，对完成任务的时间有很高的要求，且无人机系绳悬挂式协同搬运系统本身是一种高度非线性和欠驱动的系统。因此，采用有限时间收敛的控制算法提高系统的跟踪鲁棒性具有实际意义。固定时间控制算法是一种特殊的有限时间收敛算法，除继承了有限时间收敛的全部优点外，还避免了有限时间收敛在远离平衡点处收敛速度慢以及收敛时间与初始状态有关等缺点[14]。本文设计了一种新的固定时间收敛控制算法，基于积分滑模和齐次性原理，该算法不仅全局有限时间收敛，同时还避免了滑模控制的抖振问题。设计积分滑模面si为

(28)

式中，vi0为ith无人机的真实初始速度；vid为期望速度；vid0为期望速度的初始值；u0i为待设计的名义控制项。设计具有全局鲁棒性的积分滑模控制项usti为

(29)

式中，μ、λ、η是正的反馈增益；p是大于1的正数。名义控制项u0i设计为

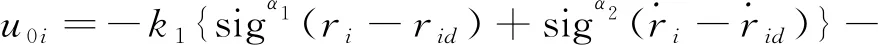
(30)

式中，k1、k2、α1、α2、β1和β2为正实数，且

(31)

综上，无人机外环控制设计为

ui=mi(usti+u0i+ge3)

(32)

无人机内环姿态控制采用基于齐次性原理的固定时间控制方法，设计如下

(33)

(34)

(35)

式中，kp和kd表示正的反馈增益。

3.3 稳定性分析

本节在证明系统闭环稳定性之前，给出了固定时间稳定的概念。

定义1[14]：如下系统

(36)

如果该系统是全局有限时间稳定(globally finite-time stable)且收敛时间函数T(x0)是有界的，存在Tmax>0使得T(x0)≤Tmax对任意x0都满足。那么，系统的原点是固定时间稳定(fixed-time stable)的。

定理1：无人机系统在控制器(32)～(35)作用下，外环轨迹和内环姿态跟踪都能实现有限时间收敛，且收敛时间上界与初始条件无关，仅取决于控制器的参数。

证明：每架无人机的稳定性证明类似，本文证明ith无人机的闭环稳定。首先对积分滑模面si求导得到

(37)

进一步得到

(38)

其中，di=-Tiqi/mi。类似文献[15]中定理2的证明，当控制器参数满足如下条件

(39)

系统的状态量si和ζi收敛到原点，收敛时间的上界是一个与控制器参数有关的常数，即系统固定时间收敛。收敛时间Tr满足如下关系

(40)

其中

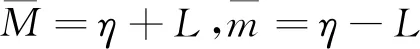
(41)

κ>0，且当κ满足如下关系时，收敛时间Tr的上界最小

κ=(n1/4μ/λ)2/(2p+1)

(42)

当时间大于Tr时，无人机状态到达积分滑模面，且之后一直保持在滑模面上运动，无人机的平动动力学变为

(43)

根据文献[16]中的基于固定时间齐次性原理，系统在控制器的作用下是固定时间稳定的，收敛时间Ts满足不等式

Ts≤2/(kv(1-η1))+2/(kv(η2-1))

(44)

式中，参数kv、η1和η2的定义可在文献[16]中得到。综上所述，无人机在有限时间Tr+Ts内跟踪上期望轨迹，且收敛时间的上界与初始条件无关，仅取决于控制器参数。同理，基于固定时间齐次性原理，无人机内环姿态控制是固定时间收敛的，即无人机在固定时间内跟踪上期望姿态。

4 仿真验证

为了验证提出的轨迹规划和跟踪控制算法，本节分别对3架和10架无人机系绳悬挂式协同搬运系统进行了仿真验证。

4.1 3架无人机协同搬运

3架无人机协同搬运系统参数如表1所示。给定4个载荷的期望航迹点：rp1=[0;0;1]m,rp2=[10;0;1]m,rp3=[10;10;1]m,rp4=[0;10;1]m，经过每个航迹点的时刻分别为0s, 5s, 10s, 15s。根据本文提出的载荷轨迹规划方法，得到载荷经过4个航迹点的最优轨迹如图4所示。控制器参数选取：μ=1，λ=1，η=2，ρ=1.5，k1=2，k2=1，α1=1/2，α2=2/3，β1=3/2，β2=6/5，kp=2，kd=1。3架无人机的期望偏航角为ψid=0，i=1,2,3。悬挂载荷的初始位置为[-1;1;1] m，初始速度为[0;0;0] m/s。3根系绳初始时刻方向为：[0;1/sqrt(3);sqrt(2/3)], [-1/2;-1/(2sqrt(3));sqrt(2/3)], [1/2; -1/(2sqrt(3));sqrt(2/3)]。

表1 系统参数

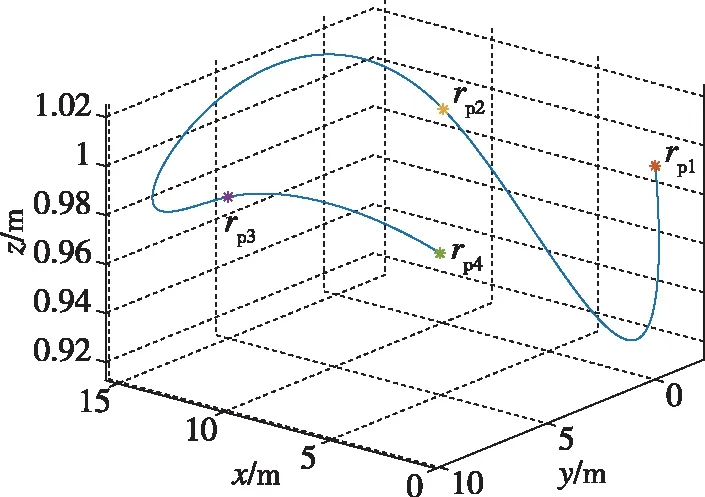
图4 经过4个航迹点的悬挂载荷最优轨迹Fig.4 Optimal trajectory of payload passing through four track points

基于本文设计的控制器，系统状态跟踪曲线如图5～图7所示。图5表示3架无人机跟踪期望轨迹误差曲线，仿真结果表明，设计的无人机轨迹跟踪控制器能够实现无人机轨迹的快速高精度跟踪。图6表示3架无人机期望姿态与实际姿态曲线，可以看出无人机始终处于一个小角度范围的姿态机动，避免了无人机大角度机动造成失稳等现象，所以设计的算法具有可实施性。基于姿态控制器(33)～(35)，无人机能够实现姿态的快速稳定跟踪。图7表示3架无人机协同搬运的悬挂载荷的轨迹跟踪误差曲线，表明在无载荷主动控制的情形下，基于本文提出的轨迹规划和无人机姿轨控制方法，仍然能够实现悬挂载荷轨迹的稳定跟踪控制。对比图5和图7可以看出，悬挂载荷跟踪期望轨迹过程中振动超调量大于无人机，这是因为载荷是通过被动控制来实现轨迹跟踪的。图8所示为无人机系绳悬挂式协同搬运系统3D图。

4.2 10架无人机协同搬运

10架无人机协同搬运系统悬挂载荷质量为mp=5kg,初始时刻10架无人机均匀分布在半径为R=2m的圆周上，相邻系绳之间的夹角为15°，无人机之间避碰允许的系绳最小夹角为φ=10°，由几何

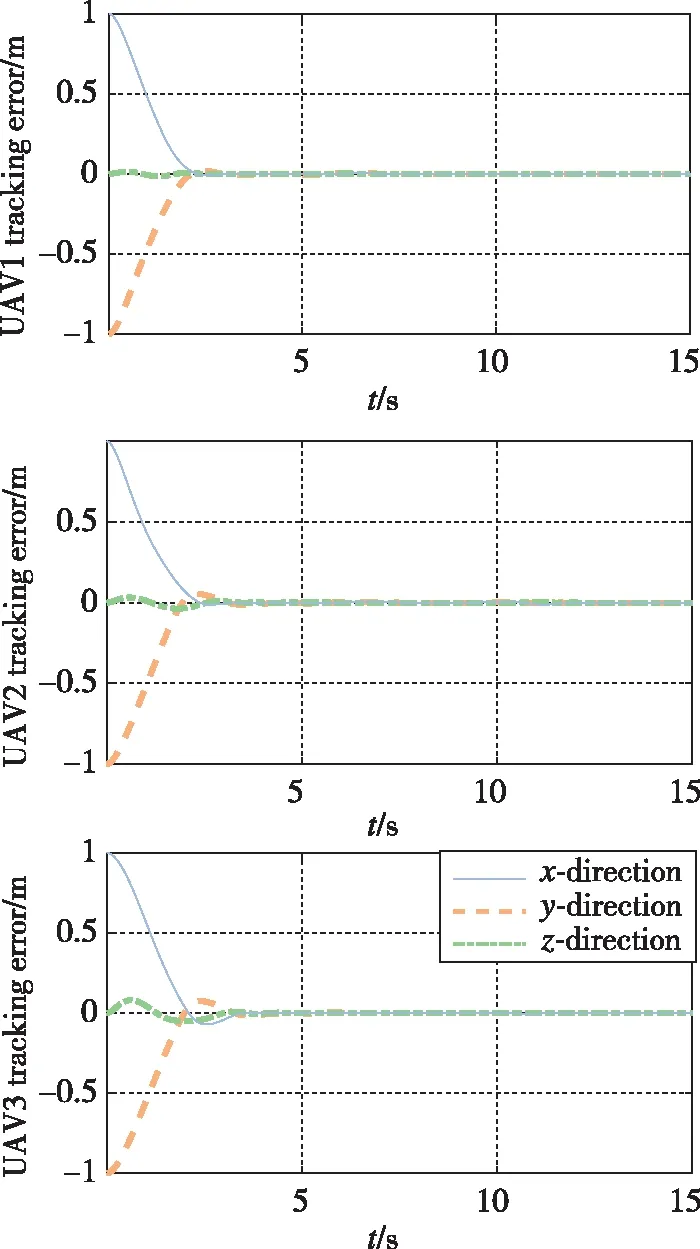
图5 3架无人机轨迹跟踪误差曲线Fig.5 Trajectory tracking errors of three UAVs

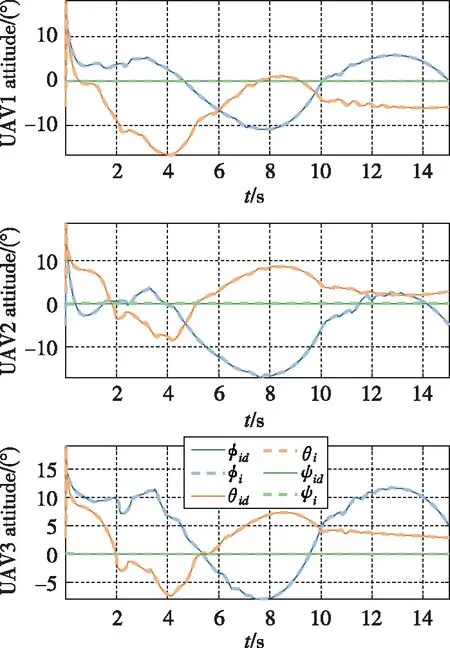
图6 3架无人机姿态跟踪误差曲线Fig.6 Attitude tracking errors of three UAVs

图7 3架无人机协同搬运载荷轨迹跟踪误差曲线Fig.7 Trajectory tracking errors of payload with three UAVs cooperative transportation

图8 3架无人机系绳悬挂式协同搬运系统3D图Fig.8 3D view of tether-suspended cooperative transportation of three UAVs

关系计算系绳长度为Li=Rsin(pi/10)/sin(φπ/360)，无人机参数与3架无人机协同搬运相同，如表1所示。悬挂载荷的轨迹规划也同4.1 节。仿真结果如图9和图10所示。10架自重1kg的无人机能够实现协同搬运5kg的载荷，在设计的内外环固定时间控制作用下，载荷能够稳定跟踪期望轨迹，证明了设计算法的有效性。

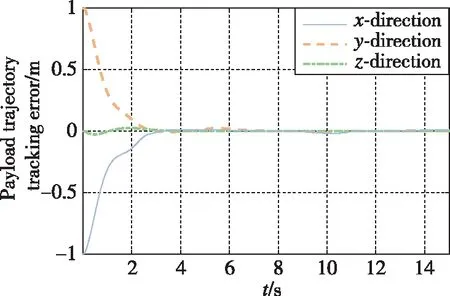
图9 10架无人机协同搬运载荷轨迹跟踪误差曲线Fig.9 Trajectory tracking errors of payload with ten UAVs cooperative transportation

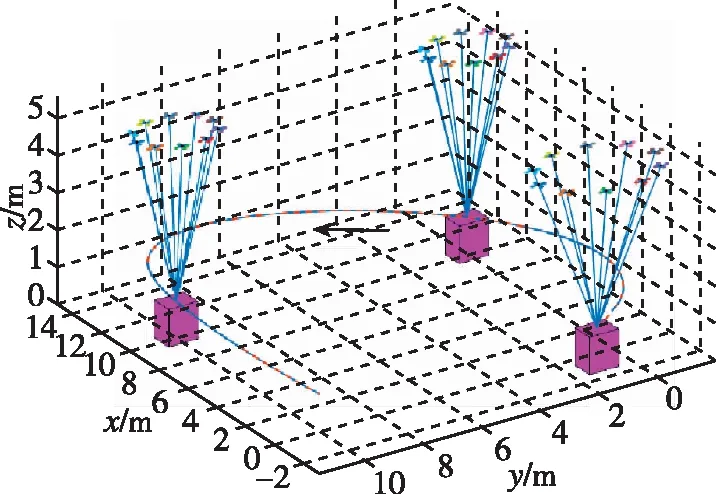
图10 10架无人机系绳悬挂式协同搬运系统3D图Fig.10 3D view of tether-suspended cooperative transportation of ten UAVs

5 结论

本文针对多无人机系绳悬挂式协同搬运系统跟踪控制问题，分析了系统动态旋量空间，规划了载荷与无人机的可行运动轨迹，提出了一种固定时间快速稳定跟踪控制算法。仿真结果表明：

1)系统构型和运动加速度影响载荷旋量空间的大小。本文首次分析了系统动态旋量空间，研究了系统构型、运动加速度与载荷旋量之间的关系，为后续研究轨迹规划和跟踪控制问题奠定了基础。

2)基于系统微分平坦性，通过优化载荷轨迹使其6th导数最小，得到最小化snap的无人机期望轨迹，使无人机运动平滑且节省能量。仿真结果验证了轨迹规划算法的有效性。

3)本文设计了一种无人机姿轨固定时间跟踪控制算法，实现了无人机对期望轨迹的快速稳定跟踪，同时间接控制悬挂载荷快速稳定跟踪期望轨迹。

本文假设悬挂载荷为质点，忽略了载荷的几何构型与姿态运动，后续研究将考虑一般形状的载荷。