多源信息融合卫星组合导航系统的可观度分析

乔怡群，邱红专，宋 华

(北京航空航天大学自动化科学与电气工程学院，北京 100083)

0 引言

卫星的自主导航是指在不依赖地面站的情况下，通过其自身携带的星载敏感器确定卫星的速度、位置和姿态信息。这种在较长时间内，不依赖地面，只依靠星载敏感器高精度测量来实现卫星定轨的方法，是当前研究的热点问题。

目前，全球四大导航系统有美国的全球定位系统(Global Positioning System，GPS)、欧洲的GALI-LEO、中国的北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)和俄罗斯的GLONASS[1]。这些导航系统可以对卫星进行导航，但是受全球导航卫星系统(Global Navigation Satel-lite System，GNSS)可见性的约束，存在部分时间段内GNSS导航卫星不可见的情况，这将大大增加待导航星的滤波误差。本文研究了基于GNSS、地标矢量和星光矢量的自主导航方法，可以保证在GNSS不可见时的定轨精度。

一般地，分析线性定常系统的可观测度较为容易，而对非线性时变系统的分析则比较麻烦[2]。文献[3]提出了一种利用李导数构造可观测性矩阵的方法，然而该方法对于状态维数较高、非线性程度较强的方程而言，计算量大，实现起来较为困难。文献[4]针对小天体探测器着陆自主导航系统，在文献[5]算法的基础上，利用误差协方差矩阵进行特征值分解，以分析特征值、特征向量与状态可观度的关系，但该方法只能够分析出状态的某一种组合的可观测度。文献[6]提出了不可观度的概念，在构建可观度矩阵时，需要对量测方程矩阵和状态转移矩阵进行变换，计算量较大。文献[7]利用误差椭球分析导航系统的可观度，并根据映射原理计算误差的上界。文献[8]利用奇异值分解(Singular Value Decomposition，SVD)的方法分析系统的可观度,在引入了测量值Z的情况下，可以定性地分析系统状态的可观度。上述方法中对系统可观度的分析往往较容易实现；然而针对系统每一个状态的可观度进行分析，往往实现困难或者难以定量描述。

本文以高轨卫星为对象，研究了基于GNSS、地标矢量和星光矢量的卫星自主导航方法。在此基础上，以基于谱半径的系统可观度分析方法对不同观测量下的系统可观度进行分析[13]；同时，在文献[9]的基础上，针对非线性时变系统的状态可观度进行定量分析，并与滤波精度相结合进行对比分析。

1 组合导航滤波器的状态方程和测量方程

针对高轨卫星的自主导航问题，下面分别给出了系统的状态方程和量测方程。

1.1 系统状态方程

系统的状态变量为

(1)

式中，rx、ry、rz、vx、vy、vz分别为卫星在地心惯性坐标系下的位置和速度。若卫星的摄动仅考虑含J2项的非球形引力摄动[10]，可以列出在地心惯性坐标系下单颗卫星的状态微分方程如下

(2)

1.2 量测方程

本文采用的传感器是GNSS接收机、地标导航敏感器和星敏感器。GNSS接收机提供伪距和伪距率信息，地标导航敏感器提供地标矢量信息，星敏感器提供星光矢量信息，然后利用星光矢量和地标矢量之间的夹角来提供二者角度测量信息。

伪距是GNSS接收机到导航星的一个基本的距离测量值[11]。伪距测量的表达式可以写为

(3)

其中，rxs、rys、rzs为GNSS卫星在惯性系下的位置；ερ为均值为0的伪距测量噪声。

(4)

地球路标导航敏感器提供了一个指向地标的方向矢量[12]，其在机体系(b)下的测量方程为

(5)

其中，rd为地标在惯性系下的位置矢量；εl为均值为0的高斯白噪声。

星敏感器可以提供一个指向遥远恒星的单位星光矢量，星光矢量和地标矢量之间的夹角可以表示为

(6)

其中，us为机体系下的单位星光矢量；εα为均值为0的高斯白噪声。

对于高轨同步卫星，可能会因为地球的遮挡而收不到GNSS卫星的信号，因此测量值矢量的维数取决于可见的GNSS卫星个数。对于确定GNSS卫星可见性的条件，将会在1.3节进行介绍。下面先给出系统的量测方程

(7)

将上面给出的方程进行离散化，即可得到卫星自主导航系统的离散滤波模型。

1.3 GNSS可见性分析

高轨卫星所处的位置在GNSS星座之上，所以接收机可能捕获到的GNSS导航信号只能是来自地球另一面的GNSS卫星。此时由于地球遮挡和GNSS信号在传播过程中的损耗，导致了高轨卫星定轨中面临着可用导航星数目少和信号较弱这2个主要难点。高轨卫星对GNSS的可见性主要取决于几何可见性和信号强度这2个因素。对于高轨卫星来说，只有同时满足以下几个条件， GNSS导航星才是可见的。

几何因素主要考虑的是高轨卫星、GNSS导航星和地球之间的相对位置关系，只有当GNSS卫星信号发射半角满足小于天线发射信号的波束角且高轨卫星不在地球的遮挡范围内时，高轨卫星才有可能接收到导航星的发射信号。

如图1所示，地球的遮挡角为βe，信号波束发射半角为βG，需要满足的条件是

βe<α1≤βG

(8)

其中，α1为OS和SF之间的夹角。

图1 GNSS可见性示意图Fig.1 GNSS visibility diagram

由于导航星发射天线仅能对地播发导航信息，那么只有当高轨卫星接收机的天线指向地心，并且高轨卫星与导航星所呈角度在接收机天线波束宽度范围内时，高轨卫星才可能接收到GNSS卫星的信号。即需要满足关系

α2≤φ

(9)

其中，φ为接收机的波束接收宽度；α2为OF和FS之间的夹角。

GNSS导航卫星发射天线朝向地球，而被测高轨卫星的轨道高度不低于GNSS导航星的轨道高度。因此，高轨卫星只能接收位于地球另一侧的GNSS导航星发射的信号，这样经过远距离传输的信号强度大大减弱，增加了接收难度。

星载GNSS接收机接收信号的功率与导航星发射功率、发射天线增益、链路损耗、接收天线增益等诸多因素有关。根据Friis传输公式，可计算接收信号的功率如下

(10)

其中，Pr为接收信号功率；Pt为载波信号的发射功率；Gt和Gr分别为发射和接收天线的增益；λ为载波信号的波长；d为导航星与接收机的距离。

将式(10)采用分贝表示如下

(11)

2 可观度分析方法

下面对基于谱半径的系统可观度分析方法和基于SVD的可观度分析方法分别进行介绍。

2.1 基于谱半径的系统可观度分析方法

为了描述系统可观测程度，定义系统的可观度[13]为

(12)

式中，ρ(Pk)为系统滤波误差协方差阵Pk的谱半径。可以证明，用谱半径定义的系统能观度和状态估计精度满足如下关系[13]

(13)

式(13)建立了系统状态估计精度与系统可观度之间的关系, 可观度越高则系统的状态估计精度越高。可见, 以谱半径定义的系统可观度能够定量地描述整个系统状态估计的好坏, 而不是某一状态组合的好坏。 因此,谱半径定义的系统可观度是可行的。

2.2 基于SVD的可观度分析方法

对于非线性系统，一般先依次将其线性化和离散化，然后利用线性离散系统的可观测性理论来分析自主定轨系统的可观测性。

对于离散非线性系统

x(k+1)=f(x(k))+wz(k)=h(x(k))+v

(14)

其中，x∈Rn×1，z∈Rm×1，w和v分别为系统噪声和量测噪声，互不相关，且有如下关系

E[w(t)wT(τ)]=Q(t)δ(t-τ)E[v(t)vT(τ)]=R(t)δ(t-τ)

其中，δ(t-τ) 为狄拉克函数。

可以得到可观测性矩阵为[14]

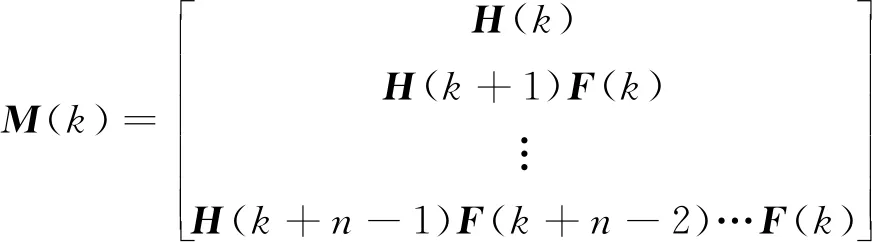
(15)

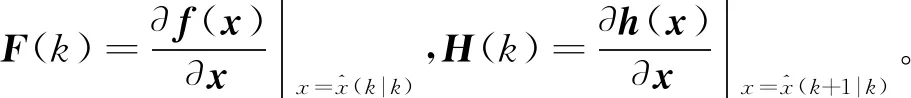
若F(k)和H(k)是定常的，则式(15)就是通常的线性时不变系统的可观性矩阵，文献[9]针对这种系统利用可观测性矩阵建立了状态初值x1和测量值Z之间的关系。与此类似，针对式(16)所示的非线性系统，也可以通过M(k)得到x(k)和测量值Z之间的关系。具体推导过程如下

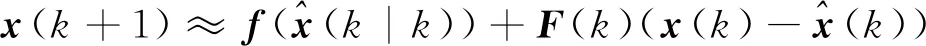
(16)

即

x(k+1)≈F(k)x(k)+u(k)

(17)

同理将量测方程线性化可以得到

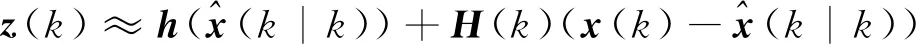
(18)

令

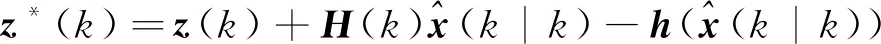
(19)

根据文献[15]中的方法，可以得到

(20)

两边同时乘以Hk+n-1并移项可以得到

Hk+n-1Fk+n-1,kxk=z*(k+n-1)-

(21)

那么有

(22)

其中

(23)

(24)

式中，σ1,σ2,…，σr为奇异值且满足以下关系：σ1≥σ2≥…≥σr>0，由此可以得到

(25)

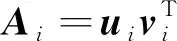
式(24)与文献[9]中的结论类似。文献[9]根据以上关系，给出了一种计算每个状态分量可观度的方法，具体步骤如下：

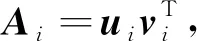
(26)

其中，Aij表示矩阵Ai的第j列元素。通过式(26)即可以确定奇异值σi对应的第j个状态的可观测度，且根据该方法计算得到的各个状态的可观测度都是归一化的非负值，便于比较可观测度的大小。

(27)

本文利用上面的方法，对每个状态分量的可观度进行仿真分析。

3 系统可观度仿真结果与分析

基于第2节的滤波模型(坐标系是J2000地心惯性坐标系)进行仿真,同时利用第3节的可观度分析方法进行系统的可观度分析和状态的可观度分析。图2所示为GNSS可见星数目随时间变化曲线。

从图2可以看出，在30000s附近和67000s附近，GNSS完全不可见;在74000s附近，GNSS可见星数目较多。

图4 速度滤波误差Fig.4 Velocity errors

图3和图4所示分别为卫星利用GNSS、地标矢量和星光矢量导航时的位置误差曲线和速度误差曲线。表1所示为滤波稳定后的导航误差大小和各状态分量的可观度。可以看到对于位置来说，Y轴的可观度最大，其对应的位置误差最小；Z轴的可观度最小，其位置误差最大。对于速度而言，可以得到类似的结论。图5和图6所示分别为利用SVD方法和谱半径方法计算的系统可观度随时间变化曲线。图5和图6比较可知，二者可观度较大的时刻相近。因此，两种定义的方法都可以体现系统的可观度。与图2进行比较可知，在仿真时间30000s和67000s左右时，GNSS可见星数目最少，系统的可观度也较差；在仿真时间74000s左右时，GNSS可见星数目较多，此时的系统可观度较好。由此可知，系统可观度受到GNSS卫星可见星数量的影响较大。

图5 系统可观度随时间变化曲线(奇异值)Fig.5 System observability curve over time(singular value)

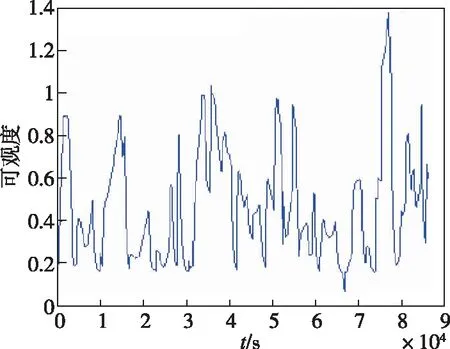
图6 系统可观度随时间变化曲线(谱半径)Fig.6 System observability curve over time(spectral radius)

通过表1分析可知，对状态可观度贡献最大的是GNSS，地标和星光矢量二者对状态可观度的影响很小，这也与上面的分析结果相符。在采用GNSS、地标和星光矢量和地标夹角进行组合导航时，应该将GNSS作为主要的导航手段，另外2个传感器作为辅助手段。

由表2和表3的对比可知，在增加GNSS的数目时，状态的可观度总体上呈增大的趋势，估计误差随GNSS星数目的增加而减小。对每一组仿真而言，位置和速度的误差在x轴上最小，z轴上最大；而状态的可观度大致为x轴上的可观度最大，z轴上的可观度最小。可观度分析结果与滤波结果相吻合。对于地标而言，在增加地标的数目时，状态的可观度总体上呈增大的趋势，估计误差随地标点数目的增加而减小。对一组仿真而言，位置和速度的误差在x轴上最大，z轴上最小；而状态的可观度大致为x轴上的可观度最小，z轴上的可观度最大。这种SVD方法可以粗略地表征状态可观度和滤波误差之间的关系。

表1 导航系统误差大小与可观度大小

表2 不同测量值时的状态可观度

表3 不同观测值时的滤波精度

4 结论

本文利用基于GNSS、地标矢量和星光矢量的高轨卫星组合导航模型进行了可观度分析。算法分析与仿真结果表明：

1)系统可观度最主要的影响因素是GNSS的可见星数目，地标和星光矢量可以作为辅助信息引入，同时有助于提高状态的可观度。

2)基于SVD可观度分析方法可以较好地分析出状态的可观度，同时可以粗略地表征出状态误差的大小。对于同一量纲的状态，计算出的可观度较大时，其滤波误差小且精度高。