基于高性能密码实现的大数据安全研究

李 萍，朱春琴，曹 磊，孙 毅，魏房忠

（江苏省大数据管理中心，江苏 南京 210000）

0 引言

目前，信息技术发展较快，已经步入了人工智能技术时代。人工智能技术的建立主要基于大数据计算。现如今，大数据计算技术取得较快发展，在多种计算模式下，利用大数据处理技术，能在大量而且分散的数据中，及时找出有价值、有意义的数据，促使生产力水平得到显著提高，助推经济发展。

1 大数据安全逻辑架构

如图1所示为逻辑架构，从逻辑上来看，针对大数据安全，可把逻辑结构分为3层。从逻辑架构层中可以得知，密码算法层占据关键的位置，在很大程度上，能为方案奠定有力的技术支撑。数据安全方案中含有多种密码算法，例如大家熟知的SM4-XTS算法，通过密码算法层，都能促使这些算法得到使用。在密码算法层中，应当加大密码技术的研究力度，不断对相关的优化算法进行摸索，例如大整数运算。此外，也不能忽视对众核并行技术的研究，以便在FPGA平台中，使高性能运算得到实现。强化对众核技术的优化，重视对智能协同计算的健全，充分结合并发任务，以便能促使处理阵列得到提升，有效发挥FPGA平台的作用，有助于达到高速密码算法的目标，基于大数据安全方案，保证方案能更好地满足密码运算的要求。对密码服务层来讲，在多数情况下，服务对象往往是算法层，可实现对算法层的封装。在此基础上，能向外部提供接口，积极发挥密码服务层的作用，操作人员能达到自定义指令的目的。在此情况下，能随意使用密码算法层，最终对目标进行服务，比如文件储存加密、身份认证等。对于应用层而言，主要是基于密码服务层，对其接口进行调用，来处理大数据应用问题[1]。在调用储存加密接口之后，能在极短的时间内解密较多的大数据；通过对身份认证接口进行调用，可更好地满足身份认证需求；对模幂运算进行调用，能快速对同台算法进行封装，有效完成业务需求。

2 大数据安全的快速实现

对于大数据安全的快速实现，本文主要从SM4-XTS的快速实现、SM2的快速实现等方面进行分析。

2.1 SM4-XTS的快速实现

SM4实现：在SM4性能影响方面，S-BOX的影响最大。对于S-BOX的实现，主要包括两种方式，一种是基于数个S-BOX，而形成的逻辑方式；另一种是依据ROM的查找表，进而形成的方式。若选取数个S-BOX，那么基于轮函数，可通过组合逻辑方式，不需借对寄存器，往往只需依靠1个时钟周期，就能有效完成迭代过程。另一方面，对于多个S-BOX而言，即便会耗用大多数的资源，然而通过对逻辑的控制，能降低复杂度，更加容易采用流水线处理；若通过一个S-BOX实现，若要达到变换非线性的目的，则需分时复用S-BOX，与此同时，虽然不使用资源，不过在逻辑控制方面，变得更加复杂，需使用到较多的寄存器资源，而且明显提高花费的时间，对于一次迭代的完成，需使用数个时钟周期。基于此，对于组合逻辑实现而言，采用多个S-BOX方式，能实现对流水线方式的支持，仅需一个周期，即可完成整轮函数[2]。

图1 逻辑结构

在SM4密钥拓展方面，使用动态即时轮技术，在任何一个周期中，通过一个单独密钥，来对1个分组进行加密解密，而且对性能不造成影响，可为流水线技术的应用奠定坚实的基础。基于此硬件架构，在性能提升方面，可借助于流水线方式得以实现。采用即时轮拓展技术，在SM4运算方面，在同一时间内，即可以进行加解密运算，也能进行轮密钥拓展。对流水线开展精心设计，在一个周期内，采用一个单独密钥，对一个分组进行加密解密，而且对性能不造成影响。通过这样的方式，能以较少的周期实现对流水线的建立，在流水线被填满之后，基于部分逻辑电路，能促使运算能力得到积极发挥，极大地提高算法性能。基于快速实现方案，采用的流水线技术为32级，使SM4算法得以实现，为SM4-XTS的快速实现，提供了强有力的技术支持。

2.2 SM2的快速实现

对于SM2协议而言，通常可划分为4层，图2为SM2总体架构，顶层为SM2协议，其中包括诸多内容，比如密钥协商、签名以及加解密等，对于全部协议而言，皆依据点乘操作。点乘操作的实现，主要基于两方面，一是倍点运算，二是点加运算。架构底端的运算为算数运算，所包含的运算一共有4种[3]。有效利用一系列的优化策略，能实现加速运算的目的。基于此，不但能极大缩短运算所需要的时间，而且在一定程度上，也能促使性能得到提升。

对模乘器的优化：在全部的算术运算中，对SM2协议来讲，模乘运算占据了重要的位置，在实际应用中，模乘运算使用的频率是最高的，而且对于所有的模块而言，模乘运算是相当重要的，从运算时间上来看，所占的比例高达90%。对模减以及模加运算来讲，所包含的逻辑结构较为简单，在实际应用过程中，使用模逆运算的情况相对较少，并没有得到广泛的利用，所以对于模逆运算的实现而言，有必要对模乘器进行优化。优化策略，主要包括以下几点：借助于DSP运算单元，来对模乘器进行构建。对于DSP而言，主要基于FPGA平台，向其内置的运算单元，对于乘累加运算是支持的。基于DSP，对其进行精心设计并组合，避免主要路径出现延时，可为高速模乘运算，提供强有力的支持。对于模乘运算而言，在对运算时间进行确定的过程中，往往是依据一些积数量。对256b乘法进行构建，在少量加法形成方面，通过Karastusba算法，仅需使用3个128b乘法即可完成，相对于简单乘法，在使用Karastusba算法之后，能极大地降低运算量，通常情况下能减少1/4。通过分而治之方式，对N使用相同的策略，能极大缩短模乘运算时间。

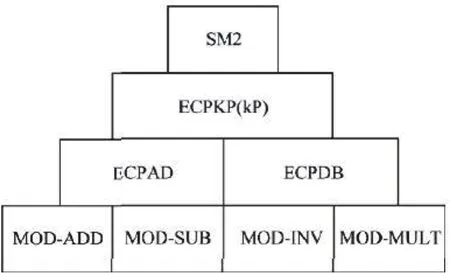
图2 SM2总体架构

充分利用SM2参数，实现对模约减运算的优化。为更好地实现模乘运算，可基于模约减过程，有效结合协议素数，进而能达到这一目的，这主要由于素数P有一定的特殊性。可通过两种方式，得到模约减结果，一种是采用若干次加法，另一种是借助于减法运算[4]。相比于一般的Montgomery算法，可省掉多次乘法运算，而且性能得到显著提高。点加以及倍点的改进：针对倍点与点加，在对两者进行运算时，为避免模逆运算，主要是由于此运算比较耗时，须对坐标进行改变，最终形成雅克比坐标。在SM2协议中，对于倍点而言，需进行四次模减、八次模乘以及六次模加；对于点加而言，需进行六次模减、十一次模乘以及两次模加。在优化策略方面，主要有以下两点：针对模乘器，促使其流水线能力得到积极发挥，进而有助于提升运算效率；充分结合点加与倍点，采取有效手段，尽可能减少模乘的相关性。对于模乘器而言，为更好发挥流水线性能，可有效结合运算公式，全面分析数据的相关性，对计算顺序进行详细的设计，促使模乘运算与模加运算没有数据相关性。点乘的优化：对于签名而言，在所有的操作中，点乘操作是最耗时的，也就是（x1，y1）=[k]G。针对系数k，以二进制的形式，将其展开为1和0的组合，通过NAF编码方式，来实现对系数k的编码，针对点乘系数K，增加其中0的数量，通过这样的方式，在降低运算次数的同时，也能加快签名速度。

2.3 大整数模幂的快速实现

通过同态加密算法，针对数据密文和明文，可保持两者之间的同态关系，其中包括诸多算法。对于全同态算法而言，存在一系列的缺点，比如效果不高、速度较为缓慢、有着很大的密文规模等，在此情况下，业务场景将很难适应；对于一系列的单同态算法而言，比如Paillier算法，在实现上较为简单。单同态算法主要研究的内容是Paillier算法。通常情况下，在Paillier算法中，最为棘手的问题就是模幂问题。模幂运算实质上是大整数的模乘，基于此，对模乘的快速实现进行介绍。图3为大整数模乘算法，借助FIOS实现方式，有助于FPGA的实现。基于此算法，ω为128，也就是128b乘法运算，由此当s为4、8、12以及16时，在模乘运算位方面，长度依次为512、1 024、1 536以及2 048，结合s不同值的解释，由此基于乘器长度，能达到动态配置的目的[5]。

在实现过程中，值得一提的是，对结果储存问题要加以重视。基于1个大整数，若借助于寄存器来保存数据，将会造成资源的大量浪费，在数据宽度加大的同时，针对寄存器，促使其硬件资源显著增加。因此针对M、A、B以及中间结果，可通过BRAM来进行储存，BRAM源于FPGA。通过实验证明，能极大地降低对资源的消耗，大概可降低60%左右，伴随数据宽度的不断加大，效果将会变得更突出。总的来讲，通过模幂处理器可实现动态配置长度。基于FIOS算法，对其进一步优化，并合理应用BRAM，模幂的运算能高速、高效地完成。

3 实验与结果

充分结合FPGA芯片，有助于对密码协处理器的实现，对于该处理器而言，其性能是很强的，具体而言，可为多种密码功能的实现提供强有力的支持，比如模幂运算、SM2签名等。在实际应用过程中，当设置不同的密码之后，能实现对密码功能的调用。对于数据安全方案而言，通过对该处理器的有效使用，在单芯片方面能提供相应处理方案，基于此，可为产品更好地推广发挥一定的促进作用。

3.1 实验环境

借助于KC705开发板，促使各算法得以实现，并对方法进行测试，获取实验数据。对于KC705而言，是一种开发套件，源于7系列的FPGA，对于FPGA芯片来讲，属于XC7L425T-4，源于Kintex-7系列，该系列属于中端系列，在Xilinx公司所有的产品中，该产品有着最高的性价比，有助于对产业进行推广，而且推广价值是很大的。通过对KC705开发板的使用，基于密码协处理器，可为密码运算的实现提供强有力的支持，对3种算法的有关内容进行了优化处理，比如地址分配以及资源共享等，在输入不一样的命令码之后，能实现对有关密码功能的支持。

3.2 实验结果

本方案的执行有助于对密码协处理的实现，具体而言，可为多种密码功能的实现提供强有力的支持，比如模幂运算、SM2签名等。在实际应用过程中，当设置不同的密码之后，能实现对密码功能的调用。在此该处理器中，存在3个密码模块，从功能上来分析，模块之间是没有联系的，是相互独立的；不过从时钟频率上来看，不同密码模块存在一定的差别，所以需要处理异步时钟，与此同时，充分结合算法模块，来分配相应的访问地址。该处理器实验结果如表1所示。

图3 大整数模乘算法

表1 实验结果

从表中的数据可以得知，在资源占有率以及时钟频率方面，这三种算法存在不同。对于SM4-XTS而言，可运行的时钟频率为250 MHz，在对1个SM4分组进行处理时，所需的时间为0.004 μs，在加密性能方面，可达到31.5 Gbps；对于SM2 Signature而言，可运行的时钟频率为150 MHz，在签名速度方面，可达到26 062次/s；对于大整数模幂运算而言，可运行的时钟频率为66 MHz，完成1次模幂运算，所需的时间为149.3 μs，在速度方面，可达到6 702 次/s。如表2所示，针对此密码协处理器，列举了其资源使用情况，在表中LUT为look-up-table的简称，DSP是乘法器，皆属于基本逻辑单元。本方案有效应用了元器件特性，促使各模块实现效率得到提升。从表2中的数据可以得知，本方案是可行的，不仅能实现高性能算法，而且预留了很多的资源，有助于控制逻辑的实现，比如逻辑调度。

表2 资源使用情况（FPGA）

4 结语

通过以上的分析可以得知，对于多个S-BOX而言，虽然占用了大部分资源，然而通过对逻辑的控制，能降低复杂度，更加容易采用流水线处理；在流水线被填满之后，基于部分逻辑电路，能促使运算能力得到积极发挥，极大地提高算法性能。通过实验得知，本方案是可行的，不仅能实现高性能算法，而且预留了很多的资源，有助于控制逻辑的实现。