水泥环参数和套管形状参数对套管强度的影响

宋烨炜，董泽训，李 宽*，孟庆生

（1.中国地质大学（北京），北京100083；2.山东省第六地质矿产勘察院，山东招远265400）

0 引言

目前，随着油气的不断开采，全世界范围内的油田都面临着严重的套管损坏问题。例如，伊拉克的哈法亚油田Yamama 层高温高压，地层水矿化度高，原油溶解CO2含量较高，易形成酸性介质对套管进行腐蚀［1］。胜利油田因油层附近地层倾角大，且发育有地下断层、砂砾岩体，容易引发地层滑移和断层活动，进而造成套管错断、缩径和弯曲等问题［2-4］。大庆油田损坏形式主要为套管变形和套管错断，共发现各类套损井1 万多口，占油水井总数的20%左右［5］。孤东油田属于河流相沉积，油层胶结疏松易出砂，出砂后使油层原来承受的部分重力转移给了套管，致使套管失稳，引起弯曲［6］。辽河油田多为热力采油，在采油过程中，套管上产生了热应力和疲劳应力，最终导致套管损坏［7-8］。克拉玛依油田井下技术状况复杂，因施工等多种原因易造成泥岩吸水蠕变，挤压力不断增大使得套管缩径、错断等［9］。套管损坏既影响了正常的油气开发，又使注采网层系布局越来越不合理［10］。经保守统计，我国目前套管损坏井2.5 万余口，并且正以每年千口以上的数量增长，同时套管损坏井的增长速度有明显的上升趋势。我国石油对外依存度达到了70%～80%，远远超过了国际平均水平，并且各油田每年因套管损坏而造成的经济损失达数十亿元［11］，因此研究影响套管强度的因素对油田的持续发展和国家的能源安全有重大意义。

套管损坏的本质是外荷载超过了套管的极限承载力［12］，因此，通过提高套管的极限承载力可减少部分情况下套管损坏的概率。影响套管抗挤强度的因素多种多样，其中最主要的是非均匀外载、水泥环参数、套管缺陷和射孔等原因［13-19］。本文将对水泥环参数和套管缺陷这两种因素展开详细的研究。在之前国内外学者的研究中，陈占锋等［15］考虑地层非均匀地应力的影响，建立了地层、水泥环和套管的二维有限元模型，Evans 等［16］采用实验室测试或者是有限元分析的方式研究水泥环参数对套管强度的影响，张睿栋［17］、范森等［18］、王国华等［19］研究了套管的椭圆度和偏心率对套管强度的影响，但他们都没有研究水泥环对不同径厚比套管、偏心套管和椭圆套管的影响。本文将通过建立套管和水泥环的三维有限元模型，利用Ansys 有限元分析软件进行求解，并与理论计算结果对比，在不考虑套管内压的条件下研究水泥环参数和套管缺陷对套管强度的影响。

1 计算模型及理论分析

1.1 计算模型及方法

根据之前学者的研究和大庆油田某井泥页岩的蠕变应力实验结果［20-22］，我们可以得出随着时间的推移水泥环所受的外挤力最终会趋近于地层的水平地应力，因此笔者认为不考虑地层的作用是相对合理的。本文假设水平地应力为均匀地应力，在这种情况下，建立了套管和水泥环在均匀外载条件下的三维有限元模型。利用Ansys 对建立的套管和水泥环有限元模型进行分析计算，模型的参数和边界条件如下：套管采用N80 套管，其屈服强度为758 MPa，内径为127 mm，外径为139 mm，高度为1500 mm，弹性模量为210 GPa，泊松比为0.3；水泥环的参数是随着模拟的不同而变化的；在水泥环的两端施加固定约束，外压均匀作用在水泥环外表面，套管和水泥环之间不考虑相对滑动，接触形式设置为粘接。

因为套管的长度大约为套管直径的10.8 倍，远大于2 倍，因此可以忽略套管边缘的边界效应；为了判断套管是否存在长度效应，因此需要求解判断套管类型的临界长度，公式如下［23］：

式中：D——套管的外径，mm；t——套管的壁厚，mm。

当套管的长度大于套管的临界长度时，为长套管；小于临界长度时，为短套管。套管模型的临界长度等于783 mm，模型的长度远大于套管的临界长度，因此不用考虑短套管对套管强度的增强效应。套管是典型的不具有SD 效应的材料，因此可以用Von Mises 等效应力来表示套管的应力状态。假如在加载过程中，套管应力达到屈服极限，不考虑套管屈服后力学特性的变化［24］；套管的外径与套管的壁厚之比约等于23.2，大于20，因此可以把套管看成薄壁管，理论上可以不考虑套管内压对套管应力分布的影响。

根据API 套管强度计算公式，可以看出套管有4 种破坏形式——屈服破坏、塑性破坏、弹塑性过渡破坏和弹性破坏。除了套管的屈服破坏外，其余3种破坏形式均可称为失稳破坏。实际上，除了一部分小直径大壁厚套管外，套管多发生失稳破坏，而不是屈服破坏，套管发生失稳破坏的临界压力小于套管屈服破坏发生的临界压力。套管模型的径厚比为23.2，大于套管发生屈服破坏的临界径厚比13.38，所以套管发生失稳破坏，其临界失稳破坏压力等于32.4 MPa（考虑到API 套管强度公式的安全系数为1.3～1.5）。因此，为防止套管发生失稳破坏，使套管处于弹性范围内，要控制水平均匀地应力σH＜50 MPa。

套管在由于加工生产的缺陷，导致其有一定的偏心率和椭圆度，套管的缺陷会改变套管上的应力分布，在套管缺陷地方出现应力集中，导致套管屈服破坏，这将会降低套管的抗外挤强度。Issa J.A.等［25］得出了套管偏心率和椭圆度对套管抗外挤强度的影响的公式。

模型基本假设：（1）套管除了偏心率或者椭圆度并无其他缺陷，且只考虑了偏心率和椭圆度单独作用的结果；（2）不考虑温度变化对套管强度的影响；（3）套管变形类型——弹塑性变形。图1 展示了椭圆偏心套管的简化模型。

图1 偏心套管和椭圆套管的简化模型Fig.1 Simplified model of eccentric and elliptical casing

1.2 偏心套管的理论分析

通过研究偏心率e从0 到0.5 范围内对破坏强度的影响，得出偏心率强度减小函数。然后使用非线性回归分析将关系与简单多项式拟合。该多项式的形式为：

式中：e——套管的偏心率；δ——偏心距，mm；t——套管壁厚，mm。

尽管偏心率强度减小函数是基于偏心率从0～0.5 得出来的，但当偏心率e=1 时，套管的抗外挤强度为0。这和物理实际是相对应的，即当其内径接近其外径时，管的抗挤压性接近零。说明了该公式在套管偏心率0.5～1 的范围内也有一定的准确度。公式的自变量仅有套管偏心率一个，因此套管强度修正系数仅受套管壁厚和偏心距的影响，与套管长度和外压力无关。

套管强度修正系数是指椭圆套管或者偏心套管在相同外压下，理想不射孔套管的内表面等效应力与缺陷套管内表面等效应力的比值，它反映了套管的偏心率或椭圆度对套管抗压强度的影响。图2为套管强度修正系数与套管偏心率之间的关系。

由图2 可得，套管的偏心率对套管的强度有很大的影响。随着套管偏心率的不断增加，套管的强度修正系数不断减小，也就是套管的强度逐渐降低。当偏心率为0.5 时，套管的强度降低仅为原来的40%。

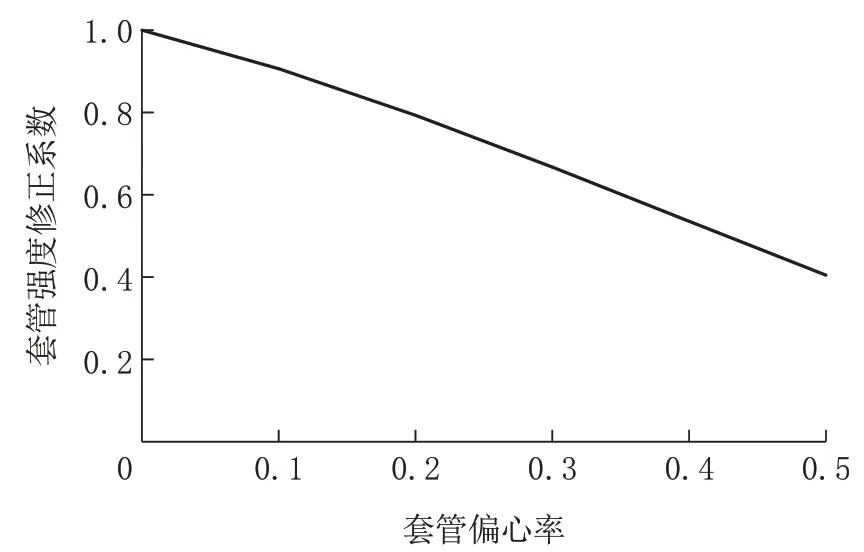
图2 套管强度修正系数与套管偏心率之间的关系Fig.2 Relationship between casing strength correction factor and casing eccentri city

1.3 椭圆套管的理论分析

套管椭圆度对套管强度的影响公式是通过在API 5CT 规范允许的椭圆度比范围内构建一系列模型得出的。其适用于套管椭圆度在0～0.002 之间，但经过实验验证，该公式在套管椭圆度小于0.1时均有较高的准确度。

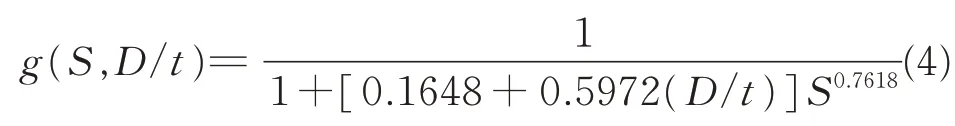
式中：S——椭圆度；D/t——套管径厚比，无量纲。

外径为129 mm、壁厚为6 mm 的套管，即径厚比为23.17 的套管的套管强度修正系数和套管椭圆度的关系如图3 所示。

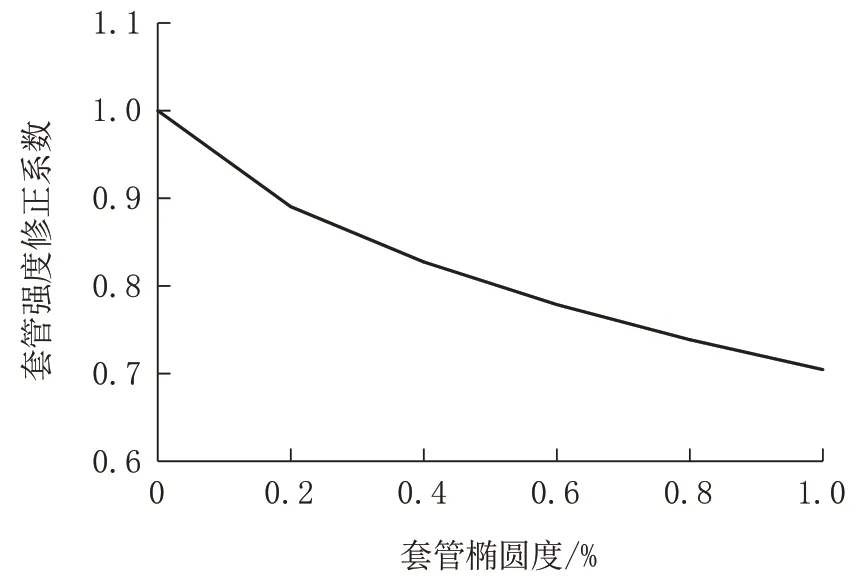
图3 套管强度修正系数和套管椭圆度之间的关系Fig.3 Relationship between casing strength correction factor and casing ovality

由图3 可知，套管的强度修正系数随套管椭圆度的增加而减小。套管的椭圆度对套管的强度影响比较大，当套管椭圆度等于1%时，套管的强度仅有套管原有强度的70%左右。

2 水泥环对套管抗挤强度的影响

2.1 水泥环弹性模量对套管抗挤强度的影响

通过控制变量法分析水泥环弹性模量对套管抗挤强度的影响，因此要保持水泥环的厚度不发生变化。研究结果表明，当荷载均匀分布时，减小水泥环厚度使之在10～20 mm 范围内能有效提高套管抗挤强度［26］。所以本文取水泥环的厚度为10 mm，泊松比等于0.15，水泥环的弹性模量依次为0、5、10、20、30、40、50 GPa（0 GPa 即无水泥环条件），均匀地应力的变化范围为10～50 MPa。根据图4可以得出以下几条结论：第一点是套管内表面等效应力随水泥环弹性模量增加的变化趋势不是简单的正比反比关系，而是先增加后减小，在5 GPa 时达到峰值。当水泥环弹性模量为50 GPa 时，水泥环会使套管内表面的应力下降大约13%；但是当水泥环弹性模量比较小时，水泥环的存在还会增大套管内表面的等效应力。当水泥环弹性模量Ec在20 GPa左右时，有水泥环套管内表面等效应力与无水泥环套管的等效应力大致相等。因此，在进行固井设计时，要保证水泥环的弹性模量超过此临界值（20 GPa）。第二点是通过与陈占锋等［15］计算结果比较，不难发现这个临界值会随套管径厚比的变化而变化。第三点是水平均匀地应力越大，套管内表面等效应力大小受水泥环弹性模量的影响越大，即在均匀地应力水平高的时候，套管内表面应力随水泥环弹性模量的增加降低幅度大，但其变化趋势不受地应力大小的影响。

图4 不同地应力条件下水泥环弹性模量对套管抗挤强度的影响Fig.4 The effect of elastic modulus of cement sheath on the strength of casing under different in‑situ stress conditions

2.2 水泥环厚度对套管抗挤强度的影响

水泥环的弹性模量不能无限制的增加，因此仅仅依靠提高水泥环的弹性模量来改善套管的受力状态是不合理和不现实的。所以要从另一个角度出发，研究水泥环厚度和套管内表面应力大小之间的关系。但在不改变套管直径的情况下，增加水泥环厚度就意味着要增加井眼直径，实现起来比较困难，且成本比较高，因此，可通过合理设计井身结构来解决此问题。为了更好地研究水泥环厚度对套管抗挤强度的影响，取水泥环的厚度范围为5～30 mm，弹性模量取 5、10、20、30、40 和 50 GPa，均匀水平地应力为40 MPa，以套管内表面应力大小作为衡量指标。

图5 显示了水泥环厚度和弹性模量与套管强度之间的关系，从图中可以看出，当水泥环的弹性模量＜20 GPa 时，随着水泥环厚度的增加，套管内表面的应力会逐渐增加，且增加的幅度受水泥环弹性模量影响；当水泥环弹性模量为5 GPa、厚度为15 mm 时，套管内表面等效应力增加了10%；当水泥环的弹性模量处于20～50 GPa 之间时，套管内表面等效应力随水泥环厚度的增加而减小，且其减小幅度随水泥环弹性模量的增加而增加。由此可见，增加水泥环的厚度不一定能改善套管的受力状态，只有在水泥环弹性模量＞20 GPa 时，增加水泥环厚度才能减小套管内表面等效应力。这印证了水泥环弹性模量对套管强度影响得出的结论。这个结论与人们的认知存在一定的出入。

图5 水泥环厚度对套管强度的影响Fig.5 The effect of cement sheath thickness on casing strength

发生上述现象的原因如下：水泥环的弹性模量比较小，即水泥环抵抗弹性变形的能力比较弱，也就是说，在水平均匀地应力下，水泥环很容易发生弹性变形，又由于在有限元分析中，一般会假设水泥环是线弹性材料，且水泥环不发生脆性破裂，在这种情况下，水泥环就像一个刚度系数比较小的弹簧，会有一个反力作用在套管上，同时远场原位地应力的大小是不发生变化的，因此，套管上的外载荷就等于地应力和水泥环反力的和，因此引起套管内表面等效应力的增加。当水泥环弹性模量比较大时，水泥环抵抗弹性变形的能力强，在地应力作用下，水泥环自身可保持自身的形状和稳定性，因此，水泥环传递给套管的力小于地应力，所以增加水泥环的弹性模量和厚度可改善套管的受力状态。对于套管内表面应力在水泥环弹性模量为5 GPa 时达到峰值这个问题，是因为当水泥环弹性模量＜5 GPa 时，水泥环的反力和弹性模量成正比，当水泥环弹性模量为5 GPa 时，水泥环初具自身的稳定性，这种稳定性会降低水泥环的反力，进而降低水泥环和套管之间的作用力。

因此在进行固井设计时，要考虑水泥环厚度、水泥环弹性模量的耦合作用结果，且要保证水泥环的弹性模量大于临界弹性模量。最优方案是同时增加水泥环的厚度和弹性模量［21］。

2.3 水泥环的存在对套管强度的影响

根据上述模拟结果可知，如果水泥环的厚度和弹性模量是一个适当的组合，水泥环可大幅度提高套管的承载能力。Evans G. W.等［16］、林元华等［27］通过实验室实验得出了水泥环可提高套管强度20%～30%，但都是在某种特定型号套管和特定水泥环条件下得出的，并没有研究水泥环对不同径厚比套管强度的影响。本文将对此问题做出分析。假设水泥环的厚度等于20 mm，弹性模量等于30 GPa，泊松比等于0.15，套管的外径等于139 mm，通过改变套管的内径来改变套管的径厚比，套管内径的变化范围为127～135 mm，套管外压力变化范围为10～50 MPa。

根据模拟计算得出的套管水泥环应力云图（见图6～7）。可以看出，套管内壁是整个套管上等效应力最大的地方，即最容易发生破坏的地方。套管强度增强百分比等于无水泥环套管内表面等效应力减去有水泥环套管内表面等效应力，再除以无水泥环套管内表面的等效应力。根据图8 可以看出，套管的强度增加百分比与套管的径厚比成正相关，即随着套管径厚比的增加，含水泥环套管的强度增加比较大。当套管的径厚比为11.6 时，含水泥环套管的强度仅增加了5%～6%；而当套管的径厚比等于34.8 时，套管强度增加了30%左右。并且，水泥环对套管强度的增强效果不受地应力大小的影响。因此，我们可以得出只有在套管径厚比比较大时，水泥环才能大幅度提高套管的强度。

图6 含水泥环和不含水泥环套管的等效应力分布图Fig.6 Equivalent stress distribution of casing with and without cement sheath

图7 含水泥环和不含水泥环套管的位移分布图Fig.7 Displacement distribution of casing with and without cement sheath

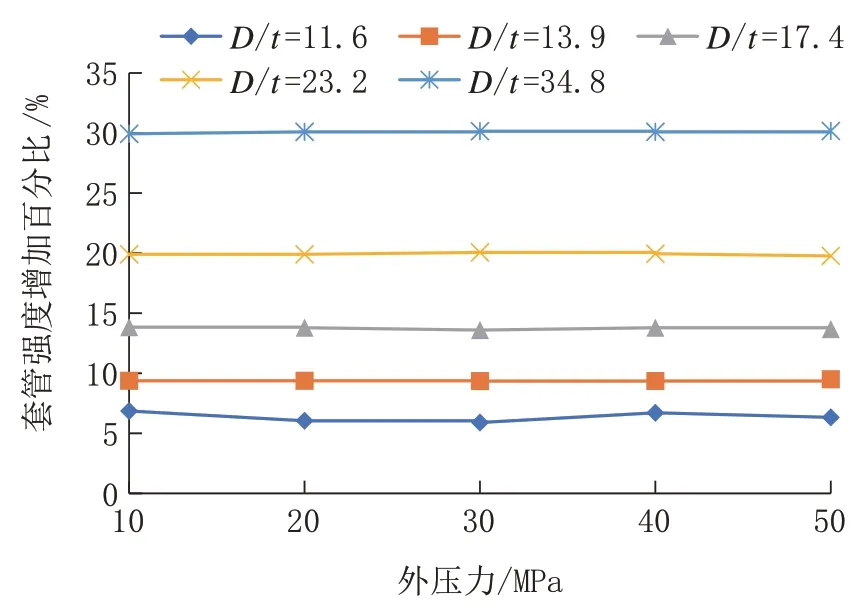
图8 水泥环对不同径厚比套管的强度影响Fig.8 The effect of cement sheath on the strength of casing with different diameter to thickness ratio

3 偏心率和椭圆率对套管强度的影响

3.1 套管偏心率对套管强度的影响

建立了含水泥环和无水泥环偏心套管的有限元模型，模型参数及边界条件如下：套管外径139 mm，壁厚6 mm，高度1500 mm，水泥环厚度为10 mm，弹性模量为30 GPa。在套管或水泥环的两端施加固定约束，外力作用在套管或水泥环外表面，大小为30 MPa。

套管内表面应力云图如图9 所示，套管的偏心使套管内表面在壁厚比较小的部位出现了应力集中，其应力集中程度随偏心率的增加而增加。对于无水泥环偏心套管，当偏心率为0.5 时，套管的强度降为原来的53%，与理论计算结果相差了10%左右，考虑到模型参数、边界条件等问题，10%的误差是可以接受的。同时表明了建立的有限元模型是比较合理的。根据图10 可得出：（1）无论是有水泥环套管还是无水泥环套管，套管的强度均会随套管偏心率的增加而大幅度减小，两者之间的关系接近于线性；（2）对于有水泥环套管，水泥环的存在可降低套管偏心率对套管强度的影响；（3）水泥环对偏心套管强度的影响是套管偏心率的函数，随着套管偏心率的增加，水泥环的作用效果越明显。

图9 偏心套管应力云图Fig.9 Stress nephogram of eccentric casing

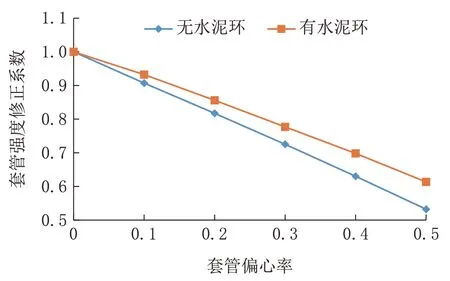
图10 套管强度修正系数和套管偏心率之间的关系Fig.10 Relationship between casing strength correction factor and casing eccentricity

3.2 套管椭圆度对套管强度的影响

建立了椭圆套管的有限元模型，模型参数与偏心套管相同。通过改变套管的椭圆度，分析套管内表面应力和椭圆度之间的关系。

根据椭圆套管内表面的应力云图（图11）可清晰看出，在椭圆套管长轴方向上出现了应力集中，套管的长轴方向与套管壁厚比较大的方向一致。椭圆套管内表面的变形云图显示（图12），套管内表面变形最大的地方在套管的短轴方向上。并且随着椭圆度的增加，套管的变形也是在不断地增加，极大地降低了套管的抗外挤强度。对于无水泥环椭圆套管，当椭圆度为1%时，套管的强度降为原来的62%，与理论计算结果相差了8%左右。同时表明了建立的有限元模型是比较合理的。根据图13可得出：（1）无论是有水泥环套管还是无水泥环套管，套管的强度均会随套管椭圆度的增加而大幅度减小；（2）对于有水泥环套管，水泥环的存在可大幅度降低套管椭圆度对套管强度的影响，即水泥环可以提高椭圆套管的强度；（3）水泥环对椭圆套管强度的影响随套管椭圆度的增加而增强，当套管椭圆度为1%时，水泥环使套管的强度提高11%。

图11 椭圆度为1%时套管内表面应力云图Fig.11 Stress nephogram of casing inner surface when ellipticity is 1%

图12 椭圆度为1%时套管内表面位移云图Fig.12 Cloud diagram of displacement of inner surface of casing when ovality is 1%

综上所述，套管的强度会随着套管偏心率和椭圆度的增加而减小，并且套管椭圆度对套管强度影响比较大；水泥环的存在会提高偏心套管和椭圆套管的强度，且对于椭圆套管，水泥环提高套管强度的作用更加明显。

图13 套管强度修正系数和套管椭圆度之间的关系Fig.13 Relationship between casing strength correction factor and casing ovality

4 结论

通过对上述Ansys 有限元模拟结果分析，并与陈占锋等［15］、张睿栋等［17］模拟结果的对比，可以发现，模拟结果基本上是吻合的，因此可以得出模拟参数的选取是比较合理的，对固井参数的选取具有指导意义。合理的固井参数可以大幅度延长套管的使用寿命，对增加油田的经济效益和稳产增产有重大意义。

（1）建立了理想套管、偏心套管和椭圆套管含水泥环和不含水泥环的有限元模型，并利用Ansys有限元分析软件进行了分析求解。主要研究有水泥环参数、套管偏心率和椭圆度对套管强度的影响。

（2）水泥环厚度不变条件下，只有当水泥环的弹性模量大于一定值，增加水泥环的弹性模量和厚度才能提高套管的承载能力；因此，在固井设计时，水泥环的弹性模量要大于此值。

（3）水泥环的存在不一定会增加套管的强度，只有水泥环的弹性模量大于一定值时，水泥环才能改善套管的应力状态，并且水泥环对套管强度的增幅效果是套管径厚比的函数。

（4）套管的强度和套管的偏心率、椭圆度之间的关系为负相关；与偏心套管相比，套管强度随套管椭圆度的增加减小得比较明显，且水泥环对椭圆套管强度的增幅更加明显。对套管加工误差提出了新的要求，并为套管加工参数的确定提供了一定的理论依据。