化归思想在高中函数中的简单应用

杨金诺

(黑龙江省伊春市第一中学 153000)

一、化归思想概述

函数问题侧重于解决实际问题，化归思想讲究的也就是实际运用.在学习的过程中，知识点是有限的，但是题型是无限的，不同于以往的“问题—解决—新问题—解决”的解题思路，化归思想讲究的是“知识点—问题—新问题—知识点”的解决方式.用已知的定义新的知识，并解决新的问题，就是化归思想的核心.在解题过程中，可以运用多种方式和方法，进而实现解题的目的.

二、化归思想的意义

化归思想可以归为唯物主义的观点之一，在唯物主义中，将抽象的物体具体化，复杂的问题简单化，化整为零是其核心思想之一.化归思想在解题的时候强调转化，众所周知，任何数学思想都是在解题和学习的过程中不断总结和归纳出来的，在解题过程中我们追求的是速度和准确率，而化归思想可以很好地满足该条件.

高中数学学习中，函数是十分重要的学习对象之一，高中的函数包括三角函数、对数函数、反比例函数等八种函数.我们解题时会发现基本的函数会演变成各种各样的形式，比如复合函数、复数函数或者是抽象函数等，如何运用基本的函数形式来解决这类比较复杂的函数就显得十分重要.此时就可以考虑利用化归思想，将函数转化为基本函数的形式，利用函数的性质和特点，或者是图象等方式解决问题.

三、化归思想在函数中的应用

化归思想在函数解题中十分常见，为了更好地了解其在解题过程中的重要性，我们可以通过具体的例题进行分析.

1.已知推算未知

在解函数题过程中，我们常常会遇见陌生的函数题型，化归思想的基础就是将未知的问题转为已知的问题.比如我们在解三角函数相关的问题时，可以考虑将其转化为二次函数等简单的函数，利用二次函数的性质进行求解.这样就可以将复杂抽象的问题简单化、具体化.不仅可以很好地解决问题，还可以加深对已学知识的理解和运用.例如在学习三角函数时，最常见的就是证明题.

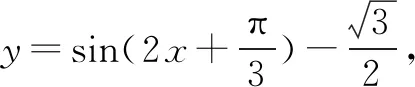
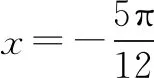
2.数形结合的方法

数形结合的方法也是我们解题时最常用的方法.因为数字是抽象的符号，但是数据过多的时候，我们就很难理清楚各个数据之间的关系,过多的数据会导致我们忽略一些数据，而在解题过程中，任何一个数据都有着很大的意义.通过数形结合，一方面可以使得抽象的问题具体化，另一方面可以使得数据的获取更加全面.

数字与图形自古就有，很多时候可以互相转化.函数的一个特点就是抽象，虽然它能解决具体问题，但是解决过程却十分抽象.为了更好地掌握函数，通过数形结合方法将代数问题转化成几何问题，显得更加生动和直观.

例2关于x的方程2x2-3x-2k=0在(-1, 1)内有一个实根，则k的取值范围是什么？

该题目是求k的取值范围，但是题干中的方程中还含有一个变量x，我们可以通过转化2x2-3x-2k=0，使其变成函数y=2x2-3x，这样一来，我们就将题目变成求解y=2x2-3x和函数y=2k的交点个数问题.

图1

在解这一类题目过程中，如果采用单纯的解题方式，很容易造成漏解的情况，但是在采用数形结合的方法后，就显得一目了然.

3.复杂变量简单化

在解函数题的过程中，当涉及到过多变量的情况时，题目就会显得十分繁琐，通过化归思想中变量转化的方法，将复杂的变量简单化可以让我们更好地理解题意，降低错误率.

例3若cos2θ+2msinθ-2m-2<0恒成立，试求实数m的取值范围.

该题目是求m的取值范围，但是题干的条件中除了m之外，还有sinθ和cosθ两个函数，这样一来，在这个题目中一共有三个变量，而我们掌握的是二元函数，所以考虑将题目中的函数转化为二元函数.

通过转化变量的方法，令sinθ=t，则cos2θ=1-sin2x，于是f(t)=t2-2mt+2m+1.

根据题目的要求，只要满足f(t)>0在[-1，1]上恒成立即可求实数m的取值范围.

解析令sinθ=t，可以得出，要想cos2θ+2msinθ-2m-2<0恒成立，可以通过转化变量，设f(t)=t2-2mt+2m+1，则只要f(t)>0在[-1，1]上恒成立.

由于f(t)=(t-m)2+2m+1-m2(-1≤t≤1)，所以只要f(t)的最小值大于零即可.

若m<-1，则当t=-1时，f(t)min=2+4m，令2+4m>0，得m>-0.5，这与m<-1矛盾，故舍去；

若m>1，则当t=1时，f(t)min=2，所以m>1.

这个题目原本十分复杂，但是在转化成二次函数之后，题干部分就显得十分简单明了，这样就可以很好地降低解题的难度.

4.正面问题反面化

正面的问题反面化也就相当于运用了矛盾的思维.在解数学题时，经常会遇见题干十分简单，但是却无从下手的情况；或者是采用常规的解题方式十分麻烦，而且很难达到我们想要的结果.为了更好地解决问题，我们可以采用化归思想中的反向思考的方式，也就是我们常说的逆向思维.

例4已知函数f(x)满足：f2(x)-2f(x)f(x+1)+2f(x+1)=0(x∈R)，证明：f(x)不可能为正比例函数.

根据题目的要求，我们要证明f(x)不可能为正比例函数，首先就是利用化归思想，将该函数和正比例函数的相关性质关联起来，然后利用函数转化的思想，将其转化为一般的函数.假设f(x)=kx(k≠0),代入f2(x)-2f(x)f(x+1)+2f(x+1)=0,得-kx2+(2k-2k2)x+2k=0对任意x恒成立，故必有k=0，但由题设知k≠0，所以假设不成立.所以f(x)不可能为正比例函数.

在解题时，我们的思维一定不能局限于课堂上的知识或者是已知的知识，更重要的是融会贯通，这样才可以更好地解决问题.

5.隐藏条件明显化

函数解题的过程中，很多条件都是隐藏存在的，针对这一类情况，我们可以通过知识之间的联系融会贯通，充分利用这些条件，达到解题的目的.

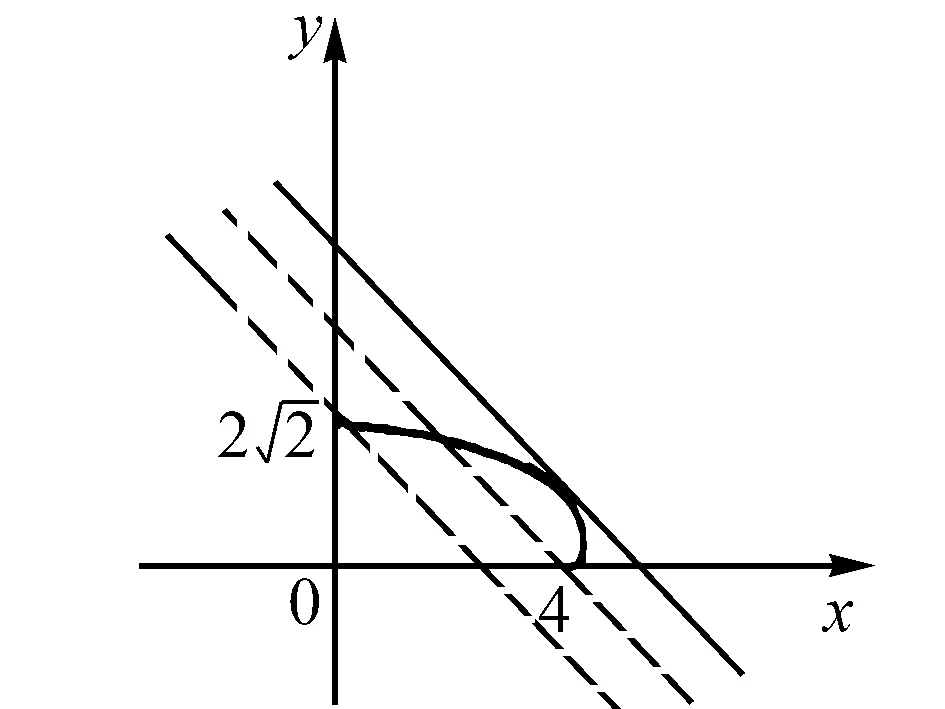
图2

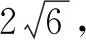
化归思想在很多时候和数学中的转化思想十分相近，但是又不完全一样，它侧重的是一种归纳，是对已学和已知的知识的归纳.这样在遇见新的问题或者是复杂的问题时，也可以很好地解决.要想很好地掌握这种数学思想，最基础的就是多练习、多思考，才可以很好地运用化规思想.