基于改进扰动观察法的光伏系统MPPT研究
郭昆丽,闫 东,付建哲
(西安工程大学电子信息学院新能源研究所,陕西 西安 710600)
光伏发电因其资源丰富且对环境友好受到广泛的关注,然而光伏电池属于非线性装置,受到光照强度、温度等外界环境的影响,输出功率时刻都在发生改变[1]。为了在一定的限定条件下提高光伏电池对能量的转换效率,降低光伏发电产品的制造成本,使得光伏阵列输出最大功率,就需要运用一些算法对其进行跟踪[2]。当前的主要算法有扰动观察法、模糊控制法、粒子群算法等,但是每种算法都有优缺点,需要选择合适的方法用于最大功率追踪(MPPT)[3-7]。
文献[8]提出一种自适应扰动观察法用于最大功率追踪,对于光伏电池输出功率的变化,不断调整电压扰动值,追踪花费时间少,到达稳态时震荡小,动态性能和稳态性能优越,但是采样过程增加了低通滤波器,系统工作较为复杂。文献[9]将扰动观察法和电导增量法结合追踪最大功率,追踪最大功率花费时间短,但其两级步长的选取应相匹配,否则难以保证稳态性能。文献[10]将恒定电压法和变步长电导增量法相结合的算法用于MPPT,追踪速度快,但是稳态震荡大。
针对以上问题本文提出一种将恒定电压法、扰动观察法、电导增量法三种算法相结合的改进算法用于最大功率追踪,避免了恒定电压法容易受到外界环境的影响难以追踪到最大功率的缺点,同时又兼具扰动观察法易于实现,电导增量法稳态震荡较小的特点,有效解决扰动观察法跟踪速度和稳态精度之间的矛盾,降低了光伏发电产品的成本。
1 传统扰动观察法
如图1所示,光照强度一定时,温度越低光伏电池输出功率越大,温度一定时,光照强度越强,输出功率越大,且每条P-U曲线都有一个最大功率点和与之相对应的电压。
扰动观察法具体流程如图2。
如图2所示,U(k)、I(k)、P(k)为当前时刻检测的光伏电池电压、电流、功率,U(k-1)、I(k-1)、P(k-1)为上一时刻检测的光伏电池电压、电流、功率。

图1 光伏电池输出特性曲线
这种控制方法结构简单易于实现:步长过大,扰动次数减小,需要花费的时间少,但是稳态震荡较大,能量损耗过大;步长过小,需要扰动次数增大,花费时间多,但是到达稳态震荡较小,能量损耗小。此外,如果外界环境变化大,可能造成一定情况的误动,难以追踪到最大功率。
2 改进扰动观察法
针对以上传统方法表现出来追踪速度和稳态精度所存在的矛盾,本文将恒定电压法、扰动观察法、电导增量法三种方法相结合,用于最大功率追踪。

图2 定步长扰动观察法流程图
由P-U曲线可知,最大功率点左侧斜率为正,随着光伏电池输出电压的增加,斜率逐渐减小,到达最大功率点时斜率为零;最大功率点右侧斜率为负,且随着光伏电池输出电压减小,斜率逐渐减小,到达最大功率点时斜率为零。基于此,改进算法先用恒定电压法使得光伏电池输出功率靠近最大功率点,再对爬坡的斜率进行判断,采用大步长ΔU1进一步靠近最大功率点,最后采用小步长ΔU2追踪到最大功率,这样既缩短了追踪时间,又减小了到达最大功率点时的震荡,具体流程如图3所示。

图3 改进扰动观察法流程图
3 仿真结果分析
3.1 仿真分析
为验证本文所提算法的可行性和有效性,在MATLAB/Simulink中搭建仿真,参数设置为开路电压Uoc=43.3 V,短路电流Isc=10.84 A,最大功率点电压Um=39 V,最大功率点电流Im=10.35 A,温度为25 ℃,光照强度S=1 000 W/m2,a=1×10-2W,b=3×10-3W。
采用算法一进行仿真,结果如图4所示;采用算法二进行仿真,结果如图5所示;采用算法三进行仿真,扰动观察法步长ΔU1=2×10-3V,ΔU2=2×10-4V,结果如图6所示。对仿真结果进行数据统计,如表1所示。

图4 算法一仿真结果图

图5 算法二仿真结果图
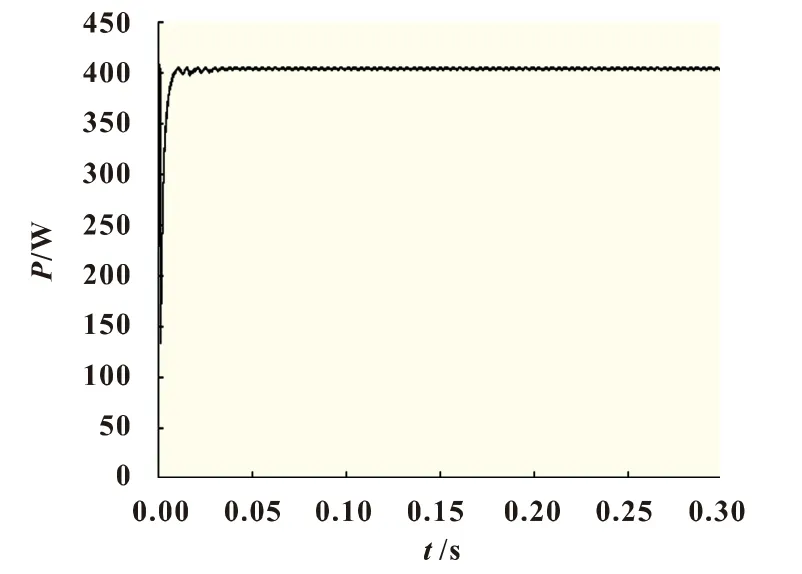
图6 算法三仿真结果图

表1 3种算法下的仿真结果
从表1可以看出,算法二比算法一到达稳态时间少,追踪速度快,且稳态震荡减小了56.74%;算法三到达稳态的时间接近算法一的一半,但稳态震荡率减小了90.72%;改进算法三到达稳态时间比算法二减小了32.35%,但稳态震荡率减小了78.54%。由此可知,算法三不仅缩短了最大功率追踪的时间,而且也降低了稳态震荡的幅度,解决了追踪速度和稳态精度之间的矛盾,具有良好的追踪效果。
3.2 验证改进算法的跟踪情况
为了验证当环境改变时,改进算法能否快速适应环境的改变,追踪到最大功率,仿真结果如图7所示。图7(a)是温度为25℃不变,光照强度S从1 000 W/m2开始,在0.1 s时降低为700 W/m2,在0.2 s时升为900 W/m2,可以看出追踪效果良好,到达稳态时震荡较小;图7(b)是光照强度S为1 000 W/m2不变,温度从25℃在0.1 s时升为35℃,在0.2 s时降为30℃,可以看出由于温度变化量有限,功率波动并不明显。从图7可以看出当光照强度改变或温度改变时,改进算法仍然具有良好的追踪效果。
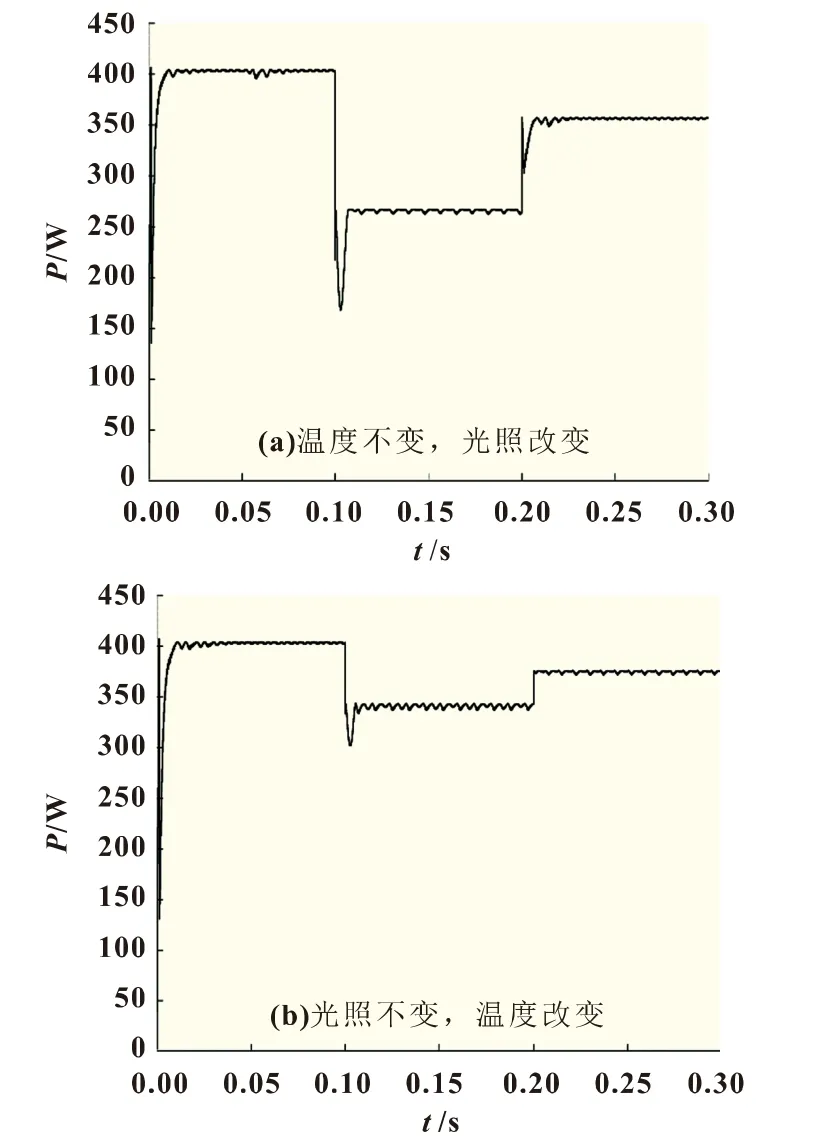
图7 仿真结果
4 实验验证
为进一步验证改进算法的有效性,搭建实验平台,IGBT采用SKM300GB12T4,二极管使用DH2χ61-18A,光伏阵列模拟器使用E4350B,实验平台使用DSP+FPGA结构,其中DSP芯片使用TMS320F28335型号,示波器为TEK-TPS2024型号,光伏阵列模拟器参数设置为Uoc=61.4 V,Isc=10.23 A,Um=49.1 V,Im=8.31 A,温度为25℃,光照强度S为1 000 W/m2。

图8 实验结果
图8中,通道1为光伏阵列输出的电压波形,通道2为光伏阵列输出的电流波形,通道3为光伏阵列输出的功率波形。从图8(a)可以看到改进算法的启动时间为0.48 s,速度较快,从图8(b)可以看出光照从1 000 W/m2降低为600 W/m2,改进算法追踪到最大功率点用时0.24 s,具有良好的动态性能,且稳态震荡率为0.47%,稳态性能较好。
5 结论
针对传统扰动观察法步长大,花费时间短,稳态震荡大和步长小,花费时间长,稳态震荡小的问题,本文在传统扰动观察法的基础上进行改进,进行了仿真和实验验证,得出以下结论:
(1)改进后的扰动观察法一方面能够缩短最大功率追踪的时间,另一方面降低了到达稳态时震荡的幅度,减小了能量的损失,具有良好的追踪效果。
(2)温度不变,光照强度的改变对于最大功率具有明显影响:光照增加,光伏阵列输出功率明显增加;光照减小,输出功率明显减小;光照强度不变,温度改变,功率变化不大。

