比例谐振算法和扰动观测器控制的单相逆变器

陈红兵， 闵晶妍

(营口理工学院电气工程学院，辽宁 营口 115014)

电压型逆变器是可再生能源并网的重要接口，随着可再生能源接入比例的增加，当前电力系统将越来越依赖逆变器。考虑逆变器的可靠性，逆变器应具备在孤岛情况下为负载提供电能的能力，这对逆变器输出电压的质量提出了更高的要求。在逆变器的控制方法中，电压/电流双环控制得到了广泛应用，采用此控制方法，将逆变器控制成了一个带内阻抗的非理想电压源，输出电压随负载电流的变化而波动。为了抑制逆变器输出电压的波动，最直接的方法是提高逆变器控制系统的环路增益，但是提高环路增益会破坏逆变器控制系统的稳定性，导致逆变器的输出特性不尽如人意[1]。

为了避免因提高环路增益导致系统失稳的问题，采取了如下措施：第一，使用电流传感器检测负载电流，再进行前馈补偿是一种简单可行的方法。在实际工程中，多采用比例前馈补偿的方式，此方法削弱了低频电流对输出电压的影响，但是对于中高频谐波电流的抑制效果并不明显。采用比例微分前馈方式虽然在理论上可以抑制全频域内负载电流的影响[2]，但是前馈环节引入的附加阻抗特性必须匹配逆变器的输出阻抗特性，才能消除负载电流对输出电压的影响。使用传感器采集负载电流进行前馈补偿的方式不仅增加了传感器、信号传输和处理电路等成本，还占用了处理器的AD接口，其准确度也受传感器和信号处理电路精度的影响[3]。第二，在双闭环控制参数整定过程中，一般忽略负荷和直流母线电压的扰动，为了简单，一般忽略掉滤波电感的寄生电阻，且等效电感为恒定值。但是，在实际系统中，滤波电感的寄生电阻不但存在，而且会随着电流的变化而变化。

为了提高逆变器输出电压的动态和稳态性能，本文采用了一种易于实现的方法，也就是基于扰动观测器的扰动前馈控制策略，并且将负载电流、直流电压变化和电感变化设为外部扰动量，建立了逆变器的扰动观测模型，通过扰动观测器(DOB)观测扰动量[3]，再将观测量前馈至电流环的比较处，提高输出电压对负载电流、直流电压变化和电感变化的抗扰动能力，改善逆变器的输出特性。分析表明，与传统双环控制相比，本文所提出的控制策略可以使被控对象标称化，对逆变器参数摄备较强的鲁棒性。

1 单相逆变器的数学模型及控制框图

单相逆变器的主电路如图1所示，L和C分别为交流侧滤波电感和滤波电容，r为电感的寄生电阻，R为负载，uab(t)为桥臂侧电压，udc为直流侧电压。因此，单相逆变器的数学模型为：

式中：d(t)为占空比；il(t)为电感电流；iL(t)为负载电流；uc(t)为电容电压。

图1 单相逆变器的主电路

为了抑制负载变化、电感寄生电阻变化、电容变化和直流电压波动等扰动，提出了采用扰动观测器(DOB)观测它们，然后将它们前馈到电流比较点，用来补偿这些扰动。因此，单相逆变器的控制方法如图2所示。

图2 单相逆变器的控制方法

图2所示的双闭环控制框图，外环为负载电压控制环，控制其交流电压，由于电压是50 Hz的交流量，PI控制器不能实现无静差控制，因此，引入了比例-谐振(PR)控制算法实现无静差控制[4-5]，即：

式中：kp,u和kr,u分别为PR控制算法的比例系数和谐振系数；ωc为带宽频率，ω0为谐振频率，在本文中ωc取7 rad/s，ω0取2 π×50 rad/s。

控制方案的内环为电流环，其被控制量也是交流量(电流)，但是设置内环的主要任务是改造控制对象，提高系统的稳定性，本文拟采用PI控制算法，即：

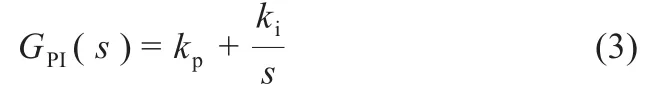
式中：kp和ki分别是PI控制算法的比例系数和积分系数。

2 控制算法参数的整定

2.1 电流环控制算法参数的整定

电流环控制算法的设计应保证系统的稳定性及快速响应能力，由图2可知，电流环的开环传递函数为：

电流开环传递函数的固有极点s=－r/L在原点附近，这将导致在低频处电流环的开环增益和相位开始下降，从而增大了电流环的稳态误差，于是通过设置零点s=－ki/kp抵消此电流环的极点[5]，即令：

此时电流环的闭环传递函数为：

式中：τi为电流闭环传递函数的时间常数，τi=L/kp，由式(4)和(5)可得电流控制算法的参数：

由式(7)可知，电流环控制算法的参数取决于时间常数τi，为了提高电流环的快速性，τi应设置得较小；并应保证电流环的带宽1/τi远小于逆变器的开关频率(一般小于1/10的开关频率)[5]。

2.2 扰动观测器(DOB)的分析与设计

从图2可知，负载电流作用在控制系统的前向通道上，当它变化时，影响输出电压的大小，因此是典型扰动。直流电压udc也在前向通道上，当它变化时，也会影响输出电压的大小，并且通过等效变换，可以认为它是作用在负载电流点的扰动。在图2中，电感和电容分别在负载电流的左右两侧，当它们变化时，通过等效变换，可以将这些变化变换到负载电流扰动处，它们也是扰动。因此，可以将负载电流、直流电压波动、电感寄生电阻的变化和电容的变化一并看成单相逆变器控制系统的扰动[3]。

首先，用扰动观测器(DOB)观测负载电流、电感变化、滤波电容变化以及直流电压的波动情况，然后再将这些扰动量前馈到电流指令比较点处，抑制这些扰动。电压控制环及扰动观测器结构图如图3所示[6]。

图3 嵌入扰动观测器后，电压环控制框图

图3中，δ(s)为外部扰动，包括负载电流、电感变化、滤波电容变化及直流电压波动等；uc(s)为逆变器输出电压；P(s)为电压环的等效控制模型；Pn(s)为电压环的标称模型；Pn－1(s)为标称模型的逆；Q(s)为滤波器；ξ(s)为测量噪声；Gu(s)为电压控制算法。根据图3，未投入DOB时，逆变器输出电压uc(s)的表达式为：

由式(8)可知，电压指令uref(s)与系统外部扰动δ(s)共同决定了逆变器的输出电压uc(s)的值，δ(s)将影响uref(s)的控制误差。

投入DOB之后，逆变器输出电压的表达式为[7-8]：

由式(13)可知，若Q(s)≈1，则外部扰动可以完全抑制，被控对象被控制为标称模型，但是存在逆变器控制系统对所测量噪声敏感的现象。由于等效扰动是低频扰动，而测量噪声是高频噪声，所以，从频率的角度考虑，希望Q(s)为低通滤波器。当频率小于截止频率时，被控制模型为标称模型，低频扰动可以被有效抑制；当信号频率高于截止频率时，|Q(jω)|≈0、|φξ(jω)|=0，高频噪声信号得以有效抑制[8-9]。由以上分析可知，Q(s)是设计扰动观测器的关键。

2.3 滤波器的设计

滤波器Q(s)的相对阶数和时间常数直接影响了DOB补偿扰动的能力和系统的稳定性。为了在物理上能够实现，Q(s)的阶数尽可能小，其相对阶数必须大于或等于等效被控对象Pn(s)的相对阶数[10-11]；时间常数决定了Q(s)的带宽，必须折衷考虑DOB的鲁棒性和补偿能力。

电流环校正之后，等效成一阶惯性环节，该惯性环节与电容传递函数结合，组成了一个二阶系统。根据2.2节及文献[8]的分析，低通滤波器可选用的形式为：

式中：τ1=0.001 5 s。

2.4 电压环控制算法的参数整定

整定电压环控制算法参数时，应实现电压指令的准确跟踪，同时保证电压环有足够的稳定裕度。电压环的开环传递函数为：

电压环的截止频率取ω=250 Hz，在截止频率处，电压环的相角裕度应大于45°，幅值裕度大于10 dB[12]，根据上述稳定裕度要求，先算出kp,u和kr,u的取值范围，再选择合理的值。

3 仿真实验

本文建立了MATLAB/Simulink仿真模型，对所提控制方案进行了仿真研究和验证，仿真参数见表1。

表1 绘制零极点所用参数

逆变器带非线性负载时，其输出电压如图4所示。逆变器输出电压的THD为4.28%，它的正弦度高，可见用所提控制方案控制的单相逆变器，能给非线性负载提供优质的电能。

图4 带非线性负载时，逆变器的输出电压

当直流侧电压波动(直流电压从800 V跳变到600 V)时，逆变器的输出电压如图5所示。在跳变的瞬间，逆变器的输出电压没有任何波动，可见扰动观测器几乎抑制了直流电压的跳变扰动。

当负载从3 kW跳变到4.5 kW时，逆变器输出电压如图6所示。图6(a)是常规方法控制的逆变器，它的输出电压突然降低了6 V，持续了大约一个周期(20 ms)。图6(b)是所提控制方法控制的逆变器，输出电压没波动，可见扰动观测器(DOB)抑制了负载电流的扰动，改善了逆变器输出电压的暂态性能和静态特性，有效抑制了因负载突变所带来的电压波动问题。

图5 当直流电压突变时，逆变器的输出电压

图6 当负载突变时，逆变器的输出电压

当电感的寄生电阻在0.2 s时刻从10 mΩ变化到20 mΩ时，逆变器的输出电压如图7所示。输出电压几乎没有变化，仅仅是电压的THD从0.14%变化到了0.15%。

4 结论

比例谐振控制器加扰动观测器控制方案大幅减小了逆变器输出电压的跟踪误差，在不同负载情况下，使逆变器的输出电压保持恒定，即使在非线性负载的情况下，输出电压质量也较高。它改善了逆变器输出电压的暂态性能，有效地抑制了负载突变所带来的电压波动问题，提升了输出电压波动的恢复速度，增强了逆变器控制系统的鲁棒性和稳定性。

图7 滤波电感的寄生电阻变化时，逆变器输出电压