基于有限元超载法的重力坝深层抗滑稳定分析

舒建国，程昌勇

(水利部珠江水利委员会技术咨询中心，广东 广州 510611)

1 重力坝深层抗滑稳定问题

重力坝发展至今，坝工技术日渐成熟，可满足一般设计要求。随着设计坝高不断增加，地基地质条件愈加复杂，随之产生的重力坝抗滑稳定安全问题愈加突出。当坝基内存在多个软弱结构面、夹层、节理时，会将坝基切割成不连续体，形成连续滑移路径，在水荷载及其他荷载作用下，坝体有可能连同部分基岩沿软弱滑动面滑移失稳，造成重力坝深层抗滑稳定问题。

重力坝深层滑动大致分为3种形式[1-2](如图1所示)：

图1 深层滑动模式示意

① 坝址下游由于长期流水冲刷作用，存在冲沟、冲坑等临空面，坝基岩体可能沿缓倾角软弱夹层向临空面方向滑移失稳；

② 坝址下游岩体为缓倾角软弱岩体，或存在横向软弱破碎带，在各荷载作用下易发生褶曲、压缩，甚至剪切破坏，导致坝基岩体沿软弱面滑动；

③ 沿坝基岩体中存在两条(或多条)缓倾角软弱结构面，分别倾向上游和下游，即本文要讨论的双斜滑动面滑移。

2 稳定分析方法的研究现状

2.1 刚体极限平衡法

目前对于深层抗滑稳定的分析方法和稳定安全系数的计算，我国规范规定以刚体极限平衡法计算为主，必要时可辅以有限元法、地质力学模型试验等方法并进行综合评定，其成果可作为坝基处理方案选择的依据，有关重力坝深层抗滑稳定的规定见《混凝土重力坝设计规范》(SL 319—2018)附录E[3]坝基深层抗滑稳定计算。

在水利坝工设计中，刚体极限平衡法应用十分普遍，其优点如下：

① 建模简单，计算方便，容易操作；

② 工程实践经验丰富，与之相配套的设计规范和安全系数标准也比较成熟。

但此方法只能对坝基的抗滑稳定进行整体分析，无法进一步了解其应力、应变，且无法对坝基的抗滑稳定安全度和破坏机理做出精确的分析。

2.2 弹塑性力学有限单元法

受刚体极限平衡法的局限性，为更加准确的分析该问题，提出更为合理的分析方法，即利用弹塑性力学有限单元法分析坝体及地基中的应力和应变，进而确定其深层抗滑稳定安全系数。此方法在重力坝深层抗滑稳定计算模型中考虑了软弱结构面及坝体、坝基的影响，将应力、应变、位移、失稳机理、最终安全度结合在一起，能较精确地计算出坝体和坝基内各单元节点的应力和变形[4-5]。

超载法属于弹塑性力学有限变形法的一种[6]，计算坝体抗滑稳定安全系数时要先施加实际荷载，得到正常运行状态下坝体、地基的应力、应变等，然后加大作用荷载，直至大坝失稳破坏，得到此时坝体及地基的应力、应变及超载安全系数，并据此判断大坝安全度。

超载法分为超水位法和超水重法，其本质是模拟作用荷载的不确定性以及评价坝体承受超载作用的能力。本文采用超水重法。

3 ABAQUS简介

ABAQUS是一款功能强大的有限元分析软件[7]，可解决实际工程中复杂模型的高度非线性问题。对于大多数数值模拟，只需提供结构的几何形状、材料性质、荷载情况、边界条件等工程数据即可进行分析计算。对于非线性问题的分析，ABAQUS能自动选择合适的收敛准则及荷载增量，在分析过程中对这些参数进行调整，保证结果的精确度。ABAQUS拥有丰富的单元库和材料模型库，可以用于模拟各种复杂的几何形状及大多数工程材料。ABAQUS强大的分析功能可解决水利工程涉及到的水压力、温度场、渗流场、重力场等问题，以及进行隧洞开挖、滑坡、结构抗震等模拟。

4 超载法计算基本原理及评判准则

超载法计算基本原理为假定岩体强度参数不变，然后逐级超载上游水荷载，坝体自重及其他荷载不超载，分析坝基变形破坏演变发展过程与超载倍数的关系，寻求坝基整体滑移时相应的超载倍数Kp，以此作为坝基整体抗滑稳定超载安全系数。

对重力坝进行深层抗滑稳定分析，需明确坝体如何才被认为失稳的问题，即稳定评判准则。

1)在超载法分析过程中，随着荷载的逐步加大，首先在局部小范围出现剪压或拉裂屈服区，随后这一屈服破坏范围逐步扩大，直到贯通，丧失保持稳定的能力，这时坝体发生失稳破坏。因此，可采用屈服区是否贯通来判断坝体、坝基的整体安全度。

2)在运用有限元分析软件计算时，若发生计算不收敛，则说明坝体、坝基发生较大变形，可作为判断坝基是否发生失稳破坏的准则。

5 算例

5.1 基本资料

本文针对双斜滑动面分析。算例模型中(如图2所示)，坝体坝高为130 m，顶宽为20 m，底宽为100 m。蓄水位为128 m，夹层厚为0.52 m。坝基内有2条软弱夹层AB和CD，其中AB倾向下游，倾角为13°；CD倾向上游，倾角为13.6°，交点C深度为56 m。

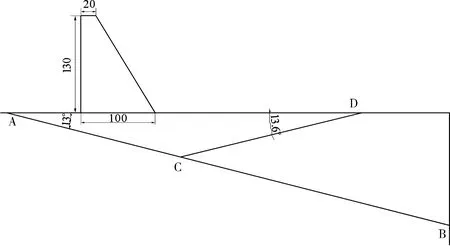
图2 算例示意

5.2 建立几何模型

模型如图3所示。

图3 模型示意

5.3 定义材料属性

本模型将坝体和地基定义为弹性材料；将软弱夹层定义为弹塑性材料，并采用Mohr-Coulomb屈服准则。

大坝和坝基的力学参数见表1。

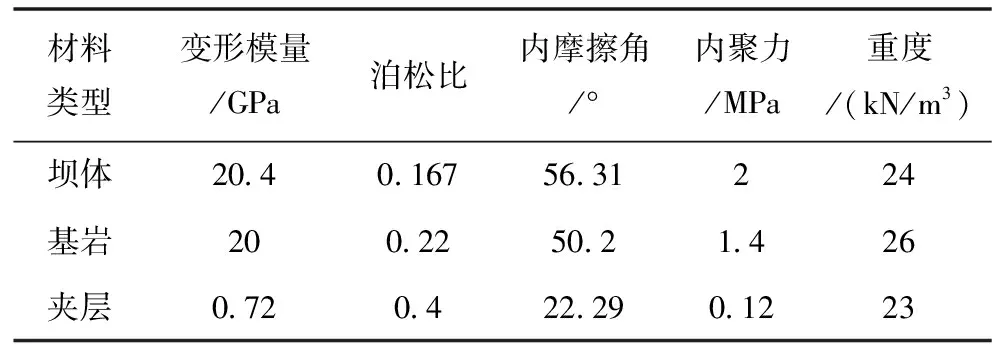
表1 坝体和坝基的力学参数

5.4 定义分析步

本模型定义3个分析步：Initial Step、Step-1、Step-2。

其中，Initial Step为ABAQUS/CAE自动创建。Step-1用来一次性加载重力；Step-2用来分步加载水荷载，加载步数在计算过程中由10步增加到50步。

Mohr-Coulomb模型需应用非对称算法，因此在Equation Solver Method区域中将Matrix storage设为Unsymmetric，即非对称分析。

5.5 模拟荷载及约束

在本次研究分析过程中，仅考虑重力与静水压力，按照蓄水位和公式p=γh可得静水压力，分布如图4。

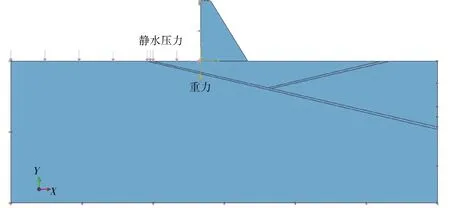
图4 荷载、约束示意

5.6 划分网格

模型坝体、基岩、夹层采用CPE4作为主要单元类型，少数部分采用CPE3。划分网格时，在重点区域加密网格单元，边界处采用较疏的网格单元。单元总数为7 458个(其中CPE4有7 266个，CPE3有192个)，节点总数为7 528个(如图5所示)。

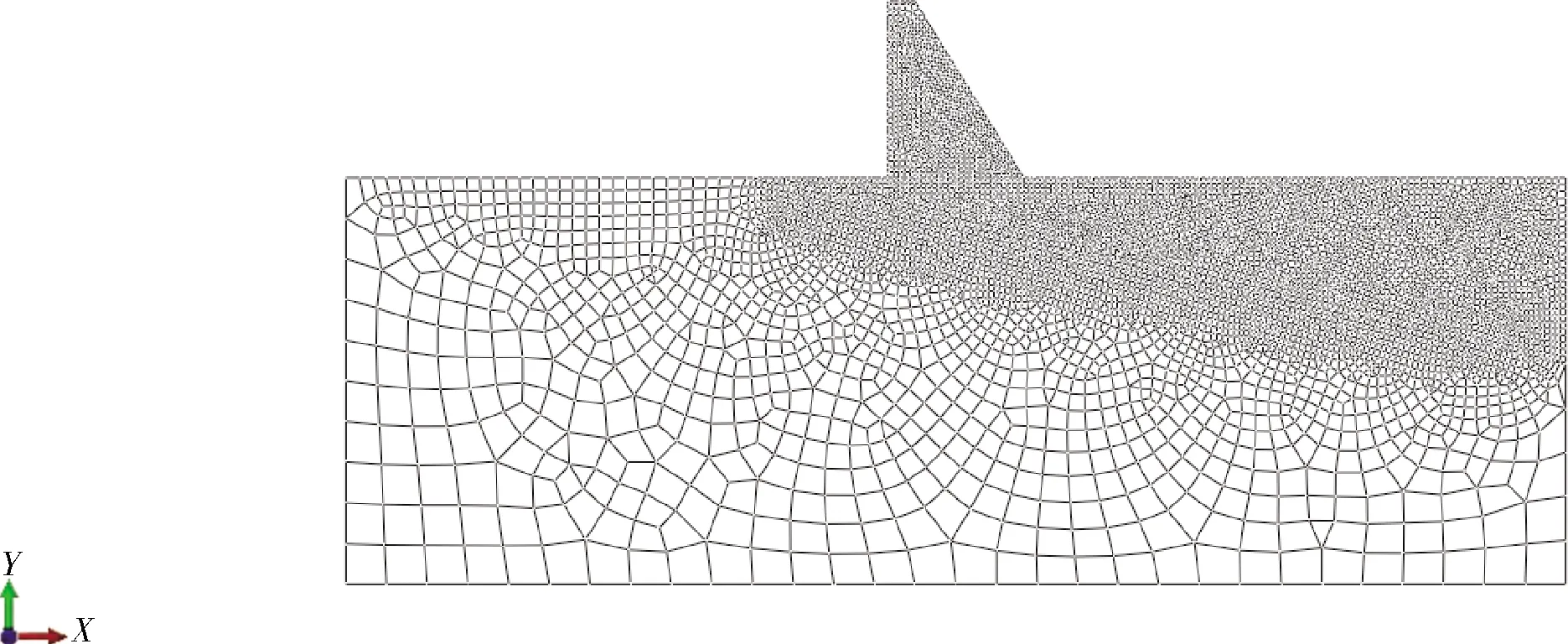
图5 单元网格示意

5.7 计算结果分析

为研究坝基随超载系数的增大而发生的渐进破坏过程，计算从正常运行状态(Kp=1)开始，逐步增大超载系数Kp(1.2，1.6，2.0，2.4，2.6，3.0，3.2，3.6，4.0，4.6)，直至出现计算不收敛。

导出其部分PEMAG(积分点等效塑性应变)示意、应力场示意、位移场示意(如图6～14所示)。

由图6～14可知，随着超载系数的增大，软弱夹层的塑性区范围不断扩大，当Kp=3时，软弱夹层AC已全部进入塑性，此时CD段尚未进入塑性，坝趾应力为1.08×107Pa，位移为0.094 m，坝踵应力为1.86×107Pa，位移为0.090 m；当Kp=3.6时，软弱夹层ACD已全部进入塑性，但尚未进入极限状态，坝趾应力为2.44×107Pa，位移为0.133 m，坝踵应力为1.39×107Pa，位移为0.131 m；当Kp=4.6时，坝趾应力为5.36×107Pa，位移为0.172 m，坝踵应力为3.05×107Pa，位移为0.170 m。坝踵屈服区的范围较大，坝踵区应力集中明显，坝踵区小范围内拉应力超过了容许拉应力值，且当系数继续提高，计算不收敛，说明此时软弱夹层达到极限状态；另外通过有限元计算，坝趾处的塑性区扩展方向及第三主应力扩展方向一般是倾向下游的，可以作为刚体极限平衡法中第二滑裂面的倾向[8]。

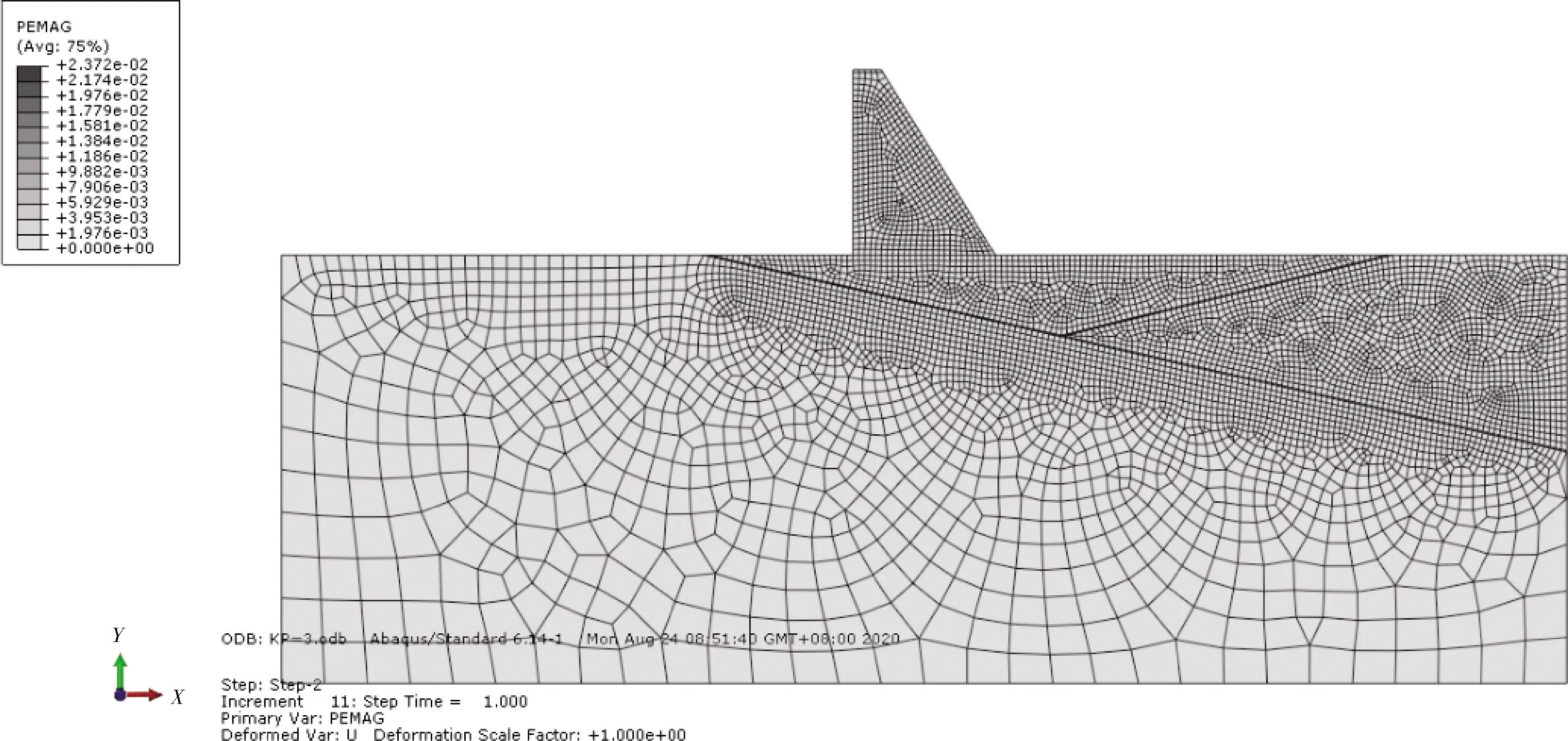
图6 Kp=3塑性应变示意

综上所述，根据不同的稳定安全判据得到超载系数(见表2)。

现在，我是厂长了，景花厂的厂长。就这么快。一人之下，众人之上。阿花是老板，在我的上面。偶尔也会在我的下面。在我下面的时候，她像只发情的母狗。

图7 Kp=3应力场示意

图8 Kp=3 位移场示意

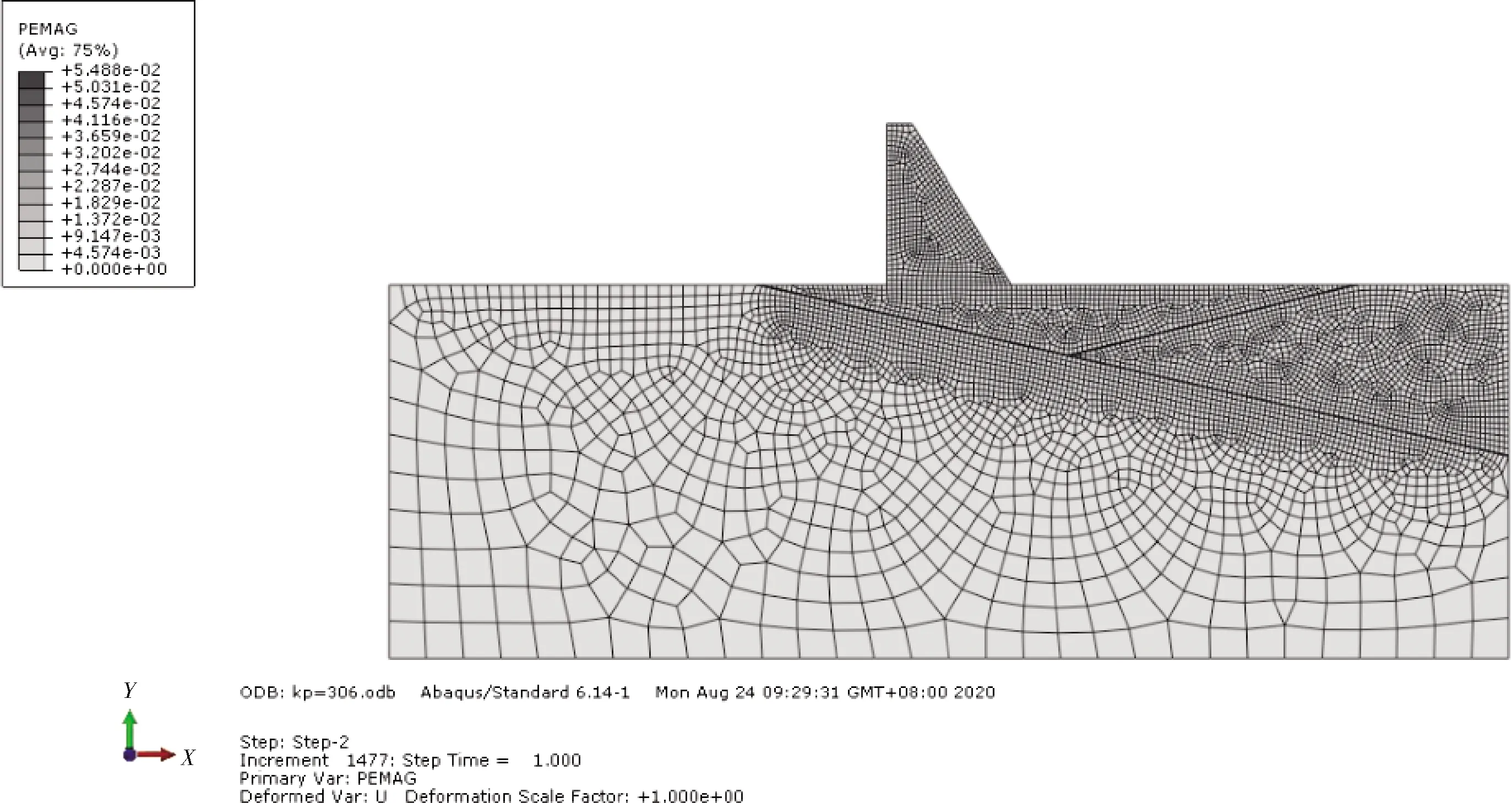
图9 Kp=3.6塑性应变示意

图10 Kp=3.6应力场示意

图11 Kp=3.6 位移场示意

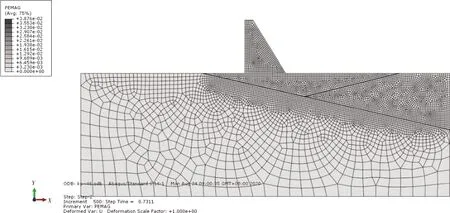
图12 Kp=4.6塑性应变示意

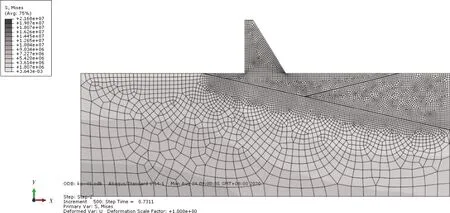
图13 Kp=4.6应力场示意

图14 Kp=4.6 位移场示意

表2 各判据对应的超载系数

由表2中数据可知，采用塑性区贯通比例所确定的抗滑稳定安全系数，相对用计算收敛准则确定的抗滑稳定安全系数偏于保守。

5.8 刚体极限平衡法

采用现行规范规定的刚体极限平衡法计算其抗滑稳定系数(如图15所示)。

图15 刚体极限平衡法计算双斜面滑动示意

1)被动抗力法

被动抗力法是令BCD块体处于极限平衡状态解出抗力Q后再以AB面为主滑面，计算ABD块体沿AB面的抗滑稳定安全系数K，并作为整个坝段的抗滑稳定安全系数，根据基本资料及式(1)：

(1)

式中Q为抗滑力，kN；G1、G2分别为岩体ABD、BCD重量的垂直作用力,kN；α、β分别为软弱夹层面AB、剪切破裂面BC面与水平面的夹角；f为AB软弱夹层面、BC剪切破裂面的抗剪断摩擦系数；c为AB软弱夹层面、BC剪切破裂面的抗剪断凝聚力,kPa；A1为AB面的面积,m2；φ为BD面上的作用力与水平面的夹角,夹角φ值需经论证后选用，从偏于安全考虑φ可取0。

由式(1)得Q=81 986.6 kN；将Q代入式(2)：

K1=

(2)

式中K1为按抗剪断强度计算的抗滑稳定安全系数;W为作用于坝体上全部荷载(不包括扬压力，下同)的垂直分值,kN;∑P为作用于坝体上全部荷载的水平分值,kN;U1、U2、U3分别为AB、BC、BD面上的扬压力,kN;Q为BD面上的作用力；其他符号意义同式(1)。

由式(2)得：以AB面为主滑面，抗滑稳定安全系数K=1.98。

2)剩余推力法

按块体静力传递原理，假设上游块体处于极限平衡状态，求解上下游两个滑块之间的剩余推力Q，考虑剩余推力的作用，再计算下游块体的安全系数。根据基本资料及式(3)。

Q=

(3)

式中 各符号意义同式(1)(2)。

由式(3)得Q=43 857.4 kN；将Q代入式(4)。

(4)

式中K2为按抗剪断强度计算的抗滑稳定安全系数，其余符号意义同式(1)(2)。

由式(4)得：经计算比较该断面，当下游岩体沿β=35°剪断滑裂时最危险，其计算成果见表3所示，抗滑稳定安全系数K=2.26。

表3 深层抗滑稳定计算结果

6 结语

1)通过采用ABAQUS有限元分析软件,对此双滑面重力坝深层抗滑稳定分析结果表明，从稳定安全判据准则来看，采用计算收敛准则确定的抗滑稳定系数最大，而采用塑性区贯通确定的抗滑稳定系数其次，刚体极限平衡法所得到的抗滑稳定安全系数(K=1.98～2.26)最小。计算表明，有限元超载法、刚体极限平衡法计算得出的安全系数是有差异的，随着实践经验的不断积累，基本形成初步共识：以刚体极限平衡法计算的安全系数为安全度的主要判据，同时将有限元计算的坝体、地基的应力、位移值、超载系数Kp等作为辅助判据，综合衡量坝的稳定安全度。

2)由于传统极限平衡法由于假定太多，且只能给出安全系数，存在不足，继续在条分法的框架下做出新的发展比较困难。随着数值计算方法的不断发展和成熟，有限元方法为边坡稳定性分析提供了新的思路。目前常用的分析方法为超载系数或强度储备系数，这两种方法均是通过使变形体对象处于破坏前的临界平衡状态获得其稳定安全度，是目前工程界应用最多的确定有限元安全系数的分析方法。重力坝的抗滑稳定性是坝工设计中重点关注的问题之一，现行规范规定的刚体极限平衡法计算只给出了单滑面和双滑面的计算公式，在实际应用时存在较大的局限性。当实际工程设计过程中遇到复杂地基情况时，可采用有限元计算方法研究其抗滑稳定性。