椭圆柱绕流的相关问题研究

张雪娇, 刘官厅

(内蒙古师范大学 数学科学学院,内蒙古 呼和浩特 010022)

绕流运动广泛存在于生活中,在水利、建筑和环境等实际工程中有很多应用,如风绕过飞机、火车和建筑物,水绕过船只、潜艇等。当流体绕过物体时,流体会对物体产生一定的力的作用,因此研究绕流运动具有很重要的实际意义[1-2]。文献 [3]对高层建筑周围的空气绕流运动做了数值模拟,文献 [4]分析了带阻流板海底管道管跨绕流流场,文献 [5]对有限平板绕流做了数值模拟。在目前绕流问题相关研究中,关于圆柱绕流的研究较多[6-10],文献 [11]总结了圆柱绕流的研究进展及展望,建议研究海洋工程中桩体、管线、立管的圆柱绕流问题。文献 [12]对圆柱绕流做了离散涡数值模拟,得到了多个圆柱不同情境下的流线图,文献 [13]研究圆柱绕流的大涡模拟。目前圆柱绕流的相关问题也已经具有相当成熟的结果,同时圆柱绕流也对许多其他绕流问题具有一定的指导意义和奠基作用。本文对椭圆柱绕流问题的研究就是以圆柱绕流问题为基础的,椭圆柱由于自身形状的优势,在对抗流体作用时有更大的优势,因此对椭圆柱绕流的研究具有重要的现实意义。

无粘性不可压缩流体的无旋运动是流体力学中的一种理想化模型,它是真实流体流动在一定条件下的简化,简化后许多问题可以得到很好地解决,故对它的研究意义重大。本文研究无粘性不可压缩流体的椭圆柱绕流运动,根据该流动的特点,利用复变方法求得复势函数,并且进一步求得势函数和流函数,画出流线图和等势线图。经过分析,与实际流动情况吻合较好。

1 问题陈述

图1 物理平面z

设长轴为2a,短轴为2b的无限长椭圆柱放置在无粘性不可压缩流体中,在无穷远处速度为V∞的均匀来流平行绕过该椭圆柱,冲角为α,流体做平面无旋运动。流动形式如图1所示。本文研究椭圆柱附近的流体流动情况以及椭圆柱体表面的压强分布情况。

2 基本方程

2.1 无粘性不可压缩流体无旋运动的速度势函数

无粘性不可压缩流体的无旋运动是流体力学中一种理想化的简单模型。无粘性不可压缩流体运动应满足连续性方程

divv=0

(1)

和运动方程[14]

(2)

其中v是流体速度,Fb是质量力,ρ是流体密度,p是流体压强。此外,对于不同的边界还应满足不同的边界条件。这组方程是非线性的而且速度和压强耦合在一起,求解比较困难。

如果在所讨论的流场区域中,流体运动是无旋的,即rotv=0,则一定存在一个势函数φ(x,y,z;t)使得v=φ。函数φ(x,y,z;t)称为速度势函数,将v=φ代入(1)式,则连续性方程变为

(3)

这是一个拉普拉斯方程,在给定的边界条件下可以求出它的解。对于正压流体和体力有势的情况,当流动无旋时,有拉格朗日积分

(4)

这样,无粘性不可压缩流体无旋运动的基本方程组变为

(5)

(6)

边界条件视具体边界而定。方程(5)是拉普拉斯方程,在数学上已有许多方法可求其通解。所以只需要求得φ,问题便迎刃而解。然而在边界比较复杂时,上述问题的求解仍有一定难度。

2.2 不可压缩流体平面运动的流函数

如果流体做平面运动,取此平面为x-y平面,则连续性方程[14]写为

(7)

这里vx,vy分别为流体速度v在x方向和y方向上的分量。引入一个新的标量函数ψ,使得

此时方程(7)自动满足。通常将标量函数ψ称为流函数。对于平面流动,流体涡量ω只有z轴方向上的分量,记为ω=ωk。从而有ω=-2ψk,又可以写为

ω=-2ψ,

(8)

在无旋运动的情况下,方程(8)化为

(9)

于是,对于本文所讨论的无粘性不可压缩流体的平面无旋运动,流函数ψ也满足拉普拉斯方程。只要找到流函数ψ,问题也可以得到解决。

2.3 平面无旋运动的复势

无粘性不可压缩流体的平面无旋运动可以引进速度势φ或流函数ψ来解决,它们都满足拉普拉斯方程。根据定义,在直角坐标系中[14]有

(10)

这说明这两个调和函数满足柯西-黎曼条件,因此它们可以组成一个解析函数

W(z)=φ(x,y)+iψ(x,y),

(11)

2.4 流场中的速度及压强分布

流场中的任意一点处的流体速度

(12)

对于流场中的任意一点处的压强p可以由伯努利方程求出

(13)

其中V∞、p∞和ρ∞分别为无穷远来流的速度、压强和密度。定义压强系数[14]

(14)

以描述流场中的压强分布。

3 椭圆柱绕流问题的解析解

3.1 基本思想

若C*为半径为R的圆周,则在平面ζ上复势函数为[14]

(15)

W*(ζ)=W*(F-1(z))=W(z)。

(16)

图2 数学平面ζ

3.2 保角变换

对于图1所示的问题,利用儒可夫斯基变换

(17)

其逆变换为

(18)

它将z平面上长轴为2a,短轴为2b的椭圆变换为ζ平面上半径为c的圆周(c=a+b),将椭圆外部区域变换为圆周外部区域,如图2所示。

3.3 势函数和流函数的计算

(19)

这与文献[15]的结果一致。

分离W(z)的实部和虚部得

(20)

其中

其中θ是x2-y2-a2+b2+i 2xy≐X+iY的辐角且k=0或1。

于是由(20)式可得

(21)

(22)

且当θ和k取不同值时,φ(x,y)和ψ(x,y)也不尽相同。对于势函数和流函数,由φ(x,y)=const可以画出等势线图。同理,令ψ(x,y)=const可以画出流线图,从而可以分析流体的流动规律。

3.4 压强系数

求得势函数和流函数后,由(10)式、(12)式、(13)式和(14)式可以得到压强系数cp(将在随后数值实例中讨论),进而可以画出压强系数图,以此来分析流场的压强分布。

4 数值算例

4.1 势函数和流函数

(23)

(24)

其中θ是x2-y2-3+i 2xy≐X+iY的辐角,且k=0,1。根据θ的不同取值可以将z平面(除去椭圆内部)划分为如图3所示区域。为了保证两个平面的绕流一一对应,需要对k的取值进行讨论,在区域1、区域2和区域6处取k=0,在区域3、区域4和区域5处取k=1。

(25)

(26)

同理,可以得到其他几个区域的势函数和流函数。

4.2 流线图

根据(25)式,令ψ(x,y)=const,并使const取适当的值,可以画出椭圆柱附件的流线图,如图4所示。

图3 六个不同区域 图4 区域1的流线图

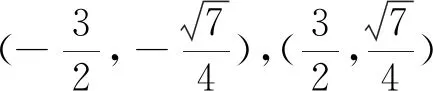
4.3 压强系数

根据在区域5和区域6的势函数,再利用(12)式、(13)式和(14)式可得区域5和区域6中椭圆柱表面的压强系数为

(27)

图5 区域5-6的压强系数图

压强系数图如图5所示。由图5可知,在x=-1.5处,压强系数达到最大值1,表明此处压强也达到最大值2 000+p∞,且流体速度v=0 m/s。在约x=-0.12处,压强系数cp=0,故此处压强p=p∞,速度v=V∞=2 m/s。

类似地,可以得到其他区域的椭圆柱表面的压强系数图,进而可以分析压强分布情况,此处不再赘述。

5 几种重要且特殊的情形

5.1 流动冲角为0的情形

当α=0时,流动复势函数(20)式变为

(28)

其中X1和Y1如上所述。仍采用实例5中的数值,于是当α=0时区域1的势函数和流函数分别为

(29)

(30)

同理,可以得到其他几个区域的势函数和流函数。

利用相同的方法,可以得到α=0时的流线图和等势线图,如图6和图7所示。

图6 α=0时的流线图 图7 α=0时的等势线图

图6中在(-2,0)和(2,0)处流线垂直于椭圆柱面,所以此处流体速度为0 m/s,这两点是驻点。在(0,-1)和(0,1)处流线最密集,故此处流体速度最快。从图7可以看出椭圆柱体表面的等势线垂直于柱体表面,远离椭圆柱表面的等势线逐渐变竖直,等势线与流线互相垂直,这与文献 [16]的结论一致。

类似地,可以画出区域5和区域6中椭圆柱面的压强系数图和区域1下半椭圆面的压强系数图,如图8和图9所示。

由图8可知,在x=0处,压强系数达到最小值,故此处压强最小,流速最快,符合流动情况。由图9可知,在x=2处,压强系数达到最大值1,故此处压强达到最大值2 000+p∞,且流体速度最小为v=0 m/s,这均与流线图所反映的情况一致。

5.2 退化为平板绕流情形

当椭圆柱短轴长退化为0时,该椭圆柱退化成长为2a的平板。此时问题变成平板绕流,保角变换[14](17)式退化为

(31)

其逆变换

(32)

将长为2a的平板变换为半径为a的圆周。复势函数化为

(33)

这与文献 [14]中的结果一致。

图8 区域5-6椭圆面的压强系数图 图9 区域1下半椭圆面的压强系数图 Fig.8 Pressure coefficient diagram for lower half ellipse in area 1 Fig.9 Pressure coefficient diagram for the the ellipse in area 5-6

分离W(z)的实部和虚部得到平板绕流的势函数和流函数分别为

(34)

(35)

其中,β是x2-y2-a2+i 2xy的辐角,k=0,1。

图10 六个不同区域

(36)

(37)

类似地,可以得到平板下平面的压强系数图(图13)。

图11 平板绕流流线图 图12 平板绕流等势线图

图13 平板下平面的压强系数图

6 结论

本文利用儒可夫斯基变换研究了无粘性不可压缩流体的椭圆柱绕流问题。结果表明,流体在流场驻点处的速度为0 m/s,压强在此处达到最大。压强系数用于描述压强分布时比较方便,且压强系数图所得结果可以很好地与流线图反映的结果呼应。从流线图、等势线图和压强系数图可以看出,椭圆柱绕流情况与实际流动情况吻合较好。当椭圆柱的尺度参数取特殊值时退化为经典的平板绕流情形。