基于PLSA 学习概率分布语义信息的多标签分类算法

王一宾 ,郑伟杰 ,程玉胜* ,曹天成

（1.安庆师范大学计算机与信息学院，安庆，246133；2.安徽省高校智能感知与计算重点实验室，安庆师范大学，安庆，246133）

大数据时代，文本数据分类［1］是当前的研究热点，因文本数据中含有多个主题，所以语义信息［2］的挖掘是主要研究的问题.多标签文本数据具有丰富的语义空间，语义空间的挖掘大多数应用在标签空间.在多标签算法中，特征与标签之间的联系与应用是近几年研究的热点，研究者们通过将标签对应几组特征、特征间与标签间的相关性信息等方法挖掘标签空间中语义信息，进而提升算法的性能.

大多数多标签数据具有维数较高的特征与标签空间，如何获取空间中的内在信息是面临的主要问题.针对这一问题，Huang et al［3］提出将特征与标签空间缩小到低维空间，从低维的特征空间获取潜在标签空间中的信息.标签嵌入［4］同样是获取标签空间中的内在信息主要方法，Kumar et al［5］提出将特征与标签分组对应投影到低维空间，标签向量嵌入到低维空间可保证各个组的稀疏性不变.特征间与标签间的相关性信息是特征与标签空间中的主要信息，许多研究者提出较好的学习方法.Cheng et al［6］利用均值漂移聚类［7］方法获得特征空间中的隐藏信息，并利用信息熵度量标签的相关性，采用一种非平衡化标签补全的方法重塑标签空间.但上述研究中，研究者们未能将特征与标签可能存在的先验分布信息用于提升算法的性能.Zhang and Wu［8］提出类属属性的多标签算法（Multi-label Learning with Label-Specific Features，LIFT），讲述不同标签可能存在自身的一些特征.

关于类属属性的多标签算法研究，利用标签间相关性信息度量标签的类属属性是常用方法.Huang et al［9］提出假设特征与标签相关联，相似的标签可以共享特征，标签间相关性用余弦相似度度量，但未考虑特征间的相关性信息.对于这一问题，Han et al［10］应用概率邻域计算图模型与余弦相似度分别计算特征与标签的相关性，进而度量标签的类属属性.在标签对应一组特征中，每个特征所占的比例可能不同.针对这一问题，MLFC（Multi-label Learning with Label-specific Features by Resolving Label Correlations）［11］算法提出对于每个特征分配权重，并同时构造其他特征用于学习标签间的相关性.上述方法是基于每个标签与小部分的特征相关联，这种稀疏性的假设在某些应用中并不能成立.因此，Weng et al［12］提出将数字标签转化为逻辑标签以丰富标签空间的语义信息，进而提升类属属性的多标签算法性能.上述对于类属属性的多标签算法改进中，仅在度量相关性方法与改造特征与标签空间上解决问题，未能学习特征与标签间可能存在的联系中潜在的语义信息.标签与实例是否同样可能存在一种联系，是值得思考与研究的问题.

在分析潜在语义信息的方法中，我们发现概率潜在语义分析（Probabilistic Latent Semantic Analysis，PLSA）［13］模型可以适用于多标签算法.PLSA 模型中文本与单词分别对应多标签算法中的实例与特征，最主要的是隐含变量主题对应标签.我们认为多标签数据中的标签隐藏在样本矩阵中，即样本矩阵中几个特征可能组成某个标签类似于PLSA 模型中几个单词可能组成某个主题.图1 展示了本文的主要思想.例如在关于旅行的文章中，像风景、美食与居民等这种词汇出现频率较高.对于旅行这个标签，可以看作是风景、美食与居民等这些特征的一种概率分布.在多标签文本数据集中，关于旅行的文章可能有日记的标签，而日记这个标签可以看作是时间与感想等特征的一种概率分布.总之，每个标签都代表一个不同的特征的概率分布，而每个实例又可以看作标签上的概率分布.多标签模型中的多个标签可以为PLSA 模型提供更多隐含变量，进而挖掘到丰富的语义信息.PLSA 模型可以为多标签模型中的特征与标签提供一种概率模型，并且每个变量以及相应的概率分布和条件概率分布都有明确的数学解释.

图1 PLSA 的多标签模型Fig.1 Multi-label model of PLSA

基于此，本文提出基于PLSA 学习概率分布语义信息的新型多标签学习算法.首先，在样本矩阵中进行无监督学习获取特征-标签与标签-实例的条件概率分布矩阵.其次，将获取到的两个矩阵放入算法框架中，训练学习概率分布语义信息.因在挖掘概率分布语义信息时未能获取隐含变量标签对应的奇异值，所以在模型设计中添加损失函数来影响优化模型的损失值.最后，在13个公开的多标签文本类型的数据集上进行实验和统计假设检验，并在其他类型多标签数据集上进行对比实验.结果表明，多标签算法学习概率分布信息可以提升算法的性能.

1 PLSA-ML 模型

1.1 多标签模型下的概率潜在语义模型本节把概率潜在语义分析模型引入多标签模型，表1列出了本文的常用符号及含义.

隐含变量为多标签模型中的标签向量yl，如同概率潜在语义分析模型中的多个单词可能组成几组主题，本文认为多个特征可能组成几组标签.对于实例与特征的联合分布为：

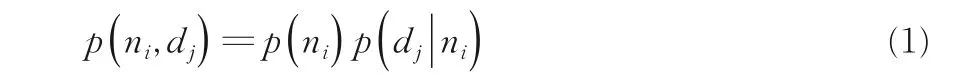
其中，ni与dj分别表示第i个实例与第j个特征.为了计算p(dj|ni)，引入隐含标签变量yl，有：

表1 常用符号Table 1 Notations frequently used

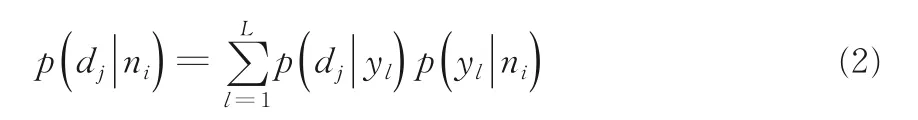
其中，yl表示每个标签.为了计算p(dj|yl)与p(yl|ni) 引入EM（Expectation-Maximization）算法［14］对两组参数进行估计.首先，针对本文提出的模型给出似然函数：

其中，t(ni，dj)表示特征dj出现在ni的次数.本文的E-Step 直接使用贝叶斯公式计算隐含变量yk在当前参数取值条件下的后验概率，有：

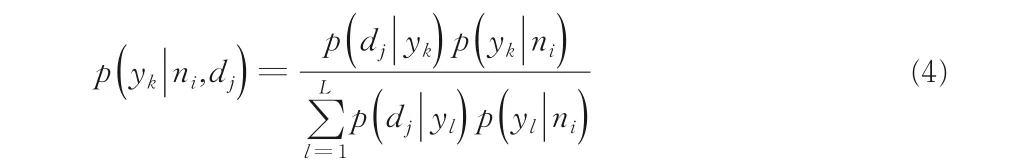
假设所有的p(dj|yk)与p(yk|ni)都是已知的，后面迭代的过程中取前M-Step 中的参数值.在M-Step 中最大化对数似然函数的期望，有：

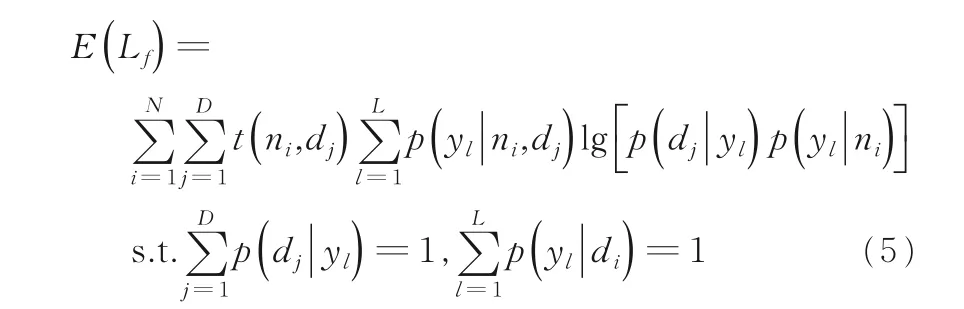
p(yl|ni，dj)是已知的，取值是前面E-Step 中的估计值.下面进行M-Step，发现这是一个多元函数求极值的问题，可以采用拉格朗日乘数法，得到的参数值迭代公式为：

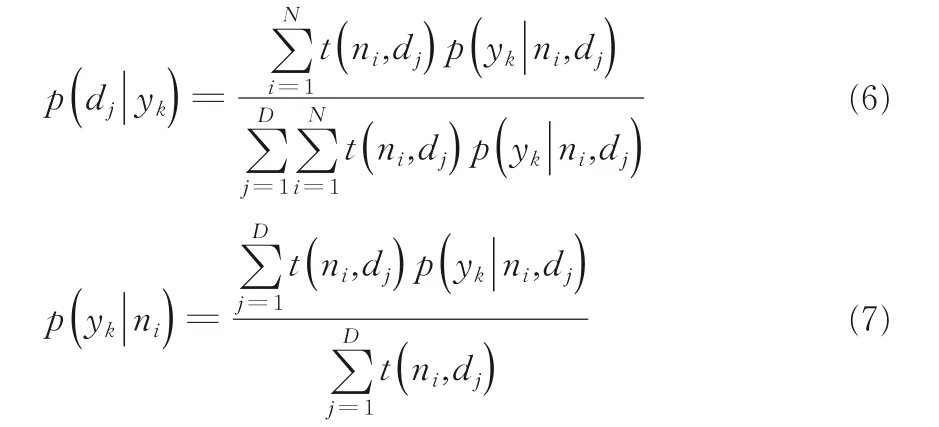
获得两种语义矩阵：Pd|y∈RD×L与Py|n∈RL×N，矩阵Pd|y是由每个p(di|yl)所组成；同样，矩阵Py|n是由每个p(yl|ni)组成.把矩阵Pd|y与Py|n放入多标签算法模型中，获取特征-标签与标签-实例间的条件概率语义信息.本文提及的语义信息指它们之间的条件概率值.

1.2 模型的建立多标签学习［15］中有输入训练数据X和标签矩阵Y，X∈RN×D，Y∈RN×L.S={(xi，yi) |1≤i≤n}是多标签一个训练数据集，xi={xi1，xi2，…，xid}是一个特征向量，yi={yi1，yi2，…，yil} 是一个标签向量，多标签学习任务是找到一个映射关系f：X→2Y.一般的多标签算法模型为：

其中，L(⋅) 是损失函数，α是正则化参数，W∈RD×L为权重矩阵.加入矩阵Pd|y与Py|n代表上述两种概率语义矩阵.由于构造模型前未计算标签奇异值，所以增加奇异值分解的损失项.交叉验证实验中每次得到标签奇异值是不同的.利用矩阵Py|n可以获取标签-实例之间概率语义信息.同样，矩阵Pd|y获取特征-标签之间概率语义信息.因此，得到本文提出的多标签算法模型：

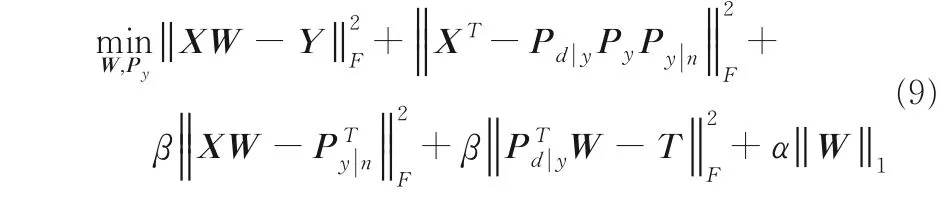
模型第一项是在训练集上预测多标签的损失项.第二项是对训练矩阵奇异值分解的损失项，上述已得到矩阵Pd|y与Py|n，需计算对角线为标签奇异值的对角矩阵Py.第三项将样本矩阵X投影到标签-实例概率语义空间中获取它们之间可能的联系.第四项将已获得的概率语义矩阵Pd|y投影到带有标签相关性的空间，目的是依据标签间相关性获取特征-标签概率语义信息.其中，参数β是控制学习语义信息的损失.矩阵T∈Rl×l是计算标签间余弦相似度矩阵C∈Rl×l的拉普拉斯矩阵，在学习语义信息时应考虑标签间的相关性.第五项是用l1-范数对权重矩阵W进行稀疏化，并防止算法产生过拟合，参数α控制权重矩阵的稀疏性.PLSA-ML 具体操作流程如图2 所示.

图2 PLSA-ML 模型Fig.2 PLSA-ML model

1.3 模型的优化本节给出模型优化过程，用交替迭代计算模型中两个变量矩阵W与Py.在求解过程中，由于带有l1-范数变量W的模型是非平滑的，不能直接求导进行求解，所以根据加速梯度下降方法［16］并参照Liu et al［17］求解变量W.

首先，计算权重矩阵W，目标函数为：

由于l1-范数的正则项是非平滑的，故目标函数（式（10））是非平滑的，为此使用近端梯度下降法解决目标函数非平滑的问题，目标函数变为：

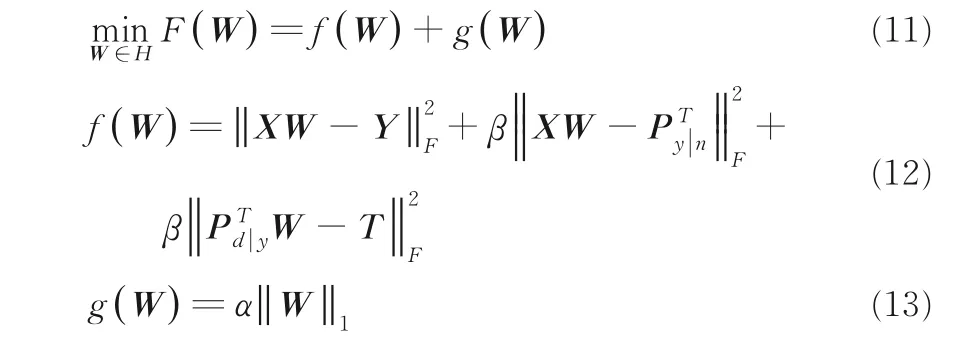
其中，H是希尔伯特空间，f(W)是凸函数，f(W)满足Lipschitz 条件，即对任意矩阵W1，W2，有：

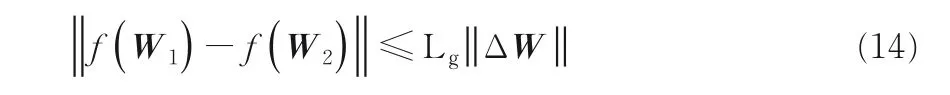
其中，Lg是Lipschitz常数，ΔW=W1-W2.加速梯度下降过程中不能直接最小化F(W)，需引入Q(W，W(t))二次近似F(W)，因此定义Q(W，W(t))：

其中，序列bt满足可以提高收敛到O(t-2)的速度，因此Wt可以当作W第t次迭代的结果.每次的迭代需要通过以下软阈值函数：

下面计算Lipschitz 常数，对于给定W1与W2，根据f(W)满足Lipschitz 条件：

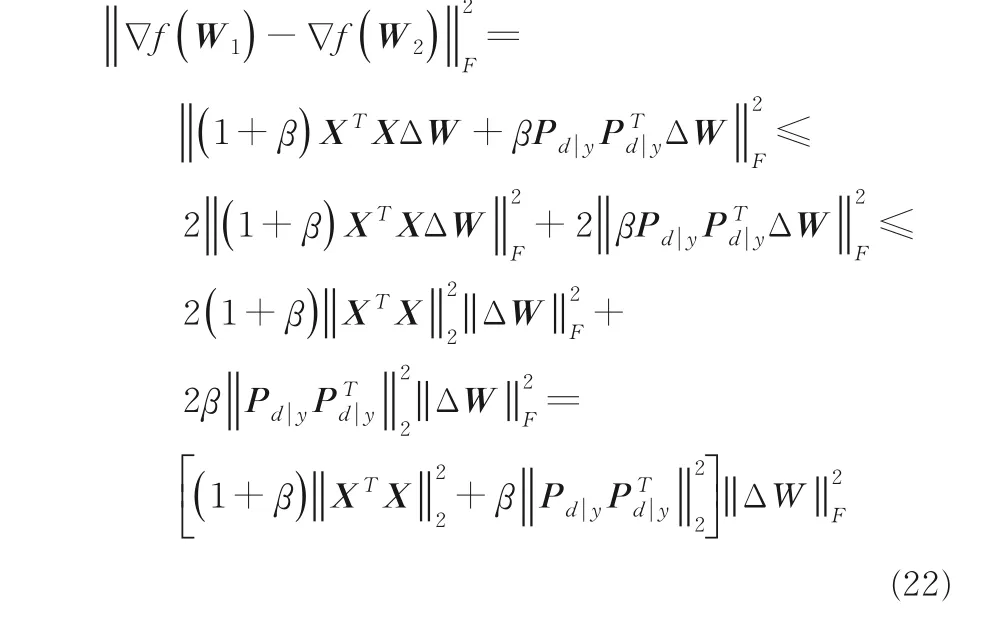
因此，该模型的Lipschitz 常数为：

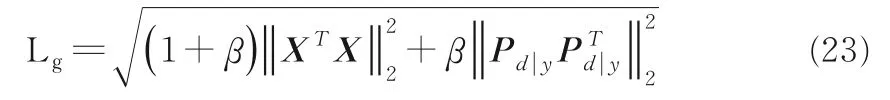
最后，计算对角奇异值矩阵Py，对角线的值分别为每个标签的奇异值.初始对角矩阵对角线的值为随机值，按照式（24）进行迭代，每次只选取对角线上的值：

2 PLSA-ML 算法框架及算法复杂度分析

2.1 算法框架本文提出的算法整体思路为首先用EM 算法对样本矩阵X进行无监督学习，获取赋有条件概率分布的语义矩阵Pd|y与Py|n.算法1 概述EM 算法，其中复杂度较高的为步骤5、步骤10 与步骤15.在步骤5 中，计算后验概率的算法复杂度为O(ndl2).步骤10 计算矩阵P|d y的算法复杂度为O(n2l2).在步骤15 中，计算矩阵Py|n的算法复杂度为O(nl).

算法2 概述加速梯度下降，其中复杂度较高的是步骤4 与步骤5.在步骤4 中，G(t)是一个中间变量，f(⋅)代表的是梯度，计算W的算法复杂度是O(nd2l+nl2+dl2).在步骤5 中，计算Lipschitz 常数的算法复杂度为O(nd2+d2l).

算法3 概述PLSA-ML 的算法流程，其中复杂度较高的为步骤3 与步骤5.步骤3 计算矩阵Py的算法复杂度为O(ndl2).步骤5 的算法复杂度为O(ndl2+n(d2+l2)+dl(d+l)).

2.2 算法复杂度及对比综上所述，本文提出的P LSA-ML 算法复杂度为O((ndl+dl)(d+l)+n(d2+l2)+n2l2).为综合体现PLSA-ML 的性能，将本文算法与LSML 和GroPLE 进行算法复杂度对比.根据文献［5，19］，LSML 的算法复杂度为O((n+l)d2+(n+d)l2+ndl+d3+l3)，GroPLE 的算法复杂度为O(nlg+g3+ng2+lg2+2ndg+dg2)，g代表嵌入潜在空间的维数.虽然本文的算法复杂度略高于LSML 和Gro-PLE，但实验结果表明，与LSML 和GroPLE 相比，本文的PLSA-ML 在多数文本类型的多标签数据集上有更好的分类效果.

3 实验方案及评价指标

3.1 多标签文本类数据集为体现本文算法的有效性，选取16 个来自雅虎与木兰网中具有文本属性的多标签数据集，具体描述见表2.因原有的PLSA 是挖掘文本潜在语义的相关模型，故在3.4节选取13 个多标签文本数据集进行对比实验.为体现本文算法的应用广泛性，在4.1 节介绍在其他类型多标签数据集的对比实验结果.

3.2 对比的算法及参数设置实验选取五个多标签分类算法与PLSA-ML 进行比较.GroPLE［5］是一种将特征组与标签组嵌入到低维空间的多标签分类算法.LSML［19］通过学习高阶标签相关性矩阵与类属属性处理缺省数据集的多标签分类.LSF-CI［10］是通过学习特征间相关性信息与标签间相关性信息提升类属属性学习的多标签分类算法.LLSF［9］是通过学习标签间的余弦相似度提升类属属性学习的多标签分类算法.FF-MLLA［20］是通过计算距离来度量样本间相似度，找到近邻点，然后结合标签近邻点和萤火虫方法对标签计数向量进行改进的多标签分类算法.

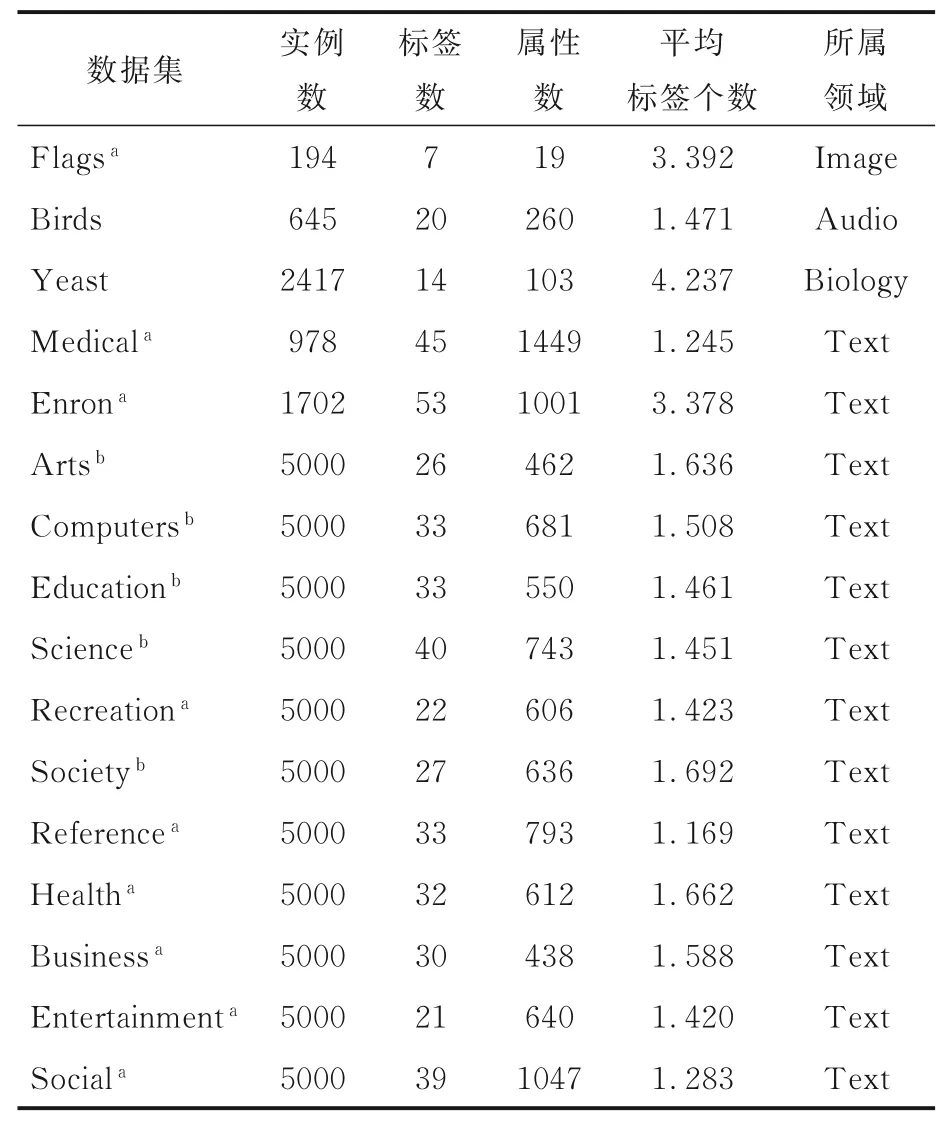
表2 数据集描述Table 2 Description of datasets

本文算法的参数设置为α∈[2-10，210]，β∈[2-10，210]，θ∈{1，10，100}.GroPLE 的参数设置为α∈[10-4，104]，β∈[10-4，104]，γ∈[10-2，102]，λ1∈[10-3，102]，λ2∈[10-3，102].LSML 算法中λ1，λ2，λ3，λ4参数设置为[10-5，103].LLSF 的参数设置为α∈[2-10，210]，β∈[2-10，210]，γ∈{1，10，100} .LSF-CI的参数设置为α∈[2-10，210]，β∈[2-12，212]，γ∈{0.1，10}，θ=2-8，谱聚类数目为10.FF-MLLA 的参数设置为聚类数目15，核参数100.

3.3 评价指标选择六种广泛使用在多标签分类的评价指标［21-23］分别与上述多标签分类算法进行对比.多标签数据集D={Xit，Yil|1≤t≤d，1≤i≤n，1≤l≤L}，h(⋅)是多标签分类器，f(⋅)是预测函数，rankf是排序函数.六种评价指标的定义如下：

海明损失可体现对被评估的对象标签错误分类标签的次数情况、正确标签错误预测情况：

其中，Δ 指两个集合之间的对称差.当海明损失为零时是最好的情况，即HLD(h)越小，h(⋅)的性能越高.

1-错误率可体现对被评估的对象最高排位并未正确标签的次数情况：

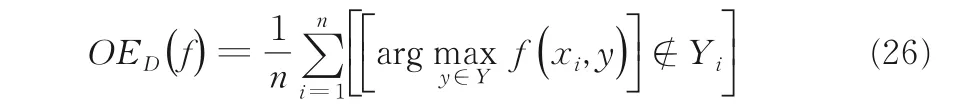
当1-错误率为零时是最好的情况，即OED(f)越小，f(⋅)的性能越高.

覆盖率可体现被评估对象标签序列中所需标签数达到覆盖全部标签的情况：

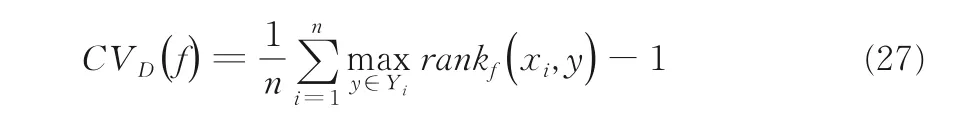
CVD(f)越小，f(⋅)的性能越高.

排序损失可体现被评估对象非属标签的排位高于所属标签的次数情况：

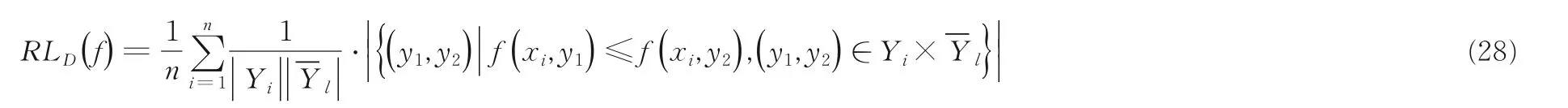
当排序损失为零时是最好的情况，即RLD(f)越小，f(⋅)的性能越高.

平均精确是评估在特定标签y∈Yi排列的正确标签的平均分数：

当平均精确值达到1 时是最好的情况，即APD(f)越大，f(⋅，⋅)的性能越高.

ROC 曲线上的平均面积（AUC）是一个在所有标签上取平均值，然后统计出正标签排名高于负标签的分数：)

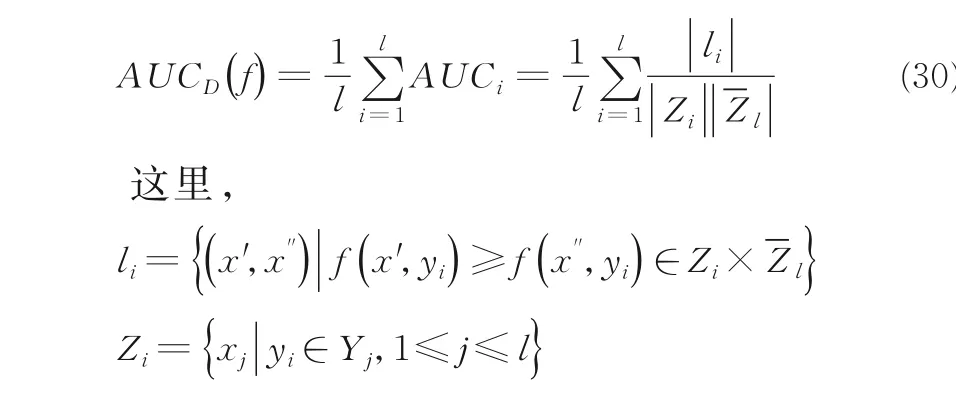
AUC的分数越高，说明算法的性能越高.

3.4 文本类数据集实验结果分析采用五折交叉验证法评估算法表现.五折交叉验证将所有数据随机分到五个相等的子集中，每个子集依次被测试，而其他剩余的数据用于训练.因五折交叉验证是迭代五次，故需计算五次运行的平均值.

表3 至表8 是本文提出的算法与其他对比算法在六种评价指标上的实验结果对比，黑体字表示最优的实验结果，算法的平均排序越低越占优.可以看出：

（1）PLSA-ML 模型不仅考虑特征-标签之间关系，还考虑标签-实例之间关系，因而实验结果大部分占优.

（2）实验结果表明，与同样考虑特征-标签之间关系的算法相比较，PLSA-ML 学习它们之间的条件概率分布矩阵，可以使算法更好地理解它们之间的关系.

（3）在AUC指标上，PLSA-ML 表现较差，说明本文算法不擅长处理正负类标签问题.

综上，本文的PLSA-ML 学习特征-标签与标签-实例条件概率分布信息存在一定合理性.

表3 各算法在13 个数据集上的海明损失Table 3 HL of different algorithms on 13 datasets

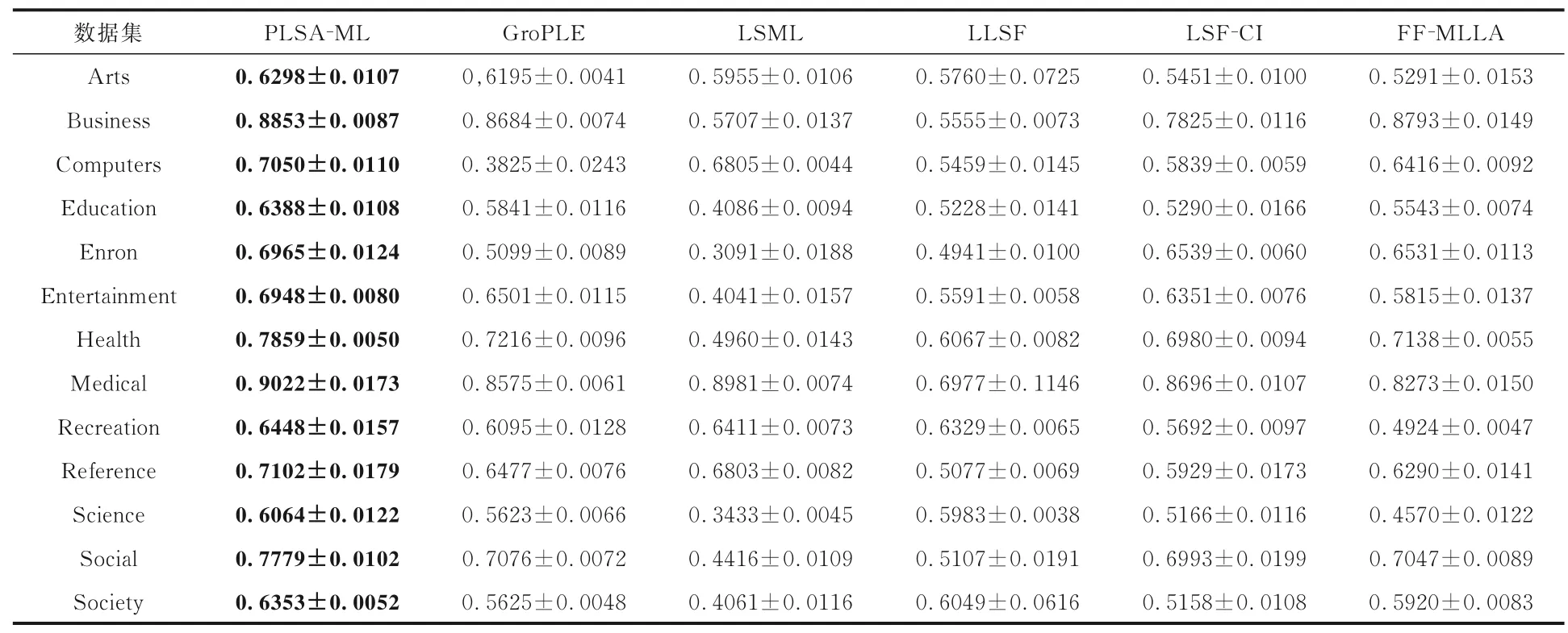
表4 各算法在13 个数据集上的平均精度Table 4 AP of different algorithms on 13 datasets

4 算法性能分析与参数敏感度

4.1 算法应用广泛性测试选取两个新型多标签算法与PLSA-ML 在图像、生物与声音类型的多标签数据集进行对比实验，并在三种评价指标上显示算法的性能.图3 展示各算法在AP，OE与CV评价指标上的性能，发现PLAS-ML 在其他类型的多标签数据集的分类效果也较好，所以图像与生物等类型多标签数据集中特征-标签与标签-实例可能符合一种条件概率分布.在PLSA模型中，这种条件概率的存在属于哪种语义信息，如何进一步应用是未来要研究的问题.

表5 各算法在13 个数据集上的1-错误率Table 5 OE of different algorithms on 13 datasets

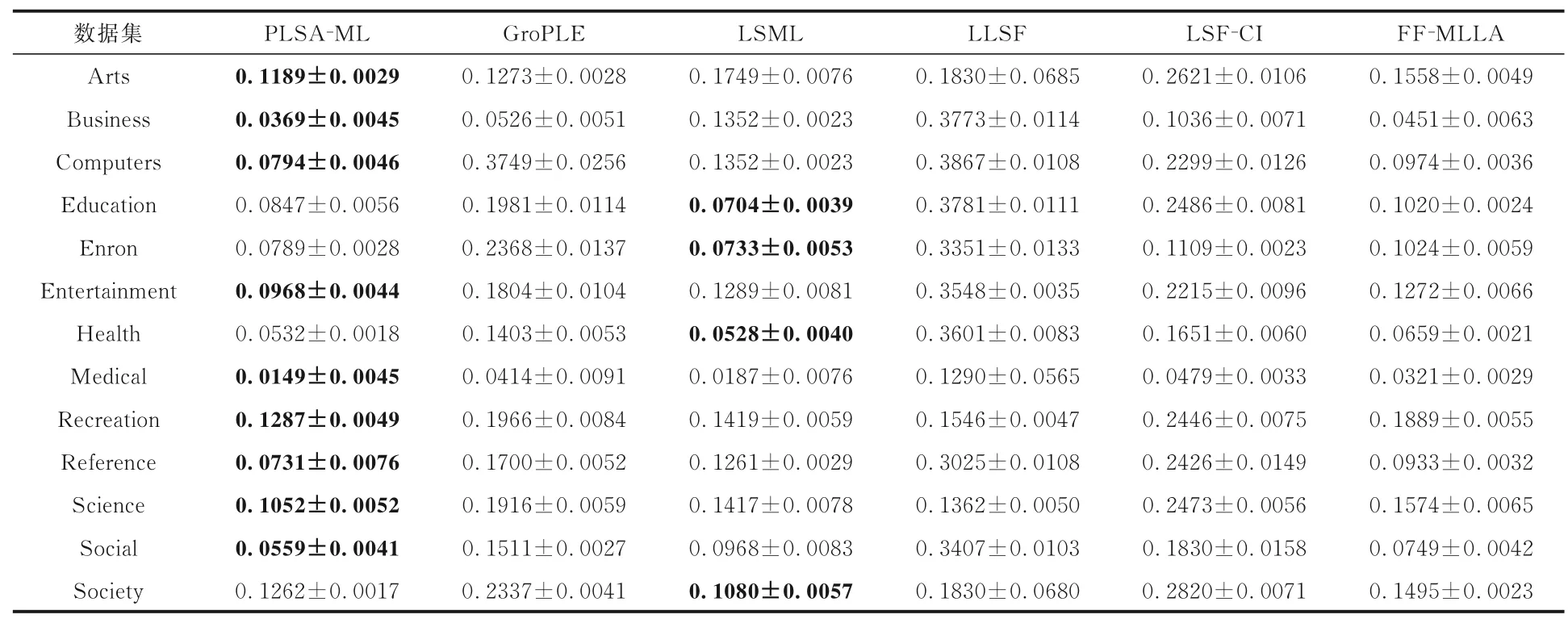
表6 各算法在13 个数据集上的排序损失Table 6 RL of different algorithms on 13 datasets

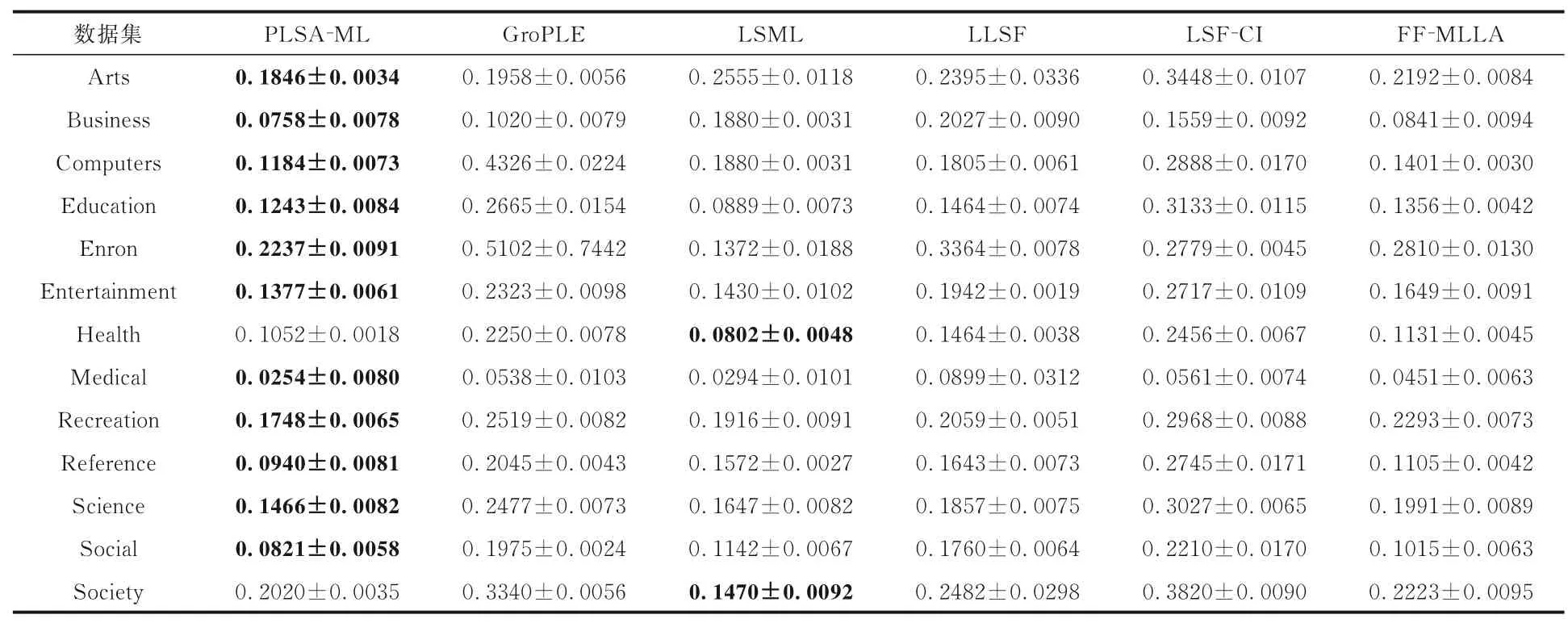
表7 各算法在13 个数据集上的覆盖率Table 7 CV of different algorithms on 13 datasets

表8 各算法在13 个数据集上的AUCTable 8 AUC of different algorithms on 13 datasets

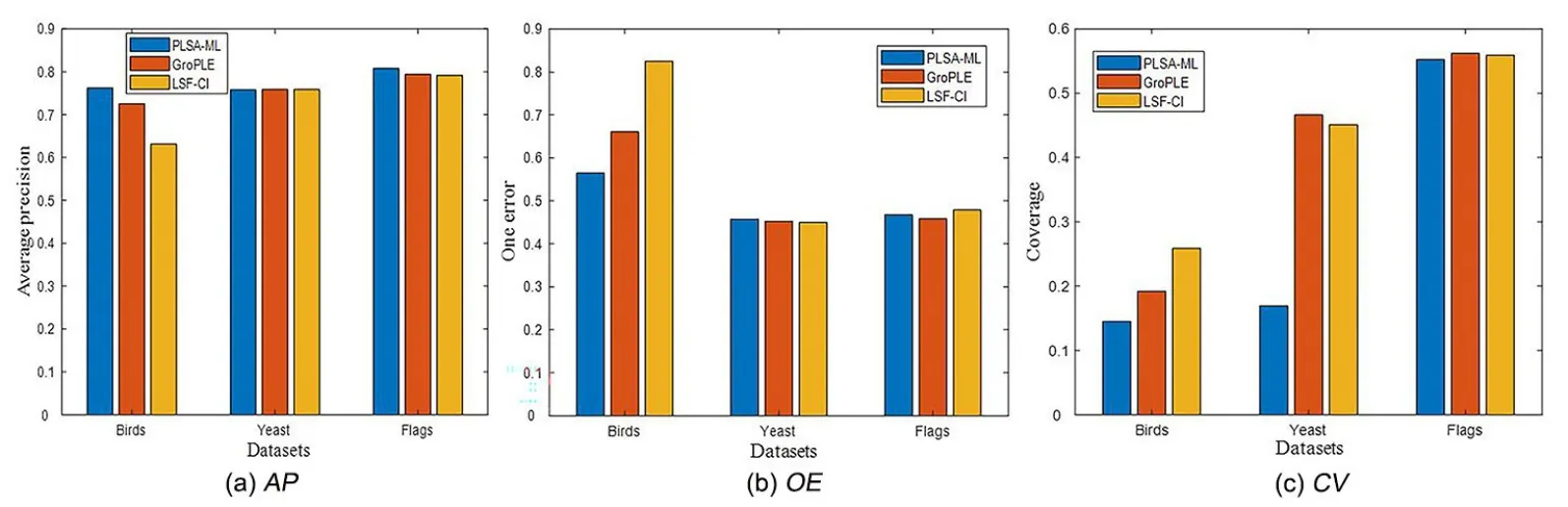
图3 图像、生物与声音类型的多标签数据集下的实验结果Fig.3 Images with biological types of multi-label data sets under experimental results

4.2 EM 算法收敛性分析及证明本文在挖掘特征-标签与标签-实例条件概率分布矩阵时，利用到EM 算法中最大化对数似然的期望.当对数似然值收敛时PLSA-ML 模型的EM 算法迭代停止，可以得到上述的条件概率分布矩阵.图4a 和图4b 是PLSA-ML 在Business 与Medical 多标签文本数据集上的对数似然值收敛曲线，可以发现PLSA-ML 模型中的EM 算法具有收敛性，迭代次数达到90 到100 次后对数似然值收敛.

下面证明在本文框架上EM 算法的收敛性，只需证明对数似然函数值在迭代过程中是增加的.用δ代表EM 算法迭代参数，xij代表样本矩阵中每个实例.即证：

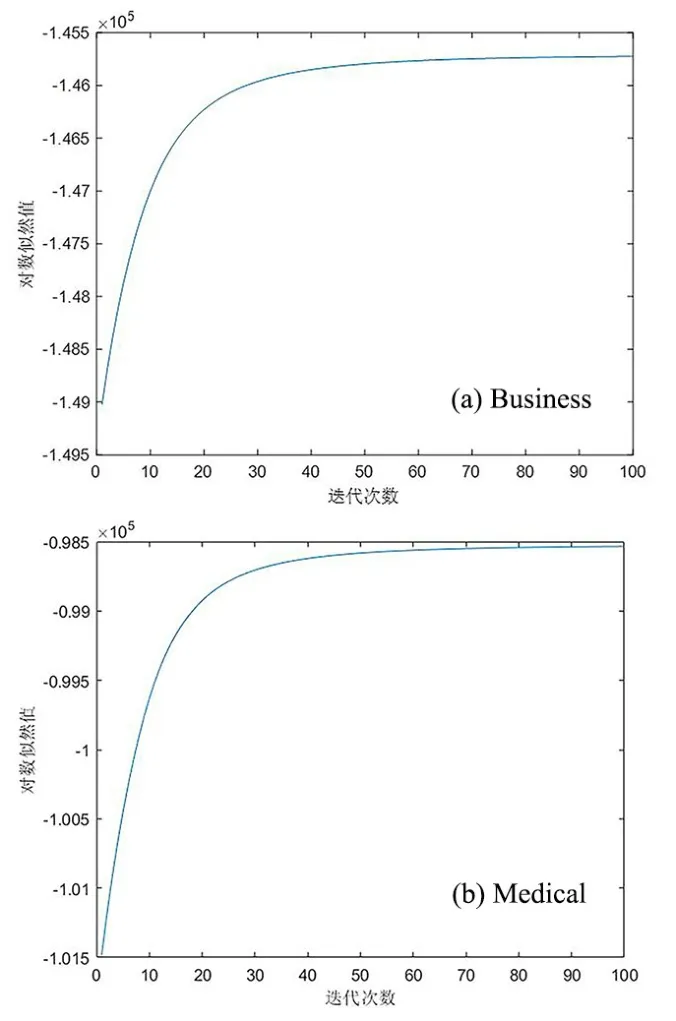
图4 PLSA-ML 在Business 和Medical 数据集上的对数似然值收敛曲线Fig.4 Log-likelihood convergence curve of PLSA-ML on Business and Medical datasets

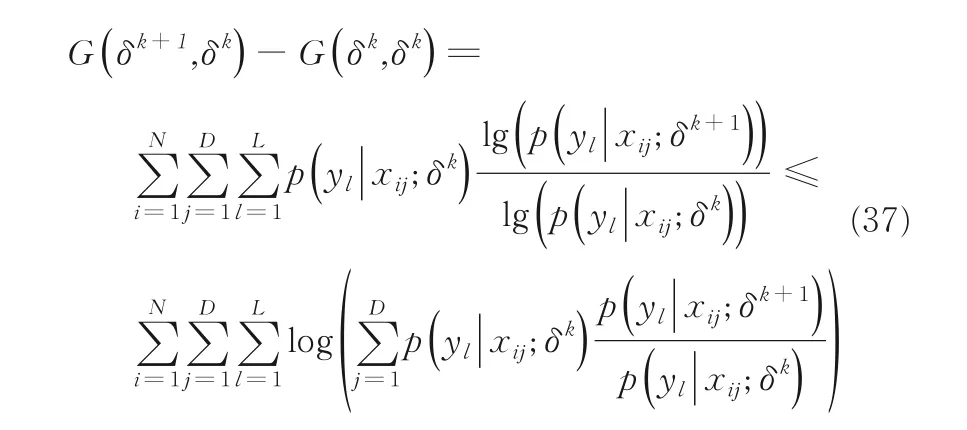
问题得证.

4.3 参数敏感度分析本文的PLSA-ML 算法模型中有两个参数α，β.参数α可控制矩阵W的稀疏性，进而控制算法特征选择的强弱.参数β可控制学习语义信息的损失.为了测试上述参数对PLSA-ML 算法的影响，在Medical 数据集上进行参数敏感度分析.从图5 可以发现，当参数α，β取中间值时算法的性能较好，而当参数α，β超过中间值时，算法的性能开始变差.参数α的变大导致算法提取的特征变得十分稀疏，参数β变大可以导致PLSA-ML 算法获得概率语义信息变得十分稀少.

5 条件概率分布可视化及统计假设检验

5.1 条件概率分布可视化图6a 和图6b 分别显示本文PLSA-ML 模型Business 与Medical 多标签文本数据集上的特征-标签条件概率分布矩阵Pd|y.通过将概率分布矩阵可视化，可以发现语义信息以一定的概率分布形式存在于矩阵Pd|y.实验结果表明多标签算法学习这些语义信息，可以提升算法的性能.不难发现，图6a 中的特征与标签少于图6b 中的特征与标签，导致图6a 中的语义信息少于图6b，这表明对于特征与标签较少的数据集，这种语义信息稀疏的可能性较大.具有丰富语义的多标签文本数据集可以为PLSA 模型获取更多的语义信息，这同样是本文建立PLSAML 模型的初衷.PLSA 模型可以挖掘出较多的潜在于多标签文本数据集中的语义信息，为特征与标签间联系赋予较好的数学模型与数学解释.

为了测试学习条件概率语义的必要性，将模型中学习条件概率语义信息的损失项删除，与本文算法进行对比实验.表9 显示HL与RL评价指标的对比实验结果，黑体字代表算法表现优异，A代表本文提出的PLSA-ML 模型，B 代表删除条件概率语义信息损失项的模型.可以发现，A 的HL指标在多个数据集上占优，RL指标则全部占优.因此，多标签模型学习概率分布语义信息可以提升自身的性能.

5.2 统计假设检验为了分析算法之间在不同多标签文本数据集的性能，采用非参数化的弗里德曼检验［19］.弗里德曼检验用于评估在每个评价指标下，所有数据集上每个算法的平均排序是否与所有算法等价的假设下的平均排序有显著性差异.在每个指标上根据表3 至表8 对算法从低到高进行排序，再对每一列的数值计算平均值得到平均排序.具体算法对比情况可见表10，表中的黑体字代表算法性能占优.实验涉及的算法有六种，多标签文本数据集有13 个.因此，F-分布的自由度为(6-1)与(6-1)×(13-1)=60.在表11 中，弗里德曼统计值依照显著水平α=0.05 的每个评价指标值计算，临界值根据F(5，60)选取.可以明显发现，每一个评价指标都拒绝零假设.

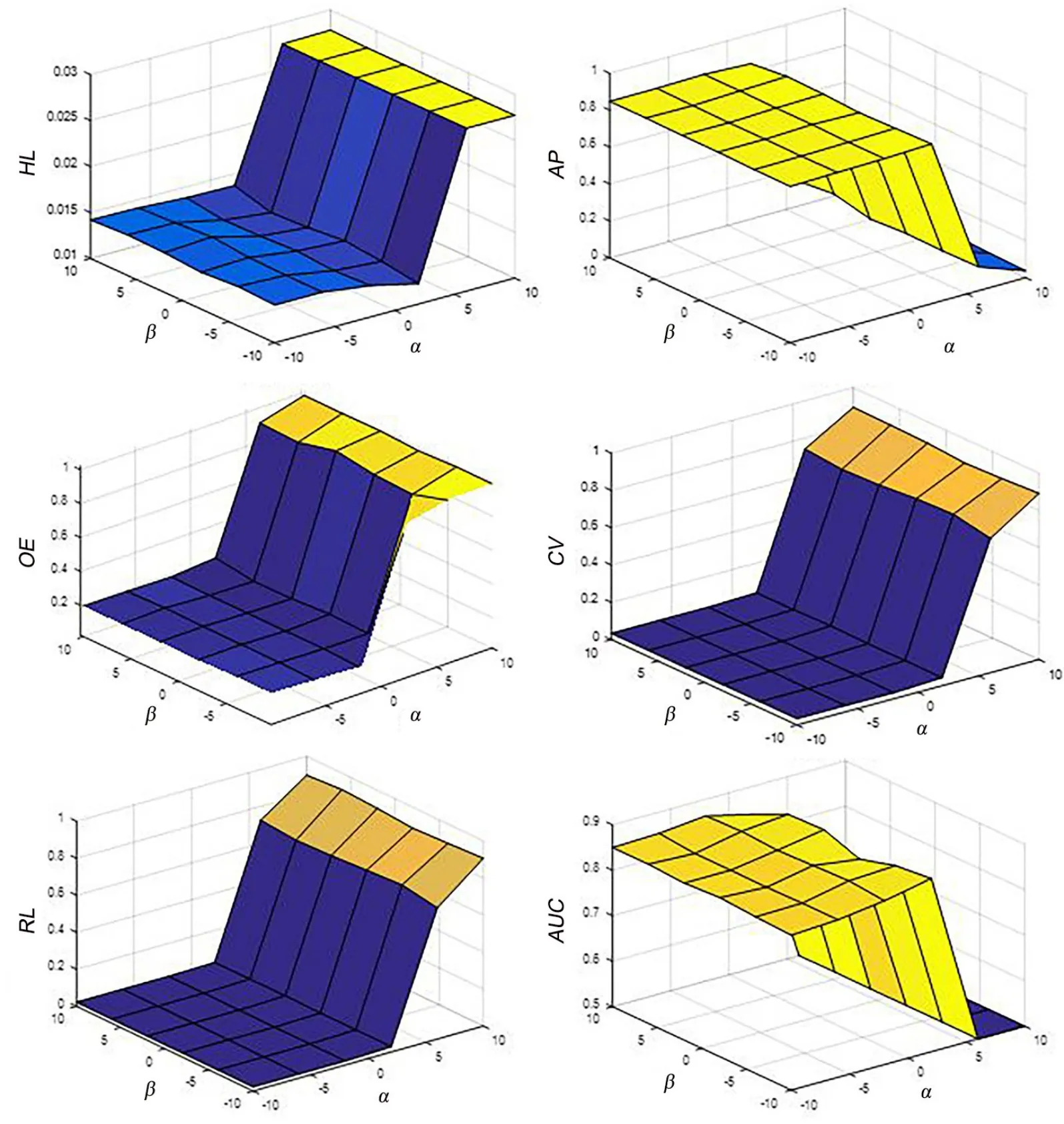
图5 PLSA-ML 算法在Medical 数据集上的参数敏感度分析Fig.5 Parameter sensitivity analysis of PLSA-ML on Medical datase

图6 PLSA-ML 算法在Business 和Medical 数据集上的特征-标签条件概率分布Fig.6 Feature-label conditional probability distribution of PLSA-ML on Business and Medical datasets

表9 测试条件概率语义信息的参考性Table 9 Test the reference of conditional probability semantic information

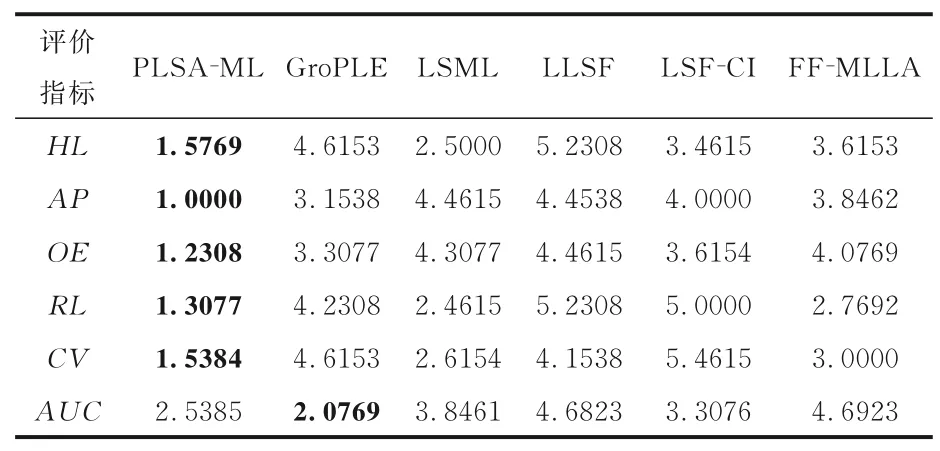
表10 各个算法在不同评价指标上的平均排序Table 10 The average ranking on different evaluation indicators of various algorithms

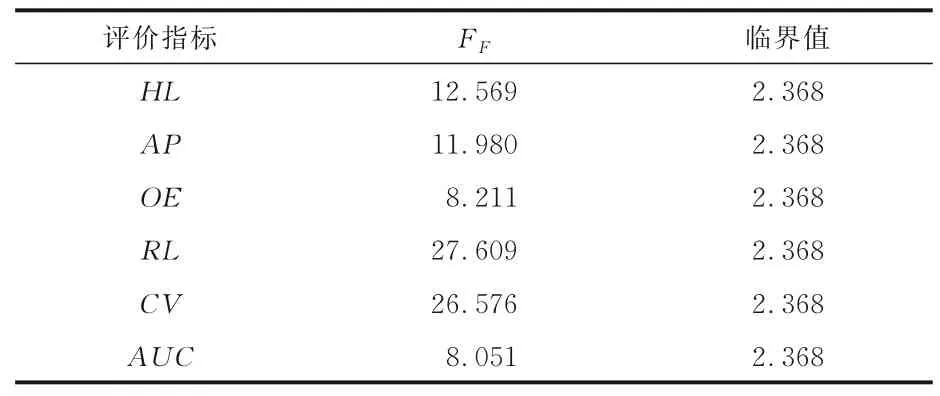
表11 每个评价指标的弗里德曼统计值和在α=0.05 以及F(5,60)时的临界值Table 11 Summary of the Friedman statistics on each evaluation metric and the critical value of F(5,60)for α=0.05

由于通过弗里德曼检验得知所有评价指标都拒绝零假设，所以本文采用Nemenyi 检验［24］测试PLSA-ML 与其他算法的性能.不同的两种算法依据临界差值（critical difference）进行比较：

其中，显著水平α=0.05，k=6，N=13，qα=2.850，因此，CD=2.0913.由图7 可知，PLSA-ML 与其他多标签算法比较总体是占优势的.PLSA-ML的HL评价指标与LLSF 和GroPLE 差异显著；AP评价指标与其他算法差异显著；OE评价指标与LLSF，LSF-CI，LSML 和FF-MLLA 差异显著，RL与CV两种指标与LLSF，LSF-CI，Gro-PLE 算法差异显著；AUC评价指标，虽然Gro-PLE 与FF-MLLA，LLSF 差异显著，但PLSAML 与GroPLE 无显著差异.通过统计假设检验进一步证明了本文PLSA-ML 算法性能的有效性，学习特征-标签与标签-实例条件概率分布语义信息的合理性.

6 结论

在多标签文本数据集中特征空间与标签空间都含有丰富的语义信息，语义信息的挖掘与应用是目前研究的热点.受PLSA 模型中文本、单词与主题之间联系的启发，本文提出基于PLSA 学习概率分布语义信息的多标签分类算法（PLSAML），将特征与标签、标签与实例以条件概率分布的形成呈现.样本矩阵中存在一种标签隐含变量，进而利用PLSA 模型赋予特征与标签、标签与实例的联系逻辑结构，并建立多标签模型学习获取的条件概率分布矩阵的语义信息.实验证明，PLSA-ML 学习特征-标签、标签-实例条件概率分布的语义信息，可以较好地提升算法的性能.虽然PLSA-ML 在其他类型的多标签数据集上进行实验也得到较好的分类效果，但尚未有较好的解释，这是未来研究的问题.多视角下的多标签数据集的语义分析同样是值得研究的问题.

图7 PLSA-ML 与其他算法的Nemenyi 检验(α=0.05)Fig.7 The Nemenyi test(α=0.05)of PLSA-ML and other algorithms