基于图像校正和模板分割的纺织品瑕疵检测

马明寅 ,狄 岚,2* ,梁久祯

（1.江南大学人工智能与计算机学院，无锡，214122；2.道路交通安全公安部重点实验室,无锡，214151；3.常州大学信息科学与工程学院，常州，213164）

在纺织品的生产过程中，质量的控制与检测非常重要.目前，由于人工手动操作检测瑕疵是大多数工厂的检验方式.但这种方式工作强度过大，缺乏客观性，受外界干扰的因素较多，效率较低，检验的错误率也较高.人力成本的提升使生产自动化越来越受到人们的关注.纺织品大致可以分为纯色的无图案纺织品与有图案的纺织品.无图案的纺织品，样式朴素，没有复杂的花纹，常为平纹和斜纹；有图案的纺织品，结构复杂，包含复杂的图案，大部分含图案的纺织品都具有水平与垂直方向上的周期变化特性，瑕疵的类型较多.本文主要研究针对图案含有复杂周期性变化的纺织品的瑕疵检测.

现阶段对于纺织品瑕疵检测的方法主要分为统计学方法［1-3］、光谱的方法［4-6］、模型的方法［7-8］、学习的方法［9-10］和结构的方法［11］.而其中布林线波段法（Bollinger Bands，BB）［12］、正则带法（Regular Bands，RB）［13］、Elo 评分方法（Elo Rating，ER）［14］、基于小波预处理的黄金图像减法（Wavelet preprocessed Golden Image Subtraction，WGIS）［15］和基于模板校正的方法（Templatebased Correction，TC）［16］，处于目前该领域研究的领先地位.

在图像校正的领域中，赵卓等［17］在2004 年针对性建立了在视觉增强环境下校正图像的模型，并提出利用边缘检测进行自动校正的方法；之后胡东红等［18］在2009 年介绍了透视变换和控制点变换两种图像校正方法，分析了两种方法的特点和差异，并讨论了两种方法在实际情况中的应用，得出了在复杂情况下透视变换的校正效果好于控制点变换的结论；此外，龚俊等［19］在2015 年提出一种采用彩色四元数边缘特征矩阵计算图像边缘的梯度幅值，以精确地提取图像边缘的基于四元数理论的Canny 改进算法，保留了更多原始图像的信息，降低了噪声的影响.而在瑕疵检测的研究方向中，赵树志等［20］在2018 年提出一种改进判别性完整局部二值模式（discriminant Complete Local Binary Pattern，disCLBP），结合自动格分割的织物瑕疵检测方法，解决传统的完整局部二值模式（Complete Local Binary Pattern，CLBP）在织物疵点检测时存在直方图维数过高和特征冗余，并在小区域图像变化幅度剧烈或变化幅度平缓时存在局限性的问题.2019 年狄岚等［21］在前者的基础上针对光照对纺织品图像特征提取的影响以及传统完整局部二值模式算法的局限性，对比了不同预处理方法对于光照影响下的图像检测效果，并提出一种基于局部对比度增强算法的改进特征提取方法.

但目前较多方法，如WGIS，ER 等，都需要以一块确定的模板为基准，甚至是以人工选取的方式规定模板，但这样的模板有一定的特殊性，不能较好地适用于所有图像.而在基于相似关系的方法（Similarity Relation，SR）［22］中，周期计算的自适应分割方法和TC 方法的模板校正虽然解决了人工选取和图像内模板差异的问题，但依然忽略了图像本身的不规则以及图像之间的模板差异问题.

针对以上问题，本文从原始图像的不同特点出发，为尽量缩小图像之间的差异，提出一种基于图像校正和模板匹配的纺织品瑕疵检测方法.首先将图像进行Hough 变换，并依据直线结果进一步将图像进行透视变换，以达到将图像校正为具有明确周期规律和符合边界特征的规则图像的目的.再利用周期分割和模板校正的方法选取模板，对于低秩分解之后的图像使用黄金图像减法（Golden Image Subtraction，GIS）作为瑕疵检测方法，最终标记出纺织品的瑕疵部分.

1 相关工作

1.1 Hough 变换Hough 变换是一种通过投票原理来实现的参数估算统计算法，利用图像空间和参数空间的点线对偶性，将图像空间的检测问题转换到参数空间中.具体来说，将图像空间中的x-y坐标系的一条直线L0：y=k0x+b0上的两点P1(x1，y1)和P2(x2，y2)，对应参数空间中的k-b坐标系，产生两条直线：

两条直线的交点P0(k0，b0)则对应图像空间中的直线L0.针对直角坐标系中斜率k有无穷大的情况，Hough 变换将x-y坐标系的图像空间对应到以ρ-θ为坐标系的参数空间中，则有P1(x1，y1)和P2(x2，y2)对应的参数方程：

其中，ρ为直线到原点的距离，θ为x轴到直线垂线的角度.两条曲线的交点P0(ρ0，θ0)就对应为图像空间中的直线L0.

将参数空间离散化为许多小格，采用“多对一”映射，计算图像空间中共线的像素点在参数空间中对应的参数值.若计算结果落在某一小格内，就使该小格的累加器加1，累积值最大的小格即为图像空间中直线的参数［23］.把检测到的峰值及一定范围内的邻域值归零，然后继续检测，直到检测出所有直线为止.

1.2 透视变换透视变换是指在透视中心不变的条件下，将透视面绕透视轴旋转某一角度，把已有的图像投射到另一个空间平面上，但在新的平面上图像的垂直投影仍能保持不变.

透视变换的通用公式为：

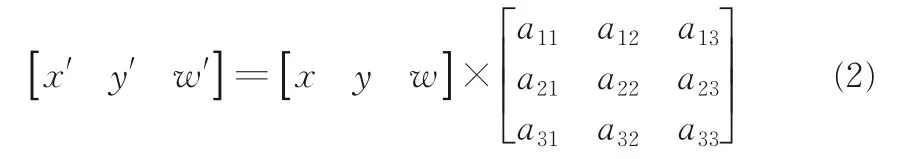
(x，y)为原始图像像素坐标，(u，v)为变换之后的图像像素坐标.则有：

2 基于图像校正和模板匹配的算法

本文的算法主要分为训练部分和检测部分.

训练部分：将无瑕疵的纺织物图像进行校正后，使用周期分割算法将无瑕图像分块，并将所用同类型的无瑕图像的分块进行模板校正.以此图像作为黄金图像模板，对所有同类型无瑕图像进行低秩分解之后，使用黄金图像减法，计算每幅图像中能量的最大值，并将所有最大值的最小值作为阈值.

检测部分：将有瑕疵的纺织物图像进行校正，并用训练部分中得到的黄金图像作为模板，将低秩分解之后的瑕疵图像进行黄金图像减法，将检测图像得到的能量与阈值作对比，大于阈值的部分则标记为瑕疵.

算法流程如图1 所示.

图1 算法流程图Fig.1 Flow diagram of overall algorithm

2.1 图像校正

2.1.1 校正的定义通过对实验数据的观察可以发现，无论是无瑕疵的纺织品图像还是有瑕疵的纺织品图像，都有不同程度的偏移和倾斜，并不是以完整方正的各个单元的组合呈现在图像中.根据不同的偏移方向和倾斜角度将所有图像分为拉伸、剪切、旋转三个类型，并针对其不同的特点做出不同的变换，以达到将偏斜的图像转换为单元方正的图像的目的.

2.1.2 图像校正算法由于不同图像的偏移方向和偏移量以及倾斜角度和倾斜量难以直接确定，本文使用Hough 变换，将图像中的直线具象化，以直线的偏移和倾斜来判定图像需要修正的方向和像素值.将最靠近四周的四条完整直线的四个交点设置为移动点，以直线与边缘的交点的横纵坐标确定的位置作为目标点.再根据上文中确定的不同类型的偏斜图像，使用不同的变换方式将图像校正.具体算法步骤如下：

（1）输入偏斜的图像，使用Canny 算子对图像进行预处理，标记图像的边缘，利于直线的识别.

（2）依照处理后的图像，使用Hough 变换，将图像中所有的直线标记出来，并突出显示离四周最接近的四条完整直线.

（3）将四条直线的交点设为移动点；以移动点为基准，再以横向直线与反方向边缘交点的横坐标为横坐标，纵向直线与反方向边缘的交点的纵坐标为纵坐标，设为与移动点相对应的目标点.

（4）根据不同的偏斜类型，使用不同的变换方法，输出校正后的图像.

本文使用的变换方法主要以透视变换为主，针对不同的偏斜图像选取不同的对应点组：图像为拉伸类型时，选取不在拉伸对角方向上的两组对应点进行变换；图像为剪切类型时，选取与剪切方向同向的两组对应点进行变换；图像为旋转类型时，则需要使用全部四组对应点进行变换.

透视变换至少需要四组对应点，而纺织品瑕疵检测的图像大多为正方形，因此本文使用图像的四个角点作为基准点.在进行变换时，除了上文选取的不同的对应点组之外，若还未达到四组的标准，则使用除去距离对应点最近的剩余的基准点.此时，基准点不需要移动，即基准点同时为移动点，也为目标点.

在透视变换时，式（2）中的变换矩阵：

在实际计算中，将变换矩阵T中的九个参数分别设置为A～I，将式（3）变式则有：

其中，(x，y)为原始图像像素坐标，(u，v)为变换之后的图像像素坐标.将I设定为1，并将式（5）矩阵化，则有：

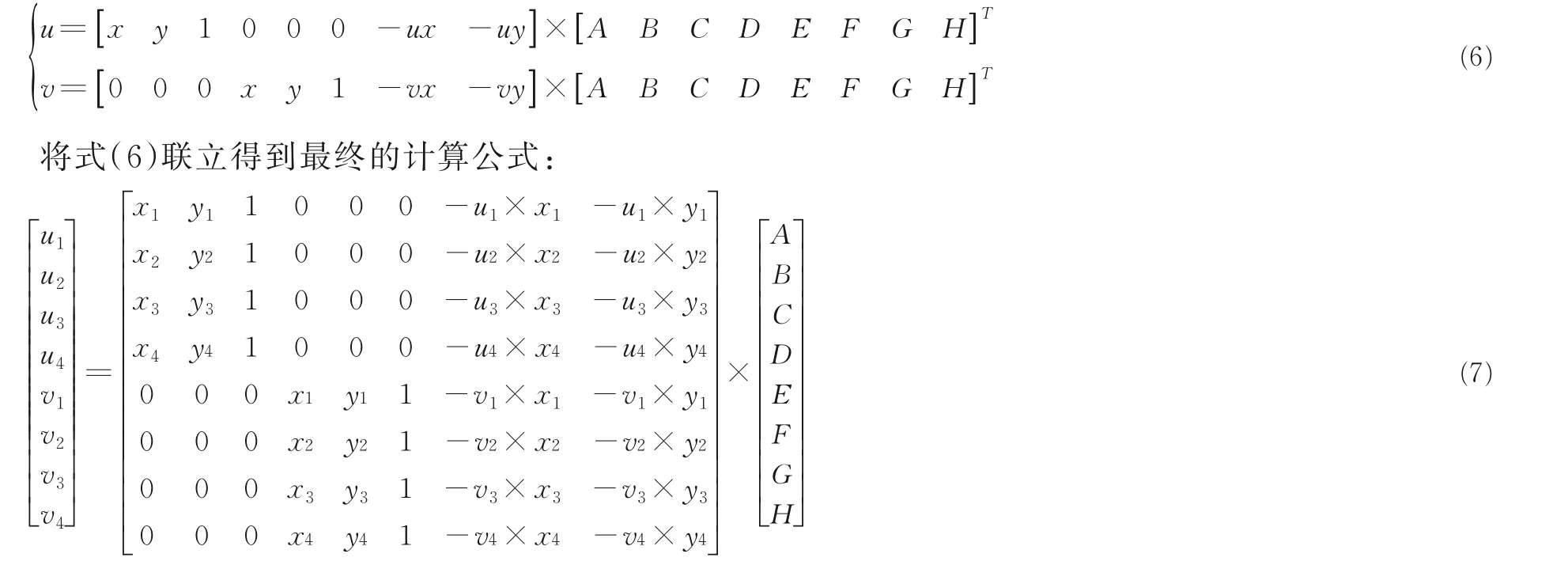
用已知的四组点的坐标代入式（7），则可以计算出变换矩阵：

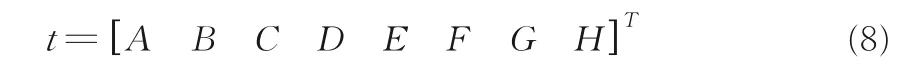
再将整张图像与矩阵t相乘，就可以得到校正后的图像，如图2 所示.

2.1.3 针对星形图的图像校正本文主要通过Hough 变换提取图像中的直线来作为进一步校正的依据，但在实际应用中箱形图较容易展现出图像中的直线，而星形图则较难显现.因此本文的图像校正方法中，针对于星形图在校正之前增加了预处理环节：使用类似黄金图像减法（GIS）的方法，将星形图中的每个星形单元转换为对应位置的点，即将整张图像转变成点阵图.关于GIS方法的具体过程见2.5，在此阶段中与GIS 方法选取同样的模板，不同之处在于使用不同的阈值：GIS 方法使用的阈值目的是区别出瑕疵与背景的部分，而本环节中使用阈值的目的是将星形图中的星形单元转换为点.如图3 所示.

由点阵图再使用2.1.2 的图像校正方法，得到相应的变换矩阵，再应用到原星形图，就可以得到校正后的图像.

图2 图像的校正效果Fig.2 The correction effect of orginial image

图3 星形图转换为点阵图Fig.3 Dot plot transfered from star pattern

2.1.4 图像插值方法经过上文的方法将图像校正之后会丢失一部分的细节信息，在瑕疵检测的过程中会产生一定的影响.为了尽量减少相关的影响，本文使用图像插值的方法，对于校正算法进行预处理和结果处理.

图像校正前，先将待校正图像的行列分别进行插值处理，分辨率扩大为原图的4 倍.对扩大之后的图像进行校正，校正完成后再以相同插值方式将图像还原为初始尺寸，用以进行后续操作.

对于不同的插值方式，如最近邻插值、双线性插值、双三次插值和箱型插值，处理之后的图像检测结果也都有不同的影响，针对以上几种方法，本研究也完成了相应的对比实验.

2.2 周期计算针对有图案的纺织品具有明显周期性的特点，可以将整幅图像分割成大小相同的众多单位图像.本文使用一种基于方差分析的周期计算方法［22］，对于一张具有周期变化规律的图像I，满足下式：

其中，(r*，c*)为理想的单位图像尺寸.从图像I中选取尺寸为r×c的方格，当所有格子与灰度均值矩阵中相应的像素点灰度值的标准差的和达到最小时，(r，c)取到理想大小(r*，c*).损失函数f(r，c)定义为：

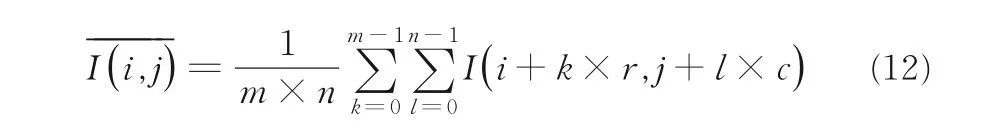
当所有图像块之间的方差和最小时，即能得到理想的周期.

2.3 模板校正

2.3.1 校正方法图像在进行周期分割后，各幅图像间的方格存在不匹配的现象.为了减少这种情况的影响，提出一种模板校正的方法［16］.分割后的大多数方格都包含每个周期图案的完整信息，并且每个方格都是数字构成的矩阵，不匹配的原因在于各幅图像的方格之间行列的排布顺序不一致.因此可以使用循环移位的方法，来尽可能地将方格之间的差异最小化.提出以下模型：

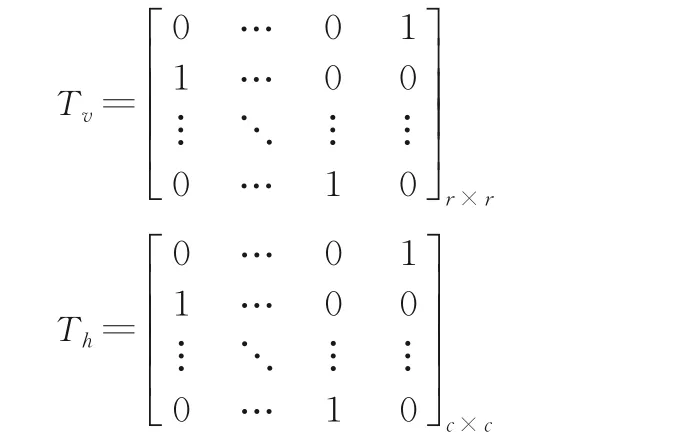
其中，A为待校正的方格，B为标准方格，p*表示行变换的次数，q*表示列变换的次数，p*∈[0，r-1 ]，q*∈[0，c-1 ]，Tv与Th分别是大小为r×r和c×c的两个矩阵，定义为：

通过式（13）计算出p和q，在水平方向上将A分割成q×r和()c-q×r两部分，并将前一部分移动到后一部分的右侧，从而完成水平方向的校正.同理，继续在竖直方向上做对应的操作便能得到校正后的方格.校正过程如图4 所示.

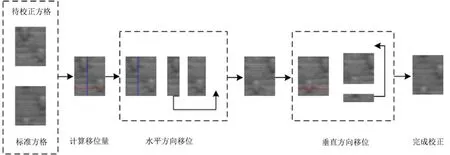
图4 模板校正流程图Fig.4 Flow diagram of template correction

2.3.2 建立模板将N幅无瑕图像依照周期进行分割后，计算每幅图像中所有方格的灰度均值矩阵，以此矩阵作为样本矩阵，定义为Pi，i=1，…，N.以第一幅无瑕图像的灰度均值矩阵P1作为标准方格，其余的方格均按照P1使用上文介绍的方法进行校正，对应校正后的方格记为Oi.模板TM定义为：

其中，x∈[ 1，r]，y∈[ 1，c].校正之后得到的方格对于每幅图像都有较好的普适性，更适合作为统一的模板.

2.4 低秩分解低秩分解是处理矩阵相关性的一种方法，而本文中具有复杂周期性的纺织品图像也是矩阵的一种，并且低秩分解是从图像的低秩性和稀疏性将其分解的方法，更加契合复杂图案的纺织品瑕疵检测［24］.

传统的低秩分解模型如下：

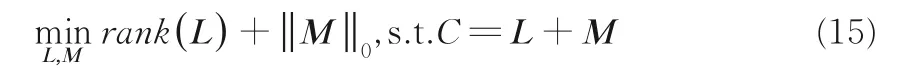
其中，L表示图像的低秩部分，M表示图像的稀疏部分.将原模型转化为易解的近似问题：

针对纺织品瑕疵图像具有周期性复杂图案的特点，传统模型中核范数对于不同大小的奇异值采用相同的收缩力度导致丢失了较多的信息，并且在分解的过程中没有重视瑕疵与背景的区别.因此本文对以上两点分别进行了改动.

使用β范数取代传统的核范数，对于不同的奇异值施加不同的权重，以突出图像的特征，同时将L1范数改为L2，1范数.β范数具体形式如下：

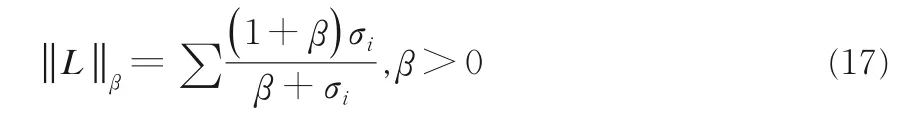
其中，σi为矩阵L的奇异值，β取0.001.L2，1范数的具体形式为：

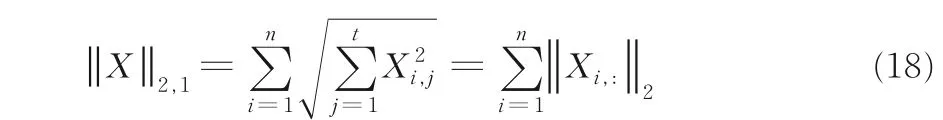
则最终改动后的模型为：

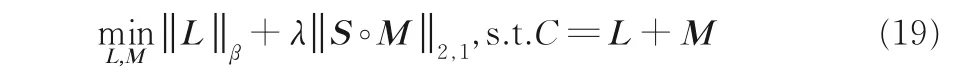
其中S为先验信息，∘为哈达玛乘积.

2.5 GIS 方法黄金图像减法（GIS）是一种传统的纺织品瑕疵检测的方法.其基本思想：对于一幅尺寸为R×C的无瑕图像I0，随机选择一块尺寸为r×c的区域L，要求该区域比一个无瑕图案尺寸略大.将区域L在待检图像I上逐个像素进行移动，每经过一个像素点时计算一次区域能量Exy，其定义为：

其中，x=1，2，…，R-r+1，y=1，2，…，Cc+1.Lij为区域L中第i行第j列的像素值，(Lxy)ij为待检图像中所选的r×c大小的区域Lxy第i行第j列的像素值.区域L与待检图像完成移动计算后获取的结果定义为矩阵E，E的每个元素是获取的能量Exy.

对w幅无瑕纺织品图像和区域L进行GIS 运算，可以获得w个能量图像，记为Ek.其中，k=1，2，…，w.

定义阈值T：

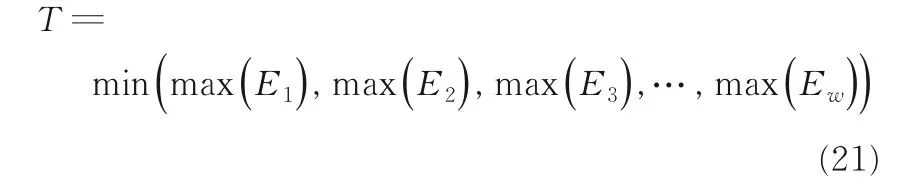
则对于任意待检测的有瑕疵图像I，

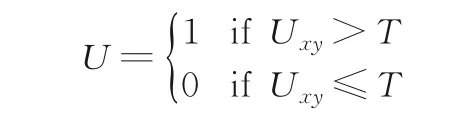
其中，x=1，2，…，R-r+1，y=1，2，…，Cc+1.Uij表示图像I中第i行第j列的像素通过GIS 方法得到的图像能量.若该像素点的图像能量大于阈值T，则被认为是瑕疵点而数值置为1，反之判定为无瑕像素，数值置为0.

2.6 算法流程本文的算法流程具体步骤如下：

训练部分：

步骤1：将无瑕疵图像进行校正，得到单元方正的图像.

步骤2：计算校正后的图像的方格周期，并以周期对图像进行分割.

步骤3：将分割得到的方格依照同一标准进行校正，并取其均值作为确定的模板TM.

步骤4：将校正后的无瑕疵图像进行低秩分解.

步骤5：以得到的模板TM 作为黄金图像，对低秩分解后的无瑕疵图像使用GIS 方法，得到决定瑕疵标准的阈值.

检测部分：

步骤1：将有瑕疵的图像进行校正，得到单元方正的图像.

步骤2：对校正后的有瑕疵图像做低秩分解.

步骤3：以模板TM 作为黄金图像，对低秩分解后的有瑕疵的图像使用GIS 方法，并将大于阈值T的部分标记为瑕疵.

3 实验结果及分析

实验使用香港大学工业自动化实验室提供的纺织品图像样本库.该样本库包含箱形和星形两种图案的无瑕疵及有瑕疵的纺织品图像，其中箱形有瑕疵纺织品包括断端和粗线条两种瑕疵类型的图像，星形有瑕疵纺织品包括粗线条和细线条两种瑕疵类型的图像，并且样本库中同时包括所有有瑕疵图像的基准图（Ground-Truth）.所有图像的尺寸均为256×256 像素，其中无瑕图和瑕疵图为24 位真彩色图像；而基准图为二值图像，1 代表瑕疵部分，0 代表背景.用于对比的方法有BB，RB，ER，WGIS 和TC.用于评价的标准包括真阳性率（查全率）TPR、假阳性率FPR、阳性预测值（查准率）PPV、阴性预测值NPV、检测的准确率ACC.计算式如下：

其中，TP表示算法检测出的瑕疵与基准图中标定的瑕疵一致的部分，FP表示基准图中标定的瑕疵但算法未检测到的部分，TN表示算法检测为无瑕与基准图中标定的无瑕一致的部分，FN表示基准图中标定为无瑕但算法检测为有瑕疵的部分.

由于TN的数值通常比TP大一个量级，相加之后与TN数值相近.为了更准确地评价检测结果，本文同时使用f值的评价方法.f值为查全率和查准率的加权平均值，定义为：

其中，α为权重，当α＞1 时表示查准率占比更重，当α＜1 时表示查全率占比更重.本文将α设置为1，f值越接近1 表示检测结果越好.以f值为评价标准的方法综合考虑了查全率与查准率，同时避免了数据数量级相差较大时，代数和与较大数值接近的问题.

3.1 不同图像插值方法实验结果及分析在图像校正时，为了减小信息丢失的影响，本文使用图像插值的方法，先将图像扩大，并在校正变换之后再恢复为原图的尺寸.而不同的图像插值方法，对于校正之后的检测结果有不同程度的影响.本文针对这一问题进行对比实验，并选择最优的图像插值方法用于图像校正时的处理.

分析表1（表中黑体字为同一类型图像下同一指标的最优值）、图5 和图6 的检测结果，在箱形图案的瑕疵图像中使用箱型插值扩大图像的检测效果最理想，ACC和f值均在较高的水平.最近邻插值方法的查准率最高，但查全率较低；双线性插值方法的查全率最高，但查准率较低.因此在本文后续实验中选用箱型插值来对箱形瑕疵图像进行插值处理.

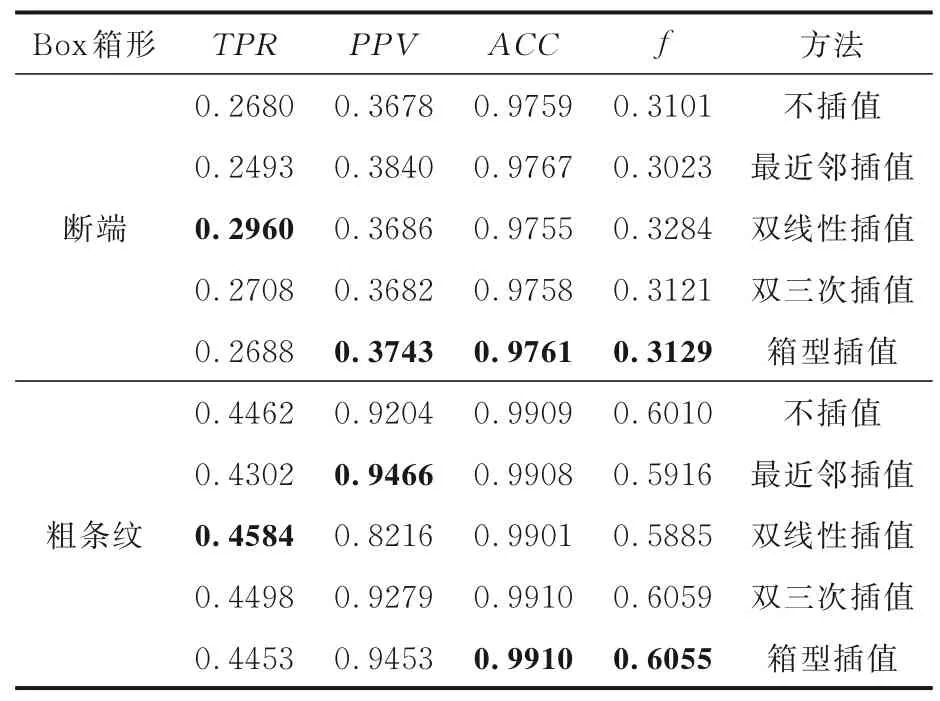
表1 不同插值方法对箱形图案的检测结果Table 1 Detection results of box pattern by different interpolation methods

分析表2（表中黑体字为同一类型图像下同一指标的最优值）、图7 和图8 的检测结果，在星形图案的瑕疵图像中使用双线性插值扩大图像的检测效果最出色.双线性插值方法的查全率有较高的水准，且领先其他方法较多，虽然查准率较低但差距不大.最终计算ACC和f值，双线性插值方法皆为最高.因此在本文实验中选用双线性插值方法对星形瑕疵图像进行插值处理.

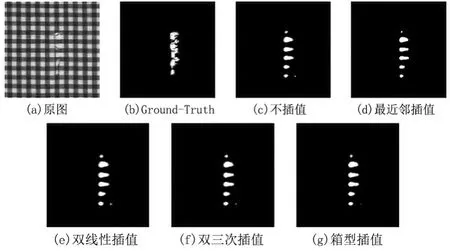
图5 不同插值方法对箱形断端类型瑕疵图检测结果Fig.5 Detection results of box broken end defect image by different interpolation methods

图6 不同插值方法对箱形粗条纹类型瑕疵图检测结果Fig.6 Detection results of box thick bar defect image by different interpolation methods

表2 不同插值方法对星形图案的检测结果Table 2 Detection results of star pattern by different interpolation methods

3.2 本文方法与其他方法的对比实验结果及分析 在箱形图和星形图的样本库中，本文方法与BB，RB，ER，WGIS和TC五种方法进行对比实验.

3.2.1 箱形图分析表3、表4（表中黑体字为同一张图像下同一指标的最优值）及图9 至图12 的检测结果，本文方法在箱形断端类型和粗条纹类型的瑕疵图的检测中效果较好.

图7 不同插值方法对星形粗条纹类型瑕疵图检测结果Fig.7 Detection results of star thick bar defect image by different interpolation methods

图8 不同插值方法对星形细条纹类型瑕疵图检测结果Fig.8 Detection results of star thin bar defect image by different interpolation methods

在箱形断端类型中本文方法表现较稳定，查准率和ACC一直有较高的水平.在两张不同的断端类型瑕疵图的检测中，ER 和TC 都是一张结果较好一张结果较差，甚至在图9 的检测中，ER出现了未能准确地识别出瑕疵的情况.

在箱形粗线条类型中本文方法的查准率和ACC均为最高，且值在图11 中排第一，图12 中排第二，也是有较高的水准.

图13 为不同方法对箱形瑕疵图检测结果的TPR-PPV散点图，越靠近图像的右上角则表示该方法的检测效果越好.本文方法处于偏上端的位置，表明PPV值，即查准率较高；TPR值则处于中间的位置，整体而言更靠近右上角.相较而言，TC 方法处于偏右端的位置，表明TPR值，即查全率更高.其余方法中，ER 虽然有两个点表现较好，但其他两点差距较大，体现出其稳定性较差的特点；WGIS 的查准率较低，并且也有对于不同瑕疵类型稳定性不高的表现；BB 和RB 则靠近图像的左下角，整体表现较差.综合来看，本文方法优于其他五种方法.

表3 不同方法对箱形断端瑕疵图的检测结果Table 3 Detection results of box break end images by different algorithms

表4 不同方法对箱形粗线条瑕疵图的检测结果Table 4 Detection results of box thick bar images by different algorithms

图9 不同方法对箱形断端类型瑕疵图1 检测结果Fig.9 Detection results of box break end defect image 1 by different algorithms

图10 不同方法对箱形断端类型瑕疵图2 检测结果Fig.10 Detection results of box break end defect image 2 by different algorithms

图11 不同方法对箱形粗线条类型瑕疵图1 检测结果Fig.11 Detection results of box thick bar defect image 1 by different algorithms

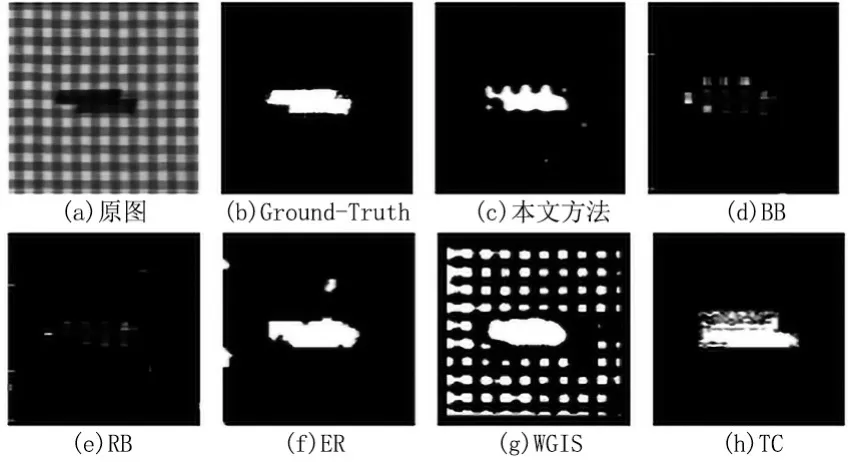
图12 不同方法对箱形粗线条类型瑕疵图2 检测结果Fig.12 Detection results of box thick bar defect image 2 by different algorithms

3.2.2 星形图分析表5、表6（表中黑体字为同一张图像下同一指标的最优值）及图14 至图17 的检测结果，本文方法在星形粗线条类型和细线条类型的瑕疵图的检测中表现较好.

在星形粗线条类型中本文方法的查准率较好，ACC和f值也有较高的水平，在图14 中表现最好，在图15 中处于第三位.在图14 的检测中，在BB 和RB 未能准确识别出瑕疵的情况下，本文方法依然有很好的表现.在图15 中ER 则表现出了更高的水准.

图13 不同方法对箱形瑕疵图检测结果的TPR-PPV 散点图Fig.13 TPR-PPV scatter plots of different algorithms on box images

表5 不同方法对星形粗线条瑕疵图的检测结果Table 5 Detection results of star thick bar images by different algorithms

在星形细线条类型中本文方法查准率和查全率有较高的水平，ACC和f值处于领先位置.TC在检测中的查准率体现出高水准，本文方法在ER和BB 分别未能准确识别瑕疵的情况下也保持了较好的结果.

图18 为不同方法对星形瑕疵图检测结果的TPR-PPV散点图.本文方法整体处于中间上部的位置，在PPV值，即查准率上有较大的优势；TPR值则位于中间部分，较为稳定.TC 方法的TPR值，即查全率处于领先的水平，因此更靠近图像的右端，整体来说在准确度上与本文方法相近.在其余方法中，ER 和WGIS 的分布范围较大，稳定性较差，且在两项数据中没有突出的优势；BB 和RB 则集中在图像的左下角，表现出的检测结果较差.综合来看，本文方法优于其他五种方法.

表6 不同方法对星形细线条瑕疵图的检测结果Table 6 Detection results of star thin bar images by different algorithms

图14 不同方法对星形粗线条类型瑕疵图1 检测结果Fig.14 Detection results of star thick bar defect image 1 by different algorithms

图15 不同方法对星形粗线条类型瑕疵图2 检测结果Fig.15 Detection results of star thick bar defect image 2 by different algorithms

图16 不同方法对星形细线条类型瑕疵图1 检测结果Fig.16 Detection results of star thin bar defect image 1 by different algorithms

图17 不同方法对星形细线条类型瑕疵图2 检测结果Fig.17 Detection results of star thin bar defect image 2 by different algorithms

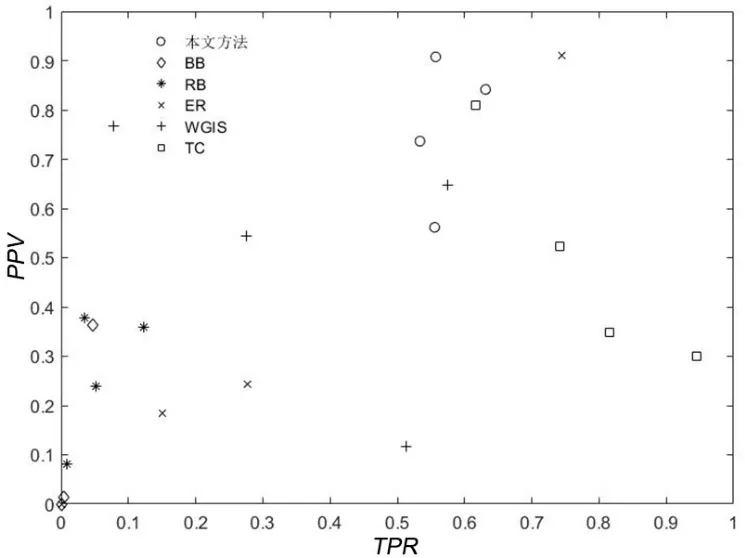
图18 不同方法对星形瑕疵图检测结果的TPR-PPV 散点图Fig.18 TPR-PPV scatter plots of different algorithms on star images

4 结论

本文提出一种基于图像校正和模板匹配的纺织品瑕疵检测方法.针对具有周期性图案的纺织品的瑕疵检测问题，使用基于Hough 变换和透视变换的图像校正方法，有效解决了原始图像图案的不规则导致的图像间模板差异较大的问题；进一步通过周期计算自适应分割和模板校正的方法进行模板选取，将图像进行低秩分解后，使用GIS方法标记出纺织品的瑕疵部分.由实验结果可知，本文方法对于箱形图的两种瑕疵类型和星形图的两种瑕疵类型都有较好的检测效果.该方法的局限性在于模板的使用导致较小和较不明显的瑕疵不能准确地识别，未来将针对上述问题进行深入研究，寻找解决方案.