结合时间遗忘和项目流行度的协同过滤推荐算法

赖国传 刘广聪

（广东工业大学计算机学院 广东省广州市 510006）

随着互联网的快速发展，尤其是5G 的逐渐普及，互联网上的资源呈现爆炸式的增长，造成了“信息过载”的问题，即用户难以从海量的信息中寻找到所需、有用的信息。推荐系统应运而生。

推荐系统是帮助用户有效地发掘有关信息的一种工具，它不需要用户提供清晰的需求，而是通过对用户历史行为进行分析，以满足用户需要和兴趣。一方面，推荐系统能帮助用户在大量的互联网信息中寻找自己所感兴趣、有用的信息，另一方面，也能帮助信息提供商，使信息提供者的信息更多地受到用户关注，从而实现了用户与服务商双赢的目标。

协同过滤推荐算法以其优异的性能迅速发展。协同过滤推荐只关注用户或项目之间的关系，而不需要关注用户或项目本身的内容，因此具有很强的适应性，可以产生新的、不同的推荐和个性化推荐。然而，由于其广泛的应用，其系统暴露出冷启动、稀疏性和低可扩展性等缺陷。当用户和项目数量迅速增加时，用户项目矩阵会非常稀疏，这会降低计算的准确性，增加系统的计算时间，导致系统无法实时推荐，影响推荐效率。

1 相关工作

1.1 基于用户的协同过滤推荐算法

基于用户的协同过滤推荐算法的基本思想是通过用户评分数据，找到目标用户的相似用户，根据相似用户的已有行为的项目进行推荐。这种推荐的本质是为目标用户推荐与他相似用户喜欢的项目。

其基本步骤如下：

（1）由用户集U={u1, u2,……,un}以及项目集I={i1, i2,……,im}两个集合构建用户-项目评分数据矩阵R。表1 给出了用户项目评分矩阵的例子。其中的数值表示用户u 对项目i 的具体评分，0 表示未评分。

（2）根据上述用户项目评分矩阵，计算用户-项目相似性sim(i,j)；

（3）依据第二步得到的用户间的相似性，筛选出目标用户u的邻居用户，组成邻居集Nu；

（4）得到目标用户的邻居集后，借助邻居集内用户的评分数据来预测目标用户对项目的评分Pu,i。常用的评分公式如下：

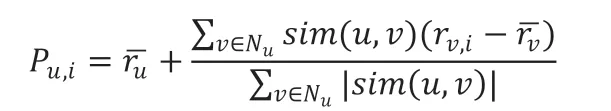
表1：用户项目评分矩阵

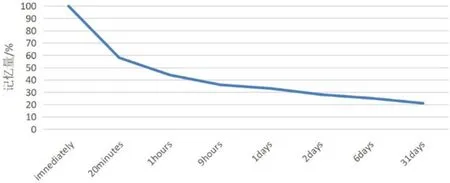
图1：艾宾浩斯遗忘曲线

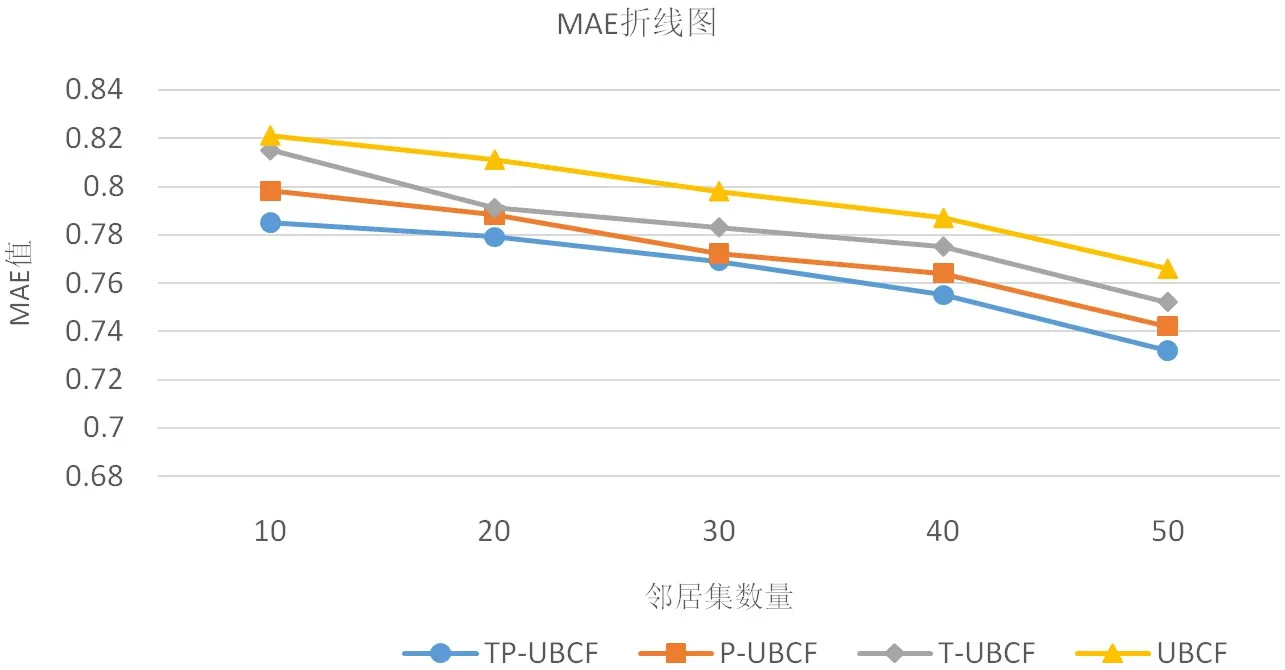
图2

1.2 相似度度量方法

传统的协同过滤推荐算法中，用户-项目相似性的计算公式通常有三种，分别是余弦相似性、改进的余弦相似性和皮尔逊相似性。

这里采用皮尔逊相似度公式来度量用户之间的相似性，其表达式为：

2 结合时间遗忘和项目流行度的协同过滤推荐算法

2.1 艾宾浩斯遗忘规律

德国心理学家艾宾浩斯（H.Ebbinghaus）的一项研究结果发现，在开始学习后立刻就会开始遗忘记忆，而且这种遗忘记忆过程并非完全线性。最初遗忘的时候速度应该是很快的，然后逐渐变慢。他本人认为，"保持和遗忘是时间的函数"。他用无意义音节（由若干音节字母组成、能够读出、但无内容意义即不是词的音节）作记忆材料，用节省法计算保持和遗忘的数量。并根据他的实验结果绘成描述遗忘进程的曲线，即著名的艾宾浩斯记忆遗忘曲线。其中，坐标横轴为时间，竖轴则表示仍然保持记忆的内容量，艾宾浩斯遗忘曲线如图1所示。

2.2 时间函数

人的记忆量随时间的推移而变化，用户的爱好也同样随着时间的推移发生了变化，但传统的协同过滤推荐算法没有把这种用户的爱好列入其考虑范围。因此，针对用户的兴趣转移问题，本文使用的方法是引入艾宾浩斯遗忘曲线为时间函数，赋值用户评分的数据，使其更符合记忆忘却规律。通过拟合上述艾宾浩斯的遗忘曲线，得到了函数的拟合表达式：

f(x)=31.8*x-0.125(x>0)

其中，表示用户评论至现在记忆的保留率，其值越大表明记忆的保留率越高。x 表示从评论到现在的时间。对函数值进行标准化，有：

f(t)=0.3511*(t-t0)-0.125

其中，t0表示用户上一次评分的时间。也就是说，距离上一次评分的时间越久，用户兴趣可能发生变化的可能性也就越大。

2.3 项目流行度偏差问题

项目的流行程度一般是指用户对项目进行评分时的次数，反映了该项目的热门程度。通常情况下，热门项目更易引起人们的关注，被用户知道后，就会变得更热门，而冷门项目则相反。这就是流行程度偏差的现象。传统协同过滤推荐算法一般存在流行偏差现象，即流行程度越大，越频繁地被推荐，而流行程度越低的项目就不容易被推荐给用户，从而使用户更多接受流行程度较高的项目，从而减少了接受流行程度较低的项目。这与推荐系统的多样化和新颖性不符。因此，为了缓解流行偏差现象，需要适当减少高流行程度的项目被推荐的机会，而让流行度低的项目被正常的推荐。

2.4 项目流行度

传统的协同过滤推荐算法通常忽略了项目流行度的影响，导致了流行度高的项目常被过度的推荐，但却不是用户真正所需要的商品。为了缓解这种现象，需要在目标用户进行预打分时加入项目流行度惩罚因子θ，以降低流行度较高的项目所占权重。首先，对项目流行度进行归一化，得到项目标准流行度ps，ps取值在[0,1]区间内：

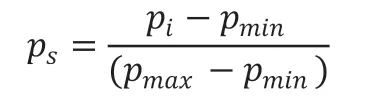
对其进行适当缩放，以避免项目流行度对推荐产生过度影响，得到项目流行度加权惩罚因子θ，

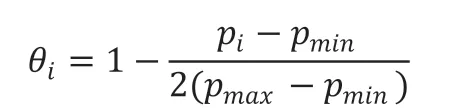
其中，pi代表项目i 的流行度，以项目所获评价次数作为衡量项目流行度的标准，即pi表示项目i 在所有用户中获得评分的次数，pmax是所有项目中流行度的最大值，pmin为最小值。因此，项目流行度越高，pi值越大，越应该受到抑制，所占的权重也就越低，反之亦然。

2.5 算法描述

输入：用户-项目评分表

输出：推荐项目列表

（1）构造改善用户兴趣迁移问题的时间函数，通过时间函数计算得到符合用户记忆遗忘规律的用户-项目评分矩阵Rt；

（2）计算所有项目流行度，组成项目流行度权重集合；

（3）利用皮尔逊相似度计算公式对Rt进行运算，获得用户间相似性结果；

（4）根据Top-N 原则挑选出目标用户的N 个最近邻居，形成邻居集；

（5）借助邻居集以及项目流行度权重集合预估目标用户评分，获取推荐列表。

3 实验结果及分析

3.1 实验数据集

本文采用明尼苏达大学GroupLens 小组发布的MoviesLens100K数据集进行实验。该数据集是一个用户对电影进行评分的数据集，采用五级评分制，评分越高，用户对电影的喜爱程度越高，0 代表无评分，每位用户至少参加了20 部影片的评分。本文从中选取80%的数据作为训练集，剩余20%作为测试集。

3.2 算法评估指标

不同的评价指标反映的是算法在不同层面上的性能。平均绝对误差MAE 是评价推荐系统最常见的指标，它是用来描述预测值和真实值之间的误差。MAE 值的大小与推荐算法的准确度成反比，即MAE 值越小，表示推荐越准确，推荐算法的质量就越好。

MAE 的计算公式如下：

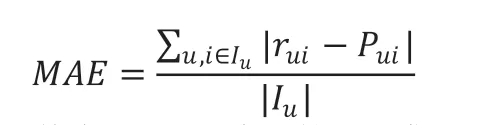
其中，Iu是用户u 的评分集；rui是用户u 对项目i 的真实评分值；Pui是用户u 对项目i 的预测评分值。MAE 值越小，表示预测准确度越高。

3.3 实验结果

为了验证本文所提出的改进算法TP-UBCF，邻居集的数量设置在一定范围内，通过比较不同邻居集数量下的MAE 值做了多组实验。其中邻居集数量的取值分别为10、20、30、40、50.对比算法包括传统基于用户的协同过滤推荐算法（UBCF）、仅基于时间遗忘的协同过滤推荐算法（T-UBCF）、仅基于项目流行度的协同过滤推荐算法（T-UBCF），所有算法均在相同的环境下实验，采用相同的用户评分预测方法。

MAE 对比实验如图2所示。实验结果表明，四种推荐算法的预测准确度都在10 至50 的邻居集数量区间范围内随着邻居集数量的增加而增加，均在邻居集数量为50 时达到最高。本文提出的基于时间遗忘和项目流行度的协同过滤推荐算法在全区间范围内的预测准确度均高于其他三种算法，由此表明本文提出的改进算法TPUBCF 具有更好的性能。

4 结束语

本文提出了一种基于时间遗忘和项目流行度的协同过滤推荐算法TP-UBCF。其中，为缓解用户兴趣漂移的问题，通过引入时间函数，对用户评分进行权重赋值，使时间越远的评分产生的影响越小，从而改善了用户兴趣迁移的问题，提高了推荐的准确度；针对项目流行度偏差的问题，通过对流行度高的项目进行降权惩罚，增加了其他流行度低的项目被推荐的可能性，从而使推荐系统的多样性和新颖性得到有效提高。实验结果显示，TP-UBCF 在一定程度上能提高预测的准确度，由此证明TP-UBCF 改进是有效的。