基于MATLAB的感应加热模型的仿真与研究

李城磊 张瑞平

（山西大同大学机电工程学院 山西省大同市 037003）

国内外孔轴配合件的拆卸方法中，采用温差法的工艺主要有火焰加热法、油浴加热法、物理制冷法、感应加热法等。感应加热方法因其速度快、功率消耗小、温度易于控制，可以实现孔轴类零件节能、安全、无损、高效的原则，但感应加热中包括对温度的控制、频率的调节等对电磁场参数的设计具有一定的影响，其模型的搭建有利于感应加热实验的进行[1]。

1 感应加热原理

感应加热的工作原理：向多匝线圈通入交变电流，此时线圈中就会产生交变磁通，在磁场的作用下，使得感应圈中的金属材料产生涡流[2]，从而工件内部产生热量，以此来实现实验的目的。

2 电磁场计算模型

2.1 电磁场基本定律

电磁感应加热的整个过程通过以下几个基本定律来加以叙述，其中包括安培环路电律、法拉第电磁感应电律、高斯电通定律、高斯磁通定律。

安培环路定律：磁场强度通过闭合路径的积分，等于穿过此闭合路径形成曲面的电流的代数和。

积分形式

式中：

矢量（C/m2）

S-闭合曲面 的界限。

法拉第电磁感应定律：导体回路中的感应电动势与穿过此路径的磁通量随时间的变化率成正比。

积分形式

式中：

高斯电通定律：介质中穿过任一闭合曲面的电位移矢量D 的通量等于该闭合面包围的电荷量。

积分形式

式中：

ρ-电荷体密度（C/m3）

V-闭合曲面S 围成的体积区域。

高斯磁通定律：传出一个闭合路径的磁通量恒等于0，这里的磁通量指的是磁感应强度矢量对闭合路径的有向积分。

积分形式

2.2 涡流集肤效应

根据麦克斯韦方程组以及相应的基本方程式可以推导出：

磁场强度随时间变化的谐波方程为：

考虑到磁场强度分布的一维对称性，取柱坐标，有：

由电磁场基本方程组的复数形式及辅助方程式可得：

由式（8）及基本方程组的复数形式可得：

根据式（5）及（9）得：

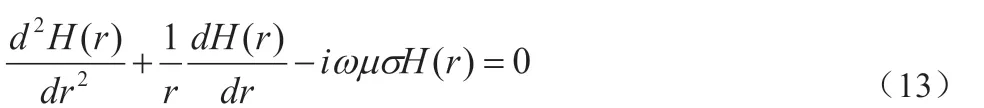
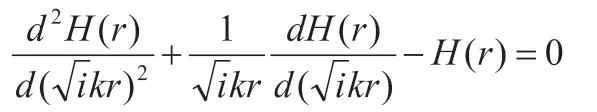
方程通解为：

根据上式，从而得到了导体内部磁场的分布情况为：

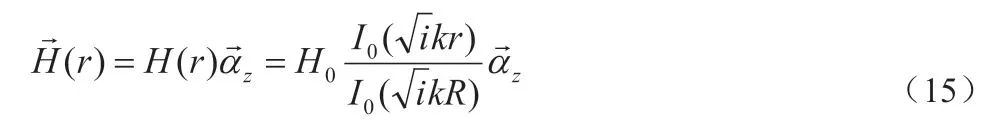
图1：低频状态集肤深度与电源频率曲线

图2：中频状态集肤深度与电源频率曲线

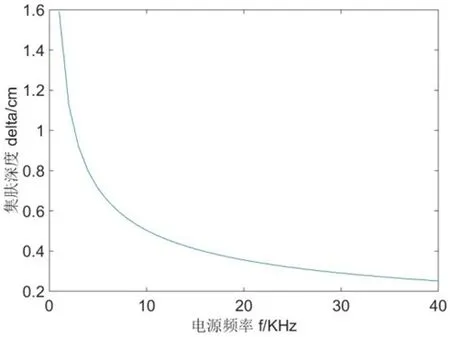
图3：高频状态集肤深度与电源频率曲线

表1：45 号钢的物性参数[5]

表2：电磁场和涡流分布的计算机仿真曲线

由电磁场基本方程组的复数形式得：

其中Bessel 函数的递推公式：

将式(12）代入（13）得：

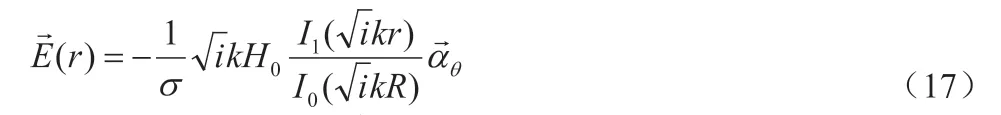
因此电场强度和涡流密度分布为：

3 MATLAB模拟实验

本文主要是通过MATLAB 软件，以感应加热过程中电磁场参数进行设计，对其进行数值模拟和仿真。

涡电流的集肤深度公式如下所示：

式中：

δ—涡电流的集肤深度（cm）

ρ—材料的电阻率（Ω·cm）

f—通电电流的频率（Hz）

μ—被加热工件的相对磁导率

电磁场中参数如下：

图4

计算过程如下：

（1）当处于低频状态（f=0-50Hz）时，MATLAB 仿真曲线如图1所示。

（2）当处于中频状态（f=1-10kHz）时，MATLAB 仿真曲线如图2所示。

（3）当处于高频状态（f=0-40kHz）时，MATLAB 仿真曲线如图3所示。

从MATLAB 仿真曲线中可以看出，当被加热工件的电阻率ρ、磁导率μ 为确定值时，集肤深度取决于被加热工件的频率f，频率越高，集肤深度越浅，集肤效应也就越明显，从而对集肤效应有清晰直观的了解[3]。

表1 和表2 是用MATLAB 软件对被加热工件电磁场和涡流密度分布曲线进行仿真。

推导过程如下：

根据以上参数，编制MATLAB 仿真程序如下：

U1=186.6;

U0=4*pi*(1e-9);

u=u1*u0;

sigema=2.949*1e6;

f0=3000;

w0=2*pi*f0;

k0=sqrt(w0*u*sigema);

f1=10000;

w1=2*pi*f1;

k1=sqrt(w1*u*sigema);

f2=20000;

w2=2*pi*f2;

k2=sqrt(w2*u*sigema);

R=0.1;

r=0.065:0.01:0.1;

semilogy(r/0.001,abs(besseli(0,sqrt(i)*k0*r))/abs(besseli(0,sqrt(i)*k0*R)),...

r/0.001,abs(besseli(0,sqrt(i)*k1*r))/abs(besseli(0,sqrt(i)*k1*R)),...

r/0.001,abs(besseli(0,sqrt(i)*k2*r))/abs(besseli(0,sqrt(i)*k2*R)));

xlim([65,100])

set(gca,'XScale','linear','YScale','log');

title('感应加热工件内电磁场及涡流密度曲线');

xlabel('工作半径f/mm','fontsize',10)

ylabel('|E/E0|、|J/J0|','fontsize',10)

grid on

根据以上参数用MATLAB 软件进行仿真曲线的绘制，分布曲线图如图4所示。

从MATLAB 电磁场及涡流密度仿真曲线可以看出，在感应加热的过程中，越靠近被加热工件的表面，涡流产生的热量将会越来越多，而且电磁场和涡流密度的集肤效应愈发明显，|E/E0|、|H/H0|、|J/J0|变化规律均一致[4]。

4 结论

本文以电磁感应理论为基础，利用MATLAB 仿真曲线和仿真实验数据相结合的方法，对被加热工件进行仿真研究，建立在不同频率下的集肤效应曲线，该仿真实验在感应加热的模拟、设计为研究人员提供了一些参考[5]。

被加热工件在感应加热过程中，在温度为200 摄氏度，线圈内径在200mm 以内，频率在3-40KHz 的范围内所建立的集肤效应曲线符合生产实际所需，该模型也为感应加热模型的分析、设计提供了一些新的思路和研究方法。