基于“类”架构的数学教学探索
陈莉
【摘 要】在小学数学教学过程中,有很多零散的知识点,在一定程度上会影响学生的理解、记忆和掌握,因此,在实际教学中,教师要能从整体视角去设计教学,把一个个相关的知识点有序地、有规律地串联起来,从而让学生更好地去理解数学本质。基于“类”架构的数学教学主要包括“类知识”和“类方法”,本文将围绕这两方面进行阐述。
【关键字】“类知识” “类方法” 整体视角 整体规划
“常州市中小学学科教学建议”小学数学部分指出:在小学数学课程在实施过程中,应打破零散的知识观,建构课程整体观。通过知识结构体系视角建构学生数学学习,主动把一堂堂课串联成有结构、有系列、有思想的数学课堂,整体设计一周、一月甚至一个学段的数学课的教学目标,形成基于“类”架构的课堂教学整体规划。在实际教学中,如果教师能从整体视角设计教学,不仅能体现数学的本质,使学生理解数学知识中所蕴含的思想方法,而且能引领学生经历数学知识的探索过程,获得积极的情感体验,下面笔者就围绕“类”教学谈谈自己的看法。
一、“类知识”
所谓“类知识”是指表面看似关系不大,但是实际存在一定联系的数学知识进行归类教学。
(一)关注本质,使数学知识系统化
某些数学知识从表面上看联系不大,但是如果关注其本质,存在着紧密的联系。例如,“小数的意义”这部分内容,其形式与整数和分数截然不同,但是其本质和整数的意义和分数的意义还是有很多的共同点的,当然也有其特定的含义。小数意义的理解关键在于小数部分的单位的建立与位值的理解,如果能与整数的十进制记数法等知识进行恰当的联系,那么学生对小数的认识就不再是一个独立的个体,而是一个相对整合的系列化过程。例如,苏教版数学“小数的意义和性质”是五年级上册的内容,教材中例1呈现:1分米等于几分之几米?写成小数是多少米?3分米呢?实际上在这里就蕴含着小数与整数之间的联系,即“把一个比较小的数量用大单位来表示,就是小数”。同一个数量,用小单位表示就是整数,用大单位表示就是小数。在教学这部分内容时,重点是基于学生对原有的小数初步认识的基础上的,利用小数与整数在计数制上的共同之处,着重使学生理解小数部分的单位建立与位值,把小数的认识与整数的认识建立起联系,由对小数的初步的直观认识,扩展到对小数意义的理解,并将小数的意义用于具体的数量的解释。从而将整数、小数的内在联系有机统一起来,形成一个相对完整的“数”认识。
(二)对比异同,使数学知识模块化
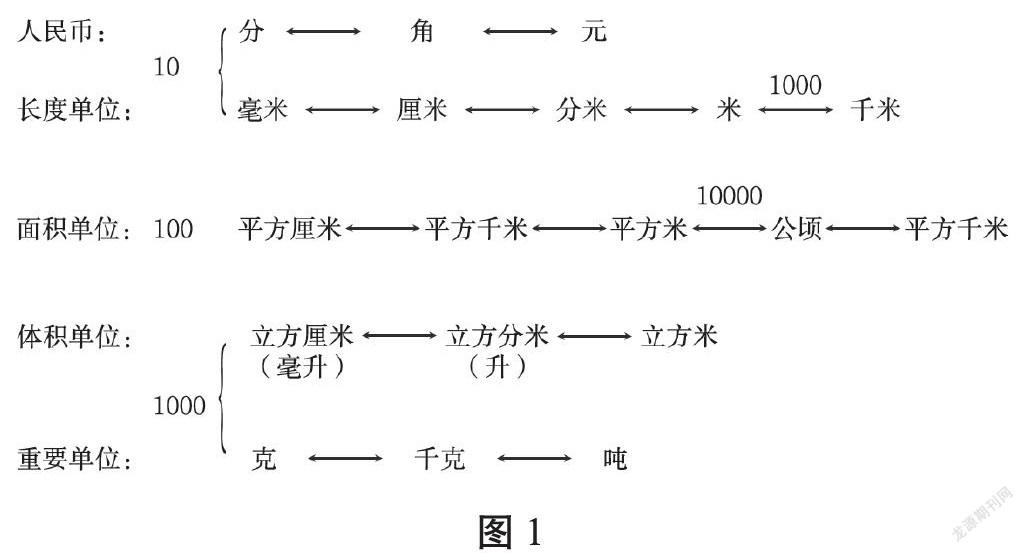
单位之间的进率换算多而杂,学生很容易混淆,各种错误层出不穷,如果就“题”论“题”,学生几乎没什么概念,该错还是错,但是如果能把一些常见的进率关系进行整理和比较,形成简洁明了的结构图,那么学生的认知结构就会变得清晰而有条理,提取的时候就会更加准确。笔者设计了进率结构图(见图1)。
通过这张结构图,笔者把相邻两个单位进率为10、100、1000的分别进行分类,并用不同颜色的笔标注出来,帮助学生理解。将这些琐碎易混淆的进率知识模块化,还可以减轻学生的记忆负担,提高记忆效果。
(三)融合视野,使数学知识整体化
苏教版数学教材主要采用“分步实现、螺旋上升”的原则编排教学内容,虽然满足了不同发展阶段学生的课程需求,但是客观上也造成了同一知识的过度分散。这样的安排让学生很难明白所学的知识点在整个单元、整册教材乃至整个教材体系中的地位和作用,这將不利于学生对知识的提取和自身能力的提升。这就要求我们整体、有序地把握教材体系,把每堂课的教学目标放到整个教学体系中来设定,使得课时目标和长程目标有机统一。如苏教版数学四年级上册“数的改写”中,要求学生掌握将整万数、整亿数改写成以万、亿作单位的数,将非整万数、整亿数改写成以万、亿作计数单位的近似数;在五年级上册,要求学生掌握把较大的非整万数、整亿数改写成用“万”或者“亿”做单位的近似数。在苏教版数学七年级上册,在教学“近似数”这部分内容时,教师先教学了有关乘方的知识,在此基础上引出有效数字,如3.30×104精确到哪一位,有几个有效数字?如何确保第二学段与第三学段的整体融通性,在第二学段第一次数的改写学习时应增加“以十、百、千作计数单位的数的改写”,如将45678分别改写成以十、百、千、万作计数单位的数。让学生理解数的改写是将“个”的计数单位改写成其他计数单位,只要将计数单位后面一位上的数四舍五入后加上计数单位。这样便于学生在第二次学习时理解数的改写就是去掉计数单位后面的0,也相当于将个位后面的小数点向左移动到相应的位置,而保留相应的小数数位相当于第三学段将要学习的科学计数法以及有效数字的相关内容。例如,将45678改写成以万作单位的数是4.5678万,如果改写成以百作计数单位的近似数,则相当于将结果保留两位小数就是4.57万,第三学段则表示为4.57×104 ≈4.57×104,取3个有效数字。
二、“类方法”
“类方法”是指把一些看似无关的问题,转化成同一种方法或类似的方法去解决。
(一)拓展体验——“类方法”赋予数学思想更宽阔的提升力
数学基本思想是数学精神的核心部分,它可以让我们保持一种开阔的视野,用更理性的大脑去看待问题、关注周遭、理解世界。一些看似无关的问题可以通过数学思想这一内隐线索有机串联起来,让问题变得更简洁、更清晰。例如,在苏教版数学三年级上册“找规律”中提到:两个物体“一一间隔排列”有三种情形,那就是“两端物体相同”“两端物体不同”“围成封闭图形”。大部分教师会把它分为三种类型来教学,过于强调三种类型的特征与对应的解题模型,但是学生并不领情,这种机械无关联的记忆对于学生来说很难内化。其实不管哪种类型,如果用“一一对应”的思想去思考,两种数量的关系都会变得一目了然。并且采用“一一对应的思想”的基本模式还可以解决适当变化的各种新问题,如植树问题、路灯问题、楼梯问题、锯树问题、排队问题等。
(二)关联思考——“类方法”赋予解决问题更强大的生长力
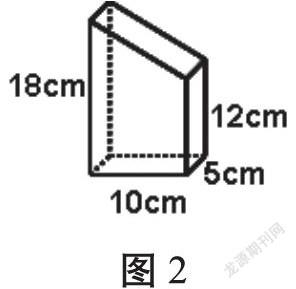
数学问题千变万化,当面对一个新问题束手无策时,最好的办法就是联想与此相关的解决问题的方法,由此及彼,找到解决新问题的突破口。如在解决如下问题时(见图2)。
将一块长方体木条,锯成立体小木块,求小木块的体积是__________cm3。
学生刚接触这个问题时,会觉得无从下手,但是进行关联性思考后会发现,在求梯形面积时,是把两个完全相同的梯形拼成一个长方形,通过先求长方形面积再求出梯形面积,那么,求类似的梯形的体积时是否也可以考虑把两个完全一样的立体图拼起来的方法,果然,这是解决这个问题最简洁的方法。
(三)类比结构——“类方法”赋予数学思维更完善的整合力
苏教版数学教材中的很多相关内容在编排时,结构类似。如长度、面积、体积这三块内容,均属于度量单位,虽然教材所处的学段不同、内容不同,但是在学习的过程中,都要经历以下几个步骤:(1)体会统一度量单位的必要性;(2)认识度量单位;(3)建立表象;(4)判断单位是否适宜;(5)用单位度量;(6)进行单位换算。在对度量单位的学习和认识过程中,学生必将经历从非标准单位到标准单位的过渡,认识度量单位,体会单位的重要性,并在各项活动中初步感受度量单位的特性。在学习长度单位的时候,教师要引导学生回顾学习的步骤;在进行面积单位教学的时候,教师要把学习的步骤和长度单位学习的步骤进行类比,体会教材编写的价值,从而引导学生更好地学习体积单位,同时,从整体上把握学习度量单位的方法和它们之间的内在联系。
总之,教师只有引导学生从整体视角出发,用“类知识”“类方法”的眼光去看待数学问题,学生们才能更好地理解数学的本质和内涵。

