含吸声层和阻尼层叠层板的动力学建模研究
陆 静,王 青,陈 莎,王宇翔
(1. 广西科技大学 机械与交通工程学院,广西 柳州 545006;2.广西汽车零部件与整车技术重点实验室,广西 柳州 545006)
多孔介质材料可以高效可靠地控制结构的噪声,而阻尼材料具有良好的减振性能,因此,同时敷设多孔介质材料和黏弹性阻尼材料的复合结构可以有效提高结构的抗振性、稳定性,并大幅降低结构噪声,减振降噪的效果非常显著。另一方面,含吸声层和阻尼层的叠层结构还具有简单可靠、价格低廉等特点,因此,此类复合结构在工程中有广泛的应用。但是,现有文献的研究对象多是仅含多孔介质材料或仅含黏弹性材料的简单叠层结构,对于同时敷设多孔介质材料和黏弹性阻尼材料复合板的研究较少。目前,分析层合板动力学特性常用的方法为解析法、有限元法和半数值半解析方法。1994年,Theodorakopoulos等[1]采用傅里叶级数展开的方式求解了四边形简支多孔介质薄板的弯曲振动问题。Kerwin[2]首次建立了含黏弹性阻尼材料普通夹芯板的动力学方程,但是该理论仅在黏弹性阻尼材料的阻尼系数较小并且约束层厚度较薄时才适用。解析法具有非常高的求解精度和稳定性,但它仅适用于简单规则的结构和特定的边界条件,应用范围很小,有限元法逐渐成为分析层合板的主要手段。Johnson[3]将复合板分为三层夹芯结构,用有限元软件NASTRAN分析了夹层板结构频率和损耗因子。Yamaguchi等[4]通过多孔介质薄板内部流体的三维离散方程得出内部流体的位移表达式,结合骨架的控制方程建立了多孔介质薄板的整体动力学方程,进而建立了叠层多孔介质薄板的有限元近似模型,对含多孔介质叠层板的阻尼振动特性进行了分析。邓年春等[5]基于虚功原理和层合理论,采用四节点板单元构建出一种新型的含黏弹性阻尼层叠层板的复合板单元。刘天雄等[6]充分考虑黏弹性阻尼层纵向位移对整体复合板结构的影响,通过引入虚拟自由度,推导出叠层板的标准二阶常线性系统模型,避免了因黏弹性材料性能属性导致的高阶非线性方程。然而,敷设阻尼层和吸声层后结构趋于复杂,有限元法的处理也更为困难。而且,有限元法的计算精度主要依赖于网格的划分,随着频率的增加,在计算工作量与计算精度控制上都无法得到有效的保证。因此,邹元杰等[7-10]提出了半解析半数值方法。李军强等[11]通过扩充状态变量, 基于精细积分法提出了一种弹性-黏弹性复合结构动力响应的分析方法。唐国金等[12]基于能量原理提出了一种传递函数法,建立约束阻尼层矩形薄板的系统运动方程,对拓展传递矩阵或传递函数法的应用起到了积极的作用。但由于状态向量采用位移及其高阶导数,在应力边界条件时处理较复杂。在此方法的基础上,向宇等[13-14]借助高精度的精细积分法提出一种分析含黏弹性阻尼层叠层结构动力学特性的半数值半解析方法,该方法可以方便地应用于各种边界条件。随后,向宇等[15]又将该方法用于多孔介质薄板动力学特性的分析,该方法充分考虑了流体在三个方向上的位移及其与骨架的耦合作用,具有较高的精度和稳定性。
本文结合经典的薄板理论和三维Biot理论,利用分层理论建立了含吸声层和阻尼层叠层板的整合动力学控制方程,并结合边界条件和齐次扩容精细积分方法提出了一种分析此类叠层板结构动力学特性的半解析半数值方法。该方法的状态向量包含了位移、应力和声学分量,可直接应用多种边界条件,具有较高的计算精度,且由于避免了单元划分,可适用于较高的频率范围。本文的建模方法、求解方法和研究成果可望为此类叠层板的动力学特性研究提供一定的理论基础和技术支撑。
1 含吸声层阻尼层叠层板的动力学建模
为了便于推导,文中采用以下假设:①不计板横向变形,且三层横向位移(挠度) 相同;②各层之间没有滑移,层间位移连续;③基层和约束层采用Kirchhoff 假设;④只考虑黏弹层的剪切效应,忽略其纵向刚度( Kerwin 假设) ;⑤忽略转动惯量的影响。
1.1 基层板控制方程
设基板为一个矩形薄板,其x和y方向长度分别为L和b,y方向的边界条件为两端简支,将物理量进行傅里叶变换并无量纲化后,可导出谐激励作用下基层板的一阶常微分方程为
(1a)
(1b)
(1c)
(1d)
(1e)
(1f)
(1g)
(1h)
式中:上标(1)为基板;ξ=x/L;u,v,w,φx分别为x,y,z三个方向的位移及转角;Nx,Sx,Mx,Vx分别为单位长度上沿x方向的轴力、等效面内剪力、等效横向剪力和弯矩;px,py,pz分别为x,y,z三个方向的载荷,包括外载荷和层间的相互作用力;上标“~”为相应物理量的幅值;上标“—”为相应物理量幅值的无量纲值,系数gij(i,j=1,…,8)的表达式详见文献[16]。
1.2 多孔介质薄板控制方程
采用与1.1节相同的方法,可导出谐激励作用下多孔介质薄板的一阶常微分方程为
(2a)
(2b)
(2c)
(2d)
(2f)
(2g)
(2h)
(2i)
(2j)
(2k)
(2l)
1.3 层间相互作用力
1.3.1 法向相互作用力
基层板、黏弹性阻层、多孔介质层之间的法向受力分析受力图如图1所示。
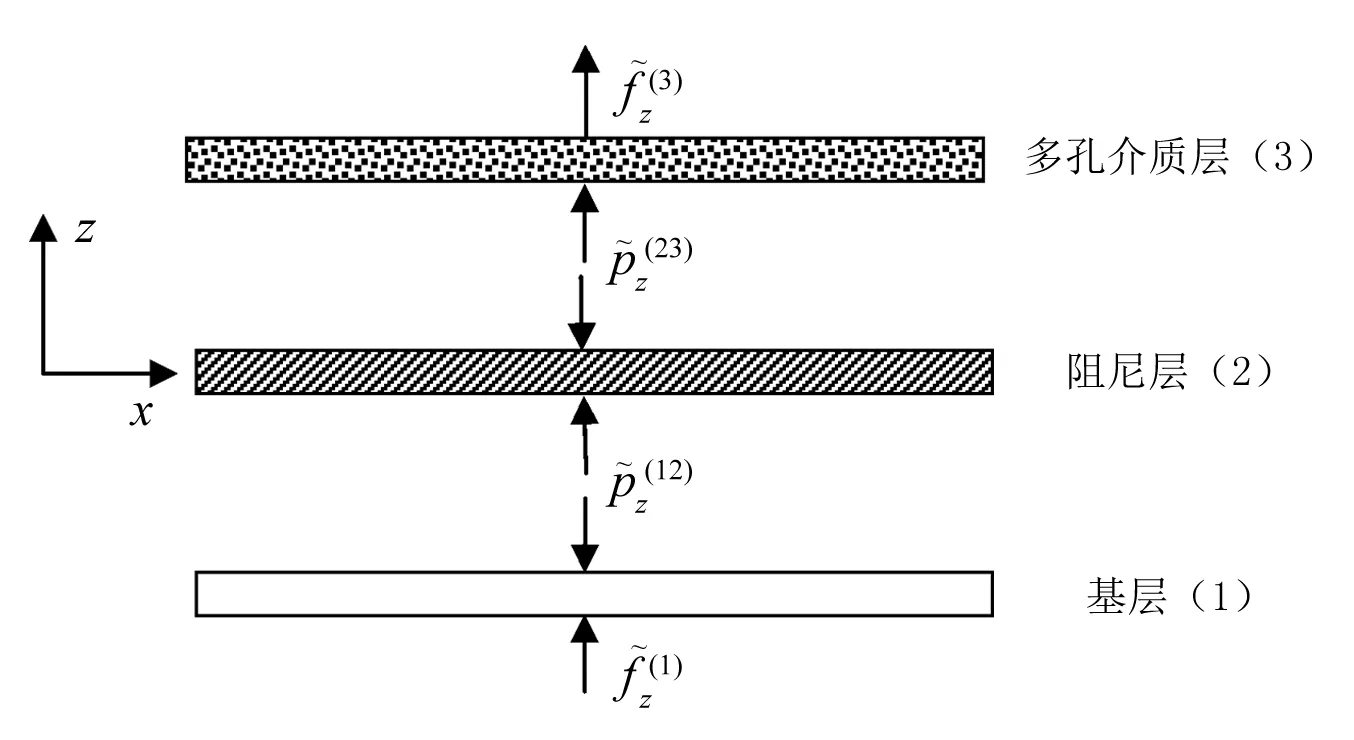
图1 层合板之间的法向相互作用力Fig.1 Interaction normal force between laminates
由图1可以看出,黏弹层法向的受力平衡为
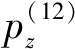
1.3.2 黏弹层的切向力与偏心力矩
对于基层板和多孔介质薄板,由kirchhoff平面假设与薄板理论,可得
(4)
对于黏弹层内任意点的位移,采用一阶剪切形变理论
w(x,y,z)=w(x,y)
(5)
由式(5)可写出黏弹层中面的剪切应变
(6)
由胡克定律和层间的位移连续性条件可求出黏性层内沿x和y方向的剪应力,将其进行无量纲化后可得
(7)
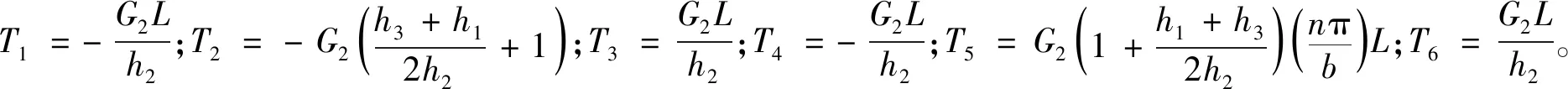
由图2可知,叠层板中的黏性层剪切力对基板和多孔介质板中面所产生的偏心力矩为
(8)
式中,e1,e2分别为黏弹性层中面到基层中面和多孔介质层中面的偏心距,e1=(h1+h2)/2,e3=(h3+h2)/2。
结合式(8),可求出偏心距所产生的z方向等效剪力为
(9)

图2 黏弹性层的剪力Fig.2 Shear force of the viscoelastic layer
1.4 含吸声层阻尼层叠层板控制方程
考虑黏性阻尼层的自重及剪切力作用的影响,式(1)和式(2)中的非齐次载荷可以写为
(10)
结合式(1)~式(3)、式(7)~式(10)可消去层间未知的相互作用力,经整理后可导出叠层板的动力学方程,写成一阶常微分方程的形式为
(11)
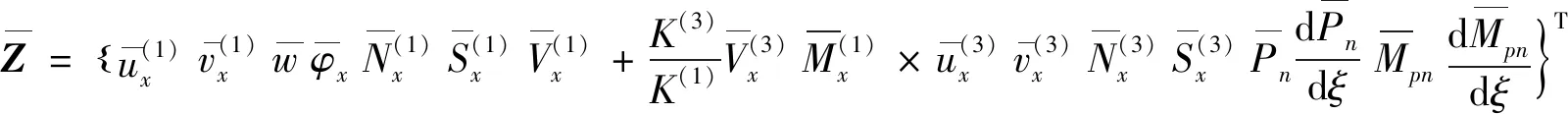
2 求解方法
2.1 边界条件的处理
将叠层板在整个求解域划分为NN个单元,每个单元内通过齐次扩容精细积分法求解式(11),可求出端点处的状态向量,移项整理后可得
-TjZj-1+Zj=Qj
(12)
式中:j=1~NN;Zj,Zj-1为第j个单元的两个节点的状态向量;Tj为传递矩阵;Qj为外激励引起的非齐次项。在整个求解域内可列出NN个类似的矩阵方程。在板的两个边界上各有8个已知的边界条件,将其加入后即可得出16(NN+1)个方程,求解该整合矩阵方程即可求出每个单元节点的状态向量,以此为边值条件,再次利用精细积分法可求出叠层板上任意点的状态向量。
2.2 外载荷的处理
若外载荷为作用于点(x=x0,y=y0)的集中力F,该载荷可用奇异函数表示,将其沿y方向进行傅里叶展开后可得
(13)
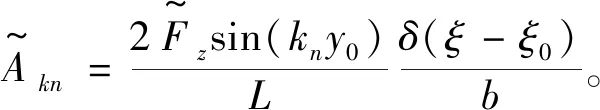
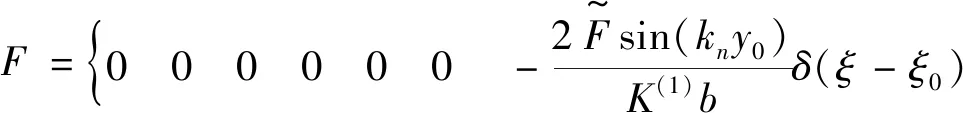
0 0 0 0 0 0 0 0 0}T,将其代入式(11)并积分得
(14)
式中,Z+,Z-为补充单元两端的状态向量。
将式(13)和式(12)联立即可求出各点的状态向量。
若外载荷为均布载荷q,将其沿y方向傅里叶级数展开可得
将式(15)代入式(11),可求解出结构在外载荷下域内各点的状态向量。
3 数值算例

表1 基层板和阻尼层的材料参数Tab.1 Material parameters of the base plate and damping layer

表2 多孔介质的材料参数Tab.2 Material parameters of the porous media

表3 本文模型与有限元模型固有频率的对比Tab.3 Comparison of nature frequencies between the present model and FEM model

图3 本文模型与有限元模型频响曲线的对比Fig.3 Comparison of frequency response curves between the present model and the FEM model
算例2叠层板的结构和参数同算例1,在基板上施加幅值为1 Pa的均布谐激励,单层弹性薄板和叠层板频率响应曲线对比如图4所示。
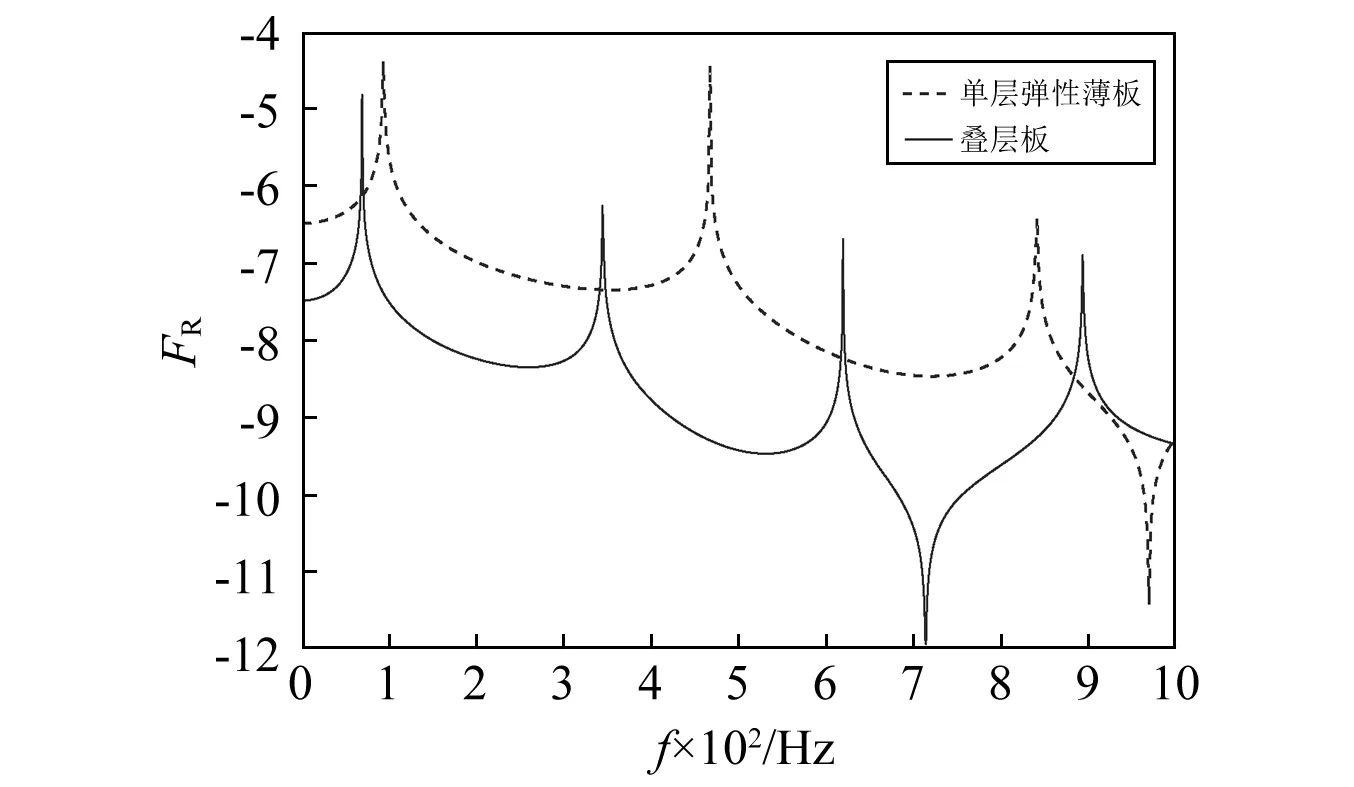
图4 叠层板和单层板频响曲线的对比Fig.4 Comparison of frequency response curves between laminated and single-layer plate
从图4可以明显看出,敷设吸声层和阻尼层后各阶共振频率都降低,共振频率处的位移峰值也明显下降,说明在弹性薄板上敷设多孔介质吸声层和阻尼层可以有效抑制结构的振动。
算例3参数、边界条件和载荷与算例2相同,改变孔隙率、阻尼层厚度、多孔介质层厚度,计算出的频率响应函数如图5~图7所示。由图5可知,在不同的频率范围,孔隙度对阻尼特性的影响不同,并不是孔隙度越大越好。其原因在于,当孔隙率增大时,多孔材料所消耗的振动能量增加,叠层板总体的结构等效质量减小,导致振动时的响应幅值下降。但是,孔隙率增大的同时,多孔介质薄板作为约束材料的刚度下降,导致阻尼层的剪切变形减小,从而对应共振频率处的位移响应幅值就随之下降。因此,需要针对不同的频率范围和参数讨论孔隙率对材料的阻尼特性和振动特性的影响。由图6可知,阻尼层厚度的增加可使结构的固有频率降低,在低频范围内阻尼层的厚度变化对固有频率影响不明显,随着频率增大,阻尼层厚度的影响逐渐增强。总体来说,随着阻尼层的厚度增加,振动时的位移幅值也随之下降。但是,在某些情况下,增加阻尼层厚度,结构的阻尼特性反而下降。文献[18-19]指出,随着黏弹性阻尼材料厚度的增加,叠层板的刚度减小,但惯性会随之增加,导致阻尼层对结构阻尼特性的影响规律较为复杂。由图7可知,多孔介质层厚度的增加的影响规律与图6类似。

图5 不同孔隙率时叠层板频响曲线的对比Fig.5 Comparison of frequency response curves of laminated plate with different porosity

图6 不同阻尼层厚度时叠层板频响曲线的对比Fig.6 Comparison of frequency response curves of laminated plate with different h2
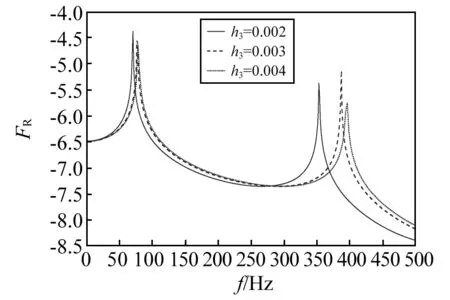
图7 不同多孔介质层厚度时叠层板频响曲线的对比Fig.7 Comparison of frequency response curves of laminated plate with different h3
4 结 论
本文利用薄板理论和Biot 理论,考虑黏弹层的法向平衡方程,以及切向作用力和偏心矩产生的等效力,推导含吸声层和阻尼层叠层板的一阶常微分整合控制方程。结合该模型和高精度的精细积分法,提出了一种分析叠层板结构动力学特性的半解析半数值方法,编制相应 Matlab 程序分析了此类叠层板的谐激励响应,并采用有限元法验证模型的正确性。相对于有限元法,本文方法不需要进行网格划分,可在中高频内保持较高的精度和稳定性,可为后续此类复杂结构的声学和动力学研究提供一种新的思路,具有一定的理论参考价值。

