不同温度环境中沥青混凝土动态抗压性能试验研究
宁致远,刘云贺,王 琦,王为标
(西安理工大学 西北旱区生态水利国家重点实验室,西安 710048)
近年来,随着抽水蓄能电站施工技术上的突破,具有优异防渗性能的沥青混凝土得到了更为广泛的应用,如河北张河湾上库、呼和浩特抽水蓄能电站上库等,均采用了沥青混凝土防渗[1]。这些重点工程多处于温度变化较大的高寒区和无法避让的强震区。因此,结合土石坝防渗面板所处的温度环境,开展沥青混凝土材料动态力学性能研究对其在高寒、高烈度区的应用和发展具有重要意义[2]。
温度是影响沥青混凝土静动力学特性的重要因素。陈宇等[3]认为温度对沥青混凝土的应力-应变特性有显著影响。Wang等[4-5]通过试验表明:当温度分别为3.5 ℃,9 ℃和20 ℃时,沥青混凝土动弹模分别为2 500 MPa,1 900 MPa和900 MPa。Zhang等[6]表明沥青混凝土在20 ℃时的拉伸和弯曲破坏应变是0 ℃时的2~4倍。这些研究成果均是结合某一具体工程在常温或某一特定温度环境中进行的。然而,位于高海拔、高寒区的沥青混凝土防渗面板,温度的变化对其力学性能的影响尤为显著。故沥青混凝土在更广温度区间的力学特性,尤其是动力特性还有待进一步研究。
目前,国内外学者对沥青混凝土的动力特性开展了相关试验研究。余梁蜀等[7]认为沥青含量是影响沥青混凝土动力特性的主要因素。Nakamura[8]通过试验表明应变速率对沥青混凝土的动拉应变破坏有显著影响。Wang等[9]通过剪切试验得到了沥青混凝土剪切模量、剪切强度和黏聚力随应变速率增加而增加的结论。这些研究成果对沥青混凝土材料动力特性的研究起到了很好的推动作用。然而,针对防渗面板所处的温度环境开展沥青混凝土动力特性的研究却只有较少的报道,也未建立动态强度关于温度的计算模型。
鉴于此,本文在-20~30 ℃和10-5~10-2s-1条件下对沥青混凝试件进行了单轴动态抗压试验,分别研究了温度和应变速率对沥青混凝土的抗压强度、弹性模量和峰值应变等力学参数的影响规律。在此基础之上,基于时温等效原理,考虑温度和应变速率的共同作用,建立了沥青混凝土抗压强度和弹性模量的计算模型。
1 试验方案
1.1 配合比及试样制备
根据DL/T 5411—2009《土石坝沥青混凝土面板和心墙设计规范》[10]规范要求,本文中的沥青混凝土设计级配如式(1)所示
(1)
式中:di为筛孔直径;Pi为筛孔直径为di时骨料的通过率,%;P0.074为筛孔直径为0.074时骨料的通过率,%;Dmax为骨料最大粒径,mm;n为级配指数,本文n=0.4。沥青混凝土配合比如表1所示。
本文采用克拉玛依70号沥青,沥青含量为7.0%。沥青混凝土试件采用现场碾压成型,对试件加工得到了高度和直径均为100 mm的圆柱体试件,尺寸偏差满足DL/T 5362—2018《水工沥青混凝土试验规程》[11]规范要求。对沥青混凝土试件进行检测:孔隙率为1.5%~2.1%,密度均大于2.4 g/cm3,矿料技术指标均满足规范和设计要求。

表1 沥青混凝土配合比Tab.1 Asphalt concrete mixture ratio
1.2 试验方案及加载过程
结合土石坝沥青混凝土防渗面板所处的温度环境,以所在地年平均气温变化范围为参考,本文试验温度分别为-20 ℃,-10 ℃,0 ℃,10 ℃,20 ℃和30 ℃。鉴于混凝土类结构在静荷载作用下响应的应变速率范围约为10-6~10-5s-1,在地震作用下响应的应变速率范围约为10-4~10-2s-1[12-14],故本文选取的应变速率分别为10-5s-1,10-4s-1,10-3s-1和10-2s-1。试验过程中通过控制位移速度实现不同应变速率的加载。
本试验在西安理工大学西北旱区生态水利重点实验室进行,试验设备分别为Material Testing System(MTS)静动态试验机和高低温环境箱,试验装置如图1所示。试验加载过程为:①几何对中,将试件放置在MTS静动态试验机上,试件两端涂抹黄油,利用红外线对试件进行几何对中;②物理对中,对试件进行一定预加载,根据位移计读数调整试件对中;③试件恒温,固定高低温环境箱,设置温控参数,将试件恒温24 h;④试件加载,按照预先设定的应变速率加载直至试件破坏。
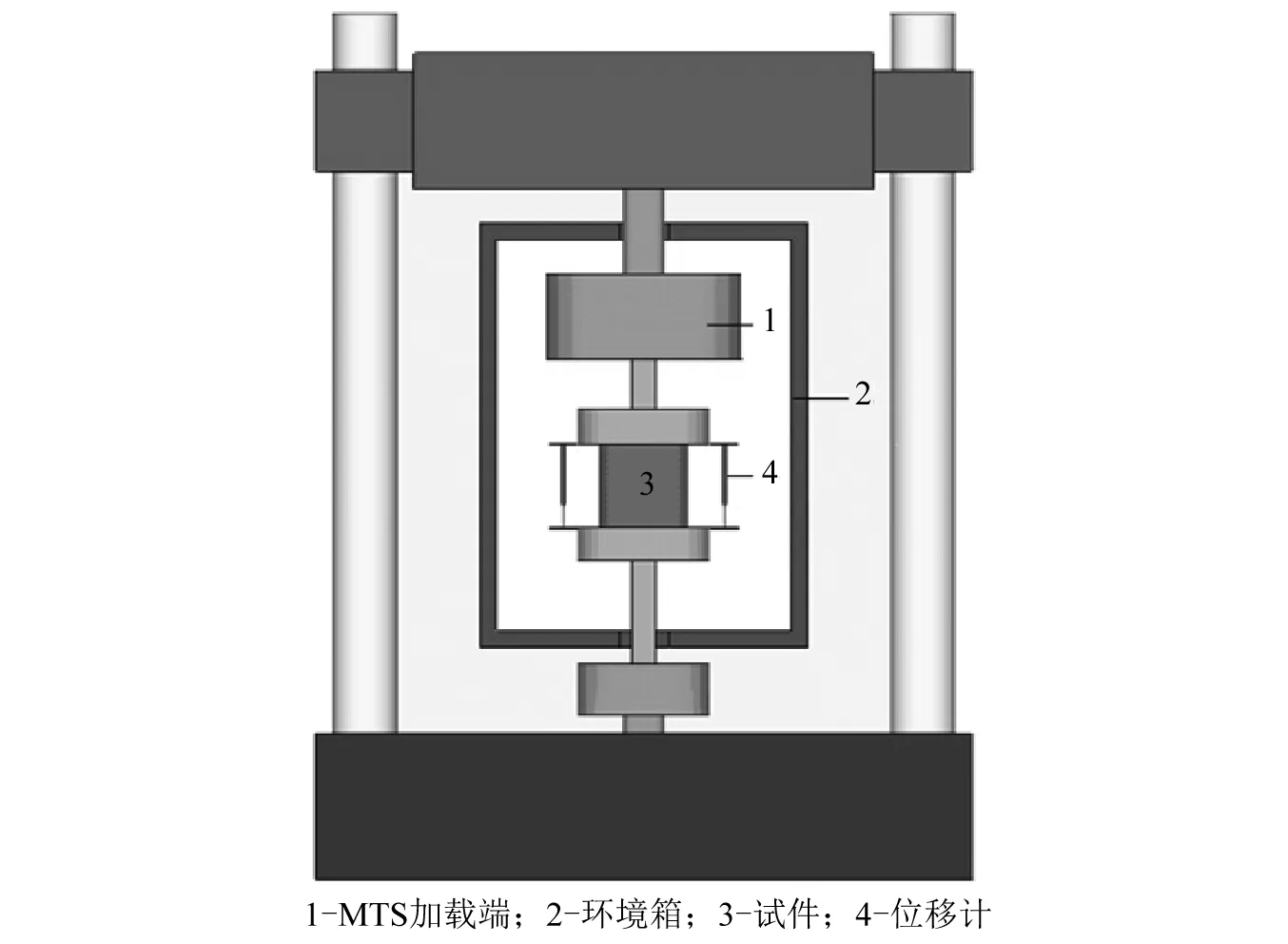
图1 试验装置Fig.1 Test set-up
2 力学参数分析
2.1 抗压强度
不同温度和应变速率条件下沥青混凝土试件的抗压强度,如表2、图2和图3所示。

表2 不同温度和应变速率下沥青混凝土抗压强度Tab.2 Compressive strength of asphalt concrete at different temperatures and strain rates
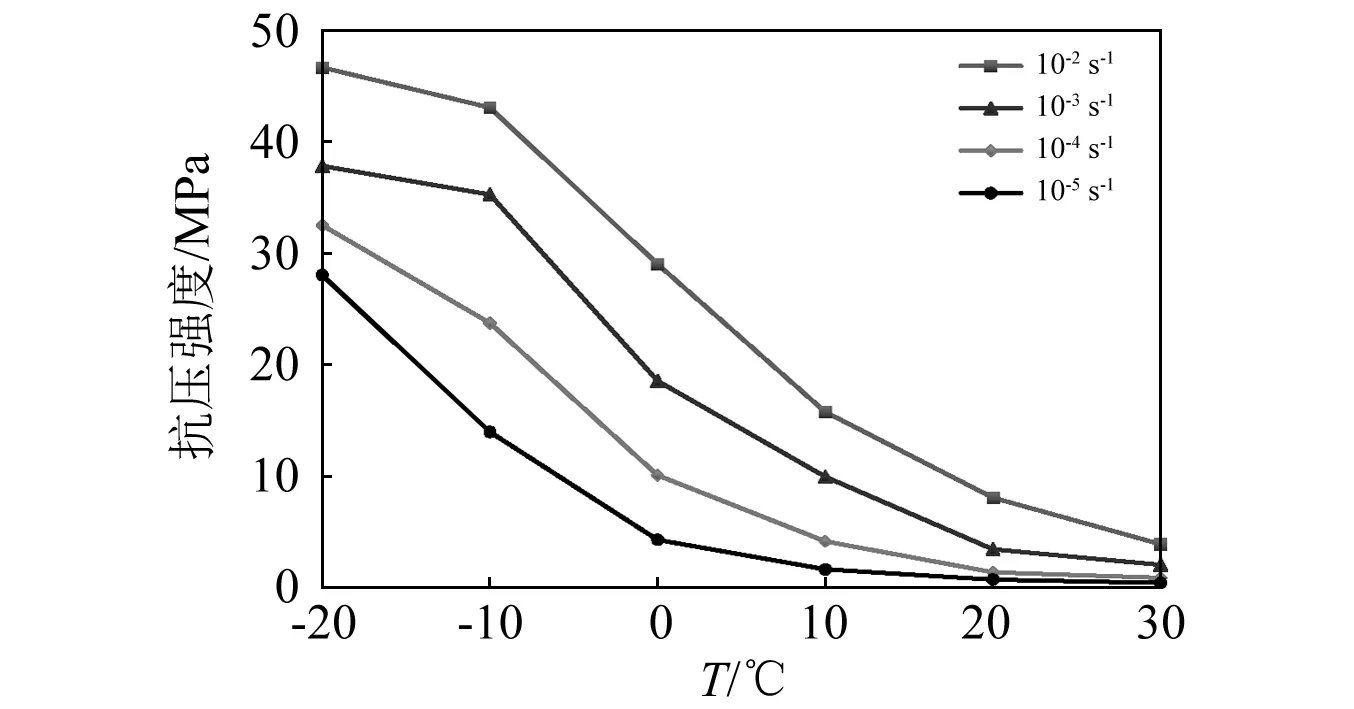
图2 沥青混凝土抗压强度和温度的关系Fig.2 Compressive strength of asphalt concrete vs temperature

图3 沥青混凝土抗压强度和应变率对数的关系Fig.3 Compressive strength of asphalt concrete vs logarithm of strain rate
由表2和图2可知,抗压强度随温度的降低而增大,当试验温度由30 ℃降低到-20 ℃,应变速率为10-5s-1时,抗压强度由0.49 MPa增大至28.05 MPa;当应变速率为10-2s-1时,抗压强度由3.94 MPa增大至46.64 MPa,呈现出明显的温度敏感性。此外,在同一应变速率条件下,随着试验温度的降低,观察到骨料破碎的比例逐渐增大。这是因为沥青混凝土是由骨料、填料以及沥青组合形成的多相复合材料[15]。作为沥青混凝土颗粒增强体的骨料和填料的强度受试验温度(-20~30 ℃)影响极小,而作为胶结材料的沥青受温度影响明显。随着试验温度的降低,沥青材料的分子间距减小,沥青的强度增大[16];同时沥青基质与骨料间的胶结约束作用进一步增强,这一增强的胶结约束作用相当于对较高温度条件下的试件进行了有“侧限”的压缩,故沥青混凝土材料的抗压强度增大。
由表2和图3可知,抗压强度随应变速率的增大而增大,当应变速率由10-5s-1增加到10-2s-1,试验温度为-20 ℃时,抗压强度由28.05 MPa增加到46.64 MPa,增幅为66.3%;当温度为0 ℃时,抗压强度由4.35 MPa增加到29.03 MPa,增幅为567.4%;当试验温度为30 ℃时,抗压强度由0.48 MPa增加到3.94 MPa,增幅为720.8%。温度越高,抗压强度的应变率效应越明显。这主要是因为沥青的力学性能在不同的温度区间有显著差别。当试验温度为0 ℃以及小于0 ℃时,随着应变速率的增加,沥青混凝土的破坏模式由少数主要裂纹扩展为众多裂纹同时存在,这和普通混凝土动力加载时的破坏模式类似。其原因可能是作为胶结材料的沥青基质主要呈弹脆性,导致沥青混凝土抗压强度的应变率效应与岩石、混凝土材料类似。当试验温度大于0 ℃时,沥青主要呈黏弹性,在动应变速率作用下,骨料之间的沥青胶浆受到快速挤压,导致沥青胶浆的黏滞应力迅速增大;并且温度越高,沥青的黏度越高,故由黏性机制引起的应变率效应越显著[17]。
2.2 弹性模量
弹性模量为沥青混凝土应力-应变全曲线上50%峰值应力的点与原点连线的斜率,试验得到了不同温度和应变速率条件下沥青混凝土的弹性模量及变化趋势,如表3、图4和图5所示。

表3 不同温度和应变速率下沥青混凝土弹性模量Tab.3 Elastic modulus of asphalt concrete under different temperatures and strain rates

图4 沥青混凝土弹性模量和温度的关系Fig.4 Elastic modulus of asphalt concrete vs temperature
由表3和图4可知,弹性模量随温度的降低而增大,呈现明显温度敏感性。可解释为随着试验温度降低,沥青材料的分子间距减小,沥青的强度和沥青胶浆与骨料之间的胶结黏聚作用增大,故抵抗单位变形量所需要的外力增大,即沥青混凝土材料的弹性模量也相应增大。值得注意的是,弹性模量随温度的降低并不是无限增大的。试验进一步表明,当温度由-10 ℃降低到-20 ℃时,弹性模量增加幅度逐渐减小。这是因为温度降低到一定值时,沥青与骨料间的胶结约束作用逐渐增至最大,故弹性模量达到最大稳定值。同时,当温度增加到一定值时,沥青与骨料间的胶结约束作用逐渐降低至最小,故弹性模量逐渐达到最小稳定值。

图5 沥青混凝土弹性模量和应变率对数的关系Fig.5 Elastic modulus of asphalt concrete vs logarithm of strain rate
由表3和图5可知,弹性模量随应变速率的增大而增大,当应变速率由10-5s-1增加到10-2s-1,试验温度为-20℃时,弹性模量由1 489.85 MPa增加到4 303.69 MPa,增幅为188.9%;当试验温度为0 ℃时,弹性模量由303.2 MPa增加到2 272.1 MPa,增幅为649.4%;当试验温度为30 ℃时,弹性模量由19.3 MPa增加到204.05 MPa,增幅为957.3%。表明温度越高,弹性模量的应变率效应越显著。总体而言,弹性模量随温度和应变速率的变化规律与抗压强度的变化规律类似。此外,骨料与沥青基质之间的摩擦和嵌挤作用随温度的降低而增大,低温和应变率效应的共同作用进一步促使试件的刚度增大[18]。
2.3 峰值应变
沥青混凝土的峰值应变为其峰值应力所对应的应变,不同温度和应变速率条件下的峰值应变如表4、图6和图7所示。由表4和图6可知,峰值应变随温度的升高而增大,当试验温度由-20 ℃升高到30 ℃,应变速率为10-5s-1时,峰值应变由2.48%升高到5.79%,增幅为133.5%;当应变速率为10-2s-1时,峰值应变由1.18%升高到3.10%,增幅为162.7%。此外,随着试验温度的升高,观察到沥青基质被挤出的现象明显,试件中部产生了较大的膨胀变形。这是因为随着温度的升高,沥青分子间距增大,沥青基质的变形能力增大;此外,在10~30 ℃条件下,裂纹在沥青基质和骨料之间的界面层扩展,作为连续相的沥青基质继续承担外荷载,导致骨料在沥青基质中发生滑动、位错等,进一步提高了试件的峰值应变。
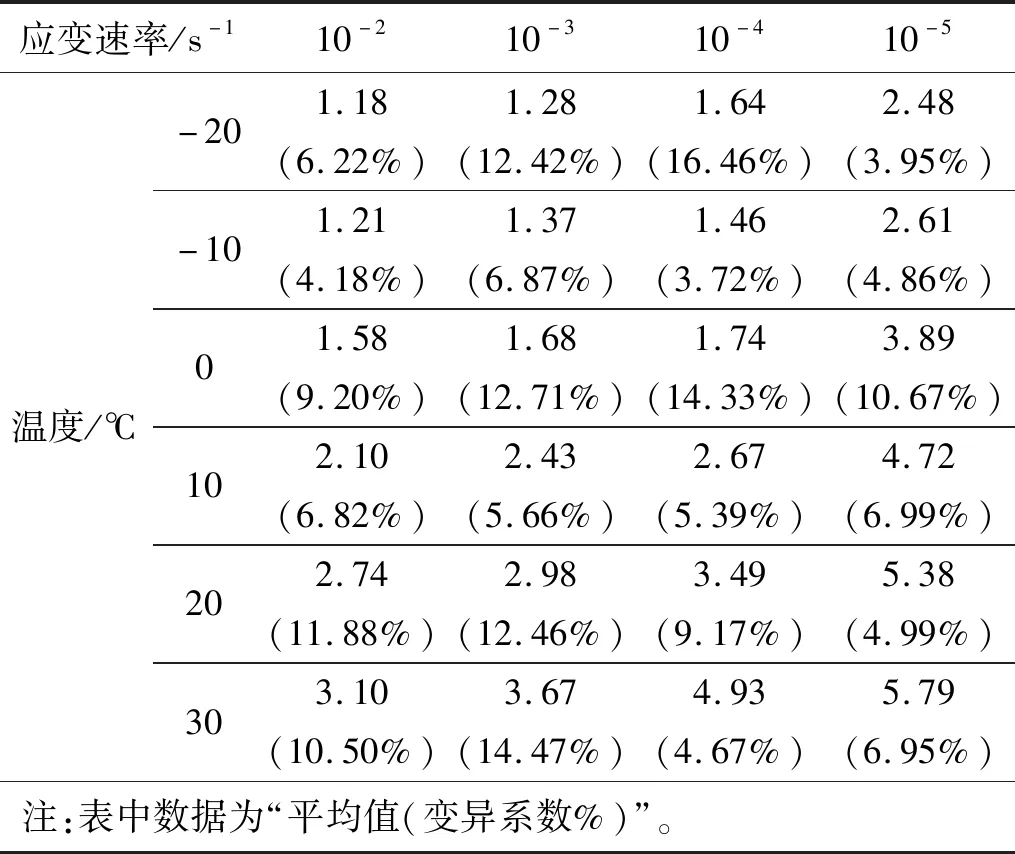
表4 不同温度和应变速率下沥青混凝土峰值应变Tab.4 Peak strain of asphalt concrete under different temperatures and strain rates
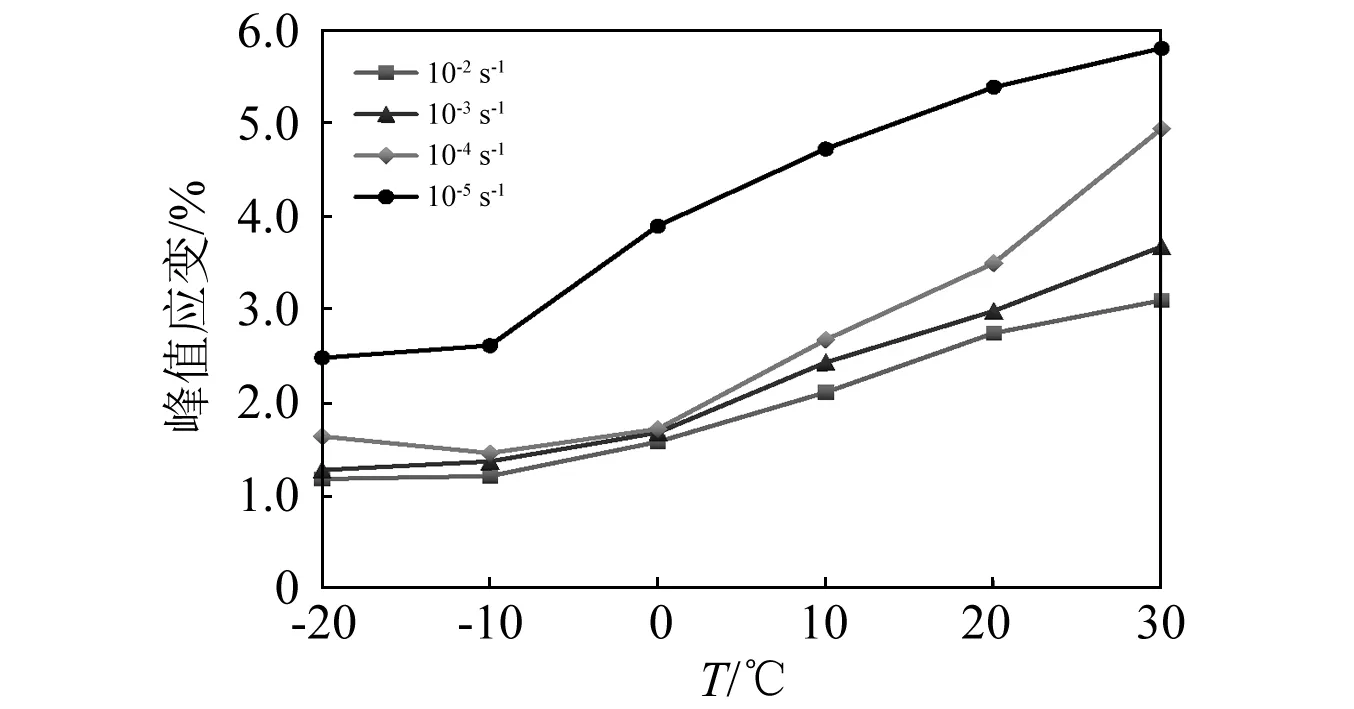
图6 沥青混凝土峰值应变和温度的关系Fig.6 Peak strain of asphalt concrete vs temperature
由表4和图7可知,峰值应变随应变速率的增大而减小,当应变速率由10-5s-1增加到10-2s-1,试验温度为-20 ℃时,峰值应变由2.48%降低到1.18%,降幅为52.4%;当试验温度为0 ℃时,峰值应变由3.89%降低到1.58%,降幅为59.4%;当试验温度为30 ℃时,峰值应变由5.79%降低到3.10%,降幅为46.5%。这是因为在准静态荷载作用下,沥青基质有充足的时间变形;随着加载速率的增大,裂纹萌发和扩展的时间越来越短,导致沥青基质还未充分变形,试件随即发生破坏。进一步对比图6和图7可知,当试验温度为-20 ℃,-10 ℃和0 ℃时,沥青混凝土在10-4~10-2s-1条件下的峰值应变较为接近。结合前述分析,其原因可能是当温度为0 ℃以及小于0 ℃时,沥青混凝土主要呈弹脆性,故动应变速率作用下的峰值应变在低温条件下变化不明显,呈现出普通混凝土的特点。由于混凝土类材料各组分具有随机分布的性质,以及其力学特性受到材料配合比、成型方式等多种因素的影响,这一现象还有待进一步验证。

图7 沥青混凝土峰值应变和应变率对数的关系Fig.7 Peak strain of asphalt concrete vs logarithm of strain rate
3 抗压强度和弹性模量计算模型
3.1 温度影响因子
为进一步研究沥青混凝土的抗压强度和弹性模量随温度变化的规律,引入了温度影响因子(Temperature Influence Factor,TIF)[19]。抗压强度(或弹性模量)温度影响因子定义为应变速率恒定时,任一温度条件下抗压强度(或弹性模量)的值与温度为0 ℃时的比值,即Tσ。以抗压强度温度影响因子为例说明,如式(2)所示
(2)
式中:σT为任一温度条件下的抗压强度;σ0为0 ℃时的抗压强度。由表2计算得到了10-5~10-2s-1条件下抗压强度温度影响因子Tσ,如图8所示。由图8可知,当试验温度大于0 ℃时,准静态和动荷载作用下抗压强度温度影响因子随温度变化规律相同;当温度小于0 ℃,应变速率由10-5s-1增大到10-2s-1时,观察到抗压强度温度影响因子随试验温度的降低逐渐趋于某一最大值,其变化规律类似于反“S”型。故可采用Logistic函数形式[20]描述沥青混凝土抗压强度温度影响因子随温度变化的规律,如式(3)所示
(3)
式中:ωσ,ξσ为材料参数;T*为等效温度[21],如式(4)所示
(4)
式中:Tr为材料参考温度;Tm为材料熔点温度。本文中沥青混凝土的参考温度取0 ℃,熔点温度取150 ℃[22]。由式(2)~式(4)计算得到了各应变速率条件下抗压强度温度影响因子随温度变化的规律,如图8所示,ωσ,ξσ及相关系数R2如表5所示。
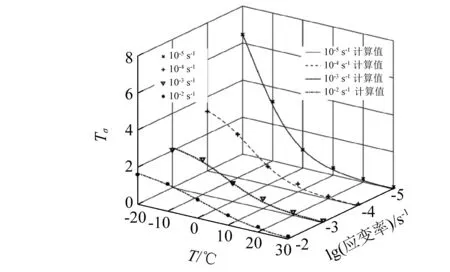
图8 抗压强度温度影响因子与温度的关系Fig.8 TIFs of compressive strength vs temperature
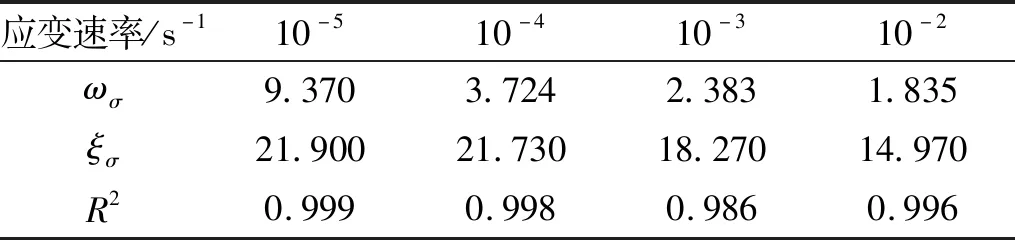
表5 不同应变速率条件下材料参数ωσ,ξσ值Tab.5 Parameters ωσ and ξσ under different strain rates
由表3计算得到了10-5~10-2s-1应变速率条件下弹性模量温度影响因子TE,如图9所示。由图9可知,弹性模量温度影响因子的变化规律与抗压强度温度影响因子变化规律类似,故采用同样的方法描述不同应变速率条件下弹性模量温度影响因子随温度变化的趋势。ωE,ξE及相关系数R2,如表6所示。
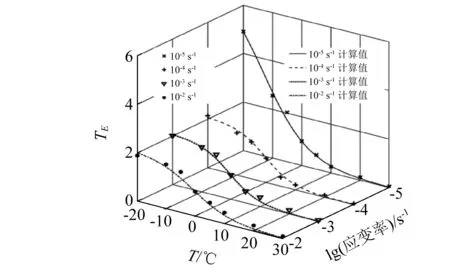
图9 弹性模量温度影响因子与温度的关系Fig.9 TIFs of elastic modulus vs temperature

表6 不同应变速率条件下材料参数ωE,ξE值Tab.6 Parameters ωE and ξE under different strain rates
综合上述分析,由式(2)~式(4)计算得到的抗压强度和弹性模量温度影响因子与试验结果吻合较好(见图8和图9),较好地反映了沥青混凝土材料在各应变速率作用下的温度敏感特性。
3.2 动态增强因子
动态增强因子(Dynamic Increase Factor,DIF)用于描述岩石、混凝土类材料抗压强度和弹性模量在动应变速率条件下的增长特性。沥青混凝土抗压强度(或弹性模量)动态增强因子定义为温度恒定时,动应变速率条件下抗压强度(或弹性模量)的值与准静态时的比值Dσ。以抗压强度动态增强因子为例说明,如式(5)所示
(5)
式中:σd为应变速率为10-4s-1,10-3s-1和10-2s-1作用下的抗压强度;σs为应变速率为10-5s-1作用下的抗压强度。由表2计算得到了-20~30 ℃条件下沥青混凝土抗压强度动态强度增强因子Dσ,如图10所示。由图10可知,当温度为-20~0 ℃时,抗压强度动态强度增强因子随应变速率呈线性增长关系,并且温度越低,抗压强度动态增强因子增长速度越缓慢。当温度为0~30 ℃时,抗压强度动态强度增强因子随应变速率呈非线性增长关系。

图10 抗压强度动态增强因子与应变率对数的关系Fig.10 DIFs of compressive strength vs logarithm of strain rate
本文中,采用式(6)描述-20~0 ℃条件下抗压强度动态增强因子随应变速率线性增长的变化规律,在式(6)的基础上进行变化,采用式(7)描述0~30 ℃条件下抗压强度动态增强因子随应变速率非线性增长的变化规律。
(6)
(7)
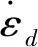

表7 不同温度条件下参数aσ值Tab.7 Parameter aσ under different temperatures
由表3计算得到了-20~30 ℃条件下弹性模量动态增强因子DE,如图11所示。由图11可知,弹性模量动态增强因子的变化规律与抗压强度动态增强因子变化规律类似,故采用同样的方法描述-20~0 ℃和0~30 ℃条件下弹性模量动态增强因子随应变速率的变化规律。参数aE及相关系数R2,如表8所示。

图11 弹性模量动态增强因子与应变率对数的关系Fig.11 DIFs of elastic modulus vs logarithm of strain rate

表8 不同温度条件下参数aE值Tab.8 Parameter aE under different temperatures
综合上述分析,沥青混凝土的抗压强度和弹性模量具有显著的应变率效应,在-20~0 ℃温度区间,抗压强度和弹性模量的动态增强因子随应变速率呈线性增长;在0~30 ℃温度区间,抗压强度和弹性模量的动态增强因子随应变速率呈非线性增长。式(6)和式(7)较好地反映了不同温度条件下抗压强度和弹性模量动态增强因子随应变速率变化的规律,与试验结果吻合较好(见图10和图11)。
3.3 抗压强度和弹性模量计算模型
沥青混凝土是典型的黏弹性材料,具有时温等效性[23],即沥青混凝土材料在高温条件下的力学性能可通过延长加载时间获得。本节在3.1节和3.2节研究的基础上,考虑温度和应变速率共同作用,建立抗压强度和弹性模量的计算模型。本文中“时间”为应变速率。根据时温等效原理,若要确定任意应变速率下抗压强度(或弹性模量)随温度变化的规律,可将参考应变速率下抗压强度(或弹性模量)与温度变化的主曲线平移一定的水平距离获得,如式(8)所示
(8)
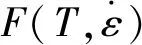
(9)
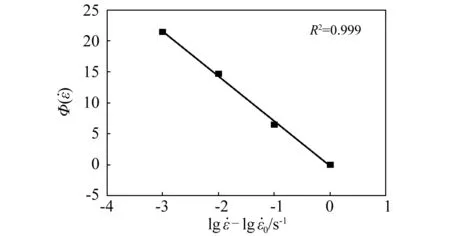
图12 时温变换因子与应变率对数的关系Fig.12 The time-temperature transformation factor vs logarithm of strain rate
由式(6)和式(9),得到了抗压强度随温度和应变速率变化的主曲面,如式(10)、图13所示。
(10)
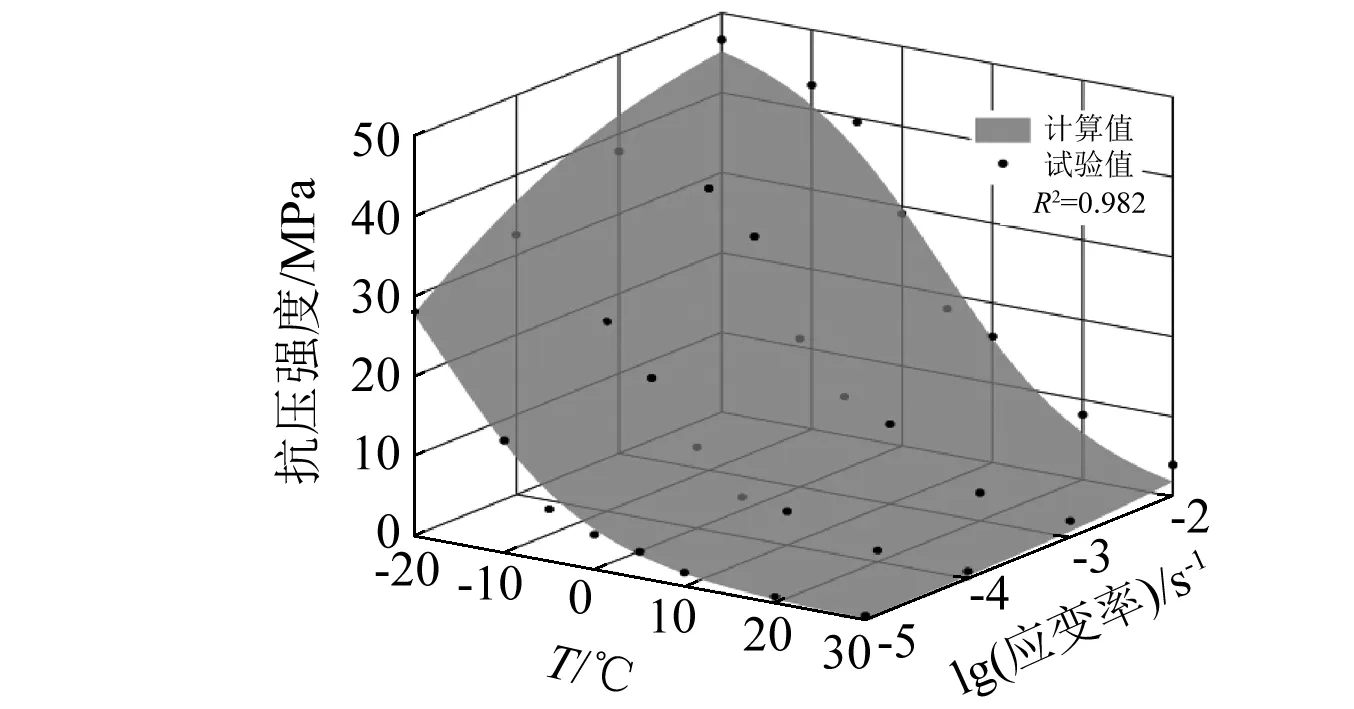
图13 沥青混凝土抗压强度计算值与试验值对比Fig.13 The calculated value of compressive strength of asphalt concrete vs test values
同理,沥青混凝土弹性模量随温度和应变速率变化的主曲面如式(11)、图14所示。
(11)
综合上述分析,由图13和图14可知,基于时温等效原理,得到了抗压强度和弹性模量的计算模型,与试验结果吻合较好。该计算模型较好地反映了沥青混凝土材料在温度和应变速率共同作用下的动态抗压力学特征。当试验条件受限时,可预测沥青混凝土在更高应变速率或更低温度条件下的抗压强度或弹性模量。
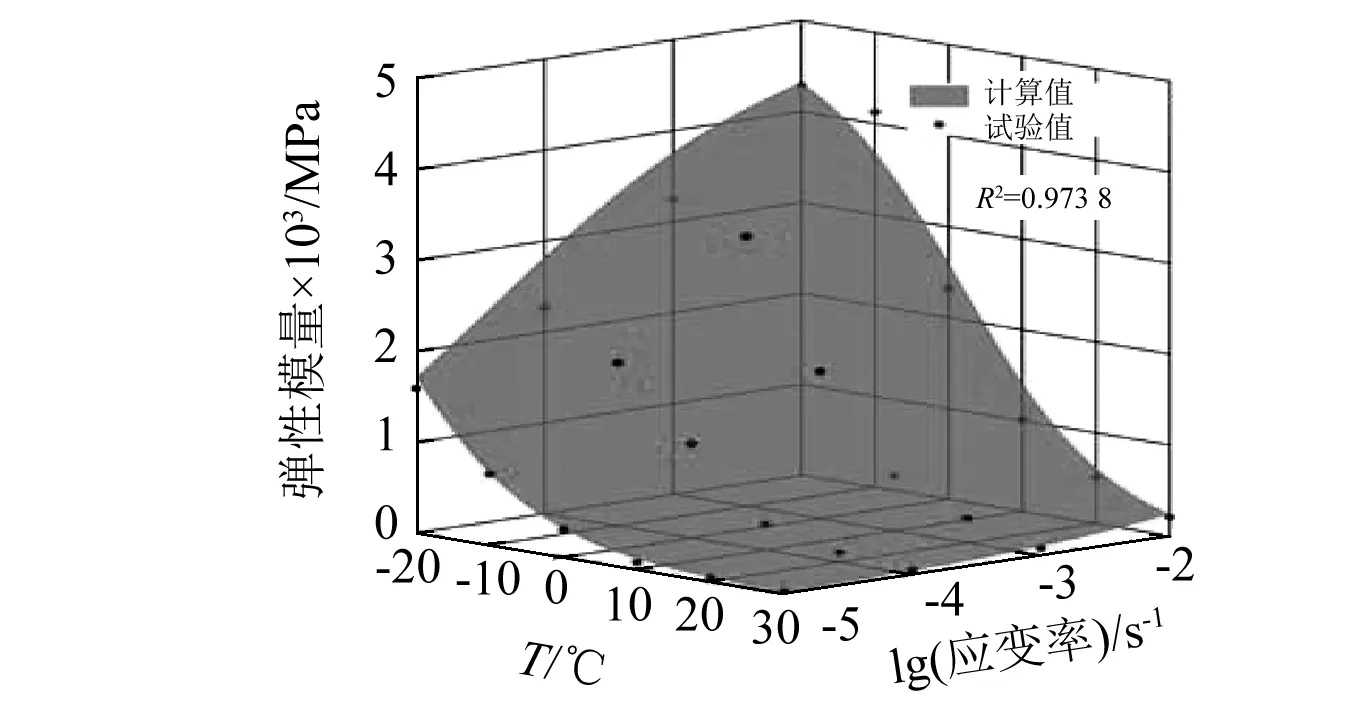
图14 沥青混凝土弹性模量计算值与试验值对比Fig.14 The calculated value of elastic modulus of asphalt concrete vs test values
4 结 论
本文在温度为-20~30 ℃和应变速率为10-5~10-2s-1条件下对沥青混凝土试件进行了单轴动态抗压试验研究,研究了温度和应变速率对沥青混凝土动态抗压性能的影响,基于时温等效原理,建立了沥青混凝土抗压强度和弹性模量的计算模型,主要得到了以下结论:
抗压强度和弹性模量随温度的降低而增加,当温度大于20 ℃或小于-10 ℃,应变速率由10-5s-1增加到10-2s-1时,温度对抗压强度和弹性模量的影响逐渐减小。本文提出的温度影响因子经验公式较好地反映了各应变速率条件下抗压强度和弹性模量随温度变化的规律,与试验数据吻合较好。
抗压强度和弹性模量随应变速率的增加而增加,具有显著的应变率效应,在-20~0 ℃时,抗压强度和弹性模量动态增强因子随应变速率呈线性增长;在0~30 ℃时,抗压强度和弹性模量动态增强因子随应变速率呈非线性增长。
峰值应变随应变速率的增加而减小,随温度的升高而增大。当温度为0 ℃或低于0 ℃时,动应变速率作用下沥青混凝土的峰值应变较为接近;当温度大于0 ℃时,应变速率越快,峰值应变的变化越明显。
在深入研究沥青混凝土温度影响因子和动态增强因子关系的基础上,基于时温等效原理,建立了沥青混凝土抗压强度和弹性模量的计算模型。该模型反映了沥青混凝土材料在不同温度和应变速率共同作用下的温度敏感性和应变率效应,与试验结果吻合较好。

