考虑风电出力不确定性的配电网概率潮流计算

白 洁，王守相，赵倩宇，廖文龙，赵海洲，张 雷

（1.天津大学智能电网教育部重点实验室，天津 300072；2.国网河北省电力有限公司衡水供电分公司，衡水 053000）

风电接入配电网导致电能质量下降，电压问题突出且风电出力的随机性和间歇性增加了配电网运行的不确定性。概率潮流计算可以全面反映不确定性对系统运行状态的影响，是电力系统规划和安全可靠分析的重要工具[1-2]。

蒙特卡洛模拟法[3]计算精度高且能得到输出随机变量的概率分布，但需要建立精确的输入变量概率模型。建立风速概率模型的方法包括参数法和非参数法。参数法通过假定研究对象服从的概率分布模型并估计其中的参数从而得到具体的分布函数。目前风速常用的分布函数有威布尔分布[4]、高斯分布[5]等，而假设的概率模型是否合理直接影响潮流计算结果的准确性。非参数法[6-7]从数据本身出发，直接研究数据的分布特征，无需对研究对象进行模型假定。虽然解决了概率模型假设不合理的问题，但核函数的选择、参数的求解仍是难题。

当系统中包含多个输入变量时，需要考虑变量之间的相关性。多风电出力相关性建模常用的方法有空间变换法[8]和Copula函数分析法[9]。其中，空间变换法只能描述一种相关性，而Copula函数分析法对于高维随机变量有很大局限性，且两种方法的计算过程复杂繁琐。综上分析，目前考虑风电出力不确定性的配电网潮流计算难点在于：（1）如何精确描述潮流计算中风功率的概率分布；（2）怎样有效处理区域内风功率输出的复杂相关性。

近年来，随着深度学习的广泛开展和应用，其在电力系统中受到越来越多的重视。文献[10]利用生成对抗网络GAN（generative adversarial network）实现风电和光伏功率输出的场景生成，无需概率建模，完全数据驱动，有效弥补了现有基于概率模型的场景生成方法的不足。文献[11]为避免GAN训练不收敛，提出了一种基于条件变分自动编码器VAE（variational automatic encoder）的风电和光伏场景生成方法。将文献[10-11]生成的随机场景作为概率潮流计算的输入，可以有效解决考虑可再生能源不确定性潮流计算中遇到的两个难点，且目前尚未有研究采用生成模型产生的样本进行概率潮流计算。

为解决考虑风电出力不确定性的概率潮流计算中风速概率模型准确性差、求解参数复杂及多风机出力相关性难以考虑的难题，本文提出一种基于双向生成对抗网络BIGAN（bidirectional generative adversarial network）描述风功率分布的数据生成模型，在此基础上，将生成的风功率样本作为输入随机变量进行潮流计算。最后，在IEEE 33节点系统中验证了本文方法的准确性和有效性。

1 双向生成对抗网络

1.1 BIGAN的基本原理

GAN和VAE是常见的生成模型，在无监督学习中起着重要的作用。其中，VAE的拓扑结构中没有判别器，没有使用对抗网络，所以产生的图片趋向于模糊。为解决这个问题，Goodfellow等[12]提出具有对抗思想的神经网络，即GAN。GAN由生成器和判别器构成，核心思想是设置一个零和博弈，通过生成器和判别器的对抗学习数据的概率分布，其拓扑结构如图1所示。生成器生成逼真的样本G(z)，判别器鉴别输入样本是真实数据x还是生成数据G(z)，生成器和判别器不断提高自身的生成能力和判别能力，最终达到或逼近纳什均衡，即判别器无法区别真实数据和生成数据[12]。

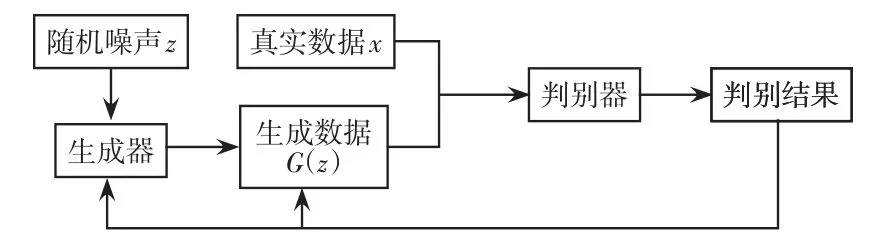
图1 GAN的拓扑结构Fig.1 Topology of GAN

GAN的目标函数V(G,D)为[13]

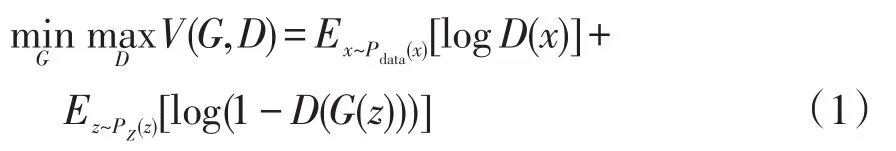
式中：x服从真实数据分布Pdata(x)；z服从先验分布Pz(z)，一般为高斯分布。

在GAN训练过程中，先固定生成器，优化判别器。其判别器是一个二分类模型，训练判别器是最大化交叉熵的过程。再固定判别器，优化生成器。生成器以随机噪声z为输入，构造映射函数G(z,θG)，输出表示生成的样本；对应的判别器映射函数为D(x,θD)，输出表示判别器判断输入数据为真实数据的概率。其中，θG、θD是生成器和判别器的参数。生成器的作用是让生成的数据尽可能地接近真实数据，即D(G(z))越接近1越好，此时V(G,D)会减小。判别器的作用是让D(x)接近1，而D(G(z))接近0，此时V(G,D)会增大。因此，整个GAN的优化是一个极大—极小问题[14]。

BIGAN是对GAN的一种改进，可将真实数据x映射到隐变量空间，实现对真实数据的特征提取。其原理与GAN的原理相似，但在拓扑结构上添加了编码器，具体结构如图2所示。

图2 BIGAN的拓扑结构Fig.2 Topology of BIGAN

BIGAN的优化思路如下：

（1）输入真实数据x，经过编码器得到E(x)；

（2）从先验分布中采样随机噪声z，经过生成器得到G(z)；

（3）经过上述两步，得到(x,E(x))和(z,G(z))，并将这两个数据对输入判别器中，让判别器区分输入数据对是由编码器还是由生成器产生。

生成器、编码器和判别器的博弈可理解为生成器和编码器是否能够欺骗判别器，让判别器无法分辨输入数据对的来源，BIGAN的目标函数为[15]

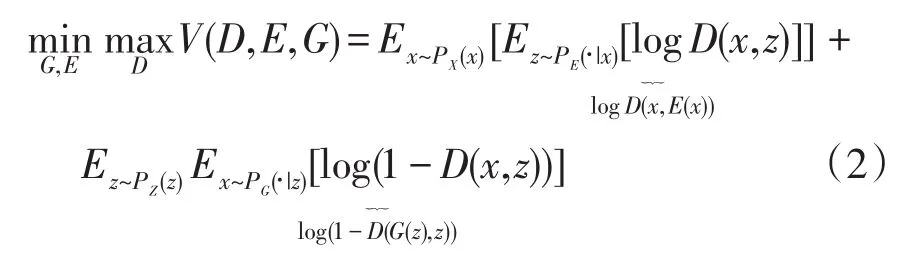
式（2）和GAN的目标函数式（1）相比，区别在于D(x)变成了D(x,E(x))，D(G(z))变成了D(G(z),z)。此目标函数实现x=G(E(x))，z=E(G(z))的证明过程见文献[15]。

1.2 BIGAN的训练过程

本文BIGAN中编码器、生成器、判别器的网络结构采用全连接层构建的多层感知机MLP（multilayer perceptron）。MLP包括输入层、隐藏层和输出层。其中，隐藏层输出值Hj和输出层输出值Ok的表达式[16]为

式中：i、j、k代表输入层、隐藏层和输出层，各层的神经元个数为L、M、N；f是神经网络的传递函数；Pi表示输入数据；Wij为从输入层到隐藏层的权值矩阵，Wjk为从隐藏层到输出层的权值矩阵；θj、ϕk分别是隐藏层和输出层的阈值向量。

BIGAN在训练过程中先固定生成器和编码器，优化判别器，输入数据经过神经网络的前向传播得到输出，计算判别器的损失函数，再由梯度反向传播更新判别器的参数。然后固定判别器，优化生成器和编码器的参数。图3所示为BIGAN的训练过程。

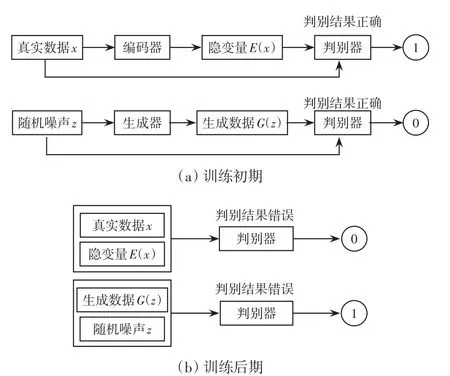
图3 BIGAN的训练过程Fig.3 Training process of BIGAN

在训练前期，判别器对输入的(x,E(x))和(z,G(z))数据对可以正确判断出(x,E(x))来自编码器，(z,G(z))来自生成器。随着训练次数的增加，编码器将真实数据转换成先验分布、生成器将先验分布转换成真实数据的能力不断提高，判别器无法正确做出判断，说明训练成功。

2 基于BIGAN刻画风电出力不确定性的概率潮流计算

2.1 BIGAN刻画风电出力的不确定性

与图像生成不同的是，BIGAN学习的风功率数据受大气和各发电单元空间关系等物理因素的影响。首先输入原始风功率数据，BIGAN自主学习原始数据的统计规律，并基于训练好的模型生成符合原始数据统计特点的样本。具体步骤如下：

步骤1导入多个风电机组的数据，采用最大-最小标准化方法，将输入数据映射到区间[-1，1]中，并利用Reshape函数将一维的风功率数据变成二维的数据矩阵；

步骤2计算整个网络的目标函数，进行迭代训练。在训练过程中，编码器以真实数据x为输入，产生尽可能和高斯分布相似的隐变量E(x)，生成器以服从高斯分布的一维随机噪声z为输入，产生尽可能和真实数据相似的样本G(z)，判别器以(x,E(x))和(z,G(z))两组数据对为输入，区分它们来自编码器还是生成器。整个训练过程处于动态博弈过程；

步骤3如果达到预先设定的迭代次数或者达到纳什平衡，则进行步骤4，否则，返回步骤2继续迭代；

步骤4迭代完成后，BIGAN学习到了多个风电机组的联合概率分布特征，截取生成器作为生成模型，输入随机噪声z，即可得到二维矩阵，利用Re⁃shape将二维数据矩阵变换成一维的风功率曲线，并进行反归一化得到符合原始数据概率分布的全新数据。

2.2 概率潮流计算数学模型

考虑风电出力不确定性的配电网概率潮流计算的基本模型[17]为

式中：Y是节点注入功率；V为节点电压；Z为支路功率；函数f(∙)、g(∙)是确定性潮流方程。因Y受负荷和接入风电机组出力波动的影响而成为随机变量，所以V、Z也变为随机变量。

2.3 概率潮流计算流程

基于BIGAN考虑风电出力不确定性的配电网概率潮流计算包括两大部分：（1）BIGAN产生符合原始数据概率分布的风功率样本；（2）进行概率潮流计算并对结果做统计分析。具体步骤如下：

步骤1由2.1节生成模型建立流程得到符合原始风功率概率分布的多维随机变量样本；

步骤2负荷的随机性用正态分布表示，均值为原始系统参数值，方差是均值的10%；

步骤3将风电机组和负荷的样本作为潮流计算的输入随机变量Y，代入式（5），采用前推回代法计算输出随机变量V和Z，并进行统计分析。

3 算例分析

3.1 BIGAN生成数据的效果验证

为了验证BIGAN刻画风电出力不确定性的有效性，以美国某地区9个风电机组从2012年1月1日到2012年12月31日的实际数据为仿真数据，随机选取90%的数据作为训练集，剩下10%的数据作为测试集。训练样本包括9个风电机组的功率，数据采样间隔是10 min，即一天中每个风电机组包括144个数据。因此，每个样本一天有129 6个数据点，将这129 6个点重塑为36×36的矩阵作为训练集，整体在Keras平台上测试。

根据风功率数据的特点，本文设计的编码器、生成器、判别器网络结构如图4所示。为加快模型收敛速度，全连接层都采用LeakyReLU激活函数，alpha是0.2。生成器的输出层使用Tanh函数，判别器的输出层采用Sigmoid激活函数。为防止过拟合，在判别器的全连接层后添加数值为0.25的Dropout层。各层输入前添加分批标准化层，动量momentum为0.8。训练的批梯度下降大小为32，优化器选用Adam，学习率设定为0.000 2，总迭代次数是5 000。

图4 BIGAN的网络结构参数Fig.4 Network structure parameters of BIGAN

训练好生成网络后，输入100组维度为10且服从高斯分布的随机噪声z，通过生成器可得到100组风功率生成样本。计算生成的100组风功率曲线和测试集中真实的风功率曲线之间的欧式距离，并选出距离最小的一组曲线，如图5（a）所示。计算这组曲线的自相关系数，如图5（b）所示。

由图5可知，尽管测试集不参与训练，生成器却能模拟出和真实数据高度相似的风功率曲线，这说明BIGAN能够产生符合实际情况的数据。另外，从自相关函数可以看出，生成的风功率曲线较好地还原了真实风功率曲线的时间相关性。

图5 生成数据和真实数据的风功率曲线和自相关系数Fig.5 Wind power curve and auto-correlation coefficient of generated and real data

在风功率短期特性验证的基础上，分析其长期特性。对366组真实数据和100组生成数据的概率分布进行统计分析，生成数据和真实数据的概率分布如图6所示。由图6可知，相比于传统方法，BIGAN生成的数据较好拟合了真实风功率的概率分布，说明BIGAN学习到了真实数据之间的分布规律。

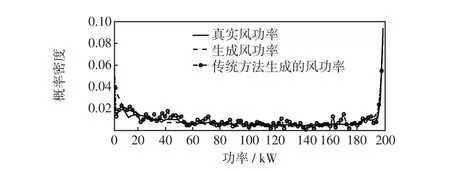
图6 生成数据和真实数据的概率分布Fig.6 Probability distribution of generated and real data

以上风功率的短期特性、自相关系数、概率分布都是对单个风电机组的验证。仿真数据是美国某地区相邻的9个风电机组，这些发电单元的地理位置比较接近，它们的出力具有一定的空间相关性。为此，选用皮尔逊系数对BIGAN生成数据的相关性进行验证，图7展示了9个风电机组真实和生成数据的皮尔逊系数矩阵差的绝对值。

图7 皮尔逊系数矩阵差的绝对值Fig.7 Absolute values of Pearson coefficient matrix difference

由图7可知，皮尔逊系数之差不大于0.086。这说明生成对抗网络在生成多个风电机组功率的同时，还能很好地捕获风电机组之间的相关性。

综合上述分析，BIGAN能同时刻画风功率的时间相关性、概率分布特性，以及多个风电机组的空间相关性，整个过程无需人工干预，完全数据驱动。与传统概率模型相比，产生的风电功率数据更能代表实际运行状况。

3.2 考虑风电出力不确定性的概率潮流计算

3.2.1 系统参数

选用IEEE 33节点配电网作为本文算例[1]进行概率潮流计算。在节点10、13、15接入风电机组，功率因数为0.9。假设各节点的负荷服从正态分布，均值为原始系统参数值，方差是均值的10%。

3.2.2 潮流计算结果分析

从3.1节9个风电机组中选择前3个接入系统进行潮流计算。以BIGAN生成的100×144个样本和服从正态分布的负荷样本为输入随机变量，进行14 400次前推回代确定性潮流计算，然后统计分析输出随机变量的数字特征和概率分布，以上方法记为“本文方法”。时序法以366×144个历史风功率数据为输入进行52 704次潮流计算[18]。将时序法作为参考标准，检验本文方法的计算精度，并采用蒙特卡洛采样-Cholesky分解法排序的传统方法进行对比。

由非参数核密度估计法得到原始数据中3个风电机组出力的概率密度，如图8所示。由图8可见，风功率的概率密度曲线存在差异，难以用统一的概率模型描述分布特性。因此，采用本文提出的BIGAN方法描述风电出力的不确定性。

图8 3个风电机组出力的概率密度Fig.8 Probability density of output from three wind turbines

在进行概率潮流计算后，通过统计计算结果，节点18电压的均值、标准差及越下限概率（以最大允许电压偏移7%为标准）如表1所示。

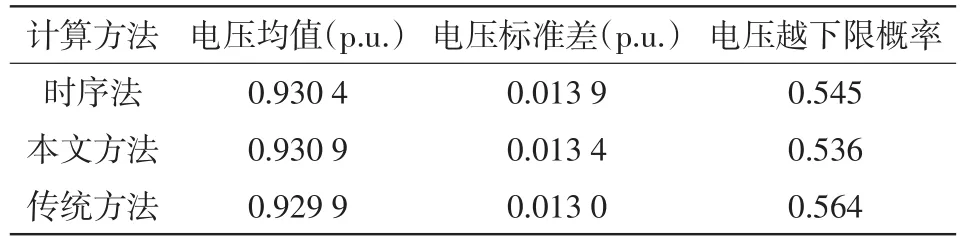
表1 节点18电压的数字特征Tab.1 Digital features of voltage at bus 18

由表1可知，本文方法相比于时序法，电压均值的相对误差小于0.05%，标准差的相对误差小于3.6%，越下限概率的相对误差小于1.65%，且电压标准差和电压越下限概率的误差相比于传统方法减少约50%。由此可见，本文方法的计算精度较高。

为进一步观察节点18电压的概率分布，图9给出了电压幅值的概率密度。由图9可知，相比于传统方法，本文方法得到的节点18电压上下限及波动变化更贴近时序方法的计算结果。

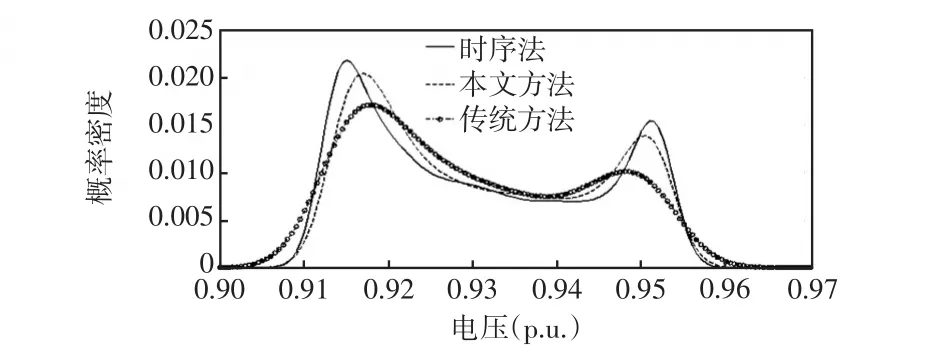
图9 节点18电压的概率密度Fig.9 Probability density of voltage at bus 18

概率潮流计算的输出除了节点电压还有各支路的有功功率、无功功率，为进一步验证本文方法的计算精度，对有功损耗和无功损耗的数字特征、概率密度进行对比分析。表2为网络损耗的数字特征。

由表2可知，本文方法计算得到的有功损耗均值、标准差及无功损耗均值、标准差和时序法非常接近。在网络损耗的数字特征方面，传统方法与本文方法相差无几，都非常接近时序法的计算结果。

表2 网络损耗的数字特征Tab.2 Digital characteristics of network lossp.u.

图10为有功损耗和无功损耗的概率密度。从图中可以得到，相比于传统方法，本文方法计算得到的输出随机变量概率分布与时序法的计算结果更吻合，表现在输出随机变量的上下限及曲线的波动变化趋势。

图10 有功损耗和无功损耗的概率密度Fig.10 Probability density of active and reactive power loss

综上分析，本文概率潮流计算的结果在数字特征、概率分布方面与时序法计算结果一致，计算精度较高，且减少了潮流计算的次数，节省了计算时间。

4 结论

本文提出了一种基于BIGAN描述风电出力不确定性的概率潮流计算方法，可以准确全面地刻画风电出力的不确定性及多个风机出力的相关性，为含多个风电机组的配电网概率潮流计算提供了新方法。通过对BIGAN的验证和在IEEE 33节点系统中的潮流计算结果分析，验证了所提方法的正确性和有效性，并得到以下结论：

（1）提出的BIGAN方法无显式概率建模，完全数据驱动。经验证，产生的样本不仅能精确模拟风功率的时间相关性、概率分布特性，还能计及多个风机的空间相关性；

（2）提出的BIGAN方法易于扩展，不仅可描述多个风机的出力，也可描述于多个光伏的出力，或者风电和光伏的联合出力；

（3）基于BIGAN的潮流计算方法可以全面给出输出随机变量的数字特征和概率密度；

（4）所提方法相比于传统方法计算精度更高，且比时序法潮流计算的次数减少，节省了计算时间，具有实际应用价值。