应用抗扰动观测器的微网改进下垂无功补偿技术

谢 楠 ，杨沛豪 ，何 萍 ，袁训锋 ，陈 垚

（1.商洛学院电子信息与电气工程学院，商洛 726000；2.商洛市新能源研发平台，商洛 726000；3.西安热工研究院有限公司，西安 710054；4.国网吴忠供电公司，吴忠 751100）

随着电网容量不断增加，为了实现可再生能源规模化应用，需要大力发展微网[1-2]。微网通过公共接入点PCC（public connection point）与公共电网并列运行，电压受公共电网牵制[3]。当微网处于孤网运行时，由于内部电源点的出力随机性及微网系统本身低惯量特性，母线电压易受负荷功率波动等因素影响。如何对分布式电源DG（distributed generation）的逆变装置合理控制，成为最近的研究热点[4-5]。

在微网逆变装置控制系统中，大多采用PQ下垂控制和恒压恒频（V-f）控制[6]。传统下垂控制策略通过模拟传统同步发电机的下垂特性，对逆变装置输出有功-频率、无功-电压进行独立解耦控制。但在微网实际运行过程中，存在线路阻抗分布不均匀、输出压降非线性等问题，这就会导致功率分配存在误差[7-8]。文献[9]通过改进下垂控制算法，使逆变装置输出阻抗在低频呈感性、高频呈阻性，实现频率无静差及电压小静差调节，但该改进算法需要微网内并网逆变器同时调节下垂系数，对时间同步系统要要求较高。文献[10]建立并网逆变器VSG模型，引入虚拟阻抗来实现均流，这增加了控制系统的复杂度，同时降低了输出电能质量。

为了提高微网逆变装置在无功补偿稳压调节过程中的抗干扰能力，使下垂控制系统具备全局鲁棒性。文献[11]在控制算法中加入虚拟惯量来提供系统的惯性支持，减少电压变化率，但并未考虑与下垂控制的配合；文献[12]提出一种基于滑模变结构的并网逆变器控制方案，将该方案应用电压外环PID控制中，但因为对控制参数较为敏感，响应效果一般。

本文首先建立并网逆变器线性下垂控制方程；然后针对传统下垂电压调节过程中存在分配误差且无功补偿增减幅度过大问题，提出一种改进下垂控制方案，通过引入电压补偿相和自适应下垂系数来增加电压分配精度和减少无功补偿范围；接着为了提高微网中逆变装置的抗干扰和动态性能，提出一种改进抗扰动观测器用来抑制电压波动，在抗扰动观测器中引入双扰动补偿相来抑制电压调节偏差问题；最后将上述控制策略通过Matlab∕Simulink仿真和实验来验证本文所提方案的有效性。

1 微网数学模型及传统下垂控制

1.1 微网双DG等效及逆变器模型

图1为包含两组DG的微网戴维南等效电路图。其中：U1∠δ1、U2∠δ2为第一、第二并网逆变器输出电压；U0∠0为负载阻抗两端电压；Z1=R1+jX1、Z2=R2+jX2，为第一、第二输电线路等效阻抗；Zload为负荷等效阻抗。

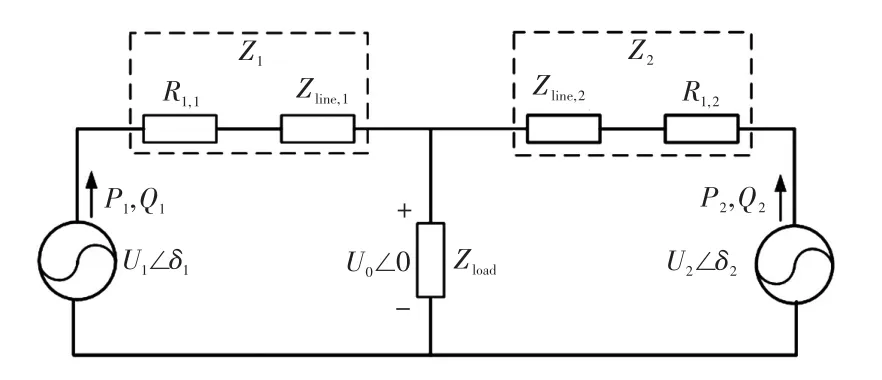
图1 双DG的微网戴维南等效电路Fig.1 Thevenin equivalent circuit of double-DG microgrid

根据图1的戴维南等效电路，单个DGi输出有功、无功功率可表示为

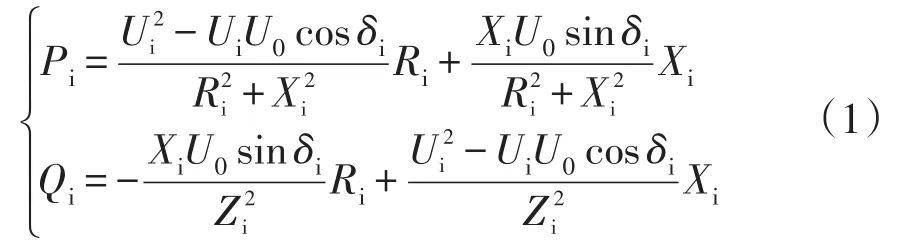
在微网中，输电线路阻抗呈阻性(Ri≫Xi,Ri≈Zi,Xi≈ 0 ，功角δi→0），即 sinδi≈δi，cosδi≈ 1，则上式可简化为

在实际微网系统中，各DG的逆变器参数不尽相同，输电线路阻抗存在参数漂移，采集存在误差，这将导致向负荷输送的功率不能按实际容量进行精确配比。微网中DG大多采用L型并网逆变器与输电线路相连，并网逆变器电路拓扑如图2所示。

图2 L型并网逆变器电路拓扑Fig.2 Topology of L-type grid-connected inverter circuit

图中：Udc为逆变器直流侧电压；Rf、Lf、Cf构成RLC滤波器；R0为负载线路等效阻抗；Uac、iac为逆变器交流侧电压、电流；e0、i0为负载侧电压、电流。L型并网逆变器交流动态方程可表示为

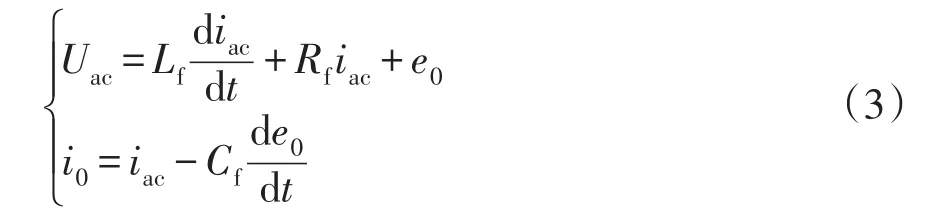
1.2 传统下垂补偿控制

由式（2）可知，微网单个DG逆变器输出有功功率与功角有关，输出无功功率与电压有关。为了实现并网逆变器电压调节，通过模拟同步发电机下垂外特性实现下垂无功补偿控制，控制方程为

式中：U是被控逆变器输出电压幅值；U0是空载输出电压幅值参考值；k是无功功率下垂系数；Q是负载分配的无功功率，传统的下垂控制是一种有差调节，根据式（4）可以得下垂无功补偿示意如图3所示。

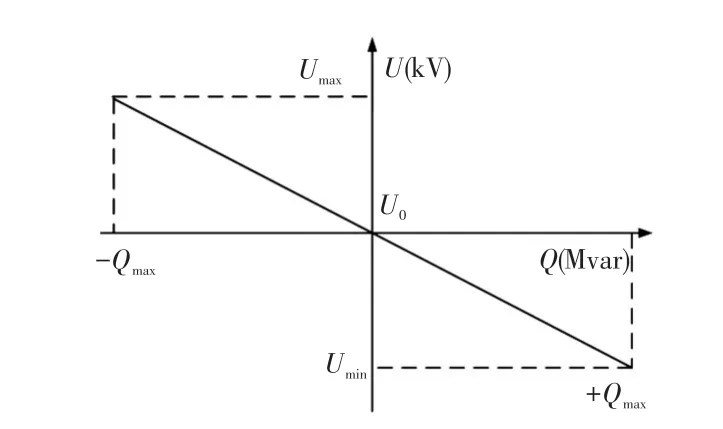
图3 下垂无功补偿示意Fig.3 Schematic of droop reactive power compensation

2 改进下垂无功补偿控制

2.1 改进电压补偿相

为改善下垂无功补偿控制效果，实现DG之间的无功合理分配，引入电压补偿相在下垂控制中，微网中DG输电线路产生的电压降可表示为

式中，ΔU是因为线路阻抗造成的电压降。本文提出一种对DG输电线路间存在的阻抗差值引起的压降进行补偿的方案，使各DG输电线路阻抗引起的压降一致。改进电压补偿可表示为

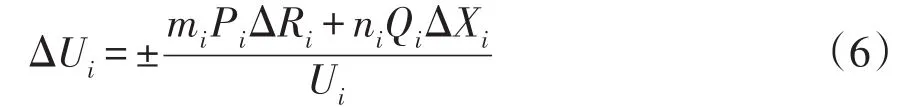
式中：ΔUi为DGi需要补偿的压降；ΔRi为第i条线路与基准线路间电阻差；ΔXi为电抗差；线路阻抗模值与基准线路阻抗模值相比较小时，补偿压降取负，反之为正。mi、ni为DGi有功、无功功率调节量一次函数相，可表示为：mi=-ai1ΔPi、ni=-ai2ΔQi。ai1、ai2分别为 DGi有功、无功相关系数；ΔPi、ΔQi分别为有功、无功改变量。

2.2 自适应下垂系数

传统下垂无功补偿控制中，下垂系数k为定值，无功补偿量与电压调节量成线性关系，但在微网实际系统中，一些电气设备对于电压波动较为敏感，当电压大范围调节时，极易造成设备脱网。本文提出一种自适应下垂控制方案，自动调节下垂系数来减少无功补偿范围，新型自适应下垂系数可表示为

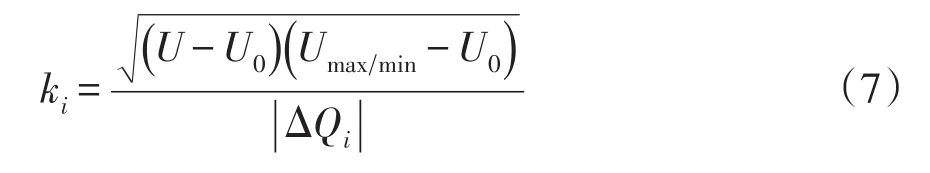
式中：ki为新型自适应下垂无功补偿系数；Umax、Umin为电压幅值的阈值上限、下限；其他与上式定义相同。当U-U0＞0，即调节电压为正时，分子系数选择Umax-U0；当U-U0≤0，即调节电压为负时，选择Umin-U0。将本文所提的自适应下垂系数带入下垂无功补偿控制中，可以得到如下图所示下垂控制曲线对比图。

在图4中，当面对U1→U2的电压调节目标，传统下垂无功补偿控制，因为是定下垂系数，无功调节量为ΔQ1。而采用本文所提的新型自适应下垂无功控制，自适应下垂无功补偿系数ki随着当前电压与目标电压差值变化而实时变化，面对同样电压调节目标，无功调节量为 ΔQ2（ΔQ2＜ΔQ1），无功补偿范围缩小，对系统影响更少。

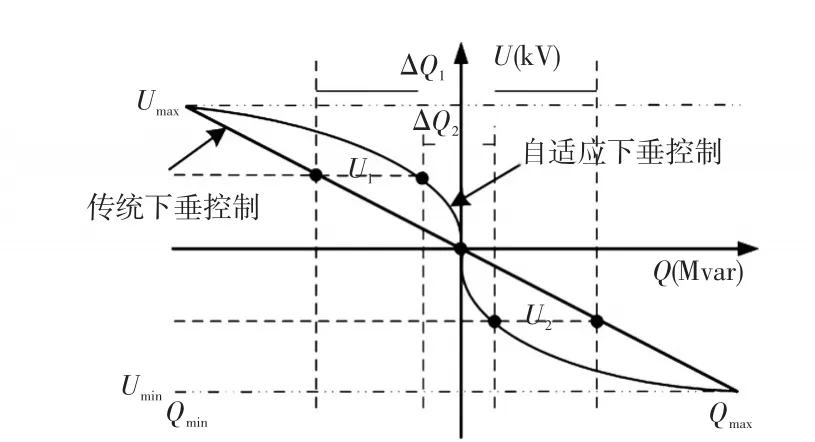
图4 下垂控制曲线对比Fig.4 Comparison between droop control curves

将改进电压补偿相ΔUi与自适应下垂系数ki带入电压下垂无功补偿控制中，得到新的控制方程为

3 抗扰动观测器

3.1 双扰动补偿相设计

为了将母线电压的波动有效抑制，本文提出一种双扰动补偿相，表达式为

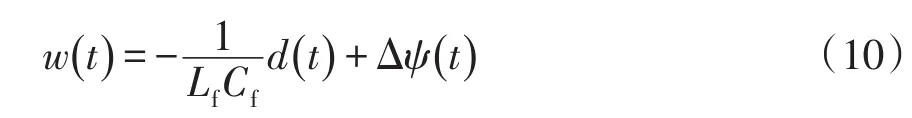
式中：d(t)表示由于DG负荷变化和出力调节引起的功率波动对电压动态响应的影响；Δψ(t)表示由系统参数不确定造成的电压分配偏差，表达式为

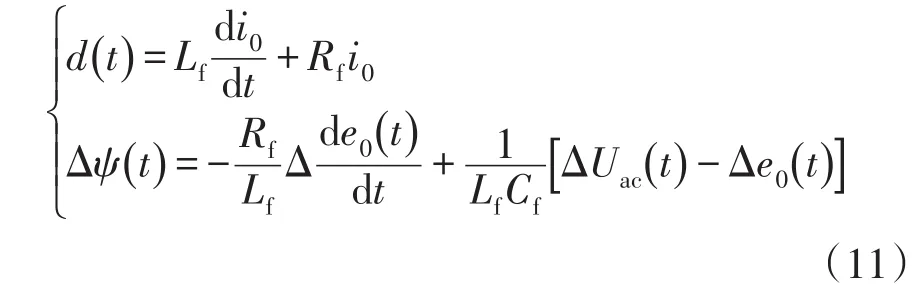
本文将扰动项d(t)与负载侧电流i0相关联，是因为逆变器输出电压响应滞后于电流变化，传统PI控制无法抑制因电流变化引起的母线电压暂态波动。在微网逆变器实际控制中，存在系统参数不确定等不利因素，这些误差项也会降低电压响应特性，所以本文在补偿扰动项中引入分配偏差补偿Δψ(t)。

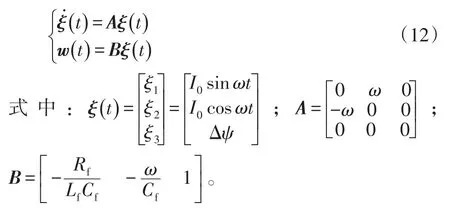
3.2 扰动观测器设计

扰动补偿误差动态方程可以表示为

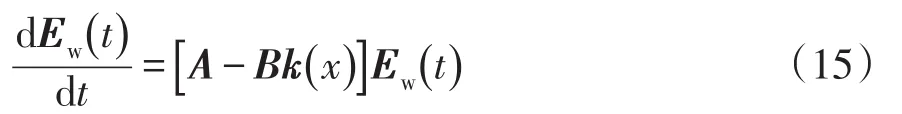
定义扰动补偿误差Lyapunov方程为

根据Lyapunov稳定判据可知：当V正定，负定时，系统在可渐进稳定至平衡点。则有：

将Ew和式（13）带入上式，可以得到：

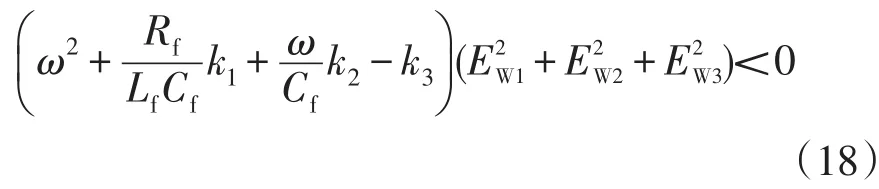
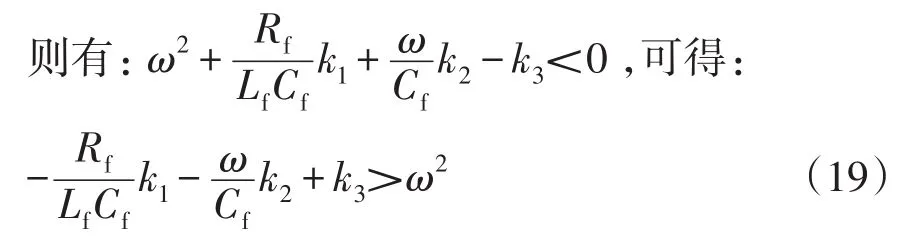
观测值增益k1、k2、k3选值需要考虑：观测器收敛速度和饱和效应影响，这就需要在一定范围内尽可能取较大的值。将本文所提扰动观测器输出电压作为参考信号，加入至电压控制环中，与改进电压补偿相ΔUi、自适应下垂调节相kiQi共同作用，提高微网无功补偿稳压调节性能。

4 Matlab/Simulink仿真分析

为了验证本文所提应用抗扰动观测器的微网改进下垂无功补偿技术方案的有效性。在Simulink下搭建如图5所示含有两个DG的微网仿真模型。

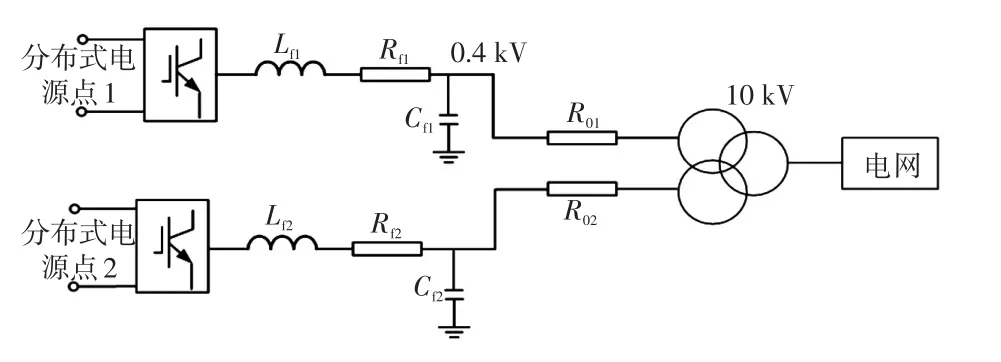
图5 含有两个分布式电源点的微网仿真模型Fig.5 Simulation model of microgrid with two DG points

DG1和DG2交流侧电压，与容量为1 000 kV·A的双绕组分裂式变压器相连，升压至10 kV后接入电网。两条输电线路RLC滤波参数相同，即：Lf1=Lf2=4.7 mH 、Rf1=Rf2=5 Ω 、Cf1=Cf2=490 μF ；线路阻抗R01=0.6+j0.15 Ω 、R02=0.3+j0.15 Ω 。系统控制参数为：有功下垂相关系数a1=1.5×10-5、无功下垂相关系数a2=1.2×10-5；无功下垂系数k=3×10-5；抗扰动观测器观测增益k1=-e-5、k2=75、k3=58。

为了验证所提改进下垂无功补偿控制性能，设定DG1和DG2逆变器容量比为2：1，仿真时间为1.2 s，在0.6 s时刻PCC发生增加负荷工况。增加负荷无功变化量为10.5 kvar。基于传统下垂无功补偿控制和改进下垂无功补偿控制得到的无功分配如图6所示，母线电压变化如图7所示。

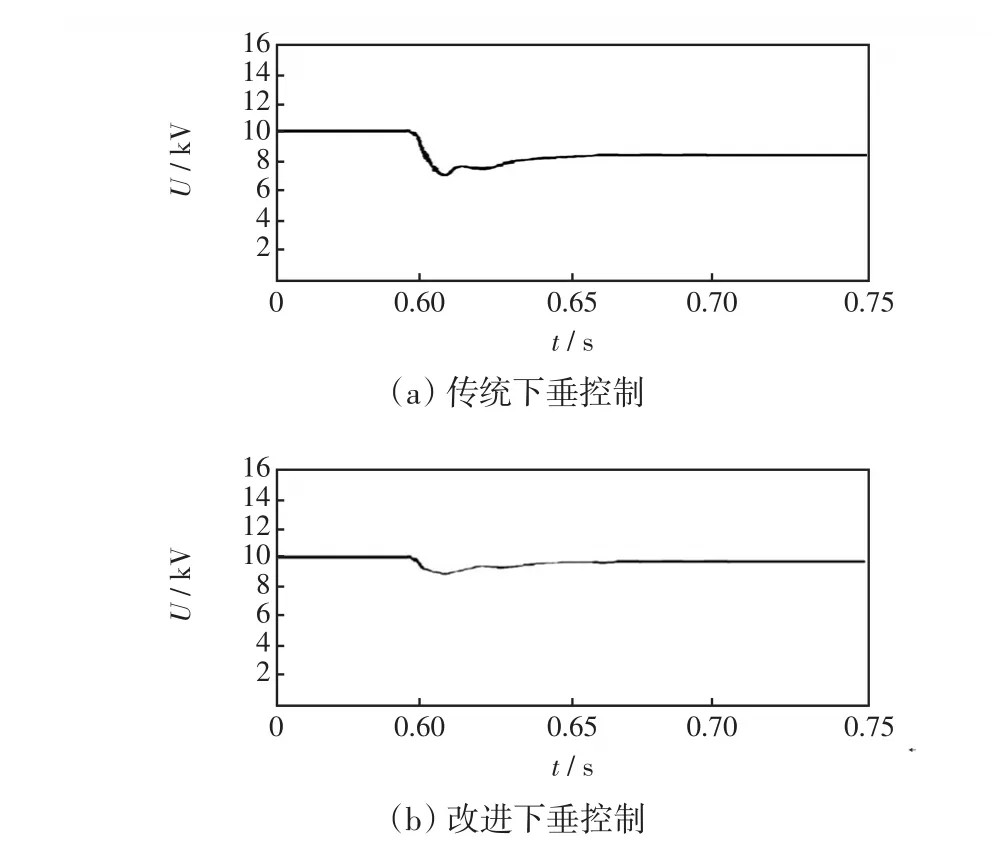
图7 系统无功增加母线电压变化仿真波形Fig.7 Simulation waveforms of bus voltage variation with increase in system reactive power

从图6（a）可以看出：0～0.6 s时间内，DG1输出无功功率为9.85 kVar，相对偏差为1.5%；DG2输出无功功率为7.52 kVar，相对偏差为50.4%。当在0.6 s时刻发生无功增量10.5 kVar负荷工况，DG1输出无功增加至14.21 kVar，增量为4.36 kVar；DG2输出无功增加至10.42 kVar，增量为2.90 kVar，并网点总增加负荷无功为7.26 kVar，偏差达到30.8%。

从图6（b）可以看出：0～0.6 s时间内，DG1输出无功功率为10.05 kVar，相对偏差为0.5%；DG2输出无功功率为5.03 kVar，相对偏差为0.3%。当在0.6 s时刻发生无功增量10.5 kVar负荷工况，DG1输出无功增加至17.26 kVar，增量为7.26 kVar；DG2输出无功增加至8.61 kVar，增量为3.58 kVar，并网点总增加负荷无功为10.84 kVar，偏差为3.2%，无功相对传统下垂无功补偿控制，分配偏差精度提高了10倍之多，保证了微网的供电可靠性，能更大程度上利用自身的容量，在短时间内有更多的无功来配合调节系统的功率不平衡。

从图7（a）可以看出：在0.6 s时刻PCC发生增加无功工况，经过0.07 s母线电压由10 kV下降至8.3 kV，稳态电压偏差较大且电压波动明显，最小下降到6.7 kV，极易造成一些电气设备因为欠压保护动作而停止运行。从图7（b）可以看出：在0.6 s面同样无功增加工况，经过0.04 s母线电压由10 kV恢复至9.9 kV，稳态电压偏差较小且电压波动较小，波动最小下降到8.8 kV，这是由于自适应算法减少了电压调节量，电压调节能够维持在设定的小偏移量范围内，消除了稳态电压偏差，提高了微网中分布式电源点的利用率。

为了验证所提改进抗扰动观测器可以有效抑制电压波动和电压调节偏差，设定仿真时间为1.2 s，母线电压参考初值为10 kV，0.4 s时DG1因事故切除，DG2单独运行0.4 s后母线电压存在0.2 kV电压波动，采用传统PI控制和含有改进抗扰动观测器控制得到的电压波形如图8所示，电压误差如图9所示。

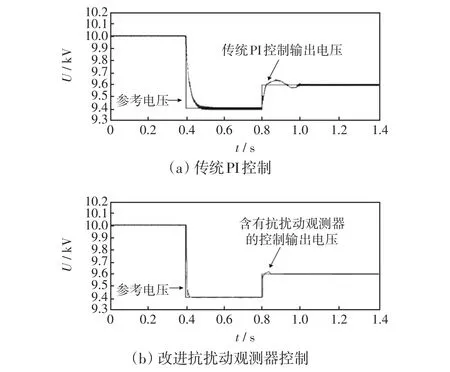
图8 母线电压变化动态仿真波形Fig.8 Dynamic simulation waveforms with bus voltage variation

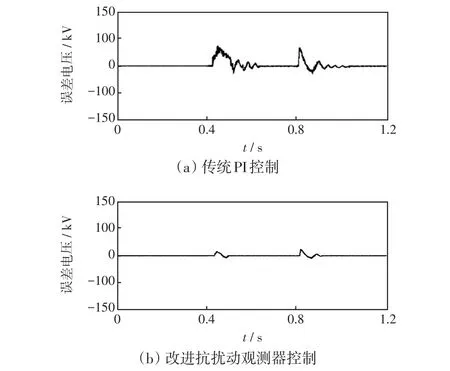
图9 母线电压调节误差仿真波形Fig.9 Simulation waveforms of bus voltage regulation error

从图8（a）可以看出：在0.4 s时刻，DG1因事故切除后，传统PI控制得到的母线电压延时0.06 s后下降至9.4 kV，存在响应滞后现象，且无法稳定在参考电压，存在调节偏差。在0.8 s时刻，面对0.2 kV电压波动，传统PI控制无法快速跟踪参考电压，且有20～80 V的超调量，波动较为严重，整个控制系统存在周期性延迟的问题。

从图8（b）可以看出：面对同样电源点切除，母线电压下降工况，采用本文提出的改进抗扰动观测器控制系统得到的响应电压波形，可以快速跟踪参考电压迅速调节至9.4 kV，不存在响应滞后问题，调节偏差得到了有效控制。在0.8 s时刻，面对同样0.2 kV电压波动工况，可以迅速响应调节，超调量也得到了很好的控制，具有更加快速和精确的电压调节能力，周期性延迟问题得到了很好的解决。

从图9（a）可以看出：在0.4 s时刻，面对母线电压下跌工况，传统PI控制存在较大调节误差，最大达到82 V，极易造成一些电气设备保护动作；在0.8 s时刻，当有0.2 kV电压波动，调节误差最大达到78 V且有电压震荡现象，整个控制系统稳态性能无法达到并网实际要求。从图9（b）可以看出：采用本文所提改进抗扰动观测器控制方法，可以有效减少调节误差，不管是面对因为电源点切除造成的电压跌落工况还是电压波动引起的系统震荡问题，控制系统都有较强的鲁棒性，电压误差可以控制在-5～10 V的范围内，提高了微网供电可靠性。

5 实验分析

为了验证本文所提控制方案的动态控制性能，搭建了含有两个并网逆变器的实验平台，实验平台硬件如下：DSP选择TI公司的TMS320F28335；IGBT选择Infineon公司的K40T120；示波器选择Tektro⁃nix公司的MDO4104B-3型示波器。实验参数与仿真参数类似。采用传统下垂无功补偿控制和本文所提改进下垂无功补偿控制得到的两台并网逆变器之间输出环流如图10所示。

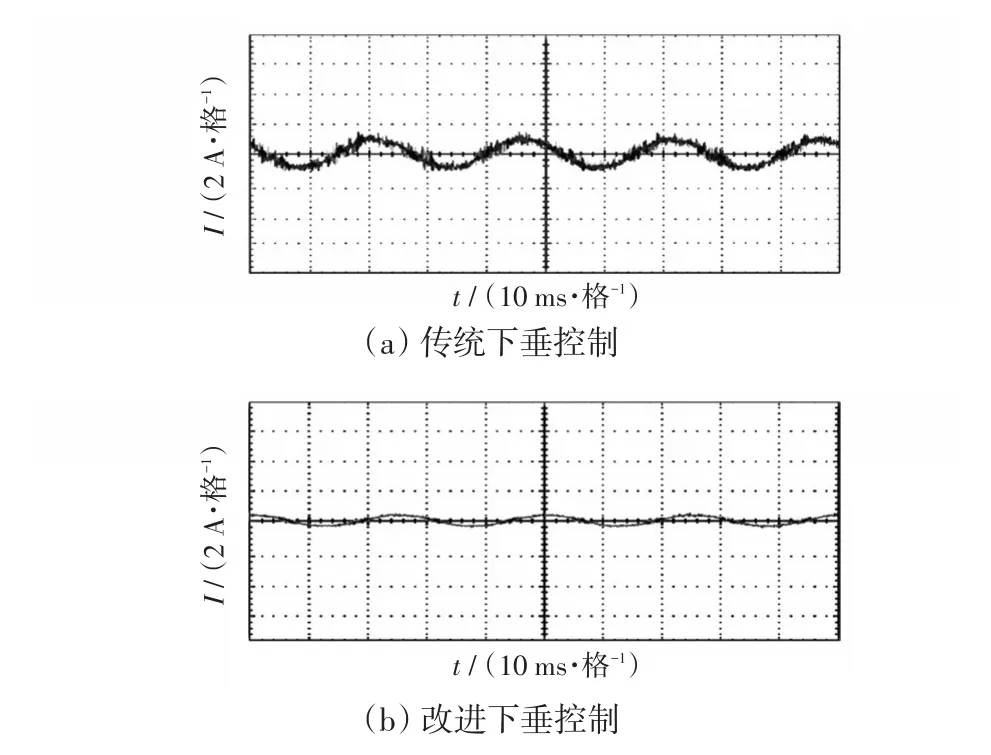
图10 并网逆变器之间输出环流实验波形Fig.10 Experimental waves of circulating current output between grid-connected inverters

输出环流大小可表征并网逆变器无功功率是否精确分配。对比图10（a）、（b）可知：采用传统下垂无功补偿控制输出环流较大，峰值达到1.8 A，而采样本文所提改进下垂无功补偿控制输出环流，峰值为0.19 A，环流抑制效果明显，可以实现无功功率精确分配的目标。当系统由满载突变为半载运行时，基于传统PI控制和本文所提改进抗扰动观测器控制策略下的单相电压动态波形如图11所示。

图11 满载突变为半载逆变器输出单相电压动态波形Fig.11 Dynamic waveforms of single-phase voltage output from inverter when full load is suddenly changed to half load

对比图11（a）、（b）可知：面对同样系统由满载突变为半载运行时，传统PI控制下的单相电压的调节时间为26.5 ms，采用本文所提改进抗扰动观测器控制调节时间为20 ms，动态调节时间更短，系统鲁棒性能高，周期性延迟问题得到了解决。采用本文所提控制算法的电压波形正弦稳定性能良好，峰值处纹波有效降低，系统抗扰动能力较强。

6 结语

本文针对传统下垂电压调节过程中存在分配误差且无功补偿增减幅度过大问题，提出一种改进下垂控制方案；为了提高微网中逆变装置的抗干扰和动态性能，提出一种改进抗扰动观测器用来抑制电压波动。

仿真和实验结果表明：本文所提改进下垂控制可以有效增加无功补偿分配精度，减少调节量，消除稳态电压偏差，环流抑制效果明显；所提改进抗扰动观测器控制可以有效提高微网暂态稳定性，增加控制系统鲁棒性，提高供电可靠性。本文所提方案具有一定的工程应用价值。