焊管生产线开卷机齿轮机构瞬态动力学分析*
杨佩东
(山西工程职业学院, 太原030009)
开卷机是焊管生产线的重要设备之一, 其主要作用是通过涨紧钢卷内孔来支撑住钢卷,并通过旋转将钢带头部送入矫平机中。 旋转运动主要是通过变频调速电机连接齿轮箱减速后驱动卷筒轴, 从而为开卷机提供动力。 齿轮机构在开卷机扭矩传递过程中有重要的作用, 它依靠轮齿齿廓直接接触来传递空间任意两轴间的运动和动力, 具有传递功率范围大、 传动效率高、 传动比准确、 使用寿命长、 工作可靠等优点, 在实际工程中得到了广泛应用。 开卷机齿轮箱在实际使用过程中, 齿轮经常会出现断齿、 齿面磨损、 齿面胶合等失效现象, 所以对开卷机齿轮机构进行瞬态动力学分析具有重要意义。
1 开卷机齿轮三维建模
目前工程上建立三维模型的软件有很多种,例如UG、 SolidWorks、 CATIA、 Pro/E 等。 齿轮三维模型的建立可以直接通过三维软件进行建模, 也可以通过齿轮插件GearTrax 进行建立,或利用专业齿轮设计软件KISSsoft 进行建模。本研究以某公司开卷机齿轮机构为研究对象, 采用SolidWorks 中Toolbox 插件进行建模, 只需输入齿轮相应的参数值, 软件便会自动生成相应的齿轮, 齿轮的基本参数见表1, 其中齿轮1 为从动轮, 齿轮2 为主动轮。
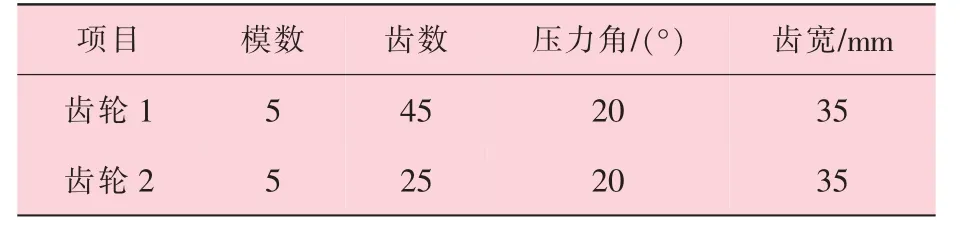
表1 开卷机齿轮的基本参数
一对渐开线齿轮正确啮合的条件是两轮的模数和压力角分别相等, 所以在建立齿轮三维模型时, 将其模数和压力角设为相同。 齿轮在啮合传动时, 为了避免一轮的齿顶与另一轮的齿槽底部以及齿根过渡曲线部分相抵触, 并留有一定空隙以便储存润滑油, 所以两齿轮在装配过程中, 一轮的齿顶圆与另一轮的齿根圆之间应当留有一定的间隙, 称为顶隙。 当顶隙为标准值时, 两齿轮的中心距依据公式(1) 进行确定[1]。

式中: a——齿轮中心距, mm;
r1、 r2——两轮分度圆半径, mm;
m——模数;
z1、 z2——两轮齿数。
通过公式 (1) 计算得出开卷机齿轮中心距为175 mm, 并在SolidWorks 装配模式下进行装配齿轮, 装配后的齿轮啮合三维模型如图1 所示。
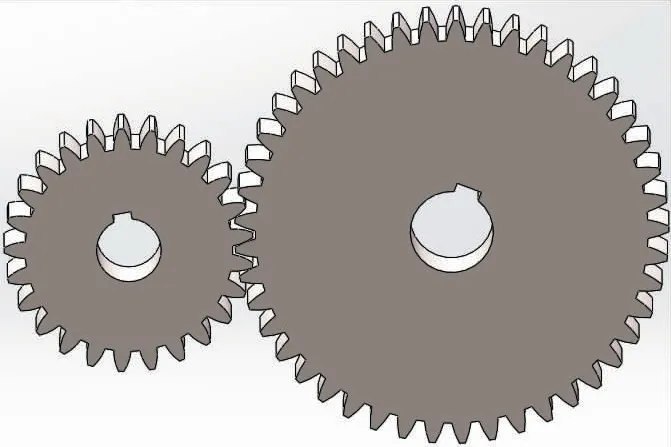
图1 齿轮啮合三维模型
2 齿轮瞬态动力学分析
2.1 瞬态动力学理论
瞬态动力学是用来分析结构在随时间任意变化的载荷作用下, 动力响应过程的技术。 在ANSYS Workbench 中, 使用Transient Structural模块进行瞬态动力学分析, 瞬态动力学的基本运动方程[2-3]为
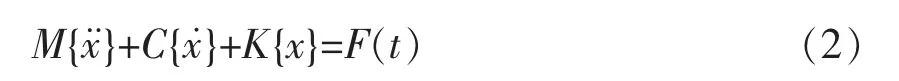
式中: M——质量矩阵;
C——阻尼矩阵;
K——刚度矩阵;
{x¨}——节点加速度向量;
{x˙}——点速度向量;
{x} ——节点位移向量。
2.2 材料性能
常见的齿轮失效形式有轮齿折断、 齿面磨损、 齿面点蚀以及塑性变形等。 为了避免齿轮失效, 对齿轮材料性能的基本要求为: 齿面要硬、齿芯要韧。 常用的齿轮材料有钢、 铸铁和非金属材料等, 由于钢材的韧性好, 耐冲击, 还可以通过热处理或化学热处理来改善其力学性能以及提高齿面硬度, 所以工程上通常使用钢材来制造齿轮。 本研究所采用的齿轮材料为45 钢, 其力学性能见表2。
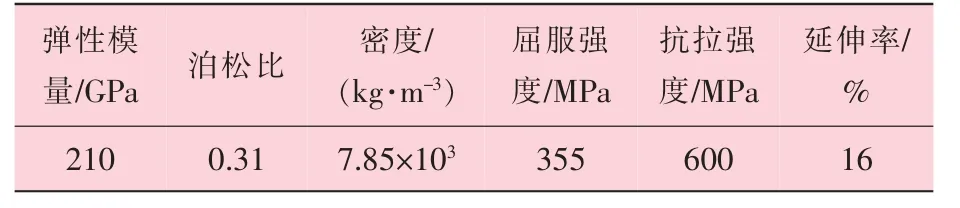
表2 45 钢的力学性能
2.3 网格划分
在ANSYS Workbench 中选择Mesh 模块对实体模型进行网格划分, 网格的结构和疏密程度将直接影响到计算结果的精度, 但是网格加密会增加计算机CPU 计算时间, 并需要更大的存储空间。 理想的网格划分, 是网格细化后, 求解结果不会发生明显的改变。 Mesh 模块会根据不同的物理场需求提供不同的网格划分方法, 常见的网格划分方法有: 自动网格划分 (Automatic)、 四面体网格划分 (Tetrahedrons)、 六面体主导网格划分(Hex Dominant)、 扫掠法(Sweep)、 多区法(Multizone)、 膨胀法(Inflation) 等[4-5]。 为了综合考虑计算精度与计算速度, 在划分网格时, 采用程序自动网格划分方法, 且网格单元尺寸设置为5 mm, 网格化的装配体模型如图2 所示, 其中网格单元数为17 703, 节点数为84 885。

图2 网格化的齿轮装配模型
2.4 边界条件及载荷约束
由于主动轮和从动轮齿数较多, 每个啮合齿面分别单独进行接触设置, 较为耗时。 为了快速准确地设置齿面接触, 使用Named Selection 方法设置齿轮接触。 齿轮啮合属于摩擦接触, 摩擦系数设置为0.1。 由于齿轮啮合时做旋转运动,所以对啮合的两个齿轮分别添加运动副joint:body-ground, 类型选择为转动副Revolute, 使齿轮沿着轴线进行旋转。 主动轮施加转动速度Rotational Velocity, 大小设置为30 r/min; 从动轮施加一个阻尼力矩Moment, 大小设置为600 N·m,且方向与从动轮转动方向相反。 在进行求解时,为了计算平稳, 打开大变形Large Deflection, 关闭弱弹簧Weak Springs。 为了确保一个完整的轮齿参与啮合, 求解时间设置为0.2 s, 初始子步设为200, 最小子步设为20, 最大子步设为30 000。施加边界条件及载荷约束如图3 所示。

图3 齿轮装配模型边界条件及载荷约束
2.5 计算结果及分析
通过对齿轮机构进行瞬态动力学分析, 得出齿轮啮合过程中Von Mises 等效应力云图、 最大等效应力局部放大图、 齿面接触状态云图、 齿面接触应力云图、 最大等效应变云图, 如图4所示。
从图4 (a) 和图4 (b) 可以看出, 最大等效应力出现在主动轮与从动轮刚接触啮合的位置上, 最大等效应力值为204 MPa。 齿轮材料的屈服强度σs为355 MPa, 齿轮在工作过程中不发生破坏的条件是其所受最大应力值σmax不超过许用应力[σ], 即σmax≤[σ]。 而许用应力[σ] =σs/s,当安全系数s 取1.5 时, 得出 [σ] =237 MPa,即齿轮的许用应力为237 MPa, 可知齿轮所受的最大等效应力小于其许用应力, 满足强度要求[6-8]。 从图4 (e) 可知, 在齿轮啮合传动过程中, 最大等效应变同样发生在主动轮与从动轮刚接触啮合的位置上, 最大等效应变仅为9.722 9×10-4mm,对齿轮影响较小。
图4 (c) 齿面接触状态云图中, 齿轮在啮合过程中无粘结现象, 表明齿轮在啮合传动过程中齿面的接触状态良好[9-10]。 图4 (d) 的齿面接触应力云图中, 最大接触应力出现在靠近节线的齿根面附近, 最大接触应力值为60.83 MPa,远小于齿轮的许用应力。 齿轮齿面最为常见的失效形式是点蚀, 其产生的原因是齿面在变化的接触应力作用下, 由于疲劳而产生麻点状损伤现象。 点蚀最先出现在靠近节线的齿根面上,然后再向其他部位扩展[11], 点蚀最先出现的位置与本次分析的齿面最大接触应力部位相同, 表明此次研究分析合理有效。
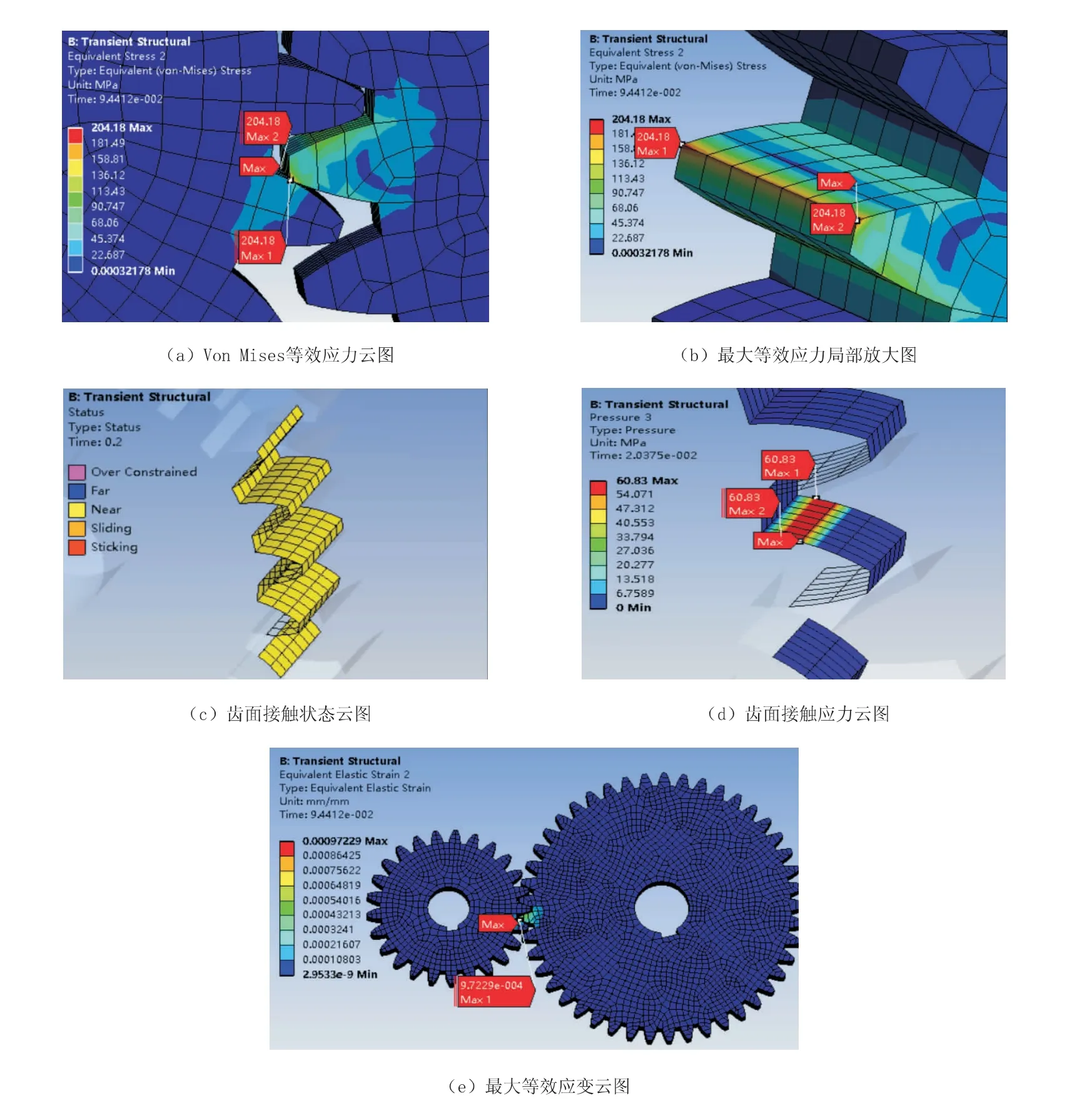
图4 齿轮机构瞬态动力学分析结果
通过对齿轮啮合过程中, 最大等效应力值随时间变化的数据进行统计后, 得出最大等效应力随时间变化曲线如图5 所示。 从图5 可以得出, 主动轮与从动轮刚接触啮合的时候, 所产生的等效应力最大, 应力值波动范围较大,最大值为204 MPa。 但随着时间的推移, 应力值趋向于稳定, 这是因为在开始啮合转动过程中, 由于主动轮具有一定的冲击力, 导致齿轮啮合产生的等效应力值较大, 但随着啮合的稳定进行, 齿轮啮合等效应力趋向于稳定。

图5 最大等效应力随时间变化曲线
3 结 论
(1) 在等效应力云图中, 最大等效应力出现在主动轮与从动轮刚接触啮合位置上, 最大等效应力值为204 MPa, 小于许用应力值, 满足强度使用要求。 在等效应变云图中, 最大应变值仅为9.722 9×10-4mm, 对齿轮影响较小。
(2) 在接触应力云图中, 最大接触应力值为60.83 MPa, 出现在靠近节线的齿根面附近,与齿轮通常最先出现点蚀位置相同。 在接触状态云图中, 齿轮啮合过程中无粘结现象, 表明齿面接触状态良好。
(3) 在最大等效应力随时间变化曲线中, 齿轮开始啮合时, 所受最大等效应力值较大, 但随着齿轮啮合的稳定运行, 齿轮啮合等效应力趋向稳定。

