广义对称表的矩阵象和点估计

白金峰，张应山，赵建立

(1.澳门城市大学 商学院，澳门 999078；2.华东师范大学 经济与管理学部统计学院，上海 200241；3.聊城大学 数学科学学院，山东 聊城 252059)

0 引言

对称性其实是一个非常古老的概念,对称性特性在自然界中既十分普遍又很重要，但同时它也是一个十分崭新的概念，因为自然界中几乎所有重要的规律都与某种对称性息息相关，所以人们可以通过研究对称性这一重要特性，去认识和研究自然规律。本文把在视觉感知特征方面具有对称形状和设计特性的事物作为对称性研究的主要研究对象，进行广义对称性相关方面的研究。对称性的概念解释是指对研究对象在视觉特征方面的形状和设计(张应山,赵建立,2018)。

对称性概念由来已久，主要有图像的对称和函数的对称两种，从最开始的视觉上的几何图形的对称性研究，再到现在抽象的函数的对称对称性研究，国内外已经有许多关于对称性理论方面的专著，即使这样，诸多研究学者还是对关于对称性理论方面的研究都充满着浓厚兴趣，趋之若鹜。在如今关于对称性方面的研究，大部分学者都将研究目光集中于图像的对称性和函数的对称性的研究上，其成果是硕果累累，而对称性的其他方面研究成果却寥寥无几。

目前所有的对称性研究都与有限群的研究成果密不可分，紧紧相连。譬如在图像的对称性的研究[1-7]方面，除了王佳利等(2015)[1]和顾振华(2009)[2]等人进行过关于群与图的对称性方面的研究之外,还有王志衡等(2017)研究过图的对称性检测[3]，图的容错性则成为杨大伟(2016)[4]和王牟江山(2014)[5]的主要研究目标，向德辉(2012)主要把有关图像分割及可视化作为研究方向[6]，周进鑫(2008)则对曲面嵌入等相关问题进行相关的研究[7]等。又譬如在函数的对称性的研究[8-14]方面的研究，Gordon James(2017)[8]，刘洋(2014)[9]，徐海静(2011)[10]，贺艳妮(2011)[11]，司华斌(2009)[12]等学者都进行了涉及有限群的特征标表等方面的研究[8-12]，他们在有限群的特征标表的研究方面都做出了取得了一定的研究成果，进一步完善了关于函数的对称性方面的研究，但也有一部分学者关于对称函数的特殊性质进行研究，如孙明保(2014)[13]及张映辉等(2017)[14]学者就对Schur凸性进行深入的研究。

张应山教授(1993)根据东方整体性思维和中国古典传统文化，并结合有限群等西方概念，提出了广义对称性或广义对称分析方法的相关概念[15]，他把以前狭义的有限群的特征标表做了进一步的推广和延伸，将其扩大成为《多边矩阵理论》中提到的正交幂等系统(对称算符表)和广义对称表的新形式，再利用统计分析等数学方法来进行对称函数方面的问题与性质的研究。在张应山教授(1993)提出关于对称框架和对称算符理论的相关概念[15]以后，张应山等(1998)根据对称框架和对称算符理论的相关概念，对正交幂等系统进行相应的研究，提出了饱和正交幂等系统的概念[16]。潘长缘,张应山(2008)等人提出了关于如何构造正交幂等系统的一种算法，继续进行关于饱和正交幂等系统的构造的研究[17]，这些为之后研究广义对称性打下一定的基础。陈雪平，张应山(2009)等人还继续了其他广义对称性相关概念的研究，这些研究对象主要是多元函数空间的对称性分解方面的概念[18]，其研究成果会进一步丰富对称性问题的研究成果，为之后的广义对称性研究提供支持。在关于对称性全局统计分析中的定理证明的研究方面，潘长缘,马海南(2009) 等人证明了对称性全局统计分析方法中的几个重要定理[19]，罗纯，张应山(2016)利用高维模型表示方差分析的对称全局灵敏度分析，进行了相关定理的证明，这些构成了对称性全局统计分析方法的核心基石[20]，可以有助于进一步深化广义对称性的研究。在处理复杂系统的新思维系列论文[21-27]中，罗纯和张应山等教授提出了对称框架的剖分定理、对称框架的分解定理，并利用该定理提出了构造对称框架的一种方法，如此等等，对广义对称性的研究有着重要意义。钱洪岗(2012)[28]和刘兴虎(2012)[29]在对称设计表的构造和数据分析方面的问题上，两者都作了充分的进一步探讨和研究，钱洪岗(2012)通过介绍对称群理论，给出了对称框架的定义和相关性质,验证对称设计在解决具有高阶交互效应的试验设计问题上比正交设计具有更好的解决能力[28]。刘兴虎(2012)通过引出数据分析的三项基本原则，利用群论的相关概念和结论，引入了导出框架和对称框架的定义,还给出了对称框架关于群的相关理论概念。他们的研究让对称设计表方面的研究得到一定发展。不过上述提到的一系列关于对称性方面的研究成果大多都只限于对称表的研究，还没有真正涉及广义对称表的研究，诸多学者的研究都在为广义对称表的研究构筑框架，奠定基础。

基于张应山教授《多边矩阵理论》(1993)的概念理论[15]，结合文献《广义对称表的定义和哲学意义》(张应山，赵建立，2018)的研究成果[30]，对广义对称性进行进一步的探讨研究。作为广义对称表的系列论文之一，其主要目的是让具有再现性的广义对称表可以成为数据分析表，而该数据分析表便是用来解决函数对称分解问题的，这种研究有利于广义对称表在实际问题上的使用，具有很高的市场价值和实用价值。广义对称表的矩阵象是象数学的概念。它主要关注广义对称表的对称分解项的二次型相应的矩阵。这个矩阵具有换行换列换数码符号保持广义对称表的设计特性不变的性质。这使得广义对称表的对称矩阵象的数据分析结论具有再现性(定理1)。

广义对称表的点估计包含对于广义对称表的对称分解项及其方差和贡献率的估计。在试验设计理论中，这种估计是最基本的。对这些估计的了解，有助于以后模拟研究广义对称表的对称矩阵象的数据分析结论是否具有实际的再现性。文献《广义对称表的定义和哲学意义》(张应山,赵建立,2018)研究了广义对称表的定义和哲学意义[30],本文中主要是在上述文献的基础上计算广义对称表的矩阵象，并给出对称分解项及其方差和贡献率的点估计。最后，讨论广义对称表的矩阵象的哲学意义。

1 广义对称表的矩阵象

文献《广义对称表的定义和哲学意义》(张应山，赵建立，2018)研究了广义对称表的定义和哲学意义，并给出了广义对称表的定义，把广义对称表的概念得到标准化，又详细阐明了对称置换平衡性的概念[30]，这又为以后广义对称表的研究提供了平衡指标，所以这一篇文献[30]作为广义对称表系列论文的开篇之作，对以后的广义对称表的研究具有指导意义，为后面关于广义对称表问题的研究提供了非常大的帮助。

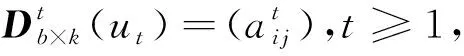
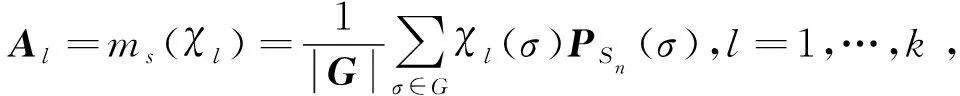
设根据多元函数f(x0,x1,…,xm,ω)的试验数据为Y， 那么

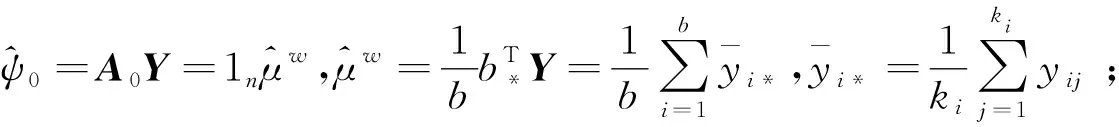
ψ1的最小二乘估计为

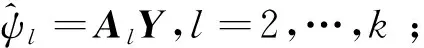
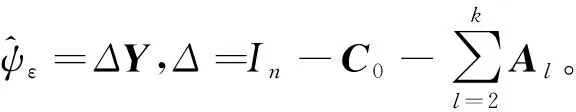
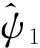
定理1广义对称表

基于其对称矩阵象的数据分析结论具有再现性。

证明需要论证广义对称表是解决对称分解问题的最基本设计，就是要证明利用对称矩阵象得到的数据分析结论具有再现性。也就是说：在对称分解项已知时，利用任何一个具有可识别性的广义对称表获得的数据，其数据分析结论与对称分解项的值基本保持一致，俗称客观一致性。在对称分解项未知时，利用不同的两个具有可识别性的广义对称表两次获得的数据，如果这两次数据分析结论都基本上相一致，两次分析结论可以重复出现，则这种性质称之为重复出现性。那么数据分析结论必须同时具有客观一致性和重复出现性，这两种性质必须同时成立，只有这样才能说明数据分析结论具有再现性；否则便不能说明数据分析结论具有再现性，因此才说再现性是客观一致性和重复出现性的统称[30]。

水平数相同的不同的广义对称表主要表现在对称表的行号不同、对称表的列号不同、对称表的数码不同。因为基于广义对称表的试验设计数据分析结论都是基于广义对称表的矩阵象进行分析的，所以，要证明广义对称表具有再现性，就是要证明在换行换列换数码符号大小的条件下，广义对称表的矩阵象具有不变的性质。

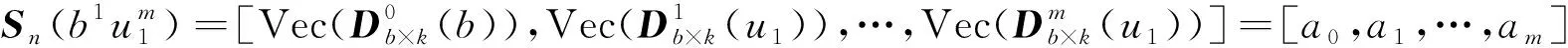
的对称置换不变性的要求对于试验的对称分析来说是最基本的。

关于对称分解项ψl的方差Var(ψl)的估计，可以采用对称矩阵象的试验数据Y的二次型来估计，因为对称矩阵象具有换行换列换数码符号不变的性质，所以基于对称矩阵象的点估计自然具有相同性质，即具有再现性。关于其估计的无偏和方差最小性质，利用投影矩阵性质也比较容易证明。类似地考虑贡献率及其误差方差的无偏、方差最小和再现性。

2 广义对称表的矩阵象构造

构造广义对称表的矩阵象的方法有很多，本文给出一种利用多边矩阵的置换矩阵[15]构造广义对称表的矩阵象的一种方法。

例1 考虑如下形式的广义对称表(S4(2133);G)，其中G={e,σ,σ2},σ=(1 2 3)∈S3，

相应的区组设计为

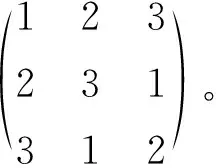
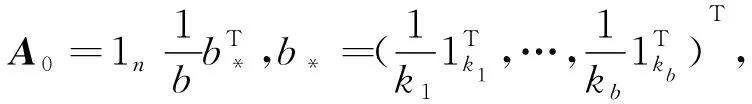
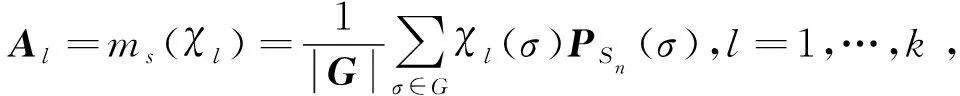
Δ=I4-C0-A2=04×4。

对于广义对称表(S4(2133);G)的试验数据Y=(y11;y21,y22,y23)T，ψl的最小二乘估计为

广义对称表(S4(21;33),G)的方差Var(ψl)的估计为

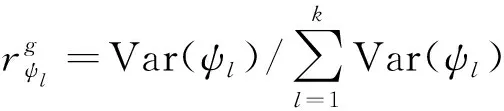
注意：关于因子x0的水平估计、方差和贡献率同于对称算符χ1≡1的水平估计、方差和贡献率。

例2 考虑如下形式的广义对称表(S4(2123);G)，其中G={e,σ,σ2},σ=(1 2 3)∈S3，

相应的区组设计为

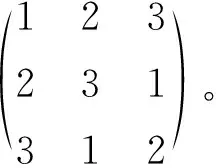
便是这个群所拥有两个饱和正交幂等系统其中的一个形式。计算

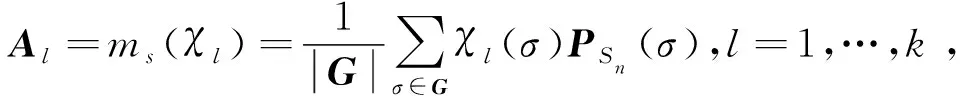
Δ=I4-C0-A2-A3=04×4。

对于广义对称表(S4(2123);G)的试验数据Y=(y11;y21,y22,y23)T，ψl的最小二乘估计为

广义对称表(S4(21;23),G)的方差Var(ψt)的估计为

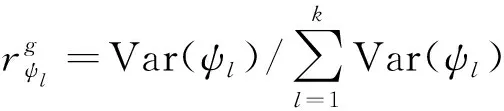
注意：关于因子x0的水平估计、方差和贡献率同于对称算符χ1≡1的水平估计、方差和贡献率。

例3考虑如下形式的广义对称表(S9(3134);G)，其中子群G={e,(1234),(13)(24),(1432)}⊂S4。

相应的区组设计为

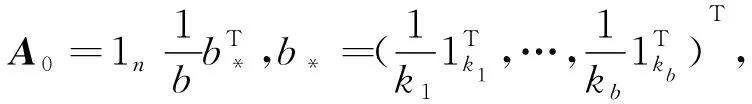
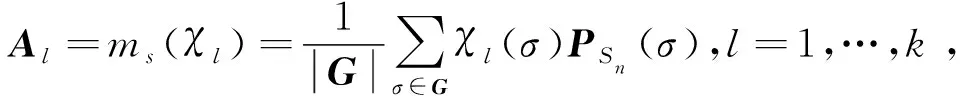
Δ=I9-C0-A2=09×9。

对于广义对称表(S9(3134);G)的试验数据Y=(y11;y21,y22,y23,y24;y31,y32,y33,y34)T，ψl的最小二乘估计为

广义对称表(S9(3134);G)的方差Var(ψt)的估计为

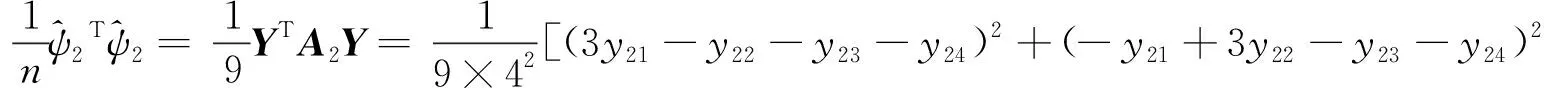
+(-y21-y22+3y23-y24)2+(-y21-y22-y23+3y24)2+(3y31-y32-y33-y34)2

+(-y31+3y32-y33-y34)2+(-y31-y32+3y33-y34)2+(-y31-y32-y33+3y34)2]。

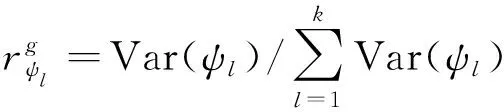
注意：关于因子x0的水平估计、方差和贡献率同于对称算符χ1≡1的水平估计、方差和贡献率。

3 广义对称表矩阵象的哲学意义

在试验设计领域，关于设计表的平衡性和正交性定义非常之多，哪种平衡性和正交性的定义更合理？也是争论不休。而试验设计要解决的最终问题是对自由函数模型(1)的观测函数的正交或者对称分解项进行正确估计，其估计结论应不受对广义正交表或者广义对称表选择的影响。

张应山教授(2018)提出了关于正交分解具有五种平衡性的概念，即正交分解具有相遇平衡性、水平间平衡性、正交平衡性、水平内平衡性和整体平衡性[31]。这五种平衡性的概念是张应山教授根据中国传统的“阴阳五行”理论作为基础，结合东方整体思维模式，创造性提来的多边矩阵理论的一部分理论应用[31]。于此同时通过研究证明了广义正交表具有相遇平衡性和正交平衡性的特性，所以广义正交表就能够成为解决正交分解问题的最基本设计。广义正交表可以保证其矩阵象具有正交性，因此通过使用广义正交表的方式获得的试验数据，在基于广义正交表的矩阵象的条件下进行数据分析，其得到的结论同时具有客观一致性和重复出现性，也就是结论具有再现性。

关于对称分解来讲，其平衡性只具有一种：对称置换不变性[30]。本文证明了只要广义对称表具有对称置换不变性，那么广义对称表就是解决对称分解问题的最基本设计。在正交幂等系统的帮助下，它可以保证其对称矩阵象具有正交性。因而利用广义对称表获得的试验数据，基于广义对称表的矩阵象进行数据分析，其数据分析结论具有再现性。

4 结论

本文提出了广义对称表的矩阵象定义，阐述了根据对称矩阵象，其得的数据分析结论是有再现性的结论性概念，同时给出了一种构造方法。这种构造方法对之前文献提出的广义对称表构造法的进一步延伸，是关于广义对称表矩阵象的构造方法。又因为广义对称表矩阵象的概念与中国古典传统文化中的象数学概念同根同源，双方有着密不可分的联系，所以对广义对称表矩阵象问题的研究，其实也是对中国古典传统文化的象数学问题进行一定的研究，两者相辅相成，可以相互促进各自研究的发展，相互借鉴其研究成果。因而，本系列论文是以研究广义对称表矩阵象理论的推广和实际应用作为研究的重要目的，对关于广义对称表方面的问题进行一系列的研究分析，着力推动广义对称表相关的理论和成果的应用。