FINFLO：快速局部异常点检测算法

杨校林，李菁菁，李易

1.中国科学院计算机网络信息中心，北京 100190

2.中国科学院大学，北京 100049

引言

Hawkins 对离群点的本质做如下定义：离群点是数据集中偏离大部分数据的数据，由于偏离其它数据太多，使人怀疑这些数据的偏离并非由随机因素产生，而是产生于完全不同的机制[1]。离群点检测是数据挖掘领域中的一项重要技术，目的是在大量且复杂的数据集中剔除噪音并保留有意义的数据点。离群点检测被广泛应用在网络监控、金融欺诈、数据清洗、电子商务、故障检测、天气预报、医药研究、信用贷款等众多领域。迄今为止，众多科研人员已经提出很多的离群点检测相关算法，大致分为如下四类：基于统计模型、基于距离模型、基于密度模型和基于偏离模型[2]。随着人工智能和模式识别的兴起，越来越多新颖的算法被提出，越来越多的应用被落实[3]，例如，基于模糊粗糙集的离群点检测算法[4]和利用自组织映射离群点检测技术[5]，文献[6]提出了一种基于深度信念网络的多类支持向量机入侵检测方法，该方法可以有效缩短分类器的训练时间，同时提高入侵异常点的分类准确率，文献[7]将迁移学习应用在时序数据离群点检测并取得了良好的结果，Rivero等人[8]应用决策树获取元数据，然后将新网络攻击类别映射为高斯流型中的数据对象，计算新类别与已知类别之间的距离，该方法可以很好的检测出新的网络攻击类别。

基于统计模型的算法要求知道关于数据集合参数的知识，比如数据分布，但是在大多数情况下数据分布是未知的。为了改进基于统计模型算法的缺陷，科研人员引进了基于距离的异常检测算法，这种算法可以不需要预先知道数据的分布模式，也可以很好的适应高维度数据集，但是基于距离的异常点检测算法只能发现全局的异常对象，无法发现局部的异常对象， 同时有科研人员引进分布式计算方式加速异常点检测的计算[9]。Breunig 等人在 2000年提出了基于局部密度的离群点检测算法 LOF[10]，LOF 算法基于每个对象和它的k-近邻对象的局部可达密度计算局部异常因子，并将局部异常因子与自然数1 比较，大于1 可能是异常数据点，小于1 则是正常点。Jin W.等人提出了INFLO 算法[11]，该算法在计算对象的局部异常因子时同时考虑了对象的k-近邻对象和反向k-近邻对象，从而避免了算法对分布在簇边缘的对象的误判。但是INFLO 算法的时间复杂度很高，需要频繁查找对象的反向k-近邻对象。除此之外，还出现了很多借鉴LOF 算法思想计算局部异常度的度量方法，比较典型的有计算基于连接的异常系数的COF 算法[12]，局部空间异常测度SLOM 算法[13]和基于局部信息熵的加权子空间离群点检测算法[14]。基于偏离模型的算法也借鉴了基于局部密度的LOF 算法，有多粒度偏差系数MDEF 算法[15]等。这些算法的时间复杂度高，算法的精确度依赖用户指定的参数。岳峰等于2007年提出基于反向k-近邻的孤立点检测算法ODRKNN[16]，该算法认为数据点的反向K 近邻个数越少，说明它的偏离程度越大，数据点越有可能是一个异常点，但是该算法在数据量大且维度高的情况下，算法就会出现误差。

本文改进了INFLO 算法，提出了一种基于局部密度的快速异常点算法FINFLO，因为数据对象的k-近邻对象和反向k-近邻对象不是对称的，频繁计算数据对象的反向k-近邻对象是非常耗时的。所以本文算法计算对象的局部异常因子时在符合给定条件时不会同时考虑对象的k-近邻对象和反向k-近邻对象，由此计算出来的数据对象的局部异常因子仍然可以高效地定位局部异常对象，且效率大大提升。并且在多簇环境下，该算法的精确度并没有降低，仍然可以适应于多簇环境中。

1 预备知识

1.1 LOF 算法

Breunig 等人在 2000年提出了基于局部密度的离群点检测算法 LOF，该算法会计算出对象的局部异常因子表征对象的离群程度，不是二值性表示，而是一种趋向性表示。

LOF 算法通过比较每个对象p 和其k-邻域对象的密度来判断该对象是否为异常，这样允许出现对象分布不均匀、密度不同的情况。对象p 的局部密度越低，越有可能是异常点。即若对象p（距离其他对象偏离较远，其k-邻域内邻居大多数对象的局部可达密度相对较大，对象p 的局部可达密度相对较小，计算得出对象的局部异常因子较大。算法中的基本定义如下：

定义1（k-邻近距离 k-distance）：在距离对象p最近的几个对象中，第 k 个最近的对象o 与对象p 之间的距离称为对象p 的k-邻近距离，记为k-distance(p)，其中对象o 满足以下条件：

（1）至少存在k个对象使得

（2）至少存在k-1 个对象使得

定义2（可达距离 reachability distance）：可达距离的定义和k-邻近距离是相关的，给定参数k时，对象p 相对于对象o 的可达距离reach-distance（p,o）为对象o 的k-邻近距离和对象p 与对象o 之间的直接距离的最大值。即：

定义3（局部可达密度 local reachability density）：对象p 的局部可达密度为它与邻近的对象的平均可达距离之和的倒数，即：

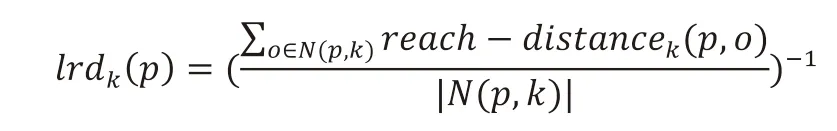
定义4（局部异常因子 local outlier factor）：局部异常因子是用局部相对密度来定义的。对象p 的局部相对密度（局部异常因子）为对象p 的k-近邻的平均局部可达密度跟数据点p 的局部可达密度的比值，即：

1.2 INFLO 算法

LOF 算法仅仅适用于单簇数据分布环境，对多簇数据判定时极易出现误判。Jin W.等人针对LOF算法的缺陷，提出了INFLO 算法， INFO 算法计算对象的局部异常因子时不仅仅考虑了对象的k-近邻对象，还考虑了对象的反向k-近邻对象。同时，INFLO 算法计算得出的局部异常因子也是一种趋向性表示。

INFLO 算法计算对象局部因子的方法同LOF算法一致，但是在对象分布存在两簇甚至多簇时，INFLO 算法的性能明显优于LOF 算法。FINFLO 算法计算对象的局部异常因子时同时考虑其k-近邻对象和反向k-近邻对象。如果对象是处于簇边缘的正常对象，它必然处于其他对象的k-近邻对象域中，因此其局部异常因子也会置于正常范围之内，也即小于1 或接近于1。该算法的基本定义如下：

定义1（局部密度 local outlier density）：对象p的局部密度为其k-邻近距离的倒数，即：

其中k-邻近距离同2.1 LOF 算法中的定义1。

定义2（反向k-近邻 reverse KNN）：若对象q 的k-近邻中包含对象p，则对象p 的反向k-近邻中包含对象q，即：

定义3（影响域离群因子influenced outlierness）：对象p 的影响域由其k-近邻和反向k-近邻组成，对象p 的影响域异常因子为其影响域内对象的平均密度和它的局部密度的比值，即：

其中：

2 FINFLO 算法

2.1 算法思想

LOF 算法计算对象的局部异常因子时只考虑了k-近邻对象，当对象分布存在两个及以上簇时，LOF 算法容易将处于簇边缘的正常对象误判成异常。INFLO 算法引进了对象的反向k-近邻对象来解决LOF 算法的缺陷，但是此时算法在检索对象的反向k-近邻和计算局部异常因子时变得非常耗时。在现实生活中，数据对象分布中只有少量对象是分布异常，大多数的对象都是正常分布，且大多数对象都处于簇的内部，所以在计算对象的局部异常因子时，只有少量的对象才需要同时考虑k-近邻对象和反向k-近邻对象，这类对象一般分布在簇的边缘。FINFLO 算法在不影响算法准确率的情况下，重新设计数据对象异常判定策略，尽量减少考虑数据对象的k-近邻的对象。

2.2 基本概念

FINFLO 算法在计算对象的局部异常因子时，如果对象的反向k-近邻对象个数不小于所有对象的反向k-近邻对象个数的均值，则仅需要考虑k-近邻对象，否则需要同时考虑反向k-近邻对象。FINFLO算法的基本定义如下：

定义1（局部密度 local outlier density）：对象p的局部密度由两部分组成，一部分是其k-邻近距离的倒数，第二部分是底数为e，指数为负的k-邻近距离的指数：

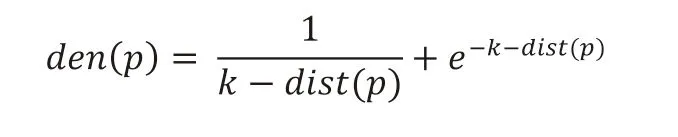
定义2（局部质心因子 local centroid factor）：对象p 的局部质心因子表征该对象的局部正常程度：

定义3（局部异常因子 local outlier factor）：对象p 的局部异常因子采用如下公式：

其中：

2.3 离群点判定策略

首先根据定义2 判定数据对象的局部质心因子，如果该数据对象的局部质心因子大于等于1，说明它是其k-邻域的局部质心，其k-邻域的所有数据对象可以以它为中心点形成一个点簇，它位于该簇数据点最密集的地方，所以它一定不是局部异常点。同时，根据定义3 计算局部异常值的计算方式，该点的局部异常值也一定会小于1。通过定义2 可以找出所有的局部质心点，局部质心点一定是局部正常点，可以避免后续判定。

如果数据对象的局部质心因子小于1，则不能认定该数据对象是局部正常点，需要进一步判定。根据反向k-近邻的定义，反向k-近邻与k-近邻并不是对称的，如果数据对象的反向k-近邻对象个数大于等于全局反向k 近邻对象个数的均值，在计算局部异常因子时，不需要考虑数据对象的反向k-近邻，这是因为在多簇数据分布的环境下，大部分数据分布在簇内部，只有少量的数据分布在簇的边缘，计算簇内部数据对象的局部异常因子时不需要考虑其反向k-近邻，而簇边缘数据对象的反向k-近邻一定比簇内部的反向k-近邻对象数量少，所以，本算法取全局反向k-近邻对象数目均值作为阈值边界，避免外部经验值输入。

如果数据对象的反向k-近邻个数小于全局对象反向k-近邻数目均值，则必须同时考虑该数据对象的k-近邻对象和反向k-近邻对象。

具体的伪代码描述如下：

Algorithm FINFLO:Input:k,D,a threshold T Output:label of p in D Method:1.FOR each p in D DO 2.Get its lcf based definition 2 on ；3.IF lcf ＞ 1 THEN 4.Label as a normal point;5.ELSE 6.N = getRKNN(p);7.IF N ＞ avg(RKNN) THEN 8.Get its lof based on definition 3;// not consider its RNN;10. IF lof ＞ = T THEN 11. label p as an outlier;12. ELSE label p as a normal point;13.ELSE 14. Get its lof based on defintion 3;15. // must consider its RNN;16. IF lof ＞ = T THEN 17. label p as an outlier;18. ELSE label p as a normal point;19.ENDFOR

3 实验分析

本节设计实验对LOF 算法，INFLO 算法以及FINFLO 算法的执行效率和检测精准度进行分析。测试的硬件环境是CPU 1.8GHZ，主存8G，软件环境为：操作系统Microsoft Windows 10，编程语言为Python 3。测试所使用的数据集为KDD CUP 1999 数据集，KDD CUP 1999 数据集使用的是DARPA 1998的原始数据，在DARPA 1998 数据集的基础上进行了预处理，提取出了以“连接”为单位的每条记录。KDD CUP 1999 数据集中的数据有40 个属性，取其中的20 个属性，具体为取9 种TCP 连接基本特征，9 种基于时间的网络流量统计特征和2 种TCP 连接的内容特征，对其中的非数值性属性进行了数值化处理，对连续型属性进行离散化处理。其中每一条数据记录都是一条网络连接，每条网络连接被标记为正常连接或者异常连接，异常类型被分为4 大类，共39 种攻击类型。在所有数据集中，异常数据占全部数据的2%～3%。

3.1 FINFLO 算法的精确度和执行效率

为了对比LOF 算法，INFLO 算法和FINFLO 算法的精确度和执行效率设计对比试验， 将KDD CUP 1999 数据集作为实验数据集，评价算法性能的指标为真正的异常点占算法结果中返回的异常点的比值，比值越大，则算法的性能越好；同时算法的执行时间作为执行效率的指标，时间越短，算法的执行效率越高。算法的精确度公式为：

KDD CUP-500 数据中含有数据记录500 条，维度为20，KDD CUP-1000 数据集中含有数据记录1,000 条，维度为20， KDD CUP-2000 数据集中含有数据记录2,000 条，维度为20。三组实验的结果如图1 和图2所示，可以看出在每一组实验中，LOF的算法执行时间最长，FINFLO 算法的执行时间最短，同时 INFLO 算法结果的准确率和FINFLO 算法的准确率是一样的，也是最高的。这是因为在LOF 算法中计算数据对象的k-可达距离计算复杂，进而导致了数据对象局部密度计算耗时，同比之下INFLO 算法和FINFLO 算法在没有折损精度的情况下改进了数据对象局部密度的计算方式；同时可以看出，相比于INFLO 算法，FINFLO 算法在没有牺牲准确率的情况下，运行时间大大缩减，这是因为FINFLO算法计算数据点的局部异常因子时首先进行了剪枝操作，质心因子大于1 的数据对象必然不是异常对象，同时符合条件的数据对象在计算局部异常因子时不会考虑反向k-近邻，这是因为KNN和反向KNN是不对称，如果一个数据对象处于高密集区域，该数据对象的反向KNN 集合则非常大，计算时非常耗时且无用。

图1 三种算法的准确率对比图Fig.1 Comparison of precision of three algorithms

图2 三种算法的运行时间对比图Fig.2 Comparison of runtime of three algorithms

3.2 FINFLO 算法的优化测试

在不同规模的数据集上设计实验，设置不同的K 值测试FINFLO 算法的性能。如图3所示，随着K 值的增大，FINFLO 算法在所有规模的数据集上的准确率也会增大，但是同时需要注意的是算法的执行时间也会随着K 值的增大相应地延长。这是所有KNN 相关算法都会遇到的问题，根据FINFLO 算法的定义我们可以知道，随着K 值的增大，数据对象的k-邻近距离会变大，在数据对象的k-近邻中包含的数据对象数量也会增大，相应的数据对象的反向k-近邻数量也会增大且k-近邻和反向k-近邻不是对称的，那么对象的邻居查找和局部异常因子计算的时间就会延长。因此在设置K 值的时候，需要综合考虑机器的性能和数据规模以及对结果精确度的要求以获得最适合的结果。

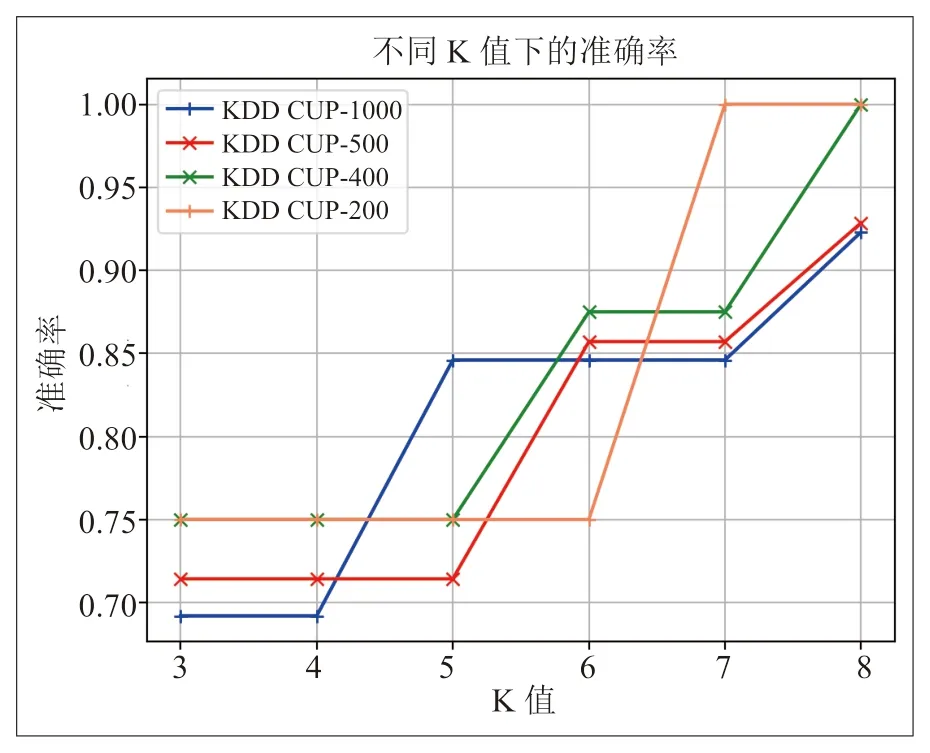
图3 FINFLO 算法在不同K 值下的准确率Fig.3 Accuracy of FINFLO algorithm under different K values

同时我们还针对三种算法设计实验，在固定K值为5，数据维度为20 的情况下测试不同数量的数据集运行时间，通过图4 我们可以看出，随着数据量的增加，三种算法的运行时间都会增长。

图4 三种算法在不同数目数据点下的运行时间对比图Fig.4 Comparison of runtime of three algorithms under different data points

4 结论与展望

离群点检测是知识发现中的一个活跃领域，相关技术被广泛应用在各种领域，在这些应用领域中研究离群点的异常行为能发现隐藏在数据集中有价值的知识。本文提出的一种基于局部密度的异常点检测算法——FINFLO 算法，该算法在计算对象的局部异常因子之前会首先计算它的反向k-近邻对象数量和所有对象反向k-近邻均值之间的关系，然后确定是否要引入反向k-近邻，这大大缩短了算法的运行时间。通过实验证明，该算法能够提高离群点检测的精度，降低时间复杂度，实现有效的局部离群点的检测。科技网后台网管系统正在迈向自动化运维，该算法结合滑动窗口可以应用于流式数据异常点的检测与判断，有较大的应用前景。

利益冲突声明

所有作者声明不存在利益冲突关系。