IMU/DGPS辅助航空摄影测量直接定位及其精度分析

韩建鹏，孙颖宏，张 鹏，陈亚锋，孟 长

（1.中国电子科技集团公司第二十七研究所，河南 郑州 450047）

航空摄影测量最基本的任务之一就是利用影像中同名像点的投影光线进行交会，获得对应地物点的空间坐标。为了获取正确的交会结果，必须恢复每条投影光线在摄影时刻的空间位置与方向，而其空间位置与方向是由相机的内方位元素和影像的外方位元素所决定的[1]。传统的航空摄影测量需要使用大量地面控制点，再通过空三加密求解影像的外方位元素。近年来，航测制图采用IMU/DGPS 辅助航空摄影测量技术，获取传感器的位置与姿态数据，再通过检校处理对系统误差进行校正，进而得到每张影像的外方位元素，直接用于后续测图而不使用地面控制点，基本满足了航测制图的精度要求[2-9]。本文利用无人机搭载飞思中画幅量测相机以及天宝高精度POS 设备进行航测作业，再利用检校场大量地面控制点对系统误差进行精确标定，最后利用检查点对直接地理定位的精度进行分析。

1 实验概况

航测传感器系统采用飞思相机iXU180，分辨率为10 328×7 760，像素大小为5.2 μm，像幅为53.7 mm×40.4 mm，镜头焦距为50 mm。GPS/INS 组合系统采用天宝AP20，水平定位精度为0.1 m，高程定位精度为0.2 m，俯仰、滚转测定精度为0.015°，偏航测定精度为0.035°。利用RTK 测量方法布设南方基站和天宝基站两个地面GPS 基准站，确保获取有效的基站数据。

实验区位于国内某大型室外标定场，占地面积为8 km2，南北方向为4 km，东西方向为2 km，海拔为400～550 m，属于典型的丘陵地形。在实验区南部等间隔均匀布设94 个地面永久性靶标，靶标中心控制点已知坐标的测量精度优于2 cm，靶标平均间距约为230 m，能满足1∶500 航测系统的系统检校和精度评价要求。

航空摄影测量工作于2018 年12 月20 日—21 日飞行两个架次完成，第一架次飞行数据主要用于系统误差检校，第二架次飞行数据用于直接地理定位精度分析。实验的航空摄影测量作业流程如图1 所示。

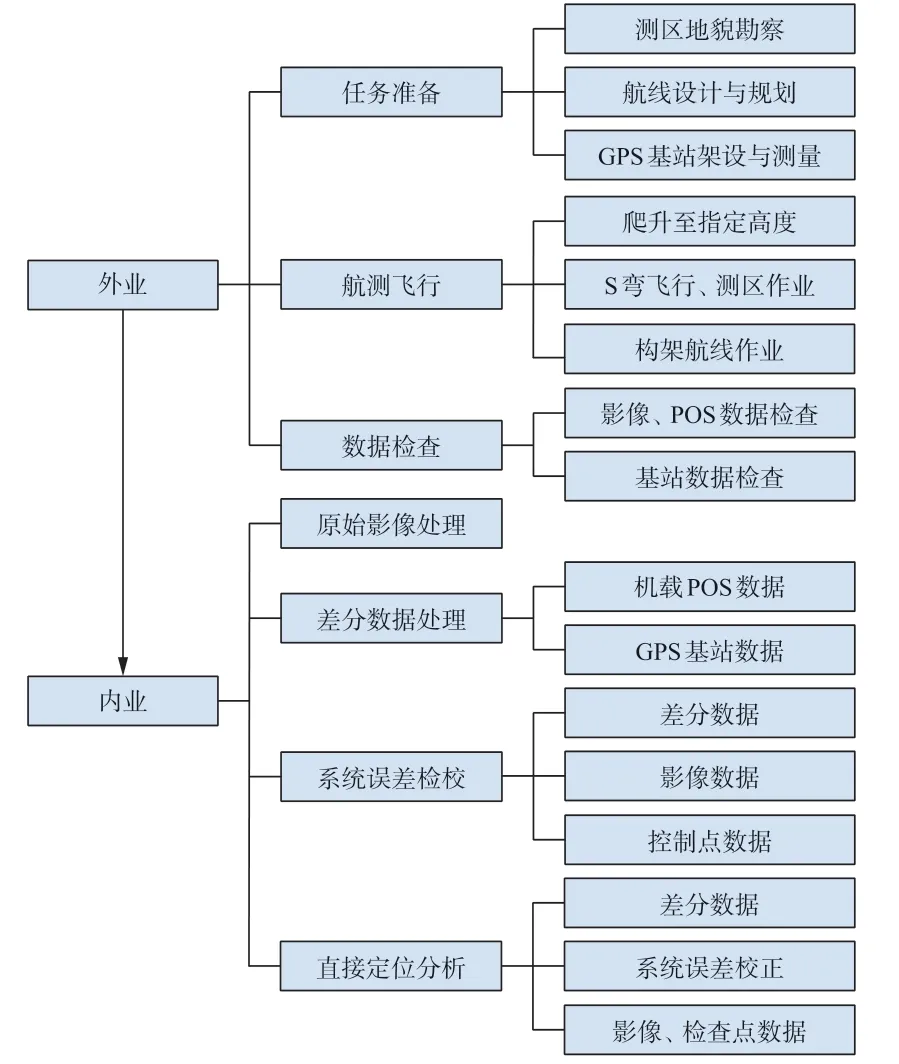
图1 航空摄影测量作业流程图

无人机起飞前带电静置5 min，以确保POS 设备完成初始化；起飞后切入航线，迅速爬升至指定高度435 m（保证最低点地面分辨率为5 cm），进行S 弯飞行，随后切入第一条航线；航向重叠度设置为70%，旁向重叠度设置为60%，共计飞行12 条航线（南北方向）；随后爬升至500 m，进行两条构架航线飞行（东西方向）；构架航线结束后无人机返航、降落，降落后带电静置5 min，以保证POS 解算精度。第二架次POS 设备记录的飞行轨迹如图2 所示，其中黄色三角形为Event 记录点（相机曝光）。第一架次获取影像及其POS 数据共259 组，第二架次获取影像及其POS数据共330 组。飞思相机采集的原始影像为其压缩格式iiq，采用影像处理软件Capture One 对影像进行格式转换，转换为jpeg 或tiff 格式，必要时可对影像进行调色处理。

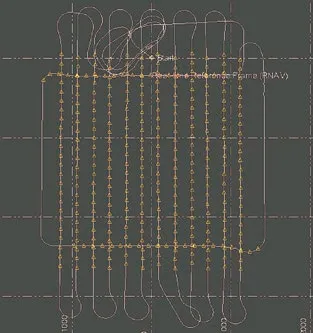
图2 第二架次POS设备记录的飞行轨迹和Event记录点

2 空中三角测量精度评估

空中三角测量是衡量航测系统测图精度的关键环节。实验采用无像控点和四角控制的方法分别进行精度评估。精度评估主要以检查点的误差为依据。

2.1 无像控点的空中三角测量精度评估

不采用地面控制点，直接进行无地面控制点的空中三角测量最能反映测绘无人机系统的整体精度。本文采用POSPac 软件对机载POS 数据、基准站数据进行事后差分解算，得到POS 设备在相机曝光中间时刻[10]（即Event）记录的经度、纬度、高度、Omega、Phi、Kappa 等参数；差分解算过程中采用CGCS2000坐标系，与基站坐标系和地面控制点坐标系保持一致。利用差分解算数据直接对第一架次（12 月20 日飞行）和第二架次（12 月21 日飞行）获取的影像进行空中三角测量，并利用测区内能清晰识别的均匀分布的全部已知靶标点作为检查点进行精度评价。统计结果如图3、4 所示。

两个架次检查点误差在X、Y、Z方向的均方根误差（RMSE）如表1 所示，可以看出，在地面控制点没有参与空中三角测量平差的情况下，基于事后差分解算数据的支持，进行光束法区域网自检校平差后，两个架次检查点X方向的RMSE 达到了4.3 cm 和3.1 cm；Y方向的RMSE 达到了3.8 cm 和5.4 cm；平面精度接近1 个像素分辨率水平；高程方向的RMSE 分别为6.7 cm 和10.4 cm，约为两个像素分辨率水平。由两个架次空中三角测量检查点位置误差来看，无像控点的情况下已完全能满足1∶500 空中三角测量的规范要求，说明整个系统精度很高、且较稳定。

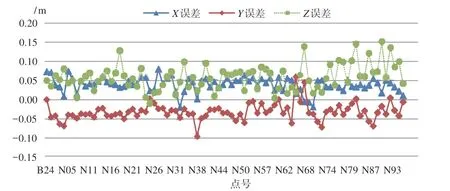
图3 第一架次无像控点情况下的地面检查点误差曲线

图4 第二架次无像控点情况下的地面检查点误差曲线

表1 无像控点情况下3 个方向检查点的RMSE

2.2 四角控制的空中三角测量精度评估

第一架次选取分布在四周的N10、N36、N62、N86 共4 个点作为控制点，其余80 个点作为检查点；第二架次选取分布在四周的B9、B12、N62、N86 共4 个点作为控制点，其余89 个点作为检查点，空中三角测量结果如表2 所示，可以看出，四角控制后空中三角测量检查点的精度有进一步提升，均达到5 cm 以内，特别是高程精度提高较多。

表2 四角控制情况下的检查点的RMSE

3 直接定位精度分析

3.1 系统误差检校

本文将第一架次所采集的机载数据（影像数据和POS 数据）、基准站数据结合大量地面点数据进行系统误差检校。利用大量地面控制点数据进行空三反算得到259 张影像姿态，与差分解算得到的姿态（经坐标系转换后）直接进行比对，结果如图5 所示，可以看出，差分解算得到的姿态有明显的系统误差，Yaw 方向误差约为0.9°，Pitch 方向误差约为0°，Roll 方向误差约为0.2°。

图5 空三反算与差分解算的影像姿态误差曲线

根据该架次实验获取的影像数据、差分解算数据、检校场84 个地面控制点数据，利用自检校光束平差法，对相机畸变参数、偏心角和偏心距进行标定，结果如表3、4 所示。

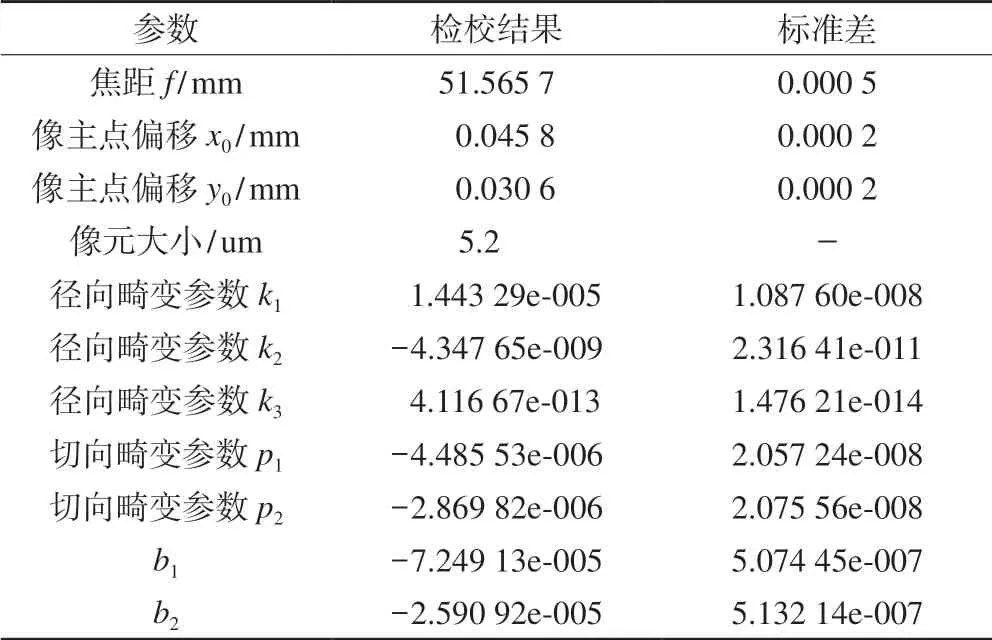
表3 相机畸变检校结果

表4 偏心角和偏心距检校结果

利用解算得到的系统误差进行自检校，将空三反算的影像姿态与差分解算姿态的检校值进行比对，如图6 所示，可以看出，系统误差已基本消除。

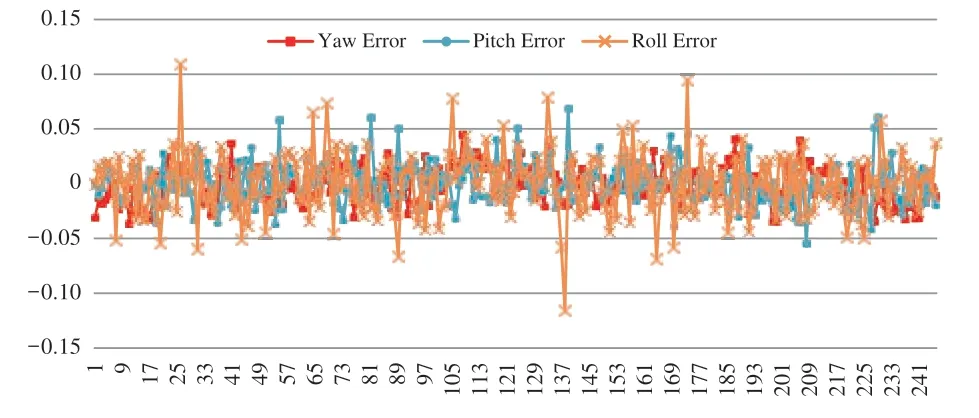
图6 系统误差自检校后的姿态误差曲线

3.2 定位精度分析

本文以第一架次的检校结果作为第二架次飞行数据的先验参数进行无地面控制点的直接地理定位，并利用地面检查点进行精度评价，同时验证检校结果的有效性。

利用第一架次检校得到的相机畸变参数、偏心角、偏心距等对第二架次数据进行固定参数（不进行自检校）空中三角测量后，将空三反算的330 张影像姿态角与差分解算得到的姿态检校值进行比对，结果如图7所示，可以看出，姿态误差已大大减小。

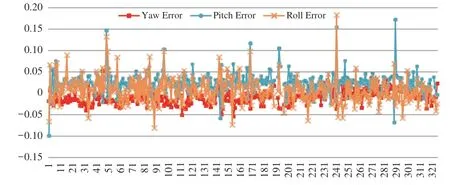
图7 第二架次系统误差检校后的姿态误差曲线

利用第一架次检校结果对第二架次的飞行数据进行无控直接定位，观察精度能否提高，是检验检校参数正确性的有效方法。本文以12 月20 日的检校结果作为12 月21 日飞行数据的先验参数进行无控空中三角测量实验，无控直接地理定位形成的DEM 如图8 所示，93 个检查点的精度如图9 所示。利用检校参数对第二架次无控直接定位的精度中误差如表5 所示，可以看出，利用检校参数后空中三角测量无控直接定位精度明显提高，特别是在高程方向，中误差由原来的10.4 cm 提高到2.6 cm，达到1 个像元分辨率以内的水平，这也说明检校参数是可靠有效的。

图8 利用检校参数对第二架次无控直接定位形成的DEM

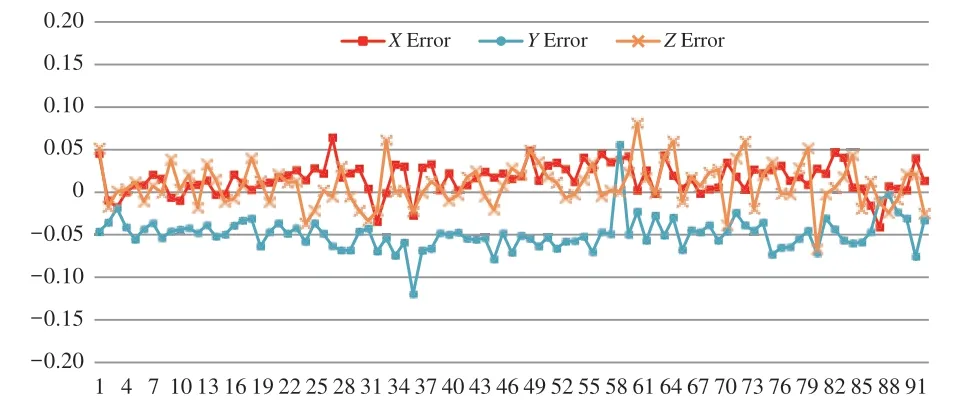
图9 利用检校参数对第二架次无控直接定位的精度曲线

表5 利用检校参数对第二架次无控直接定位的精度中误差

4 结 语

1）航测系统达到了1∶500 免像控的能力，无人机平台搭载飞思相机和POS 系统进行航测作业，POS系统解算的相机曝光时刻的位置姿态具有很高的精度。在无控情况下，多架次的检查点中误差均小于两个像素分辨率，即无需任何地面控制点，已能满足1∶500空三解算的要求。在少量（4 个）地面控制点的控制下，高程精度将得到进一步提高。

2）利用检校场均匀分布的大量地面控制点数据对相机畸变参数、偏心误差进行精确标定，并将检校参数作为另一架次飞行数据的固定参数值进行空中三角测量解算，在不再进行自检校的情况下，能明显提高另一架次的空中三角测量检查点精度，特别是高程精度。实验证明检校结果可靠有效，利用检校参数可有效提高免像控的航测精度。