基于修正JC模型和BP-ANN算法预测HNi55-7-4-2合金高温流变行为的对比

马 斌，李 平，梁 强

(重庆工商大学机械工程学院, 制造装备机构设计与控制重庆市重点实验室，重庆 400067)

0 引 言

黄铜合金具有良好的塑性成形性能、耐腐蚀性能、加工性能以及较高的强度，可制成各种形状和尺寸的铸件、锻件，广泛应用于现代机械、电气、仪表、飞机、船舶、车辆等领域[1]。HNi55-7-4-2合金是一种复杂黄铜合金，主要用于生产轿车同步器齿环；目前大部分乘用车铜质同步器齿环均采用热模锻成形。由于齿环外形结构具有薄壁、多齿的特点，其在精密锻造成形过程中容易出现金属充不满、折叠、裂纹等缺陷。目前，通常运用有限元软件模拟分析齿环热模锻成形缺陷形成的原因，而构建材料本构模型是数值模拟的重要基础，建立准确的材料模型可提高有限元模拟分析的准确性。目前，材料本构模型可分为唯象模型、物理模型和人工智能模型三大类[2]，其中唯象模型的应用较多，如Arrhenius模型[3-5]、Johnson-Cook[6-8]模型，而物理模型计算复杂，应用较少。近年来，人工智能模型因具有自身学习性能好、自适应强、模型精度高的特点而得到广泛研究[9-10]，其中反向传播的人工神经网络(Back Propagation Artificial Neural Network，BP-ANN)广泛应用于多参数复杂非线性模型的构建。目前，有关HNi55-7-4-2合金的研究主要集中在合金成分对力学性能的影响[11-12]、加工过程中的组织及性能演变[13]和合金的耐磨及耐腐蚀性能[14]等方面，但是对本构模型构建及高温流变行为的研究较少。为此，作者研究了HNi55-7-4-2合金在不同热变形条件下的流变力学行为，基于试验得到的真应力-真应变曲线，分别采用唯象模型中修正的Johnson-Cook(M-JC)模型和人工智能模型中BP-ANN算法构建该合金的本构模型，对比分析了这2个模型的预测精度。

1 试样制备与试验方法

试验材料为泸州长江机械有限公司生产的挤压态HNi55-7-4-2镍黄铜合金棒，其化学成分如表1所示，显微组织为基体β相+NiAlSi化合物强化相，强化相多呈块状和颗粒状分布在β相基体上，如图1所示。经车削加工制备尺寸为φ8 mm×12 mm的压缩试样，将试样以5 K·s-1的速率分别加热至873，923，973，1 023，1 073 K并保温3 min，然后将试样置于Gleeble-3500型热模拟试验机上进行压缩试验，应变速率为0.01，0.1，1，10 s-1，试验结束后取出水冷。通过热模拟试验机直接采集获得真应力、真应变数据。

表1 HNi55-7-4-2合金的化学成分(质量分数)

图1 HNi55-7-4-2合金的显微组织Fig.1 Microstructure of HNi55-7-4-2 alloy

2 试验结果与讨论

由图2可以看出，HNi55-7-4-2合金在高温压缩过程中的真应力随着变形温度的升高而降低，随着应变速率的提高而增大，表明该材料为温度负相关、应变速率正相关的材料。随着应变速率的增加，流变应力增大，这是因为位错密度随应变速率的增加不断增大，位错运动的速率也增大，从而表现为流变应力增大；同时，应变速率越大，在一定变形温度下的变形时间越短，发生再结晶软化的时间越短，这也会导致流变应力的增大[15]。随着变形温度的升高，在相同应变下，合金的流变应力呈下降的趋势，这是由于在变形量相同时，较高的温度能够促进动态再结晶晶粒的形核，再结晶软化效应更明显；同时变形温度的升高导致材料的形变激活能提高，金属原子的平均动能和扩散速率增大，使得材料发生回复及动态再结晶软化，削弱了加工硬化效果，因此流变应力降低。在10 s-1的高应变速率下，应力呈先急剧增大后在小应变区域出现一个凹陷峰，然后回升再稳定的现象，这表明该合金出现了明显的不连续屈服现象。

3 本构模型的建立

3.1 基于M-JC模型

3.1.1 模型的建立

原始JC模型单独考虑了应变硬化、应变速率硬化和温度软化效应，但未考虑这3个因素间的耦合作用，预测精度不高。因此，采用LIN等[6]修正的JC模型建立HNi55-7-4-2合金的本构模型，其表达式为

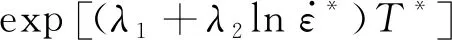
(1)

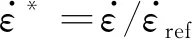
(2)

T*=T-Tref

(3)

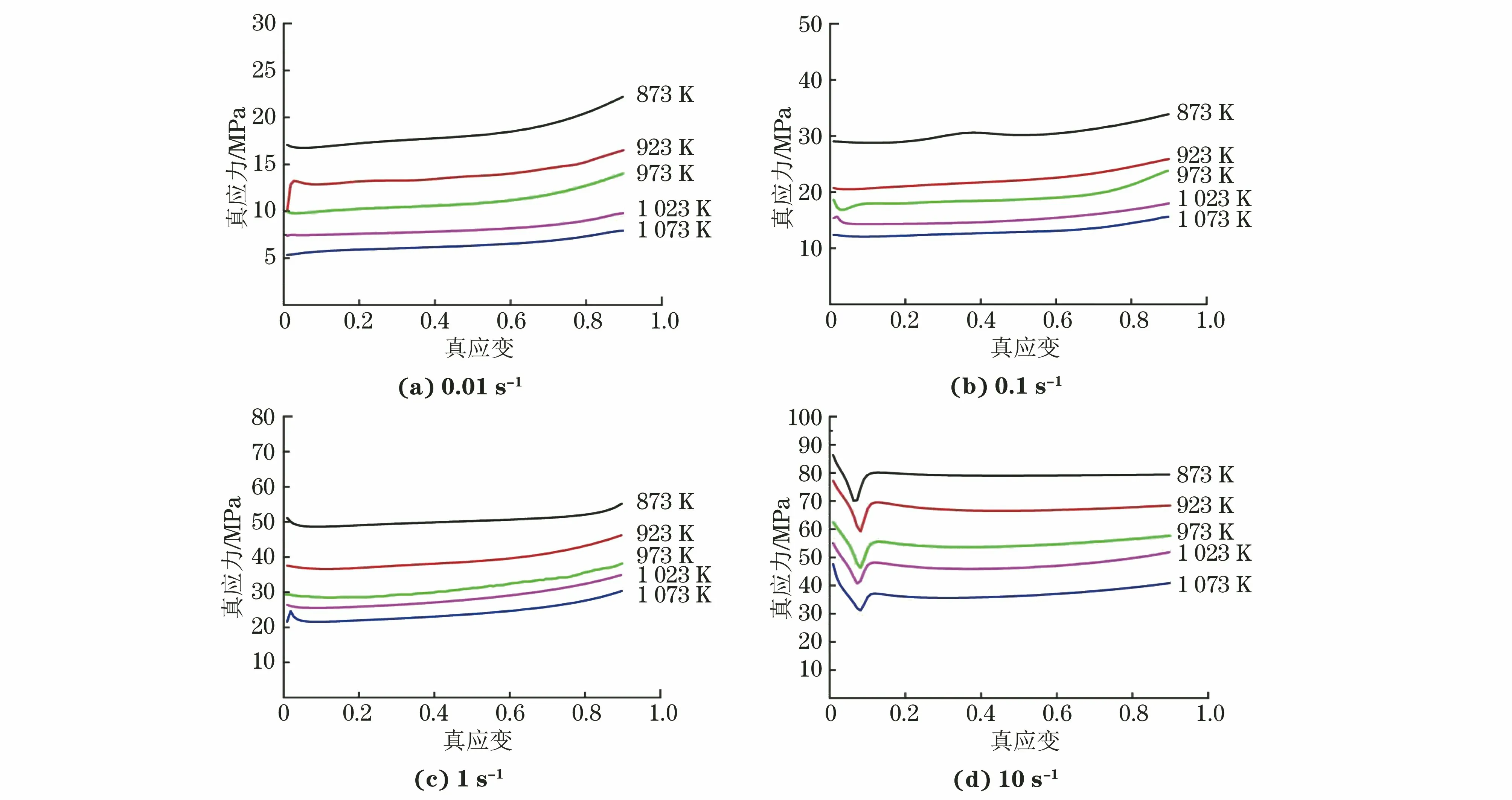
图2 HNi55-7-4-2合金在不同变形温度和应变速率下的真应力-真应变曲线Fig.2 True stress-true strain curves of HNi55-7-4-2 alloy at different deformation temperatures and strain rates

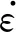
由式(1)可知，第一项(A1+B1ε+B2ε2)对拟合结果起主要作用，后两项分别为与应变速率和温度有关的调整计算项。HNi55-7-4-2合金的流变应力曲线比较复杂，为了提高预测精度，通过增加第一项多项式的阶次，即采用3阶多项式对参考条件下的应力应变数据进行拟合，修正后的模型为

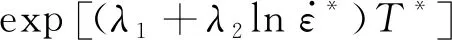
(4)

式中：B3为材料常数。

3.1.2A1,B1,B2,B3的确定

选择应变速率0.01 s-1和温度873 K作为模型求解的参考变形条件，在参考条件下式(4)可以表示为

σ=A1+B1ε+B2ε2+B3ε3

(5)

将参考应变速率和参考温度下的真应力、真应变数据绘制成散点图，采用3次多项式进行拟合，拟合结果如图3所示，根据拟合公式确定A1，B1，B2和B3的值，拟合公式为

σ=16.534+5.9024ε-13.734ε2+15.678ε3

(6)

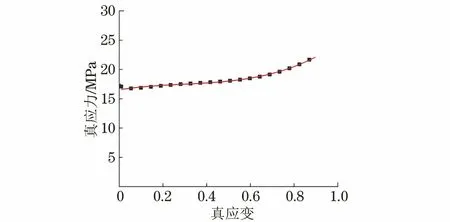
图3 在应变速率0.01 s-1、温度873 K下合金真应力与真应 变的3次多项式拟合曲线Fig.3 Cubic polynomial fitting curve of true stress and true strain of alloy at strain rate of 0.01 s-1 and temperature of 873 K

3.1.3C1的确定

在参考温度下，式(4)可以转化为

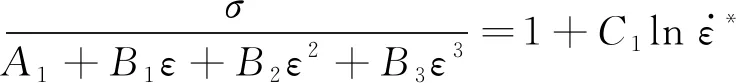
(7)

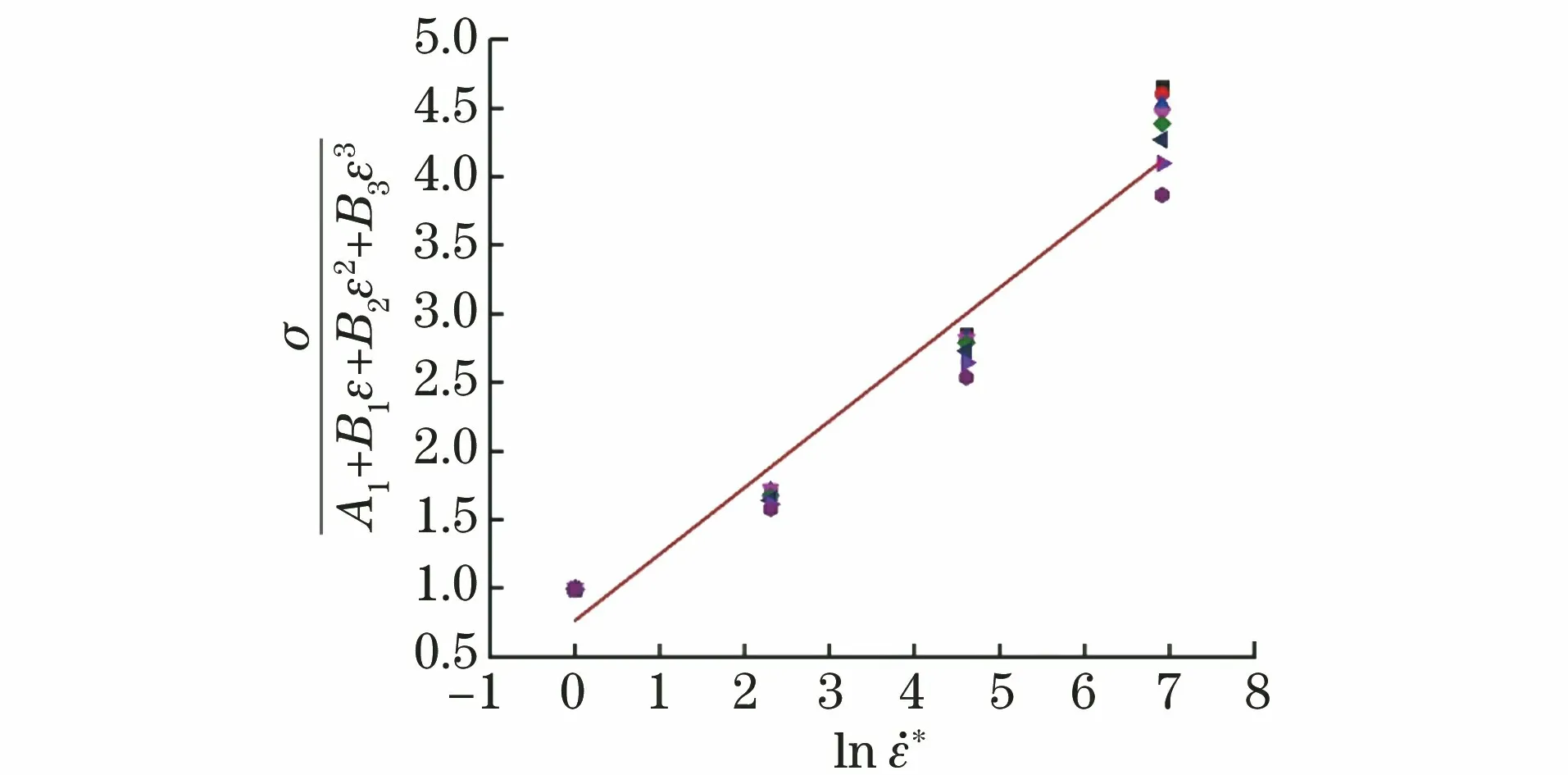
图4 在变形温度873 K、不同真应变下合金的σ/(A1+B1ε+ B2ε2+B3ε3)和的拟合曲线Fig.4 σ/(A1+B1ε+B2ε2+B3ε3) vs ln fitting curve of alloy at deformation temperature of 873 K and at different true strains

3.1.4λ1和λ2的确定

将式(4)转化为

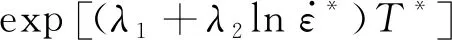
(8)

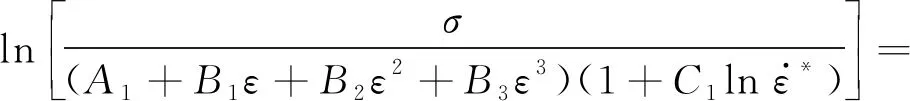
(9)

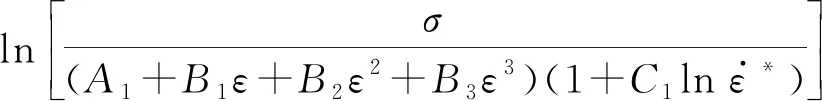
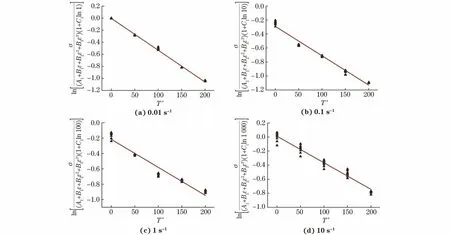
图5 不同应变速率下合金的和T*的拟合曲线Fig.5 vs T* fitting curves of alloy at different strain rates

图6 合金的拟合曲线Fig.6 λ-ln fitting curve of alloy

根据上述步骤，得到M-JC模型的参数，如表2所示。

表2 计算得到M-JC模型的参数Table 2 Parameters of M-JC model by calculation

建立的M-JC本构模型为

σ=(16.534+5.902 4ε-13.734ε2+15.678ε3)X

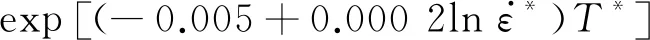
(10)

3.2 基于BP-ANN算法

由图7可见，典型的BP-ANN由输入层、隐藏层和输出层组成，输入层用于接收外部信号，输出层用于显示输出信号，隐藏层提供复杂的网状结构来模仿输入、输出信号之间的非线性关系。在隐藏层中，通过反向误差传播算法不断调整各层之间的偏差和权重，通过训练过程中的梯度下降最小化目标误差和多次迭代运算，当模型计算值与试验输入值间的误差小于设定值时，即可建立输入数据与输出数据之间的反向传播神经网络模型，从而构建出输入数据和输出数据之间的关系，再通过建立的神经网络模型预测其他输入条件下的输出值。

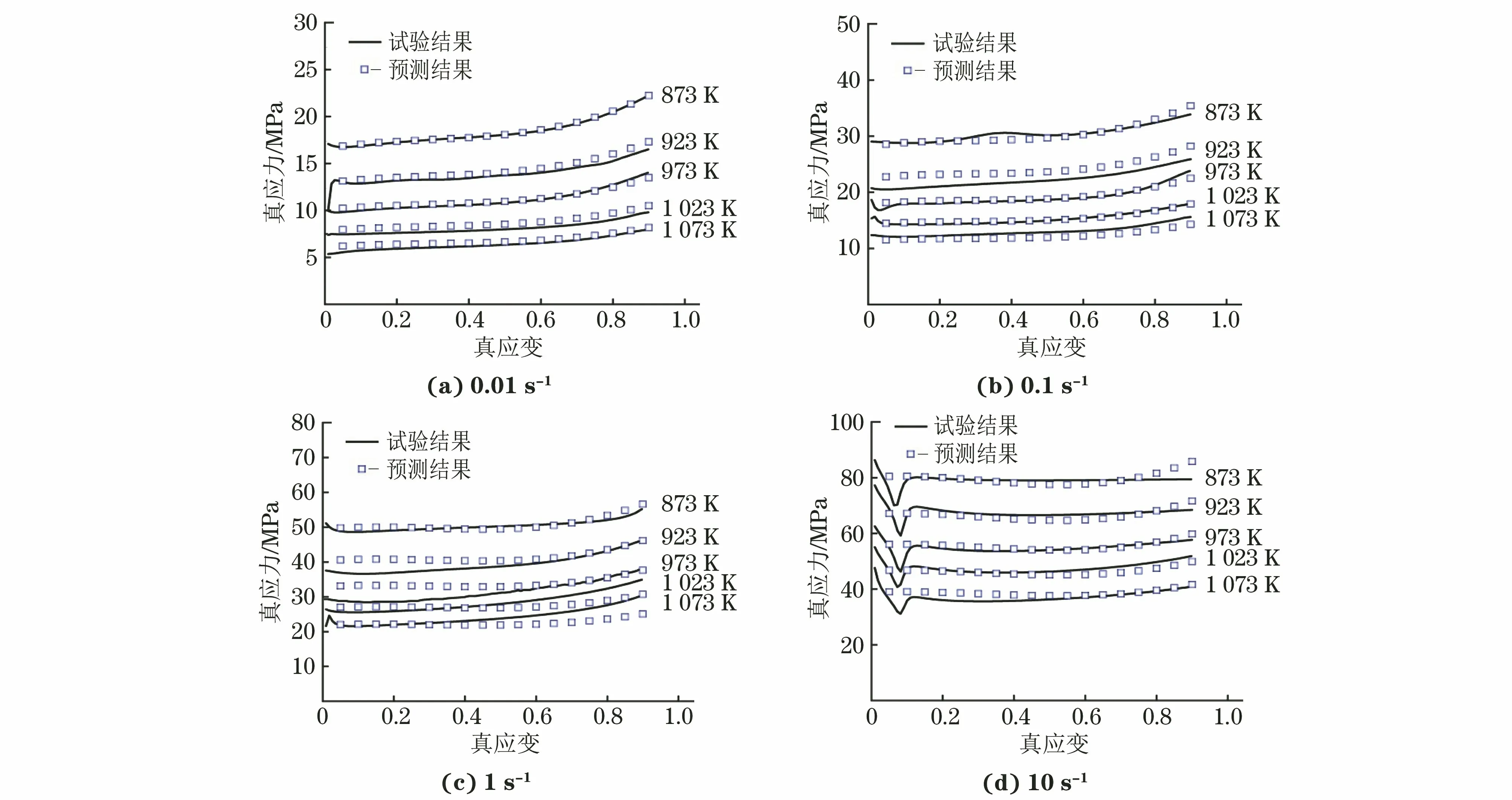
图8 基于M-JC模型预测得到不同应变速率下合金的真应力-真应变曲线与试验结果的对比Fig.8 Comparison between predicted true stress-true strain curve of alloy with M-JC model at different strain rates and experimental results

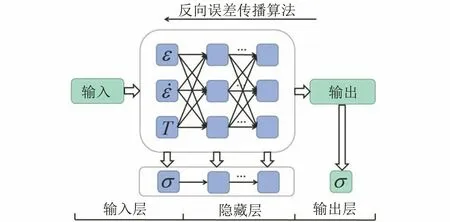
图7 BP-ANN算法原理示意Fig.7 Diagram of principal of BP-ANN algorithm

采用Matlab软件工具箱中的神经网络模型算法，建立BP-ANN结构的输入数据包括应变、应变速率、温度，输出数据为流变应力。随机选择了1 s-1、973 K变形条件下的真应力和应变数据作为测试组,用于验证模型的泛化能力，剩下19组真应力和应变数据作为训练组，设置不超过1 000次的迭代计算，对比输入的试验值与模型预测值的差异，当模型准确度达到99.5%时停止迭代，获得输入数据与输出数据之间的BP-ANN模型，保存建立的模型。为确保建模效率和准确性，训练数据的应变范围为0.05～0.90，间隔为0.01，因此共有1 634个数据作为训练数据输入。测试数据则为1 s-1、973 K变形条件下，应变范围为0.05～0.90，间隔为0.05的18个点。隐藏层每层的神经元个数为15个，隐藏层为2层，通过BP-ANN算法训练获得本构模型的结构，再运用该模型进行预测。为了提高计算效率，将所有数据进行归一化处理，采用BP-ANN算法默认的[-1,1]区间，即：

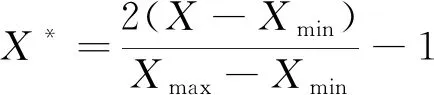
(11)

式中：X*为归一化数据；X为输入的原始数据；Xmax,Xmin为输入数据对应的最大值和最小值。

3.3 模型的准确性对比

基于M-JC模型和BP-ANN算法建的2个本构模型预测的真应力-真应变曲线如图8和图9所示。采用平均相对误差绝对值δ和相关系数R对预测精度进行评价。δ为无偏估计量，能准确反映数据的紧密程度和预测的准确性。R反映的是试验值和预测值之间线性关系的紧密性，一般该数值越大，2组数据的密切程度越高；但其为有偏估计量，样本数量带来的系统误差会影响评价的准确性。平均相对误差绝对值和相关系数的表达式分别为

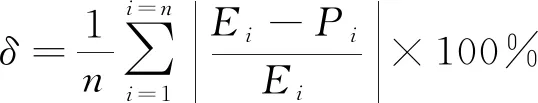
(12)

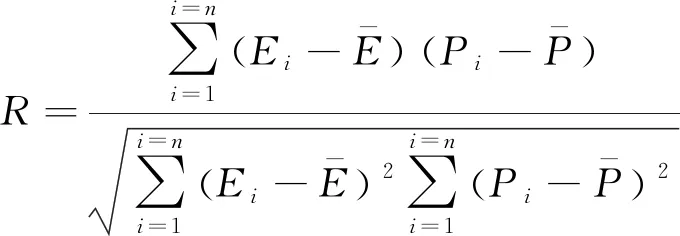
(13)

图9 基于BP-ANN算法预测得到不同应变速率下合金的真应力-真应变曲线与试验结果的对比Fig.9 Comparison between predicted true stress-true strain curve of alloy by BP-ANN algorithm at different strain rates and experimental results

式中：n为统计样本的个数；Ei和Pi分别为试验和预测的流变应力；为每组变形条件下的平均试验应力；为对应的预测平均应力。

基于M-JC本构模型预测得到的真应力与试验结果的平均相对误差绝对值为14.63%，相关系数为0.978 7，基于BP-ANN算法的平均相对误差绝对值为0.35%，相关系数为0.999 9，如图10所示。可见基于BP-ANN算法建立的本构模型的预测精度更高，试验值与预测值非常吻合，这表明BP-ANN算法可以高效准确学习应力-应变变化规律，也进一步说明了加工硬化和软化效应的关系。

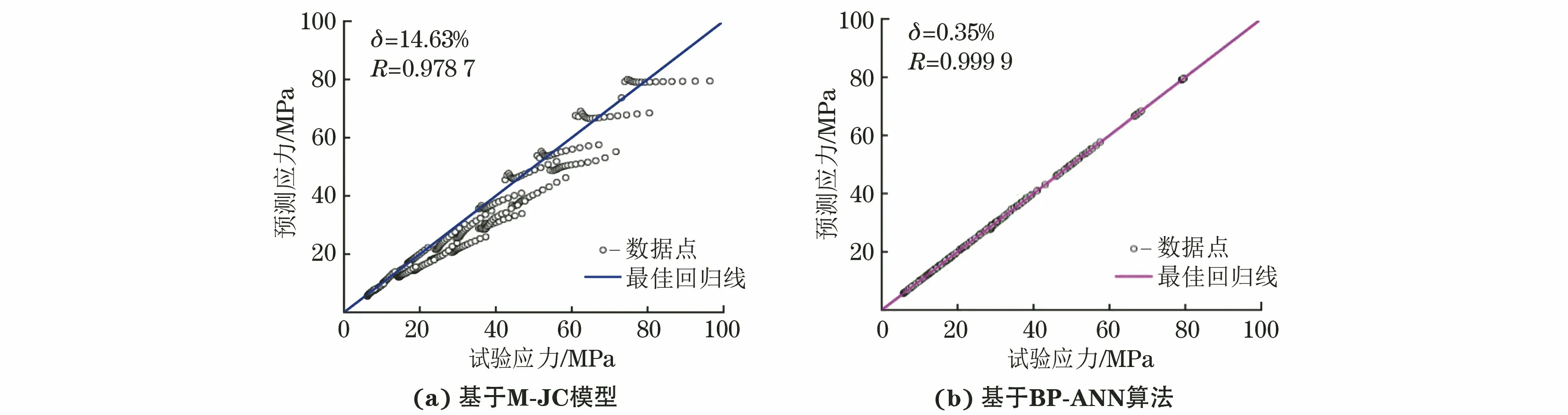
图10 基于M-JC模型与BP-ANN算法预测得到合金的真应力与试验结果之间的关系Fig.10 Relation between predicted true stress of alloy by M-JC model (a) and BP-ANN algorithm (b) and experimental results

为研究M-JC模型和BP-ANN算法的泛化能力，在随机选择的1 s-1和973 K变形条件下进行测试，采用相对误差μ和相关系数进行评估，其中相对误差的计算公式为

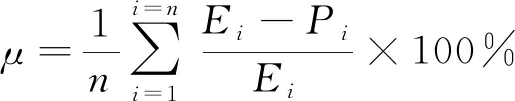
(14)

由图11可以看出：基于M-JC模型和BP-ANN算法构建的本构模型预测得的真应力与试验结果的相关系数分别为0.998 1和0.986 1，说明这2个模型的预测结果与试验结果的相关程度较高；采用基于BP-ANN算法构建的本构模型预测的真应力的相对误差仅为0.83%，远低于基于M-JC模型的相对误差(25.94%)，说明BP-ANN算法具有很好的泛化能力。

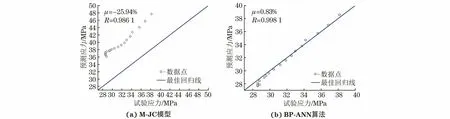
图11 应变速率1 s-1和变形温度973 K条件下基于M-JC模型与BP-ANN算法预测得到合金的真应力与试验结果之间的关系Fig.11 Relation between predicted true stress of alloy by M-JC model (a) and BP-ANN algorithm (b) and experimental results at strain rate of 1 s-1 and deformation temperature of 973 K

4 结 论

(1) HNi55-7-4-2合金为温度负相关、应变速率正相关的材料，其流变应力随着应变速率的增加而增大，随着变形温度的升高而降低，在高应变速率小应变范围内合金表现出明显的不连续屈服现象。

(2) 基于M-JC模型和BP-ANN算法建立了该合金的本构模型。基于M-JC本构模型预测得到真应力与试验结果间的平均相对误差绝对值为14.63%，相关系数为0.978 7，基于BP-ANN算法的平均相对误差绝对值为0.35%，相关系数为0.999 9；基于BP-ANN算法预测精度更高，泛化能力更好，可以较好地描述HNi55-7-4-2合金的高温流变行为。